How to calculate the frequency of a mechanical wave formula v. What is oscillation frequency? Examples of problems with solutions

Everything on the planet has its own frequency. According to one version, it even forms the basis of our world. Alas, the theory is too complex to be presented in one publication, so we will consider exclusively the frequency of oscillations as an independent action. Within the framework of the article, definitions of this physical process, its units of measurement and metrological component will be given. And finally, an example of the importance of ordinary sound in everyday life will be considered. We learn what he is and what his nature is.

What is oscillation frequency called?

By this we mean a physical quantity that is used to characterize a periodic process, which is equal to the number of repetitions or occurrences of certain events in one unit of time. This indicator is calculated as the ratio of the number of these incidents to the period of time during which they occurred. Each element of the world has its own vibration frequency. A body, an atom, a road bridge, a train, an airplane - they all make certain movements, which are called so. Even if these processes are not visible to the eye, they exist. The units of measurement in which oscillation frequency is calculated are hertz. They received their name in honor of the physicist of German origin Heinrich Hertz.

Instantaneous frequency

A periodic signal can be characterized by an instantaneous frequency, which, up to a coefficient, is the rate of phase change. It can be represented as a sum of harmonic spectral components that have their own constant oscillations.

Cyclic frequency

It is convenient to use in theoretical physics, especially in the section on electromagnetism. Cyclic frequency (also called radial, circular, angular) is a physical quantity that is used to indicate the intensity of the origin of oscillatory or rotational motion. The first is expressed in revolutions or oscillations per second. During rotational motion, the frequency is equal to the magnitude of the angular velocity vector.

This indicator is expressed in radians per second. The dimension of cyclic frequency is the reciprocal of time. In numerical terms, it is equal to the number of oscillations or revolutions that occurred in the number of seconds 2π. Its introduction for use makes it possible to significantly simplify the various range of formulas in electronics and theoretical physics. The most popular example of use is calculating the resonant cyclic frequency of an oscillatory LC circuit. Other formulas can become significantly more complex.

Discrete event rate

This value means a value that is equal to the number of discrete events that occur in one unit of time. In theory, the indicator usually used is the second minus the first power. In practice, Hertz is usually used to express the pulse frequency.

Rotation frequency

It is understood as a physical quantity that is equal to the number of full revolutions that occur in one unit of time. The indicator used here is also the second minus the first power. To indicate the work done, phrases such as revolutions per minute, hour, day, month, year and others can be used.

Units

How is oscillation frequency measured? If we take into account the SI system, then the unit of measurement here is hertz. It was originally introduced by the International Electrotechnical Commission back in 1930. And the 11th General Conference on Weights and Measures in 1960 consolidated the use of this indicator as an SI unit. What was put forward as the “ideal”? It was the frequency when one cycle is completed in one second.

But what about production? Arbitrary values ​​were assigned to them: kilocycle, megacycle per second, and so on. Therefore, when you pick up a device that operates at GHz (like a computer processor), you can roughly imagine how many actions it performs. It would seem how slowly time passes for a person. But the technology manages to perform millions and even billions of operations per second during the same period. In one hour, the computer already does so many actions that most people cannot even imagine them in numerical terms.

Metrological aspects

Oscillation frequency has found its application even in metrology. Different devices have many functions:

1. The pulse frequency is measured. They are represented by electronic counting and capacitor types.
2. The frequency of spectral components is determined. There are heterodyne and resonant types.
3. Spectrum analysis is carried out.
4. Reproduce the required frequency with a given accuracy. In this case, various measures can be used: standards, synthesizers, signal generators and other techniques in this direction.
5. The indicators of the obtained oscillations are compared; for this purpose, a comparator or oscilloscope is used.

Example of work: sound

Everything written above can be quite difficult to understand, since we used the dry language of physics. To understand the information provided, you can give an example. Everything will be described in detail, based on an analysis of cases from modern life. To do this, consider the most famous example of vibrations - sound. Its properties, as well as the features of the implementation of mechanical elastic vibrations in the medium, are directly dependent on the frequency.

The human hearing organs can detect vibrations that range from 20 Hz to 20 kHz. Moreover, with age, the upper limit will gradually decrease. If the frequency of sound vibrations drops below 20 Hz (which corresponds to the mi subcontractive), then infrasound will be created. This type, which in most cases is not audible to us, people can still feel tactilely. When the limit of 20 kilohertz is exceeded, oscillations are generated, which are called ultrasound. If the frequency exceeds 1 GHz, then in this case we will be dealing with hypersound. If we consider a musical instrument such as a piano, it can create vibrations in the range from 27.5 Hz to 4186 Hz. It should be taken into account that musical sound does not consist only of the fundamental frequency - overtones and harmonics are also mixed into it. All this together determines the timbre.

Conclusion

As you have had the opportunity to learn, vibrational frequency is an extremely important component that allows our world to function. Thanks to her, we can hear, with her assistance computers work and many other useful things are accomplished. But if the oscillation frequency exceeds the optimal limit, then certain destruction may begin. So, if you influence the processor so that its crystal operates at twice the performance, it will quickly fail.

A similar thing can be said with human life, when at high frequencies his eardrums burst. Other negative changes will also occur in the body, which will lead to certain problems, even death. Moreover, due to the peculiarities of the physical nature, this process will stretch over a fairly long period of time. By the way, taking this factor into account, the military is considering new opportunities for developing weapons of the future.

1. Mechanical waves, wave frequency. Longitudinal and transverse waves.

2. Wave front. Speed ​​and wavelength.

3. Plane wave equation.

4. Energy characteristics of the wave.

5. Some special types of waves.

6. The Doppler effect and its use in medicine.

7. Anisotropy during the propagation of surface waves. The effect of shock waves on biological tissues.

8. Basic concepts and formulas.

9. Tasks.

2.1. Mechanical waves, wave frequency. Longitudinal and transverse waves

If in any place of an elastic medium (solid, liquid or gaseous) vibrations of its particles are excited, then, due to the interaction between particles, this vibration will begin to propagate in the medium from particle to particle with a certain speed v.

For example, if an oscillating body is placed in a liquid or gaseous medium, the oscillatory motion of the body will be transmitted to the particles of the medium adjacent to it. They, in turn, involve neighboring particles in oscillatory motion, and so on. In this case, all points of the medium vibrate with the same frequency, equal to the frequency of vibration of the body. This frequency is called wave frequency.

Wave is the process of propagation of mechanical vibrations in an elastic medium.

Wave frequency is the frequency of oscillations of the points of the medium in which the wave propagates.

The wave is associated with the transfer of oscillation energy from the source of oscillations to the peripheral parts of the medium. At the same time, in the environment there arise

periodic deformations that are transferred by a wave from one point in the medium to another. The particles of the medium themselves do not move with the wave, but oscillate around their equilibrium positions. Therefore, wave propagation is not accompanied by matter transfer.

According to frequency, mechanical waves are divided into different ranges, which are listed in table. 2.1.

Table 2.1. Mechanical wave scale

Depending on the direction of particle oscillations relative to the direction of wave propagation, longitudinal and transverse waves are distinguished.

Longitudinal waves- waves, during the propagation of which the particles of the medium oscillate along the same straight line along which the wave propagates. In this case, areas of compression and rarefaction alternate in the medium.

Longitudinal mechanical waves can arise in all media (solid, liquid and gaseous).

Transverse waves- waves, during the propagation of which the particles oscillate perpendicular to the direction of propagation of the wave. In this case, periodic shear deformations occur in the medium.

In liquids and gases, elastic forces arise only during compression and do not arise during shear, therefore transverse waves are not formed in these media. The exception is waves on the surface of a liquid.

2.2. Wave front. Speed ​​and wavelength

In nature, there are no processes that propagate at an infinitely high speed, therefore, a disturbance created by an external influence at one point in the medium will not reach another point instantly, but after some time. In this case, the medium is divided into two regions: a region whose points are already involved in oscillatory motion, and a region whose points are still in equilibrium. The surface separating these areas is called wave front.

Wave front - the geometric locus of the points to which the oscillation (perturbation of the medium) has reached at this moment.

When a wave propagates, its front moves, moving at a certain speed, which is called the wave speed.

The wave speed (v) is the speed at which its front moves.

The speed of the wave depends on the properties of the medium and the type of wave: transverse and longitudinal waves in a solid body propagate at different speeds.

The speed of propagation of all types of waves is determined under the condition of weak wave attenuation by the following expression:

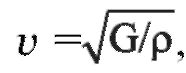where G is the effective modulus of elasticity, ρ is the density of the medium.

The speed of a wave in a medium should not be confused with the speed of movement of the particles of the medium involved in the wave process. For example, when a sound wave propagates in air, the average vibration speed of its molecules is about 10 cm/s, and the speed of a sound wave under normal conditions is about 330 m/s.

The shape of the wavefront determines the geometric type of the wave. The simplest types of waves on this basis are flat And spherical.

Flat is a wave whose front is a plane perpendicular to the direction of propagation.

Plane waves arise, for example, in a closed piston cylinder with gas when the piston oscillates.

The amplitude of the plane wave remains virtually unchanged. Its slight decrease with distance from the wave source is associated with the viscosity of the liquid or gaseous medium.

Spherical called a wave whose front has the shape of a sphere.

This, for example, is a wave caused in a liquid or gaseous medium by a pulsating spherical source.

The amplitude of a spherical wave decreases with distance from the source in inverse proportion to the square of the distance.

To describe a number of wave phenomena, such as interference and diffraction, a special characteristic called wavelength is used.

Wavelength is the distance over which its front moves in a time equal to the period of oscillation of the particles of the medium:

Here v- wave speed, T - oscillation period, ν - frequency of oscillations of points in the medium, ω - cyclic frequency.

Since the speed of wave propagation depends on the properties of the medium, the wavelength λ when moving from one environment to another changes, while the frequency ν remains the same.

This definition of wavelength has an important geometric interpretation. Let's look at Fig. 2.1 a, which shows the displacements of points in the medium at some point in time. The position of the wave front is marked by points A and B.

After a time T equal to one oscillation period, the wave front will move. Its positions are shown in Fig. 2.1, b points A 1 and B 1. From the figure it can be seen that the wavelength λ equal to the distance between adjacent points oscillating in the same phase, for example, the distance between two adjacent maxima or minima of a disturbance.

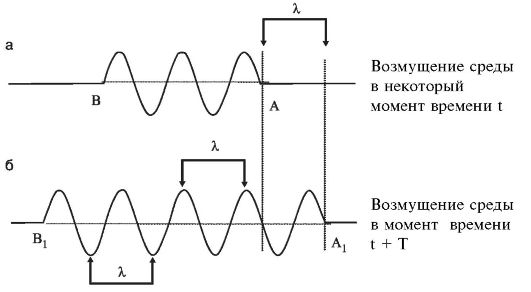Rice. 2.1. Geometric interpretation of wavelength

2.3. Plane wave equation

A wave arises as a result of periodic external influences on the environment. Consider the distribution flat wave created by harmonic oscillations of the source:

where x and is the displacement of the source, A is the amplitude of oscillations, ω is the circular frequency of oscillations.

If a certain point in the medium is distant from the source at a distance s, and the wave speed is equal to v, then the disturbance created by the source will reach this point after time τ = s/v. Therefore, the phase of oscillations at the point in question at time t will be the same as the phase of oscillations of the source at time (t - s/v), and the amplitude of the oscillations will remain practically unchanged. As a result, the oscillations of this point will be determined by the equation

Here we have used formulas for circular frequency (ω = 2π/T) and wavelength (λ = v T).

Substituting this expression into the original formula, we get

Equation (2.2), which determines the displacement of any point in the medium at any time, is called plane wave equation. The argument for cosine is magnitude φ = ωt - 2 π s /λ - called wave phase.

2.4. Energy characteristics of the wave

The medium in which the wave propagates has mechanical energy, which is the sum of the energies of the vibrational motion of all its particles. The energy of one particle with mass m 0 is found according to formula (1.21): E 0 = m 0 Α 2ω 2 /2. A unit volume of the medium contains n = p/m 0 particles (ρ - density of the medium). Therefore, a unit volume of the medium has energy w р = nЕ 0 = ρ Α 2ω 2 /2.

Volumetric energy density(\¥р) - energy of vibrational motion of particles of the medium contained in a unit of its volume:

where ρ is the density of the medium, A is the amplitude of particle oscillations, ω is the frequency of the wave.

As a wave propagates, the energy imparted by the source is transferred to distant areas.

To quantitatively describe energy transfer, the following quantities are introduced.

Energy flow(F) - a value equal to the energy transferred by a wave through a given surface per unit time:

Wave intensity or energy flux density (I) - a value equal to the energy flux transferred by a wave through a unit area perpendicular to the direction of wave propagation:

It can be shown that the intensity of a wave is equal to the product of the speed of its propagation and the volumetric energy density

2.5. Some special varieties

waves

1. Shock waves. When sound waves propagate, the speed of particle vibration does not exceed several cm/s, i.e. it is hundreds of times less than the wave speed. Under strong disturbances (explosion, movement of bodies at supersonic speed, powerful electrical discharge), the speed of oscillating particles of the medium can become comparable to the speed of sound. This creates an effect called a shock wave.

During an explosion, high-density products heated to high temperatures expand and compress a thin layer of surrounding air.

Shock wave - a thin transition region propagating at supersonic speed, in which there is an abrupt increase in pressure, density and speed of movement of matter.

The shock wave can have significant energy. Thus, during a nuclear explosion, about 50% of the total explosion energy is spent on the formation of a shock wave in the environment. The shock wave, reaching objects, can cause destruction.

2. Surface waves. Along with body waves in continuous media, in the presence of extended boundaries, there can be waves localized near the boundaries, which play the role of waveguides. These are, in particular, surface waves in liquids and elastic media, discovered by the English physicist W. Strutt (Lord Rayleigh) in the 90s of the 19th century. In the ideal case, Rayleigh waves propagate along the boundary of the half-space, decaying exponentially in the transverse direction. As a result, surface waves localize the energy of disturbances created on the surface in a relatively narrow near-surface layer.

Surface waves - waves that propagate along the free surface of a body or along the boundary of a body with other media and quickly attenuate with distance from the boundary.

An example of such waves are waves in the earth's crust (seismic waves). The penetration depth of surface waves is several wavelengths. At a depth equal to the wavelength λ, the volumetric energy density of the wave is approximately 0.05 of its volumetric density at the surface. The displacement amplitude quickly decreases with distance from the surface and practically disappears at a depth of several wavelengths.

3. Excitation waves in active media.

An actively excitable, or active, environment is a continuous environment consisting of a large number of elements, each of which has a reserve of energy.

In this case, each element can be in one of three states: 1 - excitation, 2 - refractoriness (non-excitability for a certain time after excitation), 3 - rest. Elements can become excited only from a state of rest. Excitation waves in active media are called autowaves. Autowaves - These are self-sustaining waves in an active medium, maintaining their characteristics constant due to energy sources distributed in the medium.

The characteristics of an autowave - period, wavelength, propagation speed, amplitude and shape - in a steady state depend only on the local properties of the medium and do not depend on the initial conditions. In table 2.2 shows the similarities and differences between autowaves and ordinary mechanical waves.

Autowaves can be compared with the spread of fire in the steppe. The flame spreads over an area with distributed energy reserves (dry grass). Each subsequent element (dry blade of grass) is ignited from the previous one. And thus the front of the excitation wave (flame) propagates through the active medium (dry grass). When two fires meet, the flame disappears because the energy reserves are exhausted - all the grass has burned out.

A description of the processes of propagation of autowaves in active media is used to study the propagation of action potentials along nerve and muscle fibers.

Table 2.2. Comparison of autowaves and ordinary mechanical waves

2.6. The Doppler effect and its use in medicine

Christian Doppler (1803-1853) - Austrian physicist, mathematician, astronomer, director of the world's first physical institute.

Doppler effect consists of a change in the frequency of oscillations perceived by the observer due to the relative movement of the source of oscillations and the observer.

The effect is observed in acoustics and optics.

Let us obtain a formula describing the Doppler effect for the case when the source and receiver of the wave move relative to the medium along the same straight line with velocities v I and v P, respectively. Source performs harmonic oscillations with frequency ν 0 relative to its equilibrium position. The wave created by these oscillations propagates through the medium at a speed v. Let us find out what frequency of oscillations will be recorded in this case receiver.

Disturbances created by source oscillations propagate through the medium and reach the receiver. Consider one complete oscillation of the source, which begins at time t 1 = 0

and ends at the moment t 2 = T 0 (T 0 is the period of oscillation of the source). The disturbances of the environment created at these moments of time reach the receiver at moments t" 1 and t" 2, respectively. In this case, the receiver records oscillations with a period and frequency:

Let's find the moments t" 1 and t" 2 for the case when the source and receiver are moving towards each other, and the initial distance between them is equal to S. At the moment t 2 = T 0 this distance will become equal to S - (v И + v П)T 0 (Fig. 2.2).

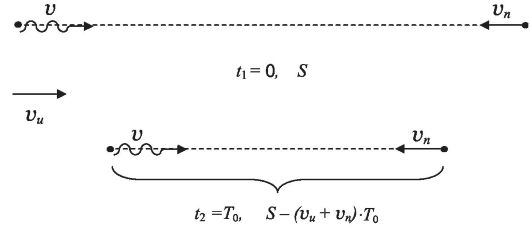Rice. 2.2. The relative position of the source and receiver at moments t 1 and t 2

This formula is valid for the case when the velocities v and and v p are directed towards each other. In general, when moving

source and receiver along one straight line, the formula for the Doppler effect takes the form

For the source, the speed v And is taken with a “+” sign if it moves in the direction of the receiver, and with a “-” sign otherwise. For the receiver - similarly (Fig. 2.3).

Rice. 2.3. Selection of signs for the speeds of the source and receiver of waves

Let's consider one special case of using the Doppler effect in medicine. Let the ultrasound generator be combined with a receiver in the form of some technical system that is stationary relative to the medium. The generator emits ultrasound with a frequency ν 0, which propagates in the medium with a speed v. Towards a certain body is moving in a system with a speed vt. First the system performs the role source (v AND= 0), and the body is the role of the receiver (v Tl= v T). The wave is then reflected from the object and recorded by a stationary receiving device. In this case v И = v T, and v p = 0.

Applying formula (2.7) twice, we obtain a formula for the frequency recorded by the system after reflection of the emitted signal:

At approaching object to the sensor frequency of the reflected signal increases, and when removal - decreases.

By measuring the Doppler frequency shift, from formula (2.8) you can find the speed of movement of the reflecting body:

The “+” sign corresponds to the movement of the body towards the emitter.

The Doppler effect is used to determine the speed of blood flow, the speed of movement of the valves and walls of the heart (Doppler echocardiography) and other organs. A diagram of the corresponding installation for measuring blood velocity is shown in Fig. 2.4.

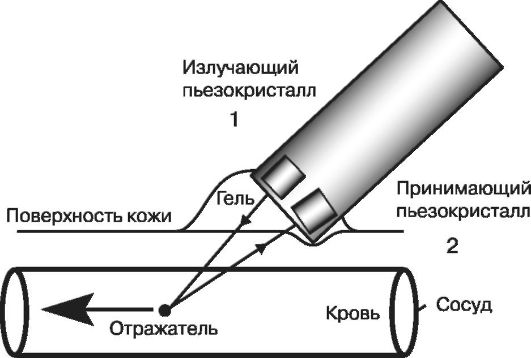Rice. 2.4. Installation diagram for measuring blood velocity: 1 - ultrasound source, 2 - ultrasound receiver

The installation consists of two piezoelectric crystals, one of which is used to generate ultrasonic vibrations (inverse piezoelectric effect), and the second is used to receive ultrasound (direct piezoelectric effect) scattered by blood.

Example. Determine the speed of blood flow in the artery if, with counter reflection of ultrasound (ν 0 = 100 kHz = 100,000 Hz, v = 1500 m/s) a Doppler frequency shift occurs from red blood cells ν D = 40 Hz.

Solution. Using formula (2.9) we find:

v 0 = v D v /2v 0 = 40x 1500/(2x 100,000) = 0.3 m/s.

2.7. Anisotropy during the propagation of surface waves. The effect of shock waves on biological tissues

1. Anisotropy of surface wave propagation. When studying the mechanical properties of the skin using surface waves at a frequency of 5-6 kHz (not to be confused with ultrasound), acoustic anisotropy of the skin appears. This is expressed in the fact that the speed of propagation of a surface wave in mutually perpendicular directions - along the vertical (Y) and horizontal (X) axes of the body - differs.

To quantify the severity of acoustic anisotropy, the mechanical anisotropy coefficient is used, which is calculated by the formula:

Where v y- speed along the vertical axis, v x- along the horizontal axis.

The anisotropy coefficient is taken as positive (K+) if v y> v x at v y < v x the coefficient is taken as negative (K -). Numerical values ​​of the speed of surface waves in the skin and the degree of anisotropy are objective criteria for assessing various effects, including on the skin.

2. The effect of shock waves on biological tissues. In many cases of impact on biological tissues (organs), it is necessary to take into account the resulting shock waves.

For example, a shock wave occurs when a blunt object hits the head. Therefore, when designing protective helmets, care is taken to absorb the shock wave and protect the back of the head in the event of a frontal impact. This purpose is served by the inner tape in the helmet, which at first glance seems necessary only for ventilation.

Shock waves occur in tissues when they are exposed to high-intensity laser radiation. Often after this, scar (or other) changes begin to develop in the skin. This, for example, occurs in cosmetic procedures. Therefore, in order to reduce the harmful effects of shock waves, it is necessary to calculate the dosage of exposure in advance, taking into account the physical properties of both the radiation and the skin itself.

Rice. 2.5. Propagation of radial shock waves

Shock waves are used in radial shock wave therapy. In Fig. Figure 2.5 shows the propagation of radial shock waves from the applicator.

Such waves are created in devices equipped with a special compressor. The radial shock wave is generated by a pneumatic method. The piston located in the manipulator moves at high speed under the influence of a controlled pulse of compressed air. When the piston strikes the applicator mounted in the manipulator, its kinetic energy is converted into mechanical energy of the area of ​​the body that was impacted. In this case, to reduce losses during transmission of waves in the air gap located between the applicator and the skin, and to ensure good conductivity of shock waves, a contact gel is used. Normal operating mode: frequency 6-10 Hz, operating pressure 250 kPa, number of pulses per session - up to 2000.

1. On the ship, a siren is turned on, signaling in the fog, and after t = 6.6 s an echo is heard. How far away is the reflective surface? Speed ​​of sound in air v= 330 m/s.

Solution

In time t, sound travels a distance of 2S: 2S = vt →S = vt/2 = 1090 m. Answer: S = 1090 m.

2. What is the minimum size of objects that bats can detect using their 100,000 Hz sensor? What is the minimum size of objects that dolphins can detect using a frequency of 100,000 Hz?

Solution

The minimum dimensions of an object are equal to the wavelength:

λ 1= 330 m/s / 10 5 Hz = 3.3 mm. This is approximately the size of the insects that bats feed on;

λ 2= 1500 m/s / 10 5 Hz = 1.5 cm. A dolphin can detect a small fish.

Answer:λ 1= 3.3 mm; λ 2= 1.5 cm.

3. First, a person sees a flash of lightning, and 8 seconds later he hears a clap of thunder. At what distance from him did the lightning flash?

Solution

S = v star t = 330 x 8 = 2640 m. Answer: 2640 m.

4. Two sound waves have the same characteristics, except that one has twice the wavelength of the other. Which one carries more energy? How many times?

Solution

The intensity of the wave is directly proportional to the square of the frequency (2.6) and inversely proportional to the square of the wavelength (ω = 2πv/λ ). Answer: the one with the shorter wavelength; 4 times.

5. A sound wave with a frequency of 262 Hz travels through air at a speed of 345 m/s. a) What is its wavelength? b) How long does it take for the phase at a given point in space to change by 90°? c) What is the phase difference (in degrees) between points 6.4 cm apart?

Solution

A) λ = v /ν = 345/262 = 1.32 m;

V) Δφ = 360°s/λ= 360 x 0.064/1.32 = 17.5°. Answer: A) λ = 1.32 m; b) t = T/4; V) Δφ = 17.5°.

6. Estimate the upper limit (frequency) of ultrasound in air if its propagation speed is known v= 330 m/s. Assume that air molecules have a size of the order of d = 10 -10 m.

Solution

In air, a mechanical wave is longitudinal and the wavelength corresponds to the distance between the two nearest concentrations (or rarefactions) of molecules. Since the distance between the condensations cannot in any way be less than the size of the molecules, then d = λ. From these considerations we have ν = v /λ = 3,3x 10 12 Hz. Answer:ν = 3,3x 10 12 Hz.

7. Two cars are moving towards each other with speeds v 1 = 20 m/s and v 2 = 10 m/s. The first machine emits a signal with a frequency ν 0 = 800 Hz. Sound speed v= 340 m/s. What frequency signal will the driver of the second car hear: a) before the cars meet; b) after the cars meet?

8. As a train passes by, you hear the frequency of its whistle change from ν 1 = 1000 Hz (as it approaches) to ν 2 = 800 Hz (as the train moves away). What is the speed of the train?

Solution

This problem differs from the previous ones in that we do not know the speed of the sound source - the train - and the frequency of its signal ν 0 is unknown. Therefore, we obtain a system of equations with two unknowns:

Solution

Let v- wind speed, and it blows from a person (receiver) to the sound source. They are stationary relative to the ground, but relative to the air they both move to the right with speed u.

Using formula (2.7) we obtain the sound frequency. perceived by a person. It is unchanged:

Answer: the frequency will not change.

Any periodically repeating movement is called oscillatory. Therefore, the dependences of the coordinates and speed of a body on time during oscillations are described by periodic functions of time. In the school physics course, vibrations are considered in which the dependencies and velocities of the body are trigonometric functions , or a combination thereof, where is a certain number. Such oscillations are called harmonic (functions And often called harmonic functions). To solve problems on oscillations included in the program of the unified state exam in physics, you need to know the definitions of the main characteristics of oscillatory motion: amplitude, period, frequency, circular (or cyclic) frequency and phase of oscillations. Let us give these definitions and connect the listed quantities with the parameters of the dependence of the body coordinates on time, which in the case of harmonic oscillations can always be represented in the form

where , and are some numbers.

The amplitude of oscillations is the maximum deviation of an oscillating body from its equilibrium position. Since the maximum and minimum values ​​of the cosine in (11.1) are equal to ±1, the amplitude of oscillations of the body oscillating (11.1) is equal to . The period of oscillation is the minimum time after which the movement of a body is repeated. For dependence (11.1), the period can be set from the following considerations. Cosine is a periodic function with period. Therefore, the movement is completely repeated through such a value that . From here we get

The circular (or cyclic) frequency of oscillations is the number of oscillations performed per unit of time. From formula (11.3) we conclude that the circular frequency is the quantity from formula (11.1).

The oscillation phase is the argument of a trigonometric function that describes the dependence of the coordinate on time. From formula (11.1) we see that the phase of oscillations of the body, the movement of which is described by dependence (11.1), is equal to . The value of the oscillation phase at time = 0 is called the initial phase. For dependence (11.1), the initial phase of oscillations is equal to . Obviously, the initial phase of oscillations depends on the choice of the time reference point (moment = 0), which is always conditional. By changing the origin of time, the initial phase of oscillations can always be “made” equal to zero, and the sine in formula (11.1) can be “turned” into a cosine or vice versa.

The program of the unified state exam also includes knowledge of formulas for the frequency of oscillations of spring and mathematical pendulums. A spring pendulum is usually called a body that can oscillate on a smooth horizontal surface under the action of a spring, the second end of which is fixed (left figure). A mathematical pendulum is a massive body, the dimensions of which can be neglected, oscillating on a long, weightless and inextensible thread (right figure). The name of this system, “mathematical pendulum,” is due to the fact that it represents an abstract mathematical model of real ( physical) pendulum. It is necessary to remember the formulas for the period (or frequency) of oscillations of spring and mathematical pendulums. For a spring pendulum

where is the length of the thread, is the acceleration of gravity. Let's consider the application of these definitions and laws using the example of problem solving.

To find the cyclic frequency of oscillations of the load in task 11.1.1 Let's first find the period of oscillation, and then use formula (11.2). Since 10 m 28 s is 628 s, and during this time the load oscillates 100 times, the period of oscillation of the load is 6.28 s. Therefore, the cyclic frequency of oscillations is 1 s -1 (answer 2 ). IN problem 11.1.2 the load made 60 oscillations in 600 s, so the oscillation frequency is 0.1 s -1 (answer 1 ).

To understand the distance the load will travel in 2.5 periods ( problem 11.1.3), let's follow his movement. After a period, the load will return back to the point of maximum deflection, completing a complete oscillation. Therefore, during this time, the load will travel a distance equal to four amplitudes: to the equilibrium position - one amplitude, from the equilibrium position to the point of maximum deviation in the other direction - the second, back to the equilibrium position - the third, from the equilibrium position to the starting point - the fourth. During the second period, the load will again go through four amplitudes, and during the remaining half of the period - two amplitudes. Therefore, the distance traveled is equal to ten amplitudes (answer 4 ).

The amount of movement of the body is the distance from the starting point to the ending point. Over 2.5 periods in task 11.1.4 the body will have time to complete two full and half a full oscillation, i.e. will be at the maximum deviation, but on the other side of the equilibrium position. Therefore, the magnitude of the displacement is equal to two amplitudes (answer 3 ).

By definition, the phase of oscillation is the argument of a trigonometric function that describes the dependence of the coordinates of an oscillating body on time. Therefore the correct answer is problem 11.1.5 - 3 .

A period is the time of complete oscillation. This means that the return of a body back to the same point from which the body began to move does not mean that a period has passed: the body must return to the same point with the same speed. For example, a body, having started oscillations from an equilibrium position, will have time to deviate by a maximum amount in one direction, return back, deviate by a maximum in the other direction, and return back again. Therefore, during the period the body will have time to deviate by the maximum amount from the equilibrium position twice and return back. Consequently, the passage from the equilibrium position to the point of maximum deviation ( problem 11.1.6) the body spends a quarter of the period (answer 3 ).

Harmonic oscillations are those in which the dependence of the coordinates of the oscillating body on time is described by a trigonometric (sine or cosine) function of time. IN task 11.1.7 these are the functions and , despite the fact that the parameters included in them are designated as 2 and 2 . The function is a trigonometric function of the square of time. Therefore, vibrations of only quantities and are harmonic (answer 4 ).

During harmonic vibrations, the speed of the body changes according to the law , where is the amplitude of the speed oscillations (the time reference point is chosen so that the initial phase of the oscillations is equal to zero). From here we find the dependence of the kinetic energy of the body on time
(problem 11.1.8). Using further the well-known trigonometric formula, we obtain

From this formula it follows that the kinetic energy of a body changes during harmonic oscillations also according to the harmonic law, but with double the frequency (answer 2 ).

Behind the relationship between the kinetic energy of the load and the potential energy of the spring ( problem 11.1.9) is easy to follow from the following considerations. When the body is deflected by the maximum amount from the equilibrium position, the speed of the body is zero, and, therefore, the potential energy of the spring is greater than the kinetic energy of the load. On the contrary, when the body passes through the equilibrium position, the potential energy of the spring is zero, and therefore the kinetic energy is greater than the potential energy. Therefore, between the passage of the equilibrium position and the maximum deflection, the kinetic and potential energy are compared once. And since during a period the body passes four times from the equilibrium position to the maximum deflection or back, then during the period the kinetic energy of the load and the potential energy of the spring are compared with each other four times (answer 2 ).

Amplitude of speed fluctuations ( task 11.1.10) is easiest to find using the law of conservation of energy. At the point of maximum deflection, the energy of the oscillatory system is equal to the potential energy of the spring , where is the spring stiffness coefficient, is the vibration amplitude. When passing through the equilibrium position, the energy of the body is equal to the kinetic energy , where is the mass of the body, is the speed of the body when passing through the equilibrium position, which is the maximum speed of the body during the oscillation process and, therefore, represents the amplitude of the speed oscillations. Equating these energies, we find

(answer 4 ).

From formula (11.5) we conclude ( problem 11.2.2), that its period does not depend on the mass of a mathematical pendulum, and with an increase in length by 4 times, the period of oscillations increases by 2 times (answer 1 ).

A clock is an oscillatory process that is used to measure intervals of time ( problem 11.2.3). The words “clock is in a hurry” mean that the period of this process is less than what it should be. Therefore, to clarify the progress of these clocks, it is necessary to increase the period of the process. According to formula (11.5), to increase the period of oscillation of a mathematical pendulum, it is necessary to increase its length (answer 3 ).

To find the amplitude of oscillations in problem 11.2.4, it is necessary to represent the dependence of the body coordinates on time in the form of a single trigonometric function. For the function given in the condition, this can be done by introducing an additional angle. Multiplying and dividing this function by and using the formula for adding trigonometric functions, we get

where is the angle such that . From this formula it follows that the amplitude of body oscillations is (answer 4 ).

Harmonic oscillations are oscillations performed according to the laws of sine and cosine. The following figure shows a graph of changes in the coordinates of a point over time according to the cosine law.

picture

Oscillation amplitude

The amplitude of a harmonic vibration is the greatest value of the displacement of a body from its equilibrium position. The amplitude can take on different values. It will depend on how much we displace the body at the initial moment of time from the equilibrium position.

The amplitude is determined by the initial conditions, that is, the energy imparted to the body at the initial moment of time. Since sine and cosine can take values ​​in the range from -1 to 1, the equation must contain a factor Xm, expressing the amplitude of the oscillations. Equation of motion for harmonic vibrations:

x = Xm*cos(ω0*t).

Oscillation period

The period of oscillation is the time it takes to complete one complete oscillation. The period of oscillation is designated by the letter T. The units of measurement of the period correspond to the units of time. That is, in SI these are seconds.

Oscillation frequency is the number of oscillations performed per unit of time. The oscillation frequency is designated by the letter ν. The oscillation frequency can be expressed in terms of the oscillation period.

ν = 1/T.

Frequency units are in SI 1/sec. This unit of measurement is called Hertz. The number of oscillations in a time of 2*pi seconds will be equal to:

ω0 = 2*pi* ν = 2*pi/T.

Oscillation frequency

This quantity is called the cyclic frequency of oscillations. In some literature the name circular frequency appears. The natural frequency of an oscillatory system is the frequency of free oscillations.

The frequency of natural oscillations is calculated using the formula:

The frequency of natural vibrations depends on the properties of the material and the mass of the load. The greater the spring stiffness, the greater the frequency of its own vibrations. The greater the mass of the load, the lower the frequency of natural oscillations.

These two conclusions are obvious. The stiffer the spring, the greater the acceleration it will impart to the body when the system is thrown out of balance. The greater the mass of a body, the slower the speed of this body will change.

Free oscillation period:

T = 2*pi/ ω0 = 2*pi*√(m/k)

It is noteworthy that at small angles of deflection the period of oscillation of the body on the spring and the period of oscillation of the pendulum will not depend on the amplitude of the oscillations.

Let's write down the formulas for the period and frequency of free oscillations for a mathematical pendulum.

then the period will be equal

T = 2*pi*√(l/g).

This formula will be valid only for small deflection angles. From the formula we see that the period of oscillation increases with increasing length of the pendulum thread. The longer the length, the slower the body will vibrate.

The period of oscillation does not depend at all on the mass of the load. But it depends on the acceleration of free fall. As g decreases, the oscillation period will increase. This property is widely used in practice. For example, to measure the exact value of free acceleration.

Since linear speed uniformly changes direction, the circular motion cannot be called uniform, it is uniformly accelerated.

Angular velocity

Let's choose a point on the circle 1 . Let's build a radius. In a unit of time, the point will move to point 2 . In this case, the radius describes the angle. Angular velocity is numerically equal to the angle of rotation of the radius per unit time.

Period and frequency

Rotation period T- this is the time during which the body makes one revolution.

Rotation frequency is the number of revolutions per second.

Frequency and period are interrelated by the relationship

Relationship with angular velocity

Linear speed

Each point on the circle moves at a certain speed. This speed is called linear. The direction of the linear velocity vector always coincides with the tangent to the circle. For example, sparks from under a grinding machine move, repeating the direction of instantaneous speed.

Consider a point on a circle that makes one revolution, the time spent is the period T. The path that a point travels is the circumference.

Centripetal acceleration

When moving in a circle, the acceleration vector is always perpendicular to the velocity vector, directed towards the center of the circle.

Using the previous formulas, we can derive the following relationships

Points lying on the same straight line emanating from the center of the circle (for example, these could be points that lie on the spokes of a wheel) will have the same angular velocities, period and frequency. That is, they will rotate the same way, but with different linear speeds. The further a point is from the center, the faster it will move.

The law of addition of speeds is also valid for rotational motion. If the motion of a body or frame of reference is not uniform, then the law applies to instantaneous velocities. For example, the speed of a person walking along the edge of a rotating carousel is equal to the vector sum of the linear speed of rotation of the edge of the carousel and the speed of the person.

The Earth participates in two main rotational movements: diurnal (around its axis) and orbital (around the Sun). The period of rotation of the Earth around the Sun is 1 year or 365 days. The Earth rotates around its axis from west to east, the period of this rotation is 1 day or 24 hours. Latitude is the angle between the plane of the equator and the direction from the center of the Earth to a point on its surface.

According to Newton's second law, the cause of any acceleration is force. If a moving body experiences centripetal acceleration, then the nature of the forces that cause this acceleration may be different. For example, if a body moves in a circle on a rope tied to it, then the acting force is the elastic force.

If a body lying on a disk rotates with the disk around its axis, then such a force is the friction force. If the force stops its action, then the body will continue to move in a straight line

Consider the movement of a point on a circle from A to B. The linear speed is equal to v A And vB respectively. Acceleration is the change in speed per unit time. Let's find the difference between the vectors.