What is the vertex of a polygon. The vertex of the polygon is

Wiktionary has an entry for “summit” Apex is the highest point of something. The term apex can also mean: In topography... Wikipedia

VERTEX- (1) V. of the cone is the point of intersection of the generatrices of the cone; (2) V. of a polyhedron is the point at which neighboring edges of the polyhedron converge; (3) The B. of a polygon is the point at which two adjacent sides of the polygon meet; (4) V. parabola point... ... Big Polytechnic Encyclopedia

APEX, in mathematics, the point at which two sides of a triangle or other polygon meet, or three or more sides of a pyramid or other polyhedron intersect. The top point of a cone is also called the vertex... Scientific and technical encyclopedic dictionary

Convex hull construction using the divide and conquer algorithm for constructing a convex hull. Contents 1 Description 2 Definitions 3 Implementation ... Wikipedia

Convex hull construction using the divide and conquer algorithm for constructing a convex hull. Contents 1 Description 2 Definitions 3 Implementation 4 Complexity of the algorithm ... Wikipedia

Checking whether a given point belongs to a given polygon. A polygon and a point are given on a plane. A polygon can be either convex or non-convex. It is necessary to solve the question of whether a point belongs to a polygon. Thanks to the fact that... ... Wikipedia

A portion of space bounded by a collection of a finite number of planar polygons (see GEOMETRY) connected in such a way that each side of any polygon is a side of exactly one other polygon (called... ... Collier's Encyclopedia

Discrete group of holomorphic transformations of an (open) circle on the Riemann sphere, i.e., a circle or half-plane on the complex plane. Most often, the upper half-plane or the unit circle is taken as K. In the first case, the elements of the functional group are ... Mathematical Encyclopedia

To the question what is a polygon asked by the author European the best answer is

Flat closed broken line;


Types of polygons
A polygon with three vertices is called a triangle, with four - a quadrilateral, with five - a pentagon, etc.
A polygon with n vertices is called an n-gon.
A flat polygon is a figure that consists of a polygon and a finite part of the area limited by it.
A polygon is called convex if one of the following (equivalent) conditions is met:
it lies on one side of any straight line connecting its neighboring vertices. (that is, the extensions of the sides of the polygon do not intersect its other sides);
it is the intersection (that is, the common part) of several half-planes;
Each diagonal lies inside the polygon;
any segment with ends at points belonging to the polygon belongs entirely to it.
A convex polygon is called regular if all sides are equal and all angles are equal, for example, an equilateral triangle, a square and a regular pentagon.
A regular polygon with self-intersections is called a star polygon, for example, regular five-pointed and eight-pointed stars.
A convex polygon is said to be inscribed in a circle if all its vertices lie on the same circle.
A convex polygon is said to be circumscribed about a circle if all its sides touch some circle.
The vertices of a polygon are called adjacent if they are the ends of one of its sides.
The segments connecting non-adjacent vertices of a polygon are called diagonals.
The angle (or interior angle) of a polygon at a given vertex is the angle formed by its sides converging at this vertex and located in the interior region of the polygon. In particular, the angle can exceed 180° if the polygon is non-convex.
The exterior angle of a convex polygon at a given vertex is the angle adjacent to the interior angle of the polygon at this vertex. In general, an external angle is the difference between 180° and an internal angle; it can take values ​​from -180° to 180°.

Answer from Microscope[guru]
A polygon is a geometric figure, usually defined as a closed broken line.

There are three different options for defining a polygon:
Flat closed broken line;
A flat closed broken line without self-intersections;
Part of a plane bounded by a closed polyline.

In any case, the vertices of the polygon are called the vertices of the polygon, and the segments are called the sides of the polygon.

Answer from Vladislav Borovik[newbie]
A polygon is a figure that has several sides and angles.

Answer from Marriage[newbie]
a multi-gon is where there are many angles

Answer from Sasha Safenrider[newbie]
a multi-angle is where there are many angles

The concept of a polygon. What is a polygon

Polygon is a geometric figure that is a closed broken line.

There are three options for defining polygons:

• A polygon is a flat closed broken line;
• A polygon is a flat closed broken line without self-intersections;
• A polygon is a part of a plane that is bounded by a closed polyline.

The vertices of the broken line are called vertices of the polygon, and the segments - sides of the polygon.

Peaks polygons are called neighboring, if they are the ends of one of its sides.

Line segments connecting non-adjacent vertices of a polygon are called diagonals.

Angle (or interior angle) of a polygon at a given vertex, the angle formed by its sides converging at this vertex and located in the interior region of the polygon is called.

External corner of a convex polygon at a given vertex the angle adjacent to the interior angle of the polygon at this vertex is called. In general, an external angle is the difference between 180° and an internal angle

A polygon is called convex, provided that one of the following conditions is true:

• A convex polygon lies on one side of any line connecting its adjacent vertices;
• A convex polygon is the intersection of several half-planes;
• Any segment with ends at points belonging to a convex polygon belongs entirely to it.

A convex polygon is called correct, if all sides are equal and all angles are equal, for example, an equilateral triangle, a square and a regular pentagon.

A convex polygon is said to be inscribed in a circle if all its vertices lie on the same circle.

A convex polygon is said to be circumscribed about a circle if all its sides touch some circle.

Classification (types) of polygons

Classification of polygons by type can be based on many properties, the most important of which are:

• number of vertices
• convex
• right
• the ability to inscribe or describe a circle

A convex polygon always lies on one side of the line that contains any of its sides. (see above)

A regular polygon has all sides and angles equal. Due to this, they have some special properties (see square).

Self-intersecting polygons can also be regular. For example, a pentagram (“five-pointed star”).

Polygons can also be distinguished in relation to the ability to fit into a polygon or describe a circle around a polygon. There may be polygons around which it is impossible to describe a circle, and also to inscribe one. At the same time, it is always possible to describe a circle around any triangle.

Polygon Properties

• The sum of the interior angles of an n-gon is (n − 2)π.
• The sum of the interior angles of a regular n-gon is 180(n − 2).
• The number of diagonals of any polygon is n(n − 3) / 2, where n is the number of sides.

Any diagonal divides into two polygons and. For and we denote the number of vertices in and respectively. A polygon is -monotonic if it does not have split or merge vertices.

APOINT - In mathematics, the point at which two sides of a triangle or other polygon meet, or three or more sides of a pyramid or other polyhedron intersect. Algorithm for a point in a polygon - Checking whether a given point belongs to a given polygon. A polygon and a point are given on a plane. A polygon can be either convex or non-convex.

DIAGONAL - (Greek, from dia through, and gonia angle). 1) a straight line connecting the vertices of two angles in a rectilinear figure that do not lie on the same straight line. Definition. A polygon is a geometric figure bounded on all sides by a closed broken line, consisting of three or more segments (links). The segments (links) of a closed broken line are called the sides of the polygon, and the common points of two segments are its vertices.

Definition. A quadrilateral is a flat geometric figure consisting of four points (the vertices of the quadrilateral) and four consecutive segments connecting them (the sides of the quadrilateral). A quadrilateral never has three vertices on the same line. A rectangle is a quadrilateral with all right angles. A polygon can be a closed broken line with self-intersections and regular star polygons.

Lines and polygons

1) β of an n-gon with a β-side or γ-side in accordance with which angle is adjacent to its left end (when viewed from the inside). If it is oriented differently than ABC, then its upper side, equal and parallel to AB, is side P, and then n is even (there are no parallel sides in a regular odd triangle).

Polygon defined by one polyline

Let us prove that from each vertex of the polygon there are at least two diagonals. But then each side of the n-gon lies in a partition triangle containing one more of its sides. Given a convex polygon, no two sides of which are parallel.

Thus, angles corresponding to different sides do not overlap. We will move a line parallel to m and look at the length of the segment cut out on it by the polygon.

Polygon fill color

The triangulation of any polygon is not unique. This can be seen from the example in the figure. A simple polygon is a figure bounded by one closed polyline whose sides do not intersect.

Set a polygon style

Any simple -vertex polygon always has a triangulation, and the number of triangles in it is independent of the triangulation itself. In the general case, in an arbitrary -gon there are only possible options for constructing diagonals. For some classes of polygons the previous estimate can be improved. For example, if the polygon is convex, then you just need to select one of its vertices and connect it to all the others except its neighbors.

Then we prove that it contains split and merge vertices. To make a polygon monotonic, you need to get rid of split and merge vertices by drawing disjoint digonals from such vertices. Let's consider a horizontal sweeping line and move it from top to bottom along the plane on which the original polygon lies. We will stop it at each vertex of the polygon.

Adding a polygon to a map

Let and be the nearest left and right edge relative to the split vertex that it currently intersects. The type of vertex stored in does not matter. Thus, to construct a diagonal for a split vertex, you need to refer to the pointer of its left edge, which currently intersects.

In the approach described above, it is required to find the intersections of the sweeping line and the left edges of the polygon. Let's create a priority queue of vertices, in which the priority will be the -coordinate of the vertex. If two vertices have the same -coordinates, the left one has higher priority. Vertices will be added at the “stops” of the sweeping line.

From here it does not intersect any of the sides at extraneous points. Since no vertices can be inside, and both ends of any previously added diagonal must lie above, the diagonal cannot intersect any of the previously added diagonals.

We will go from top to bottom along the vertices of the polygon, drawing diagonals where possible. Consequently, our polygon lies in a strip with boundaries b and c, from which we obtain that P is the vertex of the polygon furthest from the line b containing side a.

Polygon. Vertices, corners, sides and diagonals
polygon. Perimeter of a polygon.
Simple polygon. Convex polygon.
Sum of interior angles of a convex polygon.

A flat figure formed by a closed chain of segments is called polygon. Depending on the number of angles, a polygon can be a triangle, quadrilateral, pentagon, hexagon etc. Figure 17 shows the hexagon ABCDEF. Points A, B, C, D, E, F – vertices

Polygon; angles A, B, C, D, E, F – polygon angles; segments AC, AD, BE, etc. - diagonals; AB, BC, CD, DE, EF, FA – sides of a polygon; the sum of the lengths of the sides AB + BC + ... + FA is called the perimeter and is denoted p (sometimes denoted - 2p, then p is the semi-perimeter). In elementary geometry, only simple polygons are considered, the contours of which do not have self-intersections, as shown in Fig. 18. If all the diagonals lie inside the polygon, it is called convex. The hexagon in Fig. 17 is convex; the pentagon ABCDE in Fig. 19 is not convex, since its diagonal AD lies outside. The sum of the interior angles of a convex polygon is 180º (n – 2), where n is the number of angles (or sides) of the polygon.

Parallelogram. Properties and characteristics of a parallelogram.

Rectangle. Basic properties of a rectangle. Rhombus.

Square . Trapezoid. Midlines of trapezium and triangle.

A parallelogram (ABCD, Fig. 32) is a quadrilateral whose opposite sides are parallel in pairs.

Any two opposite sides of a parallelogram are called its bases, and the distance between them is called its height (BE, Fig. 32).

Properties of a parallelogram.

1. Opposite sides of a parallelogram are equal(AB = CD, AD = BC).

2. Opposite angles of a parallelogram are equal(A=C, B=D).

3. The diagonals of a parallelogram are bisected at their intersection point.(AO = OC, BO = OD).

4. The sum of the squares of the diagonals of a parallelogram is equal to the sum of the squaresits four sides:

AC² + BD² = AB² + BC² + CD² + AD².

Signs of a parallelogram.

A quadrilateral is a parallelogram if one of the following conditions is true:

1. Opposite sides are equal in pairs(AB = CD, AD = BC).

2. Opposite angles are equal in pairs(A=C, B=D).

3. Two opposite sides are equal and parallel(AB = CD, AB || CD).

4.Diagonals bisect at their intersection point(AO = OC, BO = OD).

Rectangle.

Br />
If one of the angles of a parallelogram is right, then all other angles are also right (why?). Such a parallelogram is called a rectangle (Fig. 33).

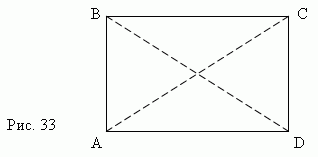
Basic properties of a rectangle.

The sides of a rectangle are also its heights.

The diagonals of the rectangle are equal: AC = BD.

The square of the diagonal of a rectangle is equal to the sum of the squares of its sides(see Pythagorean theorem above):

AC 2 = AD 2 + DC 2.

Rhombus. If all sides of a parallelogram are equal, then this parallelogram is called diamond (Fig. 34) .

The diagonals of a rhombus are mutually perpendicular (AC BD) and bisect their angles (DCA = BCA, ABD = CBD, etc.).

Square is parallelogram with right angles and equal sides (Fig. 35). A square is a special case of a rectangle and a rhombus at the same time; therefore, it has all of the above properties.

R />
Trapezoid is a quadrilateral whose opposite sides are one hundredthe rhones are parallel(Fig. 36).

Here AD || B.C. Parallel sides are called reasons trapezoid, and the other two (AB and CD) aresides.The distance between bases (BM) is height. Line segment EF connecting midpoints E and F

The lateral sides are called the midline of the trapezium. The midline of the trapezoid is equal to half the sum of the bases: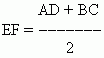

and parallel to them: EF || AD and EF || B.C.

A trapezoid with equal sides (AB = CD) is called an isosceles no trapezoid. In an equilateral trapezoid, the angles at each base are equal(A=D, B=C).

A parallelogram can be considered a special case of a trapezoid.

Middle line of the triangle- this is a segment connecting midpoints lateral sides of the triangle. The middle line of the triangle is equal to half th base and parallel to it. o property follows from the previous one

Point, since a triangle can be considered as a case of degeneration of a trapezoid, when one of its bases turns into a point.

A polygon inscribed in a circle.

A polygon circumscribed about a circle.

Described there is a circle around the polygon.

Inscribed into a polygon circle.

Radius of a circle inscribed in a triangle.

Radius of a circle circumscribed about a triangle .
Regular polygon.

Center and apothem of a regular polygon.
Ratios of sides and radii of regular polygons.

Inscribed in a circle called a polygon the vertices of which are located on the circle in Fig. 54). Described around a circle called a nogonwhose sides are tangent to the circle

(Fig. 55).

Respectively, circle passing through the vertices of a polygon(Fig.54), calleddescribed about a polygon; circle, for in which the sides of the polygon are tangent (Fig. 55), on is called inscribed in a polygon. For arbitrary it is impossible to fit a polygon into it and draw a circle around it. For triangle Nick this is always possible.

Radius r of the inscribed circleexpressed through sides a, b, c triangle:

Radius R of the described circle expressed by the formula:

A circle can be inscribed in a quadrilateral if the sums of its opposite sides are equal.For parallelograms, this is only possible for a rhombus (square). The center of the inscribed circle is located at the point of intersection of the diagonals.A circle can be described around a quadrilateral if its sumopposite angles is equal 180º. For parallelograms, this is only possible for a rectangle (square). The center of the circumscribed circle lies at the point of intersection of the diagonals. You can describe a circle around a trapezoid if it is equilateral.r />

A regular polygon is a polygon with equal sides and angles.

Fig. 56 shows a regular hexagon, and Fig. 57 shows a regular octagon. A regular quadrilateral is a square; a regular triangle is an equilateral triangle. Each angle of a regular polygon is equal to 180º (n – 2) / n, where n is the number of its angles. Inside a regular polygon there is a point O (Fig. 56), equidistant from all its vertices (OA = OB = OC = ... = OF), which is called the center of the regular polygon. The center of a regular polygon is also equidistant from all its sides (OP = OQ = OR = ...). The segments OP, OQ, OR, ... are called apothems; segments OA, OB, OC, ... are the radii of a regular polygon. A circle can be inscribed in a regular polygon and a circle can be described around it. The centers of the inscribed and circumscribed circles coincide with the center of a regular polygon. The radius of the circumcircle is the radius of a regular polygon, and the radius of the inscribed circle is its apothem. Ratios of sides and radii of regular polygons:

For most regular polygons, it is impossible to express the relationship between their sides and radii using an algebraic formula.

EXAMPLE Is it possible to cut a square with a side of 30 cm from a circle?

40 cm in diameter?

Solution: The largest square enclosed in a circle is an inscribed

Square. According to the above formula, its

Side is equal to:

Therefore, a square with a side of 30 cm cannot be cut

From a circle with a diameter of 40 cm.