Derivative of a complex function x x. Complex derivatives

Examples are given of calculating derivatives using the formula for the derivative of a complex function.

Content

See also: Proof of the formula for the derivative of a complex function

Basic formulas

Here we give examples of calculating derivatives of the following functions:
; ; ; ; .

If a function can be represented as a complex function in the following form:
,
then its derivative is determined by the formula:
.
In the examples below, we will write this formula as follows:
.
Where .
Here, the subscripts or , located under the derivative sign, denote the variables by which differentiation is performed.

Usually, in tables of derivatives, derivatives of functions from the variable x are given. However, x is a formal parameter. The variable x can be replaced by any other variable. Therefore, when differentiating a function from a variable, we simply change, in the table of derivatives, the variable x to the variable u.

Simple examples

Example 1

Find the derivative of a complex function
.

Let's write the given function in equivalent form:
.
In the table of derivatives we find:
;
.

According to the formula for the derivative of a complex function, we have:
.
Here .

Example 2

Find the derivative
.

We take the constant 5 out of the derivative sign and from the table of derivatives we find:
.

.
Here .

Example 3

Find the derivative
.

We take out a constant -1 for the sign of the derivative and from the table of derivatives we find:
;
From the table of derivatives we find:
.

We apply the formula for the derivative of a complex function:
.
Here .

More complex examples

In more complex examples, we apply the rule for differentiating a complex function several times. In this case, we calculate the derivative from the end. That is, we break the function into its component parts and find the derivatives of the simplest parts using table of derivatives. We also use rules for differentiating sums, products and fractions. Then we make substitutions and apply the formula for the derivative of a complex function.

Example 4

Find the derivative
.

Let's select the simplest part of the formula and find its derivative. .

.
Here we have used the notation
.

We find the derivative of the next part of the original function using the results obtained. We apply the rule for differentiating the sum:
.

Once again we apply the rule of differentiation of complex functions.

.
Here .

Example 5

Find the derivative of the function
.

Let's select the simplest part of the formula and find its derivative from the table of derivatives. .

We apply the rule of differentiation of complex functions.
.
Here
.

Let us differentiate the next part using the results obtained.
.
Here
.

Let's differentiate the next part.

.
Here
.

Now we find the derivative of the desired function.

.
Here
.

Basic definitions

Definition 1

A complex function is one whose argument is also a function.

It is denoted this way: f (g (x)). We have that the function g (x) is considered an argument f (g (x)).

Definition 2

If there is a function f and it is a cotangent function, then g(x) = ln x is the natural logarithm function. We find that the complex function f (g (x)) will be written as arctg(lnx). Or a function f, which is a function raised to the 4th power, where g (x) = x 2 + 2 x - 3 is considered an entire rational function, we obtain that f (g (x)) = (x 2 + 2 x - 3) 4 .

Obviously g(x) can be complex. From the example y = sin 2 x + 1 x 3 - 5 it is clear that the value of g has the cube root of the fraction. This expression can be denoted as y = f (f 1 (f 2 (x))). From where we have that f is a sine function, and f 1 is a function located under the square root, f 2 (x) = 2 x + 1 x 3 - 5 is a fractional rational function.

Definition 3

The degree of nesting is determined by any natural number and is written as y = f (f 1 (f 2 (f 3 (. . . (f n (x)))))) .

Definition 4

The concept of function composition refers to the number of nested functions according to the conditions of the problem. To solve, use the formula for finding the derivative of a complex function of the form

(f (g (x))) " = f " (g (x)) g " (x)

Examples

Example 1

Find the derivative of a complex function of the form y = (2 x + 1) 2.

Solution

The condition shows that f is a squaring function, and g(x) = 2 x + 1 is considered a linear function.

Let's apply the derivative formula for a complex function and write:

f " (g (x)) = ((g (x)) 2) " = 2 (g (x)) 2 - 1 = 2 g (x) = 2 (2 x + 1) ; g " (x) = (2 x + 1) " = (2 x) " + 1 " = 2 x " + 0 = 2 1 x 1 - 1 = 2 ⇒ (f (g (x))) " = f " (g (x)) g " (x) = 2 (2 x + 1) 2 = 8 x + 4

It is necessary to find the derivative with a simplified original form of the function. We get:

y = (2 x + 1) 2 = 4 x 2 + 4 x + 1

From here we have that

y " = (4 x 2 + 4 x + 1) " = (4 x 2) " + (4 x) " + 1 " = 4 (x 2) " + 4 (x) " + 0 = = 4 · 2 · x 2 - 1 + 4 · 1 · x 1 - 1 = 8 x + 4

The results were the same.

When solving problems of this type, it is important to understand where the function of the form f and g (x) will be located.

Example 2

You should find the derivatives of complex functions of the form y = sin 2 x and y = sin x 2.

Solution

The first function notation says that f is the squaring function and g(x) is the sine function. Then we get that

y " = (sin 2 x) " = 2 sin 2 - 1 x (sin x) " = 2 sin x cos x

The second entry shows that f is a sine function, and g(x) = x 2 denotes a power function. It follows that we write the product of a complex function as

y " = (sin x 2) " = cos (x 2) (x 2) " = cos (x 2) 2 x 2 - 1 = 2 x cos (x 2)

The formula for the derivative y = f (f 1 (f 2 (f 3 (. . . (f n (x))))) will be written as y " = f " (f 1 (f 2 (f 3 (. . . ( f n (x))))) · f 1 " (f 2 (f 3 (. . . (f n (x)))) · · f 2 " (f 3 (. . . (f n (x))) )) · . . . fn "(x)

Example 3

Find the derivative of the function y = sin (ln 3 a r c t g (2 x)).

Solution

This example shows the difficulty of writing and determining the location of functions. Then y = f (f 1 (f 2 (f 3 (f 4 (x))))) denote where f , f 1 , f 2 , f 3 , f 4 (x) is the sine function, the function of raising to 3 degree, function with logarithm and base e, arctangent and linear function.

From the formula for defining a complex function we have that

y " = f " (f 1 (f 2 (f 3 (f 4 (x)))) f 1 " (f 2 (f 3 (f 4 (x)))) f 2 " (f 3 (f 4 (x)) f 3 " (f 4 (x)) f 4 " (x)

We get what we need to find

f " (f 1 (f 2 (f 3 (f 4 (x))))) as the derivative of the sine according to the table of derivatives, then f " (f 1 (f 2 (f 3 (f 4 (x)))) ) = cos (ln 3 a r c t g (2 x)) .
f 1 " (f 2 (f 3 (f 4 (x)))) as the derivative of a power function, then f 1 " (f 2 (f 3 (f 4 (x)))) = 3 ln 3 - 1 a r c t g (2 x) = 3 ln 2 a r c t g (2 x) .
f 2 " (f 3 (f 4 (x))) as a logarithmic derivative, then f 2 " (f 3 (f 4 (x))) = 1 a r c t g (2 x) .
f 3 " (f 4 (x)) as the derivative of the arctangent, then f 3 " (f 4 (x)) = 1 1 + (2 x) 2 = 1 1 + 4 x 2.
When finding the derivative f 4 (x) = 2 x, remove 2 from the sign of the derivative using the formula for the derivative of a power function with an exponent equal to 1, then f 4 " (x) = (2 x) " = 2 x " = 2 · 1 · x 1 - 1 = 2 .

We combine the intermediate results and get that

y " = f " (f 1 (f 2 (f 3 (f 4 (x)))) f 1 " (f 2 (f 3 (f 4 (x)))) f 2 " (f 3 (f 4 (x)) f 3 " (f 4 (x)) f 4 " (x) = = cos (ln 3 a r c t g (2 x)) 3 ln 2 a r c t g (2 x) 1 a r c t g (2 x) 1 1 + 4 x 2 2 = = 6 cos (ln 3 a r c t g (2 x)) ln 2 a r c t g (2 x) a r c t g (2 x) (1 + 4 x 2)

Analysis of such functions is reminiscent of nesting dolls. Differentiation rules cannot always be applied explicitly using a derivative table. Often you need to use a formula for finding derivatives of complex functions.

There are some differences between complex appearance and complex functions. With a clear ability to distinguish this, finding derivatives will be especially easy.

Example 4

It is necessary to consider giving such an example. If there is a function of the form y = t g 2 x + 3 t g x + 1, then it can be considered as a complex function of the form g (x) = t g x, f (g) = g 2 + 3 g + 1. Obviously, it is necessary to use the formula for a complex derivative:

f " (g (x)) = (g 2 (x) + 3 g (x) + 1) " = (g 2 (x)) " + (3 g (x)) " + 1 " = = 2 · g 2 - 1 (x) + 3 g " (x) + 0 = 2 g (x) + 3 1 g 1 - 1 (x) = = 2 g (x) + 3 = 2 t g x + 3 ; g " (x) = (t g x) " = 1 cos 2 x ⇒ y " = (f (g (x))) " = f " (g (x)) g " (x) = (2 t g x + 3 ) · 1 cos 2 x = 2 t g x + 3 cos 2 x

A function of the form y = t g x 2 + 3 t g x + 1 is not considered complex, since it has the sum of t g x 2, 3 t g x and 1. However, t g x 2 is considered a complex function, then we obtain a power function of the form g (x) = x 2 and f, which is a tangent function. To do this, differentiate by amount. We get that

y " = (t g x 2 + 3 t g x + 1) " = (t g x 2) " + (3 t g x) " + 1 " = = (t g x 2) " + 3 (t g x) " + 0 = (t g x 2) " + 3 cos 2 x

Let's move on to finding the derivative of a complex function (t g x 2) ":

f " (g (x)) = (t g (g (x))) " = 1 cos 2 g (x) = 1 cos 2 (x 2) g " (x) = (x 2) " = 2 x 2 - 1 = 2 x ⇒ (t g x 2) " = f " (g (x)) g " (x) = 2 x cos 2 (x 2)

We get that y " = (t g x 2 + 3 t g x + 1) " = (t g x 2) " + 3 cos 2 x = 2 x cos 2 (x 2) + 3 cos 2 x

Functions of a complex type can be included in complex functions, and complex functions themselves can be components of functions of a complex type.

Example 5

For example, consider a complex function of the form y = log 3 x 2 + 3 cos 3 (2 x + 1) + 7 e x 2 + 3 3 + ln 2 x (x 2 + 1)

This function can be represented as y = f (g (x)), where the value of f is a function of the base 3 logarithm, and g (x) is considered the sum of two functions of the form h (x) = x 2 + 3 cos 3 (2 x + 1) + 7 e x 2 + 3 3 and k (x) = ln 2 x · (x 2 + 1) . Obviously, y = f (h (x) + k (x)).

Consider the function h(x). This is the ratio l (x) = x 2 + 3 cos 3 (2 x + 1) + 7 to m (x) = e x 2 + 3 3

We have that l (x) = x 2 + 3 cos 2 (2 x + 1) + 7 = n (x) + p (x) is the sum of two functions n (x) = x 2 + 7 and p (x) = 3 cos 3 (2 x + 1) , where p (x) = 3 p 1 (p 2 (p 3 (x))) is a complex function with numerical coefficient 3, and p 1 is a cube function, p 2 by a cosine function, p 3 (x) = 2 x + 1 by a linear function.

We found that m (x) = e x 2 + 3 3 = q (x) + r (x) is the sum of two functions q (x) = e x 2 and r (x) = 3 3, where q (x) = q 1 (q 2 (x)) is a complex function, q 1 is a function with an exponential, q 2 (x) = x 2 is a power function.

This shows that h (x) = l (x) m (x) = n (x) + p (x) q (x) + r (x) = n (x) + 3 p 1 (p 2 ( p 3 (x))) q 1 (q 2 (x)) + r (x)

When moving to an expression of the form k (x) = ln 2 x · (x 2 + 1) = s (x) · t (x), it is clear that the function is presented in the form of a complex s (x) = ln 2 x = s 1 ( s 2 (x)) with a rational integer t (x) = x 2 + 1, where s 1 is a squaring function, and s 2 (x) = ln x is logarithmic with base e.

It follows that the expression will take the form k (x) = s (x) · t (x) = s 1 (s 2 (x)) · t (x).

Then we get that

y = log 3 x 2 + 3 cos 3 (2 x + 1) + 7 e x 2 + 3 3 + ln 2 x (x 2 + 1) = = f n (x) + 3 p 1 (p 2 (p 3 (x))) q 1 (q 2 (x)) = r (x) + s 1 (s 2 (x)) t (x)

Based on the structures of the function, it became clear how and what formulas need to be used to simplify the expression when differentiating it. To become familiar with such problems and for the concept of their solution, it is necessary to turn to the point of differentiating a function, that is, finding its derivative.

If you notice an error in the text, please highlight it and press Ctrl+Enter

If g(x) And f(u) – differentiable functions of their arguments, respectively, at points x And u= g(x), then the complex function is also differentiable at the point x and is found by the formula

A typical mistake when solving derivative problems is mechanically transferring the rules for differentiating simple functions to complex functions. Let's learn to avoid this mistake.

Example 2. Find the derivative of a function

Wrong solution: calculate the natural logarithm of each term in parentheses and look for the sum of the derivatives:

Correct solution: again we determine where the “apple” is and where the “minced meat” is. Here the natural logarithm of the expression in parentheses is an “apple”, that is, a function over the intermediate argument u, and the expression in brackets is “minced meat”, that is, an intermediate argument u by independent variable x.

Then (using formula 14 from the derivatives table)

In many real-life problems, the expression with a logarithm can be somewhat more complicated, which is why there is a lesson

Example 3. Find the derivative of a function

Wrong solution:

Correct solution. Once again we determine where the “apple” is and where the “mincemeat” is. Here, the cosine of the expression in brackets (formula 7 in the table of derivatives) is an “apple”, it is prepared in mode 1, which affects only it, and the expression in brackets (the derivative of the degree is number 3 in the table of derivatives) is “minced meat”, it is prepared under mode 2, which affects only it. And as always, we connect two derivatives with the product sign. Result:

The derivative of a complex logarithmic function is a frequent task in tests, so we strongly recommend that you attend the lesson “Derivative of a logarithmic function.”

The first examples were on complex functions, in which the intermediate argument on the independent variable was a simple function. But in practical tasks it is often necessary to find the derivative of a complex function, where the intermediate argument is either itself a complex function or contains such a function. What to do in such cases? Find derivatives of such functions using tables and differentiation rules. When the derivative of the intermediate argument is found, it is simply substituted into the right place in the formula. Below are two examples of how this is done.

In addition, it is useful to know the following. If a complex function can be represented as a chain of three functions

then its derivative should be found as the product of the derivatives of each of these functions:

Many of your homework assignments may require you to open your guides in new windows. Actions with powers and roots And Operations with fractions .

Example 4. Find the derivative of a function

We apply the rule of differentiation of a complex function, not forgetting that in the resulting product of derivatives there is an intermediate argument with respect to the independent variable x does not change:

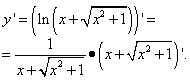
We prepare the second factor of the product and apply the rule for differentiating the sum:

The second term is the root, so

Thus, we found that the intermediate argument, which is a sum, contains a complex function as one of the terms: raising to a power is a complex function, and what is being raised to a power is an intermediate argument with respect to the independent variable x.

Therefore, we again apply the rule for differentiating a complex function:

We transform the degree of the first factor into a root, and when differentiating the second factor, do not forget that the derivative of the constant is equal to zero:

Now we can find the derivative of the intermediate argument needed to calculate the derivative of a complex function required in the problem statement y:

Example 5. Find the derivative of a function

First, we use the rule for differentiating the sum:

We obtained the sum of the derivatives of two complex functions. Let's find the first one:

Here, raising the sine to a power is a complex function, and the sine itself is an intermediate argument for the independent variable x. Therefore, we will use the rule of differentiation of a complex function, along the way taking the factor out of brackets :

Now we find the second term of the derivatives of the function y:

Here raising the cosine to a power is a complex function f, and the cosine itself is an intermediate argument in the independent variable x. Let us again use the rule for differentiating a complex function:

The result is the required derivative:

Table of derivatives of some complex functions

For complex functions, based on the rule of differentiation of a complex function, the formula for the derivative of a simple function takes a different form.

1. Derivative of a complex power function, where u x
2. Derivative of the root of the expression
3. Derivative of an exponential function
4. Special case of exponential function
5. Derivative of a logarithmic function with an arbitrary positive base A
6. Derivative of a complex logarithmic function, where u– differentiable function of the argument x
7. Derivative of sine
8. Derivative of cosine
9. Derivative of tangent
10. Derivative of cotangent
11. Derivative of arcsine
12. Derivative of arc cosine
13. Derivative of arctangent
14. Derivative of arc cotangent

Very easy to remember.

Well, let’s not go far, let’s immediately consider the inverse function. Which function is the inverse of the exponential function? Logarithm:

In our case, the base is the number:

Such a logarithm (that is, a logarithm with a base) is called “natural”, and we use a special notation for it: we write instead.

What is it equal to? Of course, .

The derivative of the natural logarithm is also very simple:

Examples:

Find the derivative of the function.
What is the derivative of the function?

Answers: The exponential and natural logarithm are uniquely simple functions from a derivative perspective. Exponential and logarithmic functions with any other base will have a different derivative, which we will analyze later, after we go through the rules of differentiation.

Rules of differentiation

Rules of what? Again a new term, again?!...

Differentiation is the process of finding the derivative.

That's all. What else can you call this process in one word? Not derivative... Mathematicians call the differential the same increment of a function at. This term comes from the Latin differentia - difference. Here.

When deriving all these rules, we will use two functions, for example, and. We will also need formulas for their increments:

There are 5 rules in total.

The constant is taken out of the derivative sign.

If - some constant number (constant), then.

Obviously, this rule also works for the difference: .

Let's prove it. Let it be, or simpler.

Examples.

Find the derivatives of the functions:

at a point;
at a point;
at a point;
at the point.

Solutions:

(the derivative is the same at all points, since it is a linear function, remember?);

Derivative of the product

Everything is similar here: let’s introduce a new function and find its increment:

Derivative:

Examples:

Find the derivatives of the functions and;
Find the derivative of the function at a point.

Solutions:

Derivative of an exponential function

Now your knowledge is enough to learn how to find the derivative of any exponential function, and not just exponents (have you forgotten what that is yet?).

So, where is some number.

We already know the derivative of the function, so let's try to reduce our function to a new base:

To do this, we will use a simple rule: . Then:

Well, it worked. Now try to find the derivative, and don't forget that this function is complex.

Happened?

Here, check yourself:

The formula turned out to be very similar to the derivative of an exponent: as it was, it remains the same, only a factor appeared, which is just a number, but not a variable.

Examples:
Find the derivatives of the functions:

Answers:

This is just a number that cannot be calculated without a calculator, that is, it cannot be written down in a simpler form. Therefore, we leave it in this form in the answer.

Note that here is the quotient of two functions, so we apply the corresponding differentiation rule:

In this example, the product of two functions:

Derivative of a logarithmic function

It’s similar here: you already know the derivative of the natural logarithm:

Therefore, to find an arbitrary logarithm with a different base, for example:

We need to reduce this logarithm to the base. How do you change the base of a logarithm? I hope you remember this formula:

Only now we will write instead:

The denominator is simply a constant (a constant number, without a variable). The derivative is obtained very simply:

Derivatives of exponential and logarithmic functions are almost never found in the Unified State Examination, but it will not be superfluous to know them.

Derivative of a complex function.

What is a "complex function"? No, this is not a logarithm, and not an arctangent. These functions can be difficult to understand (although if you find the logarithm difficult, read the topic “Logarithms” and you will be fine), but from a mathematical point of view, the word “complex” does not mean “difficult”.

Imagine a small conveyor belt: two people are sitting and doing some actions with some objects. For example, the first one wraps a chocolate bar in a wrapper, and the second one ties it with a ribbon. The result is a composite object: a chocolate bar wrapped and tied with a ribbon. To eat a chocolate bar, you need to do the reverse steps in reverse order.

Let's create a similar mathematical pipeline: first we will find the cosine of a number, and then square the resulting number. So, we are given a number (chocolate), I find its cosine (wrapper), and then you square what I got (tie it with a ribbon). What happened? Function. This is an example of a complex function: when, to find its value, we perform the first action directly with the variable, and then a second action with what resulted from the first.

In other words, a complex function is a function whose argument is another function: .

For our example, .

We can easily do the same steps in reverse order: first you square it, and I then look for the cosine of the resulting number: . It’s easy to guess that the result will almost always be different. An important feature of complex functions: when the order of actions changes, the function changes.

Second example: (same thing). .

The action we do last will be called "external" function, and the action performed first - accordingly "internal" function(these are informal names, I use them only to explain the material in simple language).

Try to determine for yourself which function is external and which internal:

Answers: Separating inner and outer functions is very similar to changing variables: for example, in a function

What action will we perform first? First, let's calculate the sine, and only then cube it. This means that it is an internal function, but an external one.
And the original function is their composition: .
Internal: ; external: .
Examination: .
Internal: ; external: .
Examination: .
Internal: ; external: .
Examination: .
Internal: ; external: .
Examination: .

We change variables and get a function.

Well, now we will extract our chocolate bar and look for the derivative. The procedure is always reversed: first we look for the derivative of the outer function, then we multiply the result by the derivative of the inner function. In relation to the original example, it looks like this:

Another example:

So, let's finally formulate the official rule:

Algorithm for finding the derivative of a complex function:

It seems simple, right?

Let's check with examples:

Solutions:

1) Internal: ;

External: ;

2) Internal: ;

(Just don’t try to cut it by now! Nothing comes out from under the cosine, remember?)

3) Internal: ;

External: ;

It is immediately clear that this is a three-level complex function: after all, this is already a complex function in itself, and we also extract the root from it, that is, we perform the third action (put the chocolate in a wrapper and with a ribbon in the briefcase). But there is no reason to be afraid: we will still “unpack” this function in the same order as usual: from the end.

That is, first we differentiate the root, then the cosine, and only then the expression in brackets. And then we multiply it all.

In such cases, it is convenient to number the actions. That is, let's imagine what we know. In what order will we perform actions to calculate the value of this expression? Let's look at an example:

The later the action is performed, the more “external” the corresponding function will be. The sequence of actions is the same as before:

Here the nesting is generally 4-level. Let's determine the course of action.

1. Radical expression. .

2. Root. .

3. Sine. .

4. Square. .

5. Putting it all together:

DERIVATIVE. BRIEFLY ABOUT THE MAIN THINGS

Derivative of a function- the ratio of the increment of the function to the increment of the argument for an infinitesimal increment of the argument:

Basic derivatives:

Rules of differentiation:

The constant is taken out of the derivative sign:

Derivative of the sum:

Derivative of the product:

Derivative of the quotient:

Derivative of a complex function:

Algorithm for finding the derivative of a complex function:

We define the “internal” function and find its derivative.
We define the “external” function and find its derivative.
We multiply the results of the first and second points.

In “old” textbooks it is also called the “chain” rule. So if y = f (u), and u = φ (x), that is

y = f (φ (x))

complex - compound function (composition of functions) then

Where , after calculation is considered at u = φ (x).

Note that here we took “different” compositions from the same functions, and the result of differentiation naturally turned out to depend on the order of “mixing”.

The chain rule naturally extends to compositions of three or more functions. In this case, there will be three or more “links” in the “chain” that makes up the derivative. Here is an analogy with multiplication: “we have” a table of derivatives; “there” - multiplication table; “with us” is the chain rule and “there” is the “column” multiplication rule. When calculating such “complex” derivatives, no auxiliary arguments (u¸v, etc.), of course, are introduced, but, having noted for themselves the number and sequence of functions involved in the composition, the corresponding links are “strung” in the indicated order.

. Here, with the “x” to obtain the value of the “y”, five operations are performed, that is, there is a composition of five functions: “external” (the last of them) - exponential - e  ; then in reverse order, power. (♦) 2 ; trigonometric sin(); sedate. () 3 and finally logarithmic ln.(). That's why

With the following examples we will “kill a couple of birds with one stone”: we will practice differentiating complex functions and add to the table of derivatives of elementary functions. So:

4. For a power function - y = x α - rewriting it using the well-known “basic logarithmic identity” - b=e ln b - in the form x α = x α ln x we obtain

5. For an arbitrary exponential function, using the same technique we will have

6. For an arbitrary logarithmic function, using the well-known formula for transition to a new base, we consistently obtain

7. To differentiate the tangent (cotangent), we use the rule for differentiating quotients:

To obtain the derivatives of inverse trigonometric functions, we use the relation that is satisfied by the derivatives of two mutually inverse functions, that is, the functions φ (x) and f (x) related by the relations:

This is the ratio

It is from this formula for mutually inverse functions

And
,

Finally, let us summarize these and some other derivatives that are also easily obtained in the following table.