Definition of a ball. Mathematics

A ball is a body consisting of all points in space that are located at a distance not greater than a given one from a given point. This point is called the center of the ball, and this distance is called the radius of the ball. The boundary of a ball is called a spherical surface or sphere. The points of the sphere are all points of the ball that are removed from the center at a distance equal to the radius. Any segment that connects the center of a ball to a point on the spherical surface is also called a radius. The segment passing through the center of the ball and connecting two points on the spherical surface is called the diameter. The ends of any diameter are called diametrically opposite points of the ball.

A ball is a body of revolution, just like a cone and a cylinder. A ball is obtained by rotating a semicircle around its diameter as an axis.

The surface area of ​​the ball can be found using the formulas:

where r is the radius of the ball, d is the diameter of the ball.

The volume of the ball is found by the formula:

V = 4 / 3 πr 3,

where r is the radius of the ball.

Theorem. Every section of a ball by a plane is a circle. The center of this circle is the base of the perpendicular drawn from the center of the ball onto the cutting plane.

Based on this theorem, if a ball with center O and radius R is intersected by the plane α, then the cross-section results in a circle of radius r with center K. The radius of the section of the ball by the plane can be found by the formula

From the formula it is clear that planes equidistant from the center intersect the ball in equal circles. The radius of the section is greater, the closer the cutting plane is to the center of the ball, that is, the smaller the distance OK. The greatest radius has a section by a plane passing through the center of the ball. The radius of this circle is equal to the radius of the ball.

The plane passing through the center of the ball is called the center plane. The section of a ball by the diametrical plane is called a great circle, and the section of a sphere is called a great circle, and the section of a sphere is called a great circle.

Theorem. Any diametrical plane of a ball is its plane of symmetry. The center of the ball is its center of symmetry.

The plane that passes through point A of the spherical surface and is perpendicular to the radius drawn to point A is called the tangent plane. Point A is called the tangent point.

Theorem. The tangent plane has only one common point with the ball - the point of contact.

The straight line that passes through point A of the spherical surface perpendicular to the radius drawn to this point is called a tangent.

Theorem. An infinite number of tangents pass through any point on the spherical surface, and all of them lie in the tangent plane of the ball.

A spherical segment is the part of a ball cut off from it by a plane. Circle ABC is the base of the spherical segment. The perpendicular segment MN drawn from the center N of circle ABC to the intersection with the spherical surface is the height of the spherical segment. Point M is the vertex of the spherical segment.

The surface area of ​​a spherical segment can be calculated using the formula:

The volume of a spherical segment can be found using the formula:

V = πh 2 (R – 1/3h),

where R is the radius of the great circle, h is the height of the spherical segment.

A spherical sector is obtained from a spherical segment and a cone as follows. If a spherical segment is smaller than a hemisphere, then the spherical segment is complemented by a cone, the vertex of which is in the center of the ball, and the base is the base of the segment. If the segment is larger than a hemisphere, then the specified cone is removed from it.

A spherical sector is a part of a ball bounded by a curved surface of a spherical segment (in our figure, this is AMCB) and a conical surface (in our figure, this is OABC), the base of which is the base of the segment (ABC), and the vertex is the center of the ball O.

The volume of the spherical sector is found by the formula:

V = 2/3 πR 2 H.

A spherical layer is a part of a ball enclosed between two parallel planes (planes ABC and DEF in the figure) intersecting the spherical surface. The curved surface of the spherical layer is called a spherical belt (zone). Circles ABC and DEF are the bases of the spherical belt. The distance NK between the bases of the spherical belt is its height.

website, when copying material in full or in part, a link to the original source is required.

A ball and a sphere are, first of all, geometric figures, and if a ball is a geometric body, then a sphere is the surface of a ball. These figures were of interest many thousands of years ago BC.

Subsequently, when it was discovered that the Earth is a ball and the sky is a celestial sphere, a new fascinating direction in geometry was developed - geometry on a sphere or spherical geometry. In order to talk about the size and volume of a ball, you must first define it.

Ball

A ball of radius R with a center at point O in geometry is a body that is created by all points in space that have a common property. These points are located at a distance not exceeding the radius of the ball, that is, they fill the entire space less than the radius of the ball in all directions from its center. If we consider only those points that are equidistant from the center of the ball, we will consider its surface or the shell of the ball.

How can I get the ball? We can cut a circle out of paper and start rotating it around its own diameter. That is, the diameter of the circle will be the axis of rotation. The formed figure will be a ball. Therefore, the ball is also called a body of revolution. Because it can be formed by rotating a flat figure - a circle.

Let's take some plane and cut our ball with it. Just like we cut an orange with a knife. The piece that we cut off from the ball is called a spherical segment.

In Ancient Greece, they knew how to not only work with a ball and sphere as geometric figures, for example, use them in construction, but also knew how to calculate the surface area of ​​a ball and the volume of a ball.

A sphere is another name for the surface of a ball. A sphere is not a body - it is the surface of a body of revolution. However, since both the Earth and many bodies have a spherical shape, for example a drop of water, the study of geometric relationships inside the sphere has become widespread.

For example, if we connect two points of a sphere with each other by a straight line, then this straight line is called a chord, and if this chord passes through the center of the sphere, which coincides with the center of the ball, then the chord is called the diameter of the sphere.

If we draw a straight line that touches the sphere at just one point, then this line will be called a tangent. In addition, this tangent to the sphere at this point will be perpendicular to the radius of the sphere drawn to the point of contact.

If we extend the chord to a straight line in one direction or the other from the sphere, then this chord will be called a secant. Or we can say it differently - the secant to the sphere contains its chord.

Ball volume

The formula for calculating the volume of a ball is:

where R is the radius of the ball.

If you need to find the volume of a spherical segment, use the formula:

V seg =πh 2 (R-h/3), h is the height of the spherical segment.

Surface area of ​​a ball or sphere

To calculate the area of ​​a sphere or the surface area of ​​a ball (they're the same thing):

where R is the radius of the sphere.

Archimedes was very fond of the ball and sphere, he even asked to leave a drawing on his tomb in which a ball was inscribed in a cylinder. Archimedes believed that the volume of a ball and its surface are equal to two-thirds of the volume and surface of the cylinder in which the ball is inscribed.”

Ball (sphere)

Spherical surface. Ball (sphere). Ball sections: circles.

Archimedes' theorem. Parts of the ball: spherical segment,

spherical layer, spherical belt, spherical sector.

Spherical surface - This locus of points(those. manynumber of all points)in space, equidistant from one point O , which is called the center of the spherical surface (Fig.90). Radius AOi diameter AB are defined in the same way as in a circle.

Ball (sphere) - This a body bounded by a spherical surface. Can get the ball by rotating the semicircle ( or circle ) around the diameter. All plane sections of the ball are circles ( Fig.90 ). The largest circle lies in a section passing through the center of the ball and is called big circle. Its radius is equal to the radius of the ball. Any two large circles intersect along the diameter of the ball ( AB, fig.91 ).This diameter is also the diameter of intersecting great circles. Through two points of a spherical surface located at the ends of the same diameter(A and B, Fig.91 ), you can draw countless large circles. For example, an infinite number of meridians can be drawn through the Earth's poles.

The volume of the sphere is one and a half times less than the volume of the cylinder circumscribed around it. (Fig.92 ), A the surface of the ball is one and a half times less than the total surface of the same cylinder ( Archimedes' theorem):

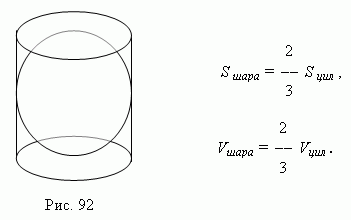
Here S ball And V ball - the surface and volume of the ball, respectively;

S cyl And V cyl - the total surface and volume of the circumscribed cylinder.

Parts of the ball. Part of a ball (sphere) ), cut off from it by some plane ( ABC, Fig.93), called ball(spherical ) segment. Circle ABC called basis ball segment. Line segment MN perpendicular drawn from the center N circle ABC until it intersects with a spherical surface, is called height ball segment. Dot M called top ball segment.

Part of a sphere enclosed between two parallel planes ABC and DEF intersecting a spherical surface (Fig. 93), called spherical layer; the curved surface of a spherical layer is called ball belt(zone). Circles ABC and DEF – grounds ball belt. Distance N.K. between the bases of the spherical belt - its height. The part of the ball bounded by the curved surface of a spherical segment ( AMCB, Fig.93) and conical surface OABC , the base of which is the base of the segment ( ABC ), and the vertex is the center of the ball O , called spherical sector.

When people are asked the difference between a sphere and a ball, many simply shrug their shoulders, thinking that in fact they are the same thing (the analogy with a circle and a circle). Indeed, do all of us know geometry well from the school curriculum and can immediately answer this question? A sphere has some differences from a ball, which not only schoolchildren need to know in order to get a good grade for their demonstrated knowledge, but also many other people, for example, whose work is directly related to drawings.

Definition

Ball– the set of all points in space. All these points are located from the center of the geometric body at a distance that is no more than a given one. This distance itself is called the radius. A ball, as a geometric body, is formed as follows: a semicircle rotates near its diameter. As for the sphere, this is the surface of the ball (for example, a closed ball includes it, an open one does not). Calculating the area or volume of a ball involves entire geometric formulas that are very complex, despite the apparent simplicity of the geometric figure itself.

Sphere, as noted above, is the surface of the ball, its shell. All points in space are equidistant from the center of the sphere. As for the radius of a geometric body, it is called any segment, one point of which is directly the center of the sphere, and the other can be located at any point on the surface. We can say that a sphere is the shell of a ball without any content (more specific examples will be given below). Just like a ball, a sphere is a body of revolution. By the way, many also wonder what is the difference between a circle and a circle from a sphere and a ball. Everything is simple here: in the first case these are figures on a plane, in the second - in space.

Comparison

It has already been said that a sphere is the surface of a ball, which already makes it possible to talk about one significant sign of difference. The difference between the two geometric bodies is observed in some other aspects:

• All points of the ball are at the same distance from the center, while the body is limited by the surface (a sphere that is empty inside). In other words, the sphere is hollow. Usually, for ease of understanding, a simple example is given with a balloon and a billiard ball. Both of these objects are called balls, but in the first case we are dealing with a sphere, and in the second with a full-fledged ball with its own contents inside.
• A sphere has its own area, but it has no volume. A sphere is the opposite: its volume can be calculated, while it has no area. Some may say that this is the main sign of difference, but it only appears if it is necessary to make some calculations (complex geometric formulas). Therefore, the main difference is that the sphere is hollow, and the ball is a body with contents inside.
• Another difference lies in the radius. For example, the radius of a sphere is not only the distance of points to the center. A radius can be any segment connecting a point on a sphere to its center. All these segments are equal to each other. As for the ball, the points lying inside it are less than a radius away from the center (precisely because of the sphere bounding it).

Conclusions website

1. A sphere is hollow, while a ball is a body filled inside. For example, a hot air balloon is a sphere, a billiard ball is a full-fledged ball.
2. A sphere has area and no volume, but a sphere does the opposite.
3. The third difference is the measurement of the radius of two geometric bodies.

Definition.

A sphere can be described as a three-dimensional figure that is formed by rotating a circle around its diameter by 180° or a semicircle around its diameter by 360°.

Definition.

A ball can be described as a three-dimensional figure that is formed by rotating a circle around its diameter by 180° or a semicircle around its diameter by 360°.

Definition. Radius of the sphere (ball)(R) is the distance from the center of the sphere (ball) O to any point on the sphere (surface of the ball).

Definition. Sphere (ball) diameter(D) is a segment connecting two points of a sphere (the surface of a ball) and passing through its center.

Formula. Sphere volume:

Formula. Surface area of ​​a sphere through radius or diameter:

S = 4π R 2 = π D 2

Sphere equation

1. Equation of a sphere with radius R and center at the origin of the Cartesian coordinate system:

x 2 + y 2 + z 2 = R 2

2. Equation of a sphere with radius R and center at a point with coordinates (x 0, y 0, z 0) in the Cartesian coordinate system:

(x - x 0) 2 + (y - y 0) 2 + (z - z 0) 2 = R 2

Definition. Diametrically opposite points are any two points on the surface of a ball (sphere) that are connected by a diameter.

Basic properties of a sphere and a ball

1. All points of the sphere are equally distant from the center.

2. Any section of a sphere by a plane is a circle.

3. Any section of a ball by a plane is a circle.

4. The sphere has the largest volume among all spatial figures with the same surface area.

5. Through any two diametrically opposite points you can draw many great circles for a sphere or circles for a ball.

6. Through any two points, except diametrically opposite points, you can draw only one large circle for a sphere or a large circle for a ball.

7. Any two great circles of one ball intersect along a straight line passing through the center of the ball, and the circles intersect at two diametrically opposite points.

8. If the distance between the centers of any two balls is less than the sum of their radii and greater than the modulus of the difference of their radii, then such balls intersect, and a circle is formed in the intersection plane.

Secant, chord, secant plane of a sphere and their properties

Definition. Sphere secant is a straight line that intersects the sphere at two points. The intersection points are called piercing points surfaces or entry and exit points on the surface.

Definition. Chord of a sphere (ball)- this is a segment connecting two points on a sphere (the surface of a ball).

Definition. Cutting plane is the plane that intersects the sphere.

Definition. Diametral plane- this is a secant plane passing through the center of a sphere or ball, the section forms accordingly large circle And big circle. The great circle and great circle have a center that coincides with the center of the sphere (ball).

Any chord passing through the center of a sphere (ball) is a diameter.

A chord is a segment of a secant line.

The distance d from the center of the sphere to the secant is always less than the radius of the sphere:

d< R

The distance m between the cutting plane and the center of the sphere is always less than the radius R:

m< R

The location of the section of the cutting plane on the sphere will always be small circle, and on the ball the section will be small circle. The small circle and small circle have their own centers that do not coincide with the center of the sphere (ball). The radius r of such a circle can be found using the formula:

r = √R 2 - m 2,

Where R is the radius of the sphere (ball), m is the distance from the center of the ball to the cutting plane.

Definition. Hemisphere (hemisphere)- this is half of a sphere (ball), which is formed when it is cut by a diametrical plane.

Tangent, tangent plane to a sphere and their properties

Definition. Tangent to a sphere- This is a straight line that touches the sphere at only one point.

Definition. Tangent plane to a sphere is a plane that touches the sphere at only one point.

The tangent line (plane) is always perpendicular to the radius of the sphere drawn to the point of contact

The distance from the center of the sphere to the tangent line (plane) is equal to the radius of the sphere.

Definition. Ball segment- this is the part of the ball that is cut off from the ball by a cutting plane. Basis of the segment called the circle that formed at the site of the section. Segment height h is the length of the perpendicular drawn from the middle of the base of the segment to the surface of the segment.

Formula. Outer surface area of ​​a sphere segment with height h through the radius of the sphere R:

S = 2πRh