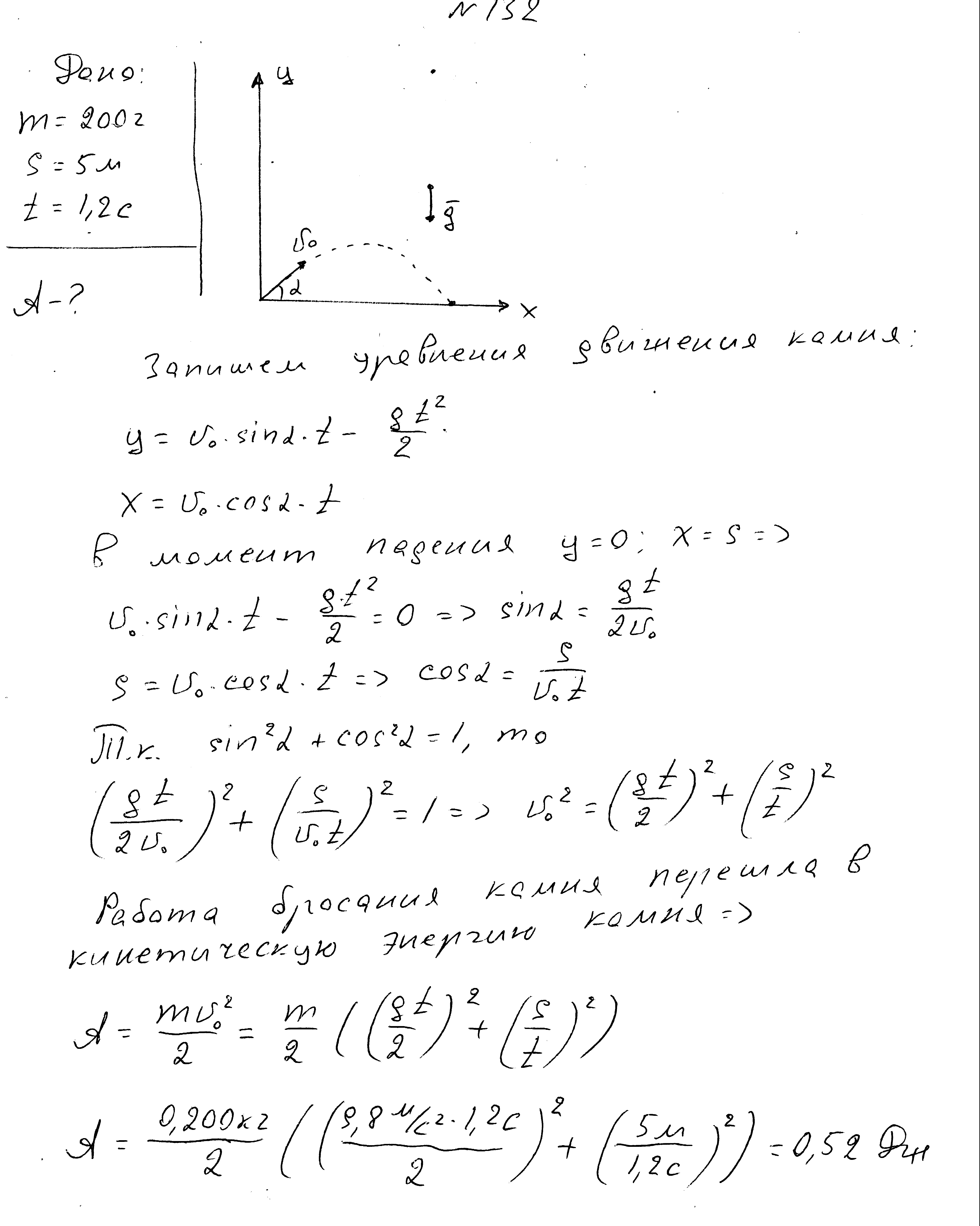Study of the motion of a body thrown at an angle to the horizontal. The movement of a body thrown at an angle to the horizon! Physics: motion of a body thrown at an angle to the horizontal

If a body is thrown at an angle to the horizon, then in flight it is acted upon by the force of gravity and the force of air resistance. If the resistance force is neglected, then the only force left is gravity. Therefore, due to Newton’s 2nd law, the body moves with acceleration equal to the acceleration of gravity; projections of acceleration onto the coordinate axes ax = 0, ay = - g.

Figure 1. Kinematic characteristics of a body thrown at an angle to the horizontal

Any complex movement of a material point can be represented as a superposition of independent movements along the coordinate axes, and in the direction of different axes the type of movement may differ. In our case, the motion of a flying body can be represented as the superposition of two independent motions: uniform motion along the horizontal axis (X-axis) and uniformly accelerated motion along the vertical axis (Y-axis) (Fig. 1).

The body's velocity projections therefore change with time as follows:

where $v_0$ is the initial speed, $(\mathbf \alpha )$ is the throwing angle.

With our choice of origin, the initial coordinates (Fig. 1) are $x_0=y_0=0$. Then we get:

(1)

Let's analyze formulas (1). Let us determine the time of motion of the thrown body. To do this, let's set the y coordinate equal to zero, because at the moment of landing the height of the body is zero. From here we get for the flight time:

The second time value at which the height is zero is zero, which corresponds to the moment of throwing, i.e. this value also has a physical meaning.

We obtain the flight range from the first formula (1). The flight range is the value of the x coordinate at the end of the flight, i.e. at time equal to $t_0$. Substituting value (2) into the first formula (1), we get:

From this formula it can be seen that the greatest flight range is achieved at a throwing angle of 45 degrees.

The maximum lifting height of the thrown body can be obtained from the second formula (1). To do this, you need to substitute a time value equal to half the flight time (2) into this formula, because It is at the midpoint of the trajectory that the flight altitude is maximum. Carrying out calculations, we get

From equations (1) one can obtain the equation of the body’s trajectory, i.e. an equation relating the x and y coordinates of a body during motion. To do this, you need to express time from the first equation (1):

and substitute it into the second equation. Then we get:

This equation is the motion trajectory equation. It can be seen that this is the equation of a parabola with its branches down, as indicated by the “-” sign in front of the quadratic term. It should be borne in mind that the throwing angle $\alpha $ and its functions are simply constants here, i.e. constant numbers.

A body is thrown with speed v0 at an angle $(\mathbf \alpha )$ to the horizontal. Flight time $t = 2 s$. To what height Hmax will the body rise?

$$t_B = 2 s$$ $$H_max - ?$$

The law of body motion has the form:

$$\left\( \begin(array)(c) x=v_(0x)t \\ y=v_(0y)t-\frac(gt^2)(2) \end(array) \right.$ $

The initial velocity vector forms an angle $(\mathbf \alpha )$ with the OX axis. Hence,

\ \ \

A stone is thrown from the top of a mountain at an angle = 30$()^\circ$ to the horizon with an initial speed of $v_0 = 6 m/s$. Inclined plane angle = 30$()^\circ$. How far from the throwing point will the stone land?

$$ \alpha =30()^\circ$$ $$v_0=6\ m/s$$ $$S - ?$$

Let's place the origin of coordinates at the throwing point, OX - along the inclined plane downwards, OY - perpendicular to the inclined plane upwards. Kinematic characteristics of movement:

Law of motion:

$$\left\( \begin(array)(c) x=v_0t(cos 2\alpha +g\frac(t^2)(2)(sin \alpha \ )\ ) \\ y=v_0t(sin 2 \alpha \ )-\frac(gt^2)(2)(cos \alpha \ ) \end(array) \right.$$ \

Substituting the resulting value $t_В$, we find $S$:

There were 3 seconds left before the end of the final match of the basketball tournament of the 1972 Munich Olympics. The Americans - the US team - were already celebrating their victory! Our team - the USSR national team - won by about 10 points against the great dream Team...

A few minutes before the end of the match. But, having lost all the advantage in the end, she was already losing one point 49:50. Then the incredible happened! Ivan Edeshko throws the ball from behind the end line across the entire court under the American ring, where our center Alexander Belov receives the ball, surrounded by two opponents, and puts it into the basket. 51:50 – we are Olympic champions!!!

As a child then, I experienced the strongest emotions - first disappointment and resentment, then crazy delight! The emotional memory of this episode is etched into my consciousness for the rest of my life! Watch the video on the Internet at the request of “Alexander Belov’s golden throw”, you won’t regret it.

The Americans then did not admit defeat and refused to receive silver medals. Is it possible to do in three seconds what our players did? Let's remember physics!

In this article, we will look at the movement of a body thrown at an angle to the horizon, create a program in Excel for solving this problem with various combinations of input data, and try to answer the question posed above.

This is a fairly well-known problem in physics. In our case, the body thrown at an angle to the horizontal is a basketball. We will calculate the initial speed, time and trajectory of a ball thrown across the entire court by Ivan Edeshko and falling into the hands of Alexander Belov.

Mathematics and physics of basketball flight.

The formulas and calculations presented below areexcel are universal for a wide range of problems about bodies thrown at an angle to the horizon and flying along a parabolic trajectory without taking into account the influence of air friction.

The calculation diagram is presented in the figure below. Launch MS Excel or OOo Calc.

Initial data:

1. Since we are on planet Earth and are considering a ballistic problem - the movement of bodies in the Earth’s gravitational field, the first thing we will do is write down the main characteristic of the gravitational field - the acceleration of free fall g in m/s 2

to cell D3: 9,81

2. The dimensions of the basketball court are 28 meters long and 15 meters wide. The horizontal distance of the ball from almost the entire court to the ring from the opposite baseline x write in meters

to cell D4: 27,000

3. If we assume that Edeshko made the throw from a height of about two meters, and Belov caught the ball just somewhere at the level of the hoop, then with a basketball hoop height of 3.05 meters, the vertical distance between the points of departure and arrival of the ball will be 1 meter. Let's write down the vertical displacement y in meters

to cell D5: 1,000

4. According to my measurements on the video recording, the ball launch angle α 0 from Edeshko’s hands did not exceed 20°. Let's enter this value

to cell D6: 20,000

Calculation results:

Basic equations describing the motion of a body thrown at an angle to the horizon without taking into account air resistance:

x =v 0*cos α 0 *t

y =v 0*sin α 0 *t -g *t 2 /2

5. Let's express time t from the first equation, substitute it into the second and calculate the initial speed of the ball v 0 in m/s

in cell D8: =(D3*D4^2/2/COS (RADIANS(D6))^2/(D4*TAN (RADIANS(D6)) -D5))^0.5 =21,418

v 0 =(g *x 2 /(2*(cosα 0 ) 2 *(x *tgα 0 -y )) 0.5

6. Ball flight time from Edeshko's hands to Belov's hands t Let's calculate in seconds, knowing now v 0 , from the first equation

in cell D9: =D4/D8/COS (RADIANS(D6)) =1,342

t = x /(v 0 * cosα 0 )

7. Let's find the direction angle of the ball's flight speed α i at the trajectory point of interest to us. To do this, we write the initial pair of equations in the following form:

y =x *tgα 0 -g *x 2 /(2*v 0 2*(cosα 0 ) 2)

This is the equation of a parabola - a flight path.

We need to find the angle of inclination of the tangent to the parabola at the point of interest to us - this will be the angle α i. To do this, take the derivative, which is the tangent of the tangent angle:

y' =tgα 0 -g *x /(v 0 2*(cosα 0 ) 2)

Let's calculate the angle of arrival of the ball into Belov's hands α i in degrees

in cell D10: =ATAN (TAN (RADIANS(D6)) -D3*D4/D8^2/COS (RADIANS(D6))^2)/PI()*180 =-16,167

α i = arctgy ’ = arctg(tgα 0 — g * x /(v 0 2 *(cosα 0 ) 2))

The calculation in Excel is basically complete.

Other payment options:

Using the written program, you can quickly and easily perform calculations with other combinations of initial data.

Let given horizontal x = 27 meters , vertical y = 1 meter flight range and initial speed v 0 = 25 m/s.

We need to find the flight time t and departure angles α 0 and arrival α i

Let's use the MS Excel service “Parameter Selection”. I have repeatedly explained in detail how to use it in several blog articles. You can read more about using this service.

We set the value in cell D8 to 25,000 by changing the value in cell D6 by selecting it. The result is in the picture below.

The source data in this version of the calculation in Excel (as well as in the previous one) are highlighted in blue frames, and the results are outlined in red rectangular frames!

Setting in tableExcel some value of interest in one of the cells with a light yellow fill by selecting a changed value in one of the cells with a light turquoise fill, you can generally get ten different options for solving the problem of the motion of a body thrown at an angle to the horizon for ten different sets original data!!!

Answer to the question:

Let's answer the question posed at the beginning of the article. The ball sent by Ivan Edeshko flew to Belov in 1.342 seconds, according to our calculations. Alexander Belov caught the ball, landed, jumped and threw. He had a lot of time for all this - 1.658 seconds! This is really a sufficient amount of time to spare! A detailed review of the video footage confirms the above. Our players had three seconds to deliver the ball from their end line to the opponents' backboard and throw it into the hoop, writing their names in gold in the history of basketball!

I beg respectful author's work download file after subscription for article announcements!

Free fall represents a special case of uniformly accelerated motion without initial speed. The acceleration of this movement is equal to the acceleration of gravity, also called the acceleration of gravity. For this movement the formulas are valid:

u t
g
h- the height from which the body falls
t- time during which the fall continued

Note:

• Air resistance is not taken into account in these formulas.
• The acceleration of gravity has the given value (9.81 (m/s?)) near the earth's surface. The value of g changes at other distances from the Earth's surface!

Movement of a body thrown vertically upward

A body thrown vertically upwards moves uniformly slowly with an initial speed u0 and acceleration a = -g. Movement of a body over time t represents the lift height h.For this movement the following formulas are valid:

U0- initial speed of body movement
U- the speed at which a body falls after time t
g- free fall acceleration, 9.81 (m/s?)
h- the height to which the body will rise in time t
t- time

Body speed at a certain height:

Maximum lifting height:

Time to rise to maximum height:

Addition of movements directed at an angle to each other.

The body can simultaneously participate in several translational movements. Since acceleration, speed and displacement are vector quantities, they can be added according to the laws of vector (geometric) addition. Those. according to the parallelogram rule.

The resulting value of any movement characteristic can be calculated.

If:
Up- the resulting instantaneous speed,
U1- instantaneous speed of the first movement,
U2- instantaneous speed of the second movement,
? - the angle formed by the velocity vectors u1 And u2,
Then, using the cosine theorem, we get:

If movements 1 and 2 occur at right angles to each other, then the formula simplifies because

The movement of a body thrown horizontally.

The motion of a body thrown horizontally is a combination of two motions mutually perpendicular to each other:
- horizontal (uniform) movement,
- vertical (free fall)

Equation of the trajectory of a body thrown horizontally

If we construct the trajectory of a body thrown horizontally in the coordinate system xy, taking the throwing point as the origin of the coordinates, and the direction of the ordinate axis coinciding with the direction of the free fall acceleration vector, then the coordinates of each point of the trajectory represent the movement of the body in the horizontal direction (movement at a constant speed U0) and in the vertical direction (uniformly accelerated movement with acceleration g)

x, y- body coordinates,
u0
g
t- travel time (s)

Equation of the trajectory of a body thrown horizontally as follows:

g and initial speed of the body u0 are constant quantities, then the coordinate y proportional to the square x, i.e. the trajectory of movement is a parabola, the vertex of which is at the starting point of movement.

Vector position of a body thrown horizontally, formula

The position of each point of the trajectory of a body thrown horizontally can be specified by the position vector r, which represents the resulting displacement:

or Position vector:

x-coordinate:

Y-coordinate:

Note: Air resistance is not taken into account in the formulas.

Equation of motion of a body thrown at an angle to the horizontal.

The coordinates of the trajectory point are described by the equations:

x, y- body coordinates
U0- initial body speed (m/s)
? - the angle at which the body is thrown to the horizon (°)
g- free fall acceleration 9.81 (m/s2)
t- travel time (s)

From the formulas through the parameter t we derive the general equation of motion of a body thrown at an angle to the horizontal

Since the acceleration of gravity g, ? - the angle at which the body is thrown to the horizon and the initial speed of the body u0 are constant quantities, then the coordinate y proportional to the square x, i.e. the trajectory of movement is a parabola, the starting point is on one of its branches, and the top of the parabola is the point of maximum elevation of the body.

Time of rise to maximum height of a body thrown at an angle to the horizon.

The time to rise to the maximum height is determined from the condition that the vertical component of the instantaneous speed is zero

from this equation we get:

U0- initial speed of the body (m/s),
?
g- free fall acceleration 9.81 (m/s2),
thmax- time to rise to maximum height (s)

The throw distance of a body thrown at an angle to the horizontal.

Throw range or damage radius determined by the formulas for the total time of movement and the formula for body coordinates

substituting tsmax into the expression and simplifying we get:

U0- initial speed of the body (m/s),
? - the angle at which the body is thrown to the horizon (°),
g- free fall acceleration 9.81 (m/s2),
tsmax- total travel time (s)

Movement of a body thrown at an angle to the horizontal

Let us consider the movement of a body thrown with a speed V 0, the vector of which is directed at an angle α to the horizon, in the XOY plane, placing the body at the moment of throwing at the origin of coordinates, as shown in Figure 1.

In the absence of resistance forces, the motion of a body thrown at an angle to the horizon can be considered as a special case of curvilinear motion under the influence of gravity. Applying Newton's 2nd law

Figure 1 is directed upwards, in the case when the OY axis is directed downward, then the projection of the vector

2 a on the op-amp axis will be positive(reading the conditions of the problems, choose the direction of the axes yourself, if this is not stated in the conditions).

The values ​​of the projections of the acceleration vector a on the OX and OU axes give reason to make

the following output:

∙ a body thrown at an angle to the horizontal simultaneously participates in two movements - uniform horizontally and uniformly variable along

For uniformly variable motion, the dependences of speed and displacement on time are given by the equations:

coordinates of the body at time t.

During its movement t (from the moment of throwing to the moment of falling on the same

level) the body rises to a maximum height hmax, descends from it and flies away from the throwing point at a distance L (flight range) - see Figure 1.

1) Body movement time t can be found taking into account the values ​​of body coordinates Sy in

Substituting the values ​​of Voy and (14) into the second equation of system (13), we obtain

2) Flight range L can be found, taking into account the values ​​of the body coordinates Sх in

initial moment of time and at time t (see Fig. 1)

Substituting the values ​​of Vox and (17) into the first equation of system (13), we obtain

3) Maximum lifting height h max can be found given the value

body velocity V at the point of maximum lift of the body

Comparison of values ​​(16) and (22) gives grounds to conclude

· time of movement to the height of maximum body lift (t under ) is equal to the time of descent of the body (tп) from this height and is equal to half the time of the entire movement of the body from the moment of throwing to the moment of falling to the same level

Studying the motion of a body thrown with a speed V 0, the vector of which is directed at an angle α to the horizontal, in the XOY plane, is very clear on a computer model

"Free fall of bodies" in the collection of computer models "Open Physics"

PHYSICON company. In this model, you can set different initial conditions.

For example, the case we considered must be specified (the “Clear” command) with the initial condition h = 0 and selected V0 and α. The "Start" command will demonstrate the movement of the body and give a picture of the trajectory of movement and the direction of the body's velocity vectors at fixed moments in time.

Fig.2. Dialog window of the computer model "Free fall of bodies" in the section

"Mechanics"; a body moves from the origin and falls at the same level.

If the condition of the problem differs from the case we considered, then it is necessary

to solve the problem, choosing the direction of the axes, place the body at the initial moment

time, depict the trajectory of the body to the point of fall, thus

by determining the coordinates of the body at the initial and final moments of time. Then

use equations (3), (5), (8) and (9) as a basis for the solution and discussed above

algorithm for solving the problem.

Let's consider special cases.

6 1. The body was thrown at speed V 0 , whose vector is directed at an angleα to

horizon, from a height h and it fell at a distance L from the point of throwing. y to initial

and the values ​​of the remaining coordinates will be selected in the same way as we selected.

Fig.3. Dialog window of the computer model "Free fall of bodies" in the section

"Mechanics"; the body moves from point h = 50m and falls to zero level.

2. A body was thrown horizontally with a speed V 0 from a height h and it fell at a distance L from the point of throwing. The difference from the case we considered is that the values ​​of the body coordinates S y at the initial moment will also be determined by equation (25),

and the values ​​of the remaining coordinates will be selected in the same way as we selected. But in this case, the initial velocity of the body in projection onto the OU axis is equal to zero (since α = 0), i.e.

the projections of the initial velocity vector on the OX and OU axes are equal

Fig.4. Dialog window of the computer model "Free fall of bodies" in the section

"Mechanics"; a body thrown horizontally moves from point h = 50m and falls to zero level.

Below are the conditions of the problems and scanned solutions. If you need to solve a problem on this topic, you can find a similar condition here and solve yours by analogy. The page may take some time to load due to the large number of images. If you need problem solving or online help in physics, please contact us, we will be happy to help.

The principle of solving these problems is to decompose the speed of a freely falling body into two components - horizontal and vertical. The horizontal component of the velocity is constant, the vertical movement occurs with the acceleration of free fall g=9.8 m/s 2 . The law of conservation of mechanical energy can also be applied, according to which the sum of the potential and kinetic energy of the body in this case is constant.

A material point is thrown at an angle to the horizon with an initial speed of 15 m/s. The initial kinetic energy is 3 times greater than the kinetic energy of the point at the top point of the trajectory. How high did the point rise?

A body is thrown at an angle of 40 degrees to the horizontal with an initial speed of 10 m/s. Find the distance that the body will fly before falling, the height of rise at the top point of the trajectory and the time in flight.

A body is thrown down from a tower of height H, at an angle α to the horizontal, with an initial speed v. Find the distance from the tower to the place where the body fell.

A body with a mass of 0.5 kg is thrown from the surface of the Earth at an angle of 30 degrees to the horizontal, with an initial speed of 10 m/s. Find the potential and kinetic energies of the body after 0.4 s.

A material point is thrown upward from the Earth's surface at an angle to the horizon with an initial speed of 10 m/s. Determine the speed of a point at a height of 3 m.

A body is thrown upward from the Earth's surface at an angle of 60 degrees with an initial speed of 10 m/s. Find the distance to the point of impact, the speed of the body at the point of impact and the time in flight.

A body is thrown upward at an angle to the horizontal with an initial speed of 20 m/s. The distance to the fall point is 4 times the maximum lift height. Find the angle at which the body is thrown.

A body is thrown from a height of 5 m at an angle of 30 degrees to the horizontal with an initial speed of 22 m/s. Find the flight range of the body and the time of flight of the body.

A body is thrown from the Earth's surface at an angle to the horizon with an initial speed of 30 m/s. Find the tangential and normal accelerations of the body 1s after the throw.

A body is thrown from the surface of Zesli at an angle of 30 degrees to the horizontal with an initial speed of 14.7 m/s. Find the tangential and normal accelerations of the body 1.25 s after the throw.

A body is thrown at an angle of 60 degrees to the horizontal with an initial speed of 20 m/s. After what time will the angle between the speed and the horizon become 45 degrees?

Ball thrown in the gym at an angle to the horizon,with an initial speed of 20 m/s, at the top point of the trajectory it touched the ceiling at a height of 8 m and fell at some distance from the place of the throw. Find this distance and the angle at which the body is thrown.

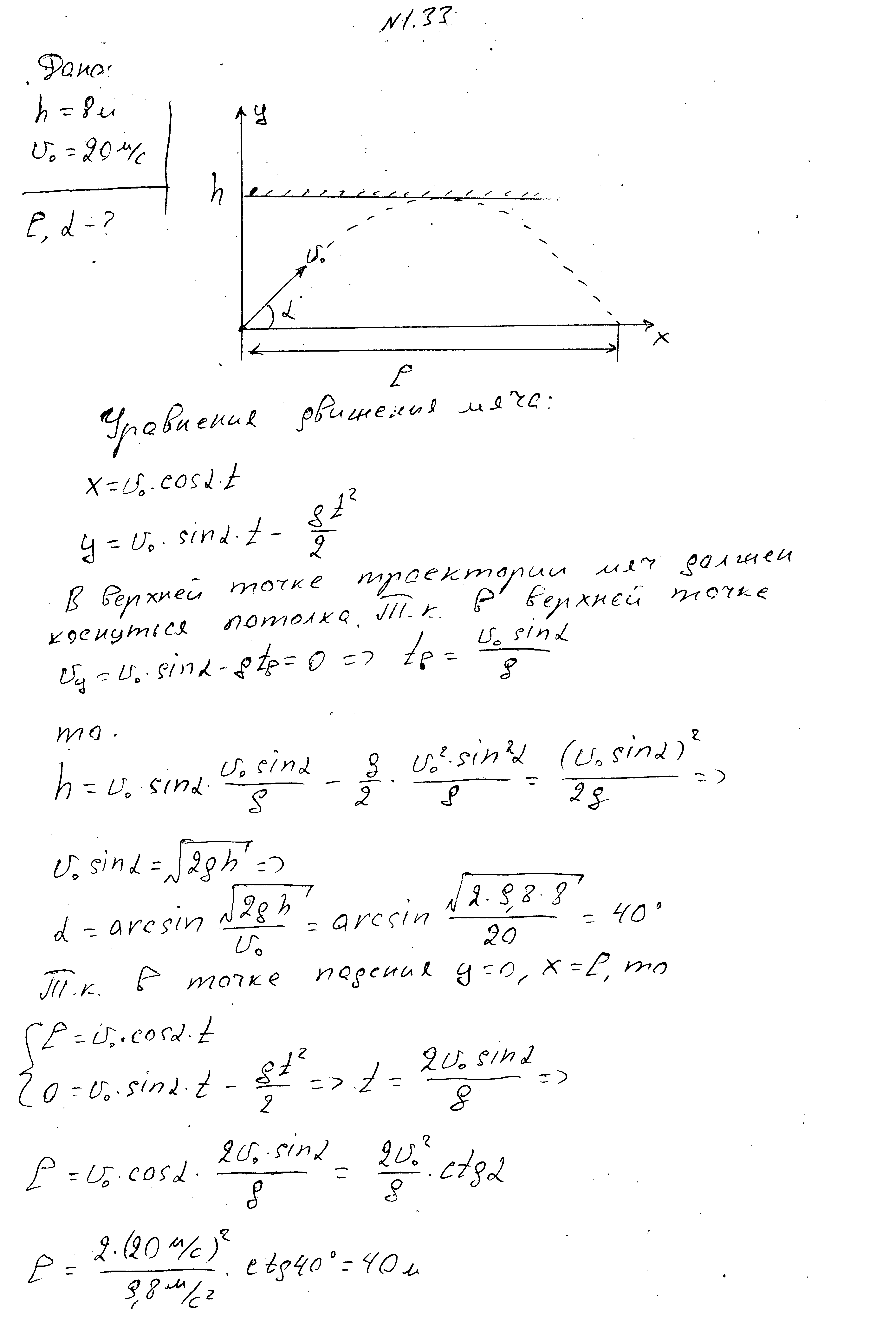
A body thrown from the surface of the Earth at an angle to the horizon fell after 2.2 s. Find the maximum lifting height of the body.

A stone is thrown at an angle of 30 degrees to the horizontal. The stone reached a certain height twice - 1 s and 3 s after being thrown. Find this height and the initial speed of the stone.

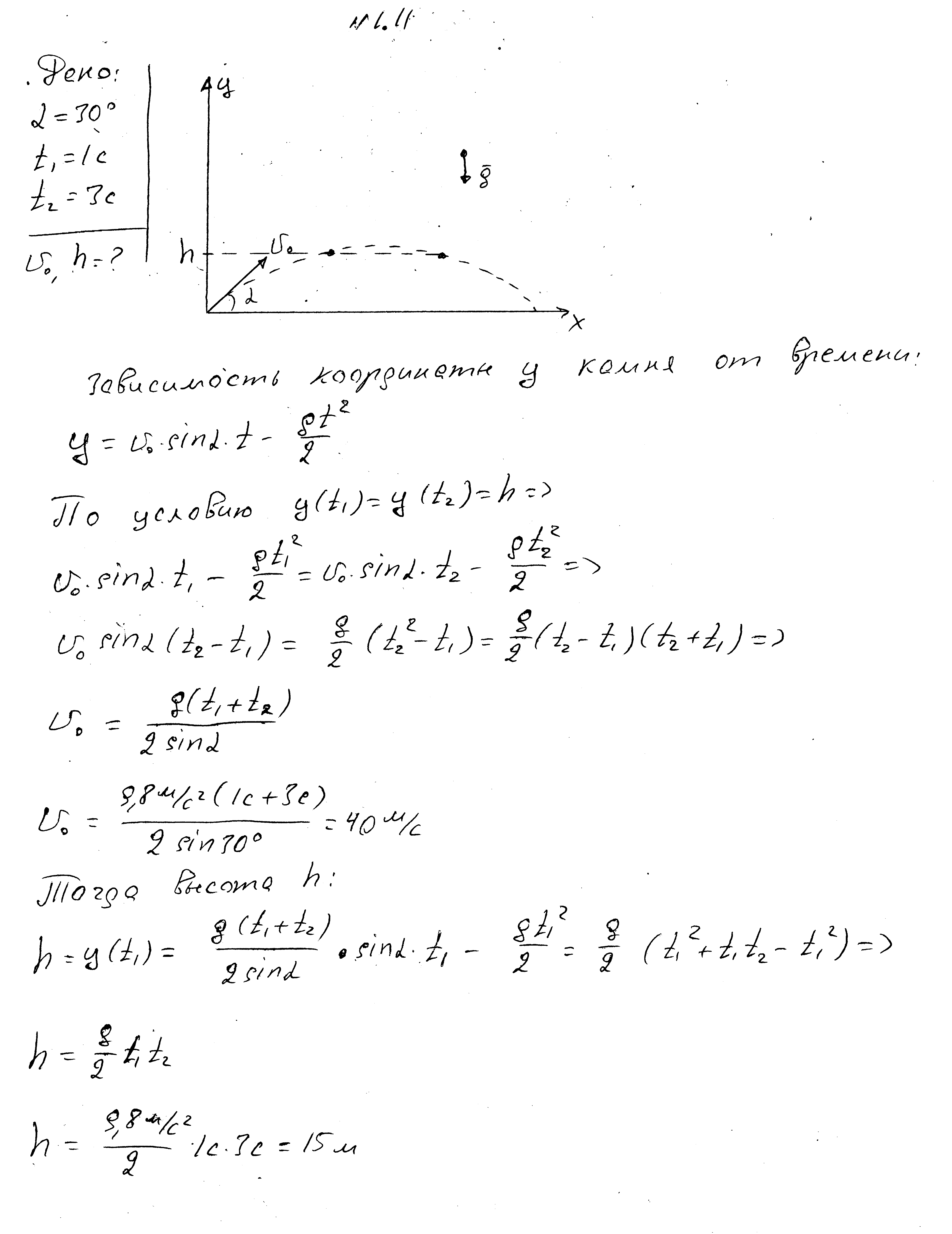
A stone is thrown at an angle of 30 degrees to the horizontal with an initial speed of 10 m/s. Find the distance from the throwing point to the stone after 4 s.

The projectile is fired at the moment when the plane flies over the gun, at an angle to the horizon with an initial speed of 500 m/s. The shell hit the plane at an altitude of 3.5 km 10 seconds after being fired. What is the speed of the plane?

A cannonball with a mass of 5 kg is thrown from the surface of the Earth at an angle of 60 degrees to the horizontal. The energy spent to accelerate the weight is 500 J. Determine the flight range and flight time.

A body is thrown down from a height of 100 m at an angle of 30 degrees to the horizontal with an initial speed of 5 m/s. Find the flight range of the body.

A body with a mass of 200 g, thrown from the surface of the Earth at an angle to the horizon, fell at a distance of 5 m after a time of 1.2 s. Find a body throwing job.