Simplificação de equações trigonométricas. Transformações de identidade de expressões trigonométricas
A videoaula "Simplificação de expressões trigonométricas" foi projetada para desenvolver as habilidades dos alunos na resolução de problemas trigonométricos usando identidades trigonométricas básicas. Durante a videoaula, são considerados tipos de identidades trigonométricas, exemplos de resolução de problemas usando-as. Usando recursos visuais, é mais fácil para o professor atingir os objetivos da aula. Uma apresentação vívida do material contribui para a memorização de pontos importantes. O uso de efeitos de animação e dublagem permitem substituir completamente o professor na fase de explicação do material. Assim, usando esse auxílio visual nas aulas de matemática, o professor pode aumentar a eficácia do ensino.
No início da videoaula, seu tema é anunciado. Em seguida, as identidades trigonométricas estudadas anteriormente são lembradas. A tela exibe as igualdades sen 2 t+cos 2 t=1, tg t=sen t/cos t, onde t≠π/2+πk para kϵZ, ctg t=cos t/sen t, verdadeiro para t≠πk, onde kϵZ, tan t · ctg t=1, em t≠πk/2, onde kϵZ, chamadas identidades trigonométricas básicas. Note-se que estas identidades são frequentemente utilizadas na resolução de problemas onde é necessário provar a igualdade ou simplificar a expressão.
Além disso, são considerados exemplos da aplicação dessas identidades na resolução de problemas. Em primeiro lugar, propõe-se considerar a resolução de problemas de simplificação de expressões. No exemplo 1, é necessário simplificar a expressão cos 2 t- cos 4 t+ sin 4 t. Para resolver o exemplo, o fator comum cos 2 t é colocado entre parênteses. Como resultado de tal transformação entre parênteses, é obtida a expressão 1-cos 2 t, cujo valor da identidade básica da trigonometria é igual a sen 2 t. Após a transformação da expressão, é óbvio que mais um fator comum sen 2 t pode ser retirado dos colchetes, após o que a expressão assume a forma sen 2 t (sen 2 t + cos 2 t). Da mesma identidade básica, deduzimos o valor da expressão entre parênteses igual a 1. Como resultado da simplificação, obtemos cos 2 t- cos 4 t+ sen 4 t= sen 2 t.
No exemplo 2, a expressão custo/(1- sint)+ custo/(1+ sint) também precisa ser simplificada. Como a expressão custo está nos numeradores de ambas as frações, pode ser destacada como um fator comum. Em seguida, as frações entre parênteses são reduzidas a um denominador comum multiplicando (1- sint)(1+ sint). Após a redução de termos semelhantes, 2 permanece no numerador e 1 - sen 2 t no denominador. No lado direito da tela, a identidade trigonométrica básica sen 2 t+cos 2 t=1 é recuperada. Usando-o, encontramos o denominador da fração cos 2 t. Depois de reduzir a fração, obtemos uma forma simplificada da expressão custo / (1- sint) + custo / (1 + sint) \u003d 2 / custo.
Em seguida, consideramos exemplos de prova de identidades em que o conhecimento adquirido sobre as identidades básicas da trigonometria é aplicado. No Exemplo 3, é necessário provar a identidade (tg 2 t-sen 2 t)·ctg 2 t=sen 2 t. O lado direito da tela exibe três identidades que serão necessárias para a prova - tg t ctg t=1, ctg t=cos t/sin te tg t=sin t/cos t com restrições. Para provar a identidade, os colchetes são abertos primeiro, após o que é formado um produto que reflete a expressão da identidade trigonométrica principal tg t·ctg t=1. Então, de acordo com a identidade da definição de cotangente, ctg 2 t é transformado. Como resultado das transformações, obtém-se a expressão 1-cos 2 t. Usando a identidade básica, encontramos o valor da expressão. Assim, prova-se que (tg 2 t-sen 2 t)·ctg 2 t=sen 2 t.

No exemplo 4, você precisa encontrar o valor da expressão tg 2 t+ctg 2 t se tg t+ctg t=6. Para avaliar a expressão, os lados direito e esquerdo da equação (tg t+ctg t) 2 =6 2 são primeiro ao quadrado. A fórmula de multiplicação abreviada é exibida no lado direito da tela. Após abrir os colchetes do lado esquerdo da expressão, forma-se a soma tg 2 t+2 tg t ctg t+ctg 2 t, para cuja transformação se pode aplicar uma das identidades trigonométricas tg t ctg t=1, cuja forma é recuperada no lado direito da tela. Após a transformação, obtém-se a igualdade tg 2 t+ctg 2 t=34. O lado esquerdo da igualdade coincide com a condição do problema, então a resposta é 34. O problema está resolvido.
A videoaula "Simplificando expressões trigonométricas" é recomendada para uso em uma aula tradicional de matemática escolar. Além disso, o material será útil para um professor que oferece ensino a distância. A fim de formar uma habilidade na resolução de problemas trigonométricos.
INTERPRETAÇÃO DO TEXTO:
"Simplificação de expressões trigonométricas".
Igualdade
1) sen 2 t + cos 2 t = 1 (seno ao quadrado te mais cosseno ao quadrado te é igual a um)
2) tgt =, em t ≠ + πk, kϵZ (a tangente de te é igual à razão entre o seno de te e o cosseno de te quando te não é igual a pi por dois mais pi ka, ka pertence a zet)
3) ctgt = , em t ≠ πk, kϵZ (a cotangente de te é igual à razão entre o cosseno de te e o seno de te quando te não é igual ao pico de ka, que pertence a z).
4)tgt ∙ ctgt = 1 para t ≠ , kϵZ
são chamadas de identidades trigonométricas básicas.
Muitas vezes eles são usados para simplificar e provar expressões trigonométricas.
Considere exemplos de uso dessas fórmulas ao simplificar expressões trigonométricas.
EXEMPLO 1. Simplifique a expressão: cos 2 t - cos 4 t + sin 4 t. (expressão um cosseno ao quadrado te menos cosseno do quarto grau de te mais seno do quarto grau de te).
Solução. cos 2 t - cos 4 t + sen 4 t = cos 2 t∙ (1 - cos 2 t) + sen 4 t = cos 2 t ∙ sen 2 t + sen 4 t = sen 2 t (cos 2 t + sen 2 t) = sen 2 t 1 = sen 2 t
(tiramos o fator comum cosseno quadrado te, entre parênteses obtemos a diferença entre a unidade e o quadrado do cosseno te, que é igual ao quadrado do seno te pela primeira identidade. Obtemos a soma do seno da quarta grau te do produto do cosseno quadrado te e seno quadrado te. Tiramos o fator comum seno quadrado te fora dos colchetes, entre colchetes obtemos a soma dos quadrados do cosseno e do seno, que, de acordo com a trigonométrica básica identidade, é igual a 1. Como resultado, obtemos o quadrado do seno te).
EXEMPLO 2. Simplifique a expressão: + .
(a expressão é a soma de duas frações no numerador do primeiro cosseno te no denominador um menos seno te, no numerador do segundo cosseno te no denominador do segundo mais seno te).
(Retiramos o fator comum cosseno te dos colchetes e, entre colchetes, o levamos a um denominador comum, que é o produto de um menos seno te por um mais seno te.
No numerador obtemos: um mais seno te mais um menos seno te, damos os semelhantes, o numerador é igual a dois depois de trazer os semelhantes.
No denominador, você pode aplicar a fórmula de multiplicação abreviada (diferença de quadrados) e obter a diferença entre a unidade e o quadrado do seno te, que, de acordo com a identidade trigonométrica básica
é igual ao quadrado do cosseno te. Após reduzir pelo cosseno te, obtemos a resposta final: dois dividido pelo cosseno te).
Considere exemplos do uso dessas fórmulas na demonstração de expressões trigonométricas.
EXEMPLO 3. Prove a identidade (tg 2 t - sen 2 t) ∙ ctg 2 t \u003d sen 2 t (o produto da diferença entre os quadrados da tangente de te e o seno de te e o quadrado da cotangente de te é igual ao quadrado do seno de te).
Prova.
Vamos transformar o lado esquerdo da igualdade:
(tg 2 t - sen 2 t) ∙ ctg 2 t = tg 2 t ∙ ctg 2 t - sen 2 t ∙ ctg 2 t = 1 - sen 2 t ∙ ctg 2 t =1 - sen 2 t ∙ = 1 - cos 2 t = sen 2 t
(Vamos abrir os colchetes, da relação obtida anteriormente sabe-se que o produto dos quadrados da tangente de te pela cotangente de te é igual a um. Lembre-se que a cotangente de te é igual à razão do cosseno de te ao seno de te, o que significa que o quadrado da cotangente é a razão do quadrado do cosseno de te ao quadrado do seno de te.
Após a redução pelo seno quadrado de te, obtemos a diferença entre a unidade e o cosseno do quadrado de te, que é igual ao seno do quadrado de te). Q.E.D.

EXEMPLO 4. Encontre o valor da expressão tg 2 t + ctg 2 t se tgt + ctgt = 6.
(a soma dos quadrados da tangente de te e da cotangente de te, se a soma da tangente e cotangente for seis).
Solução. (tgt + ctgt) 2 = 6 2
tg 2 t + 2 ∙ tgt ∙ctgt + ctg 2 t = 36
tg 2 t + 2 + ctg 2 t = 36
tg 2 t + ctg 2 t = 36-2
tg 2 t + ctg 2 t = 34
Vamos elevar ao quadrado ambas as partes da igualdade original:
(tgt + ctgt) 2 = 6 2 (o quadrado da soma da tangente de te e a cotangente de te é seis ao quadrado). Lembre-se da fórmula de multiplicação abreviada: O quadrado da soma de duas quantidades é igual ao quadrado da primeira mais duas vezes o produto da primeira e a segunda mais o quadrado da segunda. (a+b) 2 =a 2 +2ab+b 2 Obtemos tg 2 t + 2 ∙ tgt ∙ctgt + ctg 2 t = 36 .

Como o produto da tangente de te e a cotangente de te é igual a um, então tg 2 t + 2 + ctg 2 t \u003d 36 (a soma dos quadrados da tangente de te e a cotangente de te e dois é trinta e seis),
Voronkova Olga Ivanovna
MBOU "Ensino médio
Nº 18"
Engels, região de Saratov.
Professor de matemática.
"Expressões trigonométricas e suas transformações"
Introdução …………………………………………………………………………..3
Capítulo 1 Classificação de tarefas para o uso de transformações de expressões trigonométricas ………………………….……………………...5
1.1. Tarefas de cálculo valores de expressões trigonométricas……….5
1.2.Tarefas para simplificar expressões trigonométricas .... 7
1.3. Tarefas para a conversão de expressões trigonométricas numéricas ... ..7
1.4 Tarefas mistas……………………………………………………….9
Capítulo 2
2.1 Repetição temática no 10º ano……………………………………………11
Teste 1………………………………………………………………………………..12
Teste 2………………………………………………………………………………..13
Teste 3………………………………………………………………………………..14
2.2 Repetição final no 11º ano…………………………………………………15
Teste 1………………………………………………………………………………..17
Teste 2…………………………………………………………………………………..17
Teste 3…………………………………………………………………………………..18
Conclusão.…………………………………………………………………………19
Lista de literatura usada…………………………………………..…….20
Introdução.
Nas condições de hoje, a pergunta mais importante é: "Como podemos ajudar a eliminar algumas lacunas no conhecimento dos alunos e alertá-los contra possíveis erros no exame?" Para resolver esta questão, é necessário conseguir dos alunos não uma assimilação formal do material do programa, mas a sua compreensão profunda e consciente, o desenvolvimento da velocidade de cálculos e transformações orais, bem como o desenvolvimento de habilidades para resolver os mais simples problemas “na mente”. É necessário convencer os alunos de que somente na presença de um cargo ativo, no estudo da matemática, sujeito à aquisição de habilidades práticas e seu uso, pode-se contar com um verdadeiro sucesso. É necessário aproveitar todas as oportunidades de preparação para o exame, incluindo disciplinas eletivas nas séries 10-11, para analisar regularmente tarefas complexas com os alunos, escolhendo a maneira mais racional de resolvê-las em sala de aula e aulas extras.resultado positivo ema área de resolução de problemas típicos pode ser alcançada se os professores de matemática, criandoboa formação básica dos alunos, procurar novos caminhos para resolver os problemas que se abriram diante de nós, experimentar ativamente, aplicar tecnologias pedagógicas modernas, métodos, técnicas que criem condições favoráveis para a auto-realização e autodeterminação efetiva dos alunos em novas condições sociais.
A trigonometria é parte integrante do curso de matemática escolar. Bons conhecimentos e fortes habilidades em trigonometria são evidências de um nível suficiente de cultura matemática, uma condição indispensável para o estudo bem-sucedido de matemática, física e uma série de técnicas disciplinas.
A relevância do trabalho. Uma parte significativa dos graduados do ensino médio mostra de ano para ano uma preparação muito ruim nesta importante seção da matemática, como evidenciado pelos resultados dos anos anteriores (porcentagem de conclusão em 2011-48,41%, 2012-51,05%), desde a análise de aprovação o exame estadual unificado mostrou que os alunos cometem muitos erros ao completar tarefas desta seção em particular ou não realizam tais tarefas. Em um As questões do exame estadual em trigonometria são encontradas em quase três tipos de tarefas. Esta é a solução das equações trigonométricas mais simples na tarefa B5, e trabalhar com expressões trigonométricas na tarefa B7, e o estudo de funções trigonométricas na tarefa B14, bem como tarefas B12, nas quais existem fórmulas descrevendo fenômenos físicos e contendo funções trigonométricas . E isso é apenas parte das tarefas B! Mas também existem equações trigonométricas favoritas com a seleção de raízes C1 e tarefas geométricas “não muito favoritas” C2 e C4.
Objetivo. Analisar o material das tarefas USE B7, dedicadas à transformação de expressões trigonométricas e classificar as tarefas de acordo com a forma de apresentação nas provas.
O trabalho é composto por dois capítulos, introdução e conclusão. A introdução enfatiza a relevância do trabalho. O primeiro capítulo fornece uma classificação de tarefas para o uso de transformações de expressões trigonométricas nas tarefas de teste do Unified State Examination (2012).
No segundo capítulo, é considerada a organização da repetição do tópico "Transformação de expressões trigonométricas" nas classes 10, 11 e são desenvolvidos testes sobre este tópico.
A lista de referências inclui 17 fontes.
Capítulo 1. Classificação de tarefas para o uso de transformações de expressões trigonométricas.
De acordo com o padrão do ensino médio (completo) e os requisitos para o nível de treinamento dos alunos, as tarefas para o conhecimento dos fundamentos da trigonometria estão incluídas no codificador de requisitos.
Aprender o básico da trigonometria será mais eficaz quando:
os alunos serão positivamente motivados a repetir o material estudado anteriormente;
uma abordagem centrada no aluno será implementada no processo educacional;
será aplicado um sistema de tarefas que contribua para a ampliação, aprofundamento, sistematização dos conhecimentos dos alunos;
tecnologias pedagógicas avançadas serão utilizadas.
Depois de analisar a literatura e os recursos da Internet para a preparação para o exame, propusemos uma das possíveis classificações das tarefas B7 (KIM USE 2012-trigonometria): tarefas para calcularvalores de expressões trigonométricas; atribuições paraconversão de expressões trigonométricas numéricas; atribuições para a transformação de expressões trigonométricas literais; tarefas mistas.
1.1. Tarefas de cálculo valores de expressões trigonométricas.
Um dos tipos mais comuns de problemas de trigonometria simples é o cálculo dos valores das funções trigonométricas pelo valor de uma delas:
a) Uso da identidade trigonométrica básica e seus corolários.
Exemplo 1
. Encontre se  e
e  .
.
Solução.  ,
,  ,
,
Porque , então  .
.
Responda.
Exemplo 2
. Achar  , E se
, E se  e .
e .
Solução.  ,
,  ,
,  .
.
Porque , então  .
.
Responda. .
b) Uso de fórmulas de duplo ângulo.
Exemplo 3
. Achar  , E se
, E se  .
.
Solução. ,  .
.
Responda.  .
.
Exemplo 4
. Encontrar o valor de uma expressão  .
.
Solução. .
Responda.  .
.
1. Achar , E se
 e
e  . Responda. -0,2
. Responda. -0,2 2.
Achar , E se  e
e  . Responda. 0,4
. Responda. 0,4
 , E se . Responda. -12,884.
Achar
, E se . Responda. -12,884.
Achar  , E se
, E se  . Responda. -0,845.
Encontre o valor da expressão:
. Responda. -0,845.
Encontre o valor da expressão: . Responda. 66.
Encontrar o valor de uma expressão
. Responda. 66.
Encontrar o valor de uma expressão .Responda. -19
.Responda. -191.2.Tarefas para simplificar expressões trigonométricas. As fórmulas de redução devem ser bem dominadas pelos alunos, pois serão posteriormente utilizadas nas aulas de geometria, física e outras disciplinas afins.
Exemplo 5
.
Simplifique expressões  .
.
Solução. .
Responda.  .
.
Tarefas para solução independente:
1. Simplifique a expressão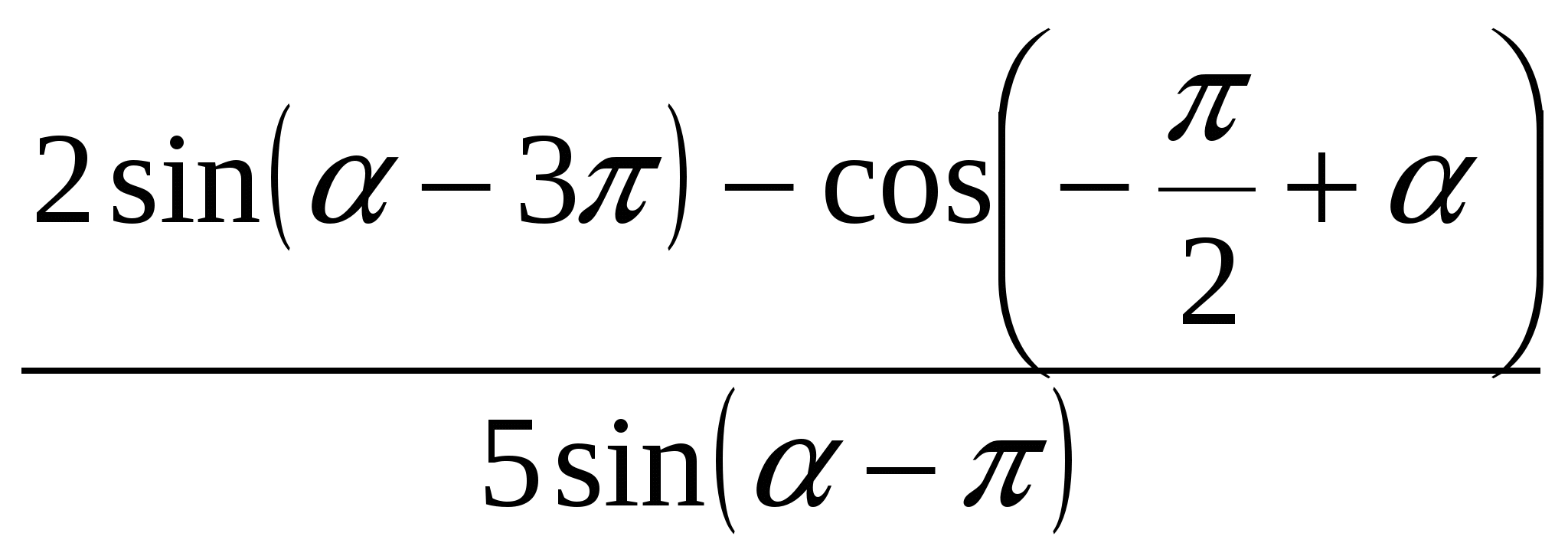 .
Responda. 0,62.
Achar
.
Responda. 0,62.
Achar  , E se
, E se  e. Responda. 10,563.
Encontrar o valor de uma expressão
e. Responda. 10,563.
Encontrar o valor de uma expressão  , E se
, E se  .
Responda. 2
.
Responda. 2 1.3. Tarefas para a transformação de expressões trigonométricas numéricas.
Ao desenvolver as habilidades e habilidades de tarefas para converter expressões trigonométricas numéricas, deve-se prestar atenção ao conhecimento da tabela de valores das funções trigonométricas, as propriedades de paridade e periodicidade das funções trigonométricas.
a) Usando valores exatos de funções trigonométricas para alguns ângulos.
Exemplo 6
. Calcular  .
.
Solução.  .
.
Responda.  .
.
b) Usando as propriedades da paridade funções trigonométricas.
Exemplo 7
. Calcular  .
.
Solução. .
Responda. 
dentro) Usando Propriedades de Periodicidadefunções trigonométricas.
Exemplo 8
.
Encontrar o valor de uma expressão  .
.
Solução. .
Responda.  .
.
Tarefas para solução independente:
1. Encontrar o valor de uma expressão .
Responda. -40,52. Encontre o valor da expressão
.
Responda. -40,52. Encontre o valor da expressão  .
Responda. 17
.
Responda. 17 3.
Encontrar o valor de uma expressão  .
Responda. 6
.
Responda. 6
 .
Responda. -24
.
Responda. -24  Responda. -64
Responda. -641.4 Tarefas mistas.
A forma de teste de certificação possui características muito significativas, por isso é importante prestar atenção às tarefas associadas ao uso de várias fórmulas trigonométricas ao mesmo tempo.
Exemplo 9
Achar  , E se
, E se  .
.
Solução.  .
.
Responda.  .
.
Exemplo 10
. Achar  , E se
, E se  e
e  .
.
Solução. .
Porque , então  .
.
Responda.  .
.
Exemplo 11.
Achar  , E se .
, E se .
Solução. , ,  ,
,  ,
,  ,
,  ,
,  .
.
Responda.
Exemplo 12.
Calcular  .
.
Solução. .
Responda.  .
.
Exemplo 13
Encontrar o valor de uma expressão  , E se
, E se  .
.
Solução. .
Responda.  .
.
Tarefas para solução independente:
1. Achar , E se
, E se  .
Responda. -1,75
.
Responda. -1,752. Achar
 , E se
, E se  .
Responda. 33. Encontre
.
Responda. 33. Encontre  , E se .Responda. 0,254. Encontre o valor da expressão
, E se .Responda. 0,254. Encontre o valor da expressão  , E se
, E se  .
Responda. 0,35. Encontre o valor da expressão
.
Responda. 0,35. Encontre o valor da expressão  , E se
, E se  .
Responda. 5
.
Responda. 5Capítulo 2. Organização dos aspectos metodológicos da repetição final do tópico "Transformação de expressões trigonométricas".
Uma das questões mais importantes que contribuem para a melhoria ainda maior do desempenho acadêmico, a conquista de conhecimentos profundos e sólidos entre os alunos é a questão da repetição de material previamente estudado. A prática mostra que no 10º ano é mais conveniente organizar uma repetição temática; no 11º ano - a repetição final.
2.1. Repetição temática no 10º ano.
No processo de trabalhar em material matemático, a repetição de cada tópico concluído ou de uma seção inteira do curso torna-se especialmente importante.
Com a repetição temática, o conhecimento dos alunos sobre o tema é sistematizado na fase final de sua passagem ou após um intervalo.
Para a repetição temática, são alocadas aulas especiais, nas quais o material de um determinado tópico é concentrado e generalizado.
A repetição na aula é realizada através de uma conversa com o amplo envolvimento dos alunos nessa conversa. Depois disso, os alunos recebem a tarefa de repetir um determinado tópico e são avisados de que haverá trabalho de crédito nos testes.
Um teste sobre um tópico deve incluir todas as suas questões principais. Após a conclusão do trabalho, os erros característicos são analisados e uma repetição é organizada para eliminá-los.
Para aulas de repetição temática, oferecemos papéis de teste sobre o tema "Conversão de expressões trigonométricas".
Teste nº 1
Teste nº 2
Teste nº 3
Tabela de respostas
Teste
2.2. Repetição final no 11º ano.
A repetição final é realizada na fase final do estudo das principais questões do curso de matemática e é realizada em conexão lógica com o estudo do material didático para esta seção ou o curso como um todo.
A repetição final do material educativo tem os seguintes objetivos:
1. Ativação do material de todo o curso de treinamento para esclarecer sua estrutura lógica e construir um sistema dentro das relações disciplinares e interdisciplinares.
2. Aprofundar e, se possível, ampliar o conhecimento dos alunos sobre as principais questões do curso em processo de repetência.
No âmbito do exame obrigatório de matemática para todos os licenciados, a introdução gradual do USE faz com que os professores assumam uma nova abordagem na preparação e condução das aulas, tendo em conta a necessidade de garantir que todos os alunos dominem o material didáctico ao nível básico, bem como a oportunidade para estudantes motivados interessados em obter altas pontuações para admissão em uma universidade, avanço dinâmico no domínio do material em um nível avançado e alto.
Nas lições da repetição final, você pode considerar as seguintes tarefas:
Exemplo 1 . Calcule o valor da expressão.Solução. = = =
= =  =
= =
= =
= =0,5.
Responda. 0,5. Exemplo 2
Especifique o maior valor inteiro que a expressão pode assumir
=0,5.
Responda. 0,5. Exemplo 2
Especifique o maior valor inteiro que a expressão pode assumir  .
.
Solução. Porque  pode assumir qualquer valor pertencente ao segmento [–1; 1], então
pode assumir qualquer valor pertencente ao segmento [–1; 1], então  assume qualquer valor do segmento [–0,4; 0,4], portanto. O valor inteiro da expressão é um - o número 4.
assume qualquer valor do segmento [–0,4; 0,4], portanto. O valor inteiro da expressão é um - o número 4.
 .
.
Solução: Vamos usar a fórmula para fatorar a soma dos cubos: . Nós temos
Nós temos:  .
.
Resposta 1
Exemplo 4
Calcular  .
.
Solução. .
Resposta: 0,28
Para as aulas de repetição final, oferecemos testes desenvolvidos sobre o tema "Conversão de expressões trigonométricas".
Especifique o maior inteiro que não exceda 1
Conclusão.
Tendo trabalhado na literatura metodológica relevante sobre este tópico, podemos concluir que a capacidade e as habilidades para resolver tarefas relacionadas a transformações trigonométricas no curso de matemática escolar são muito importantes.
No decorrer do trabalho realizado, foi realizada a classificação das tarefas B7. São consideradas as fórmulas trigonométricas mais utilizadas nas CMMs de 2012. São dados exemplos de tarefas com soluções. Testes diferenciáveis foram desenvolvidos para organizar a repetição e sistematização do conhecimento em preparação para o exame.
É aconselhável continuar o trabalho iniciado, considerando solução das equações trigonométricas mais simples na tarefa B5, o estudo de funções trigonométricas na tarefa B14, tarefa B12, na qual existem fórmulas descrevendo fenômenos físicos e contendo funções trigonométricas.
Para concluir, gostaria de observar que a eficácia da aprovação no exame é amplamente determinada pela eficácia com que o processo de preparação é organizado em todos os níveis de ensino, com todas as categorias de alunos. E se conseguirmos formar nos alunos a independência, a responsabilidade e a prontidão para continuar aprendendo ao longo de suas vidas subsequentes, não apenas cumpriremos a ordem do Estado e da sociedade, mas também aumentaremos nossa própria auto-estima.
A repetição de material didático exige um trabalho criativo do professor. Ele deve fornecer uma conexão clara entre os tipos de repetição, implementar um sistema de repetição profundamente pensado. Dominar a arte de organizar a repetição é tarefa do professor. A força do conhecimento dos alunos depende em grande parte de sua solução.
Literatura.
Vygodsky Ya.Ya., Manual de matemática elementar. -M.: Nauka, 1970.
Tarefas de dificuldade aumentada em álgebra e os primórdios da análise: livro didático para 10-11 anos do ensino médio / B.M. Ivlev, A. M. Abramov, Yu.P. Dudnitsyn, S.I. Schwarzburd. – M.: Iluminismo, 1990.
Aplicação de fórmulas trigonométricas básicas à transformação de expressões (10º ano) // Festival de Ideias Pedagógicas. 2012-2013.
Koryanov A. G. , Prokofiev A.A. Preparamos bons alunos e excelentes alunos para o exame. - M.: Universidade Pedagógica "Primeiro de Setembro", 2012.- 103 p.
Kuznetsova E. N. Simplificação de expressões trigonométricas. Resolução de equações trigonométricas por vários métodos (preparação para o exame). 11 º ano. 2012-2013.
Kulanin E.D. 3000 problemas competitivos em matemática. 4º id., correto. e adicional – M.: Rolf, 2000.
Mordkovitch A. G. Problemas metódicos do estudo da trigonometria em uma escola de ensino geral // Matemática na escola. 2002. Nº 6.
Pichurin L. F. Sobre trigonometria e não só sobre ela: -M. Iluminismo, 1985
Reshetnikov N.N. Trigonometria na escola: -M. : Universidade Pedagógica "Primeiro de Setembro", 2006, lk 1.
Shabunin M.I., Prokofiev A.A. Matemáticas. Álgebra. Princípios da análise matemática Nível de perfil: livro didático para 10ª série - M .: BINOM. Laboratório do Conhecimento, 2007.
Portal educacional para se preparar para o exame.
Preparando-se para o exame de matemática "Ah, essa trigonometria! http://festival.1september.ru/articles/621971/
Projeto "Matemática? Fácil!!!" http://www.resolventa.ru/
Seções: Matemáticas
Classe: 11
Lição 1
Tema: 11º ano (preparação para o exame)
Simplificação de expressões trigonométricas.
Solução das equações trigonométricas mais simples. (2 horas)
Metas:
- Sistematizar, generalizar, ampliar os conhecimentos e habilidades dos alunos relacionados ao uso de fórmulas trigonométricas e à solução das equações trigonométricas mais simples.
Equipamento para a aula:
Estrutura da lição:
- Orgmoment
- Testes em laptops. A discussão dos resultados.
- Simplificando expressões trigonométricas
- Solução das equações trigonométricas mais simples
- Trabalho independente.
- Resumo da lição. Explicação do dever de casa.
1. Momento organizador. (2 minutos.)
O professor cumprimenta a plateia, anuncia o tema da aula, lembra que antes foi dada a tarefa de repetir as fórmulas de trigonometria e prepara os alunos para a prova.
2. Teste. (15min + 3min de discussão)
O objetivo é testar o conhecimento de fórmulas trigonométricas e a capacidade de aplicá-las. Cada aluno tem um laptop em sua mesa no qual há uma opção de teste.
Pode haver qualquer número de opções, vou dar um exemplo de uma delas:
eu opção.
Simplifique as expressões:
a) identidades trigonométricas básicas
1. sin 2 3y + cos 2 3y + 1;
b) fórmulas de adição
3. sen5x - sen3x;
c) converter um produto em uma soma
6. 2sin8y cos3y;
d) fórmulas de ângulo duplo
7,2sin5x cos5x;
e) fórmulas de meio ângulo
f) fórmulas de ângulo triplo
g) substituição universal
h) abaixando o grau
16. cos 2 (3x/7);
Os alunos em um laptop na frente de cada fórmula veem suas respostas.
O trabalho é instantaneamente verificado pelo computador. Os resultados são exibidos em uma tela grande para que todos possam ver.
Além disso, após o término do trabalho, as respostas corretas são mostradas nos laptops dos alunos. Cada aluno vê onde o erro foi cometido e quais fórmulas ele precisa repetir.
3. Simplificação de expressões trigonométricas. (25 minutos)
O objetivo é repetir, trabalhar e consolidar a aplicação das fórmulas básicas da trigonometria. Resolvendo problemas B7 do exame.
Nesta fase, é aconselhável dividir a turma em grupos de alunos fortes (trabalhar de forma independente com posterior verificação) e alunos fracos que trabalham com o professor.
Tarefa para alunos fortes (preparada com antecedência em uma base impressa). A ênfase principal está nas fórmulas de redução e duplo ângulo, de acordo com o USE 2011.
Simplifique expressões (para aprendizes fortes):

Em paralelo, o professor trabalha com alunos fracos, discutindo e resolvendo tarefas na tela sob o ditado dos alunos.
Calcular:
5) sin(270º - α) + cos(270º + α)
6) 
Simplificar:

Foi a vez de discutir os resultados do trabalho do grupo forte.
As respostas aparecem na tela e também, com a ajuda de uma câmera de vídeo, são exibidos os trabalhos de 5 alunos diferentes (uma tarefa para cada).
O grupo fraco vê a condição e o método de solução. Há discussão e análise. Com o uso de meios técnicos, isso acontece rapidamente.
4. Solução das equações trigonométricas mais simples. (30 minutos.)
O objetivo é repetir, sistematizar e generalizar a solução das equações trigonométricas mais simples, registrando suas raízes. Solução do problema B3.
Qualquer equação trigonométrica, não importa como a resolvamos, leva à mais simples.
Ao completar a tarefa, os alunos devem prestar atenção à escrita das raízes das equações de casos particulares e forma geral e à seleção de raízes na última equação.
Resolva as equações:

Escreva a menor raiz positiva da resposta.
5. Trabalho independente (10 min.)
O objetivo é testar as habilidades adquiridas, identificar problemas, erros e formas de eliminá-los.
Uma variedade de trabalhos é oferecida à escolha do aluno.
Opção para "3"
1) Encontre o valor da expressão ![]()
2) Simplifique a expressão 1 - sin 2 3α - cos 2 3α
3) Resolva a equação ![]()
Opção para "4"
1) Encontre o valor da expressão
2) Resolva a equação ![]() Escreva a menor raiz positiva de sua resposta.
Escreva a menor raiz positiva de sua resposta.
Opção para "5"
1) Encontre tgα se ![]()
2) Encontre a raiz da equação ![]() Escreva a menor raiz positiva de sua resposta.
Escreva a menor raiz positiva de sua resposta.
6. Resumo da lição (5 min.)
O professor resume o fato de que a aula repetiu e consolidou fórmulas trigonométricas, a solução das equações trigonométricas mais simples.
A lição de casa é atribuída (preparada em uma base impressa com antecedência) com uma verificação pontual na próxima lição.
Resolva as equações:

9) ![]()
10) ![]() Dê sua resposta como a menor raiz positiva.
Dê sua resposta como a menor raiz positiva.
Lição 2
Tema: 11º ano (preparação para o exame)
Métodos de resolução de equações trigonométricas. Seleção de raiz. (2 horas)
Metas:
- Generalizar e sistematizar conhecimentos sobre a resolução de equações trigonométricas de vários tipos.
- Para promover o desenvolvimento do pensamento matemático dos alunos, a capacidade de observar, comparar, generalizar, classificar.
- Incentivar os alunos a superar as dificuldades no processo de atividade mental, ao autocontrole, à introspecção de suas atividades.
Equipamento para a aula: KRMu, laptops para cada aluno.
Estrutura da lição:
- Orgmoment
- Discussão d / se samot. o trabalho da última aula
- Repetição de métodos de resolução de equações trigonométricas.
- Resolvendo equações trigonométricas
- Seleção de raízes em equações trigonométricas.
- Trabalho independente.
- Resumo da lição. Trabalho de casa.
1. Momento de organização (2 min.)
O professor cumprimenta o público, anuncia o tema da aula e o plano de trabalho.
2. a) Análise do dever de casa (5 min.)
O objetivo é verificar o desempenho. Um trabalho com a ajuda de uma câmera de vídeo é exibido na tela, o restante é coletado seletivamente para o professor conferir.
b) Análise de trabalho independente (3 min.)
O objetivo é resolver os erros, indicar formas de superá-los.
Na tela estão as respostas e soluções, os alunos já emitiram seus trabalhos. A análise está indo rápido.
3. Repetição de métodos para resolver equações trigonométricas (5 min.)
O objetivo é relembrar métodos para resolver equações trigonométricas.
Pergunte aos alunos quais métodos de resolução de equações trigonométricas eles conhecem. Enfatize que existem os chamados métodos básicos (frequentemente usados):
- substituição variável,
- fatoração,
- equações homogêneas,
e existem métodos aplicados:
- de acordo com as fórmulas para converter uma soma em um produto e um produto em uma soma,
- pelas fórmulas de redução,
- substituição trigonométrica universal
- introdução de um ângulo auxiliar,
- multiplicação por alguma função trigonométrica.
Também deve ser lembrado que uma equação pode ser resolvida de maneiras diferentes.
4. Resolvendo equações trigonométricas (30 min.)
O objetivo é generalizar e consolidar conhecimentos e habilidades sobre este tema, para preparar para a resolução de C1 a partir do USE.
Considero conveniente resolver equações para cada método em conjunto com os alunos.
O aluno dita a solução, o professor anota no tablet, todo o processo é exibido na tela. Isso permitirá que você restaure de forma rápida e eficiente o material anteriormente coberto em sua memória.
Resolva as equações:
1) mudança de variável 6cos 2 x + 5sinx - 7 = 0
2) fatoração 3cos(x/3) + 4cos 2 (x/3) = 0
3) equações homogêneas sen 2 x + 3cos 2 x - 2sen2x = 0
4) convertendo a soma no produto cos5x + cos7x = cos(π + 6x)
5) convertendo o produto na soma 2sinx sen2x + cos3x = 0
6) diminuindo o grau de sin2x - sin 2 2x + sin 2 3x \u003d 0,5
7) substituição trigonométrica universal senx + 5cosx + 5 = 0.
Ao resolver esta equação, deve-se notar que o uso deste método leva a um estreitamento do domínio de definição, uma vez que o seno e o cosseno são substituídos por tg(x/2). Portanto, antes de escrever a resposta, é necessário verificar se os números do conjunto π + 2πn, n Z são cavalos desta equação.
8) introdução de um ângulo auxiliar √3sinx + cosx - √2 = 0
9) multiplicação por alguma função trigonométrica cosx cos2x cos4x = 1/8.
5. Seleção de raízes de equações trigonométricas (20 min.)
Como nas condições de acirrada competição ao ingressar nas universidades, a solução de uma primeira parte do exame não é suficiente, a maioria dos alunos deve prestar atenção às tarefas da segunda parte (C1, C2, C3).
Portanto, o objetivo desta etapa da aula é relembrar o material estudado anteriormente, para se preparar para a resolução do problema C1 do USE em 2011.
Existem equações trigonométricas nas quais você precisa selecionar as raízes ao escrever a resposta. Isso se deve a algumas restrições, por exemplo: o denominador de uma fração não é igual a zero, a expressão sob a raiz de um grau par é não negativa, a expressão sob o sinal do logaritmo é positiva, etc.
Tais equações são consideradas equações de complexidade aumentada e na versão USE estão na segunda parte, a saber C1.
Resolva a equação:
A fração é zero se então ![]() usando o círculo unitário, vamos selecionar as raízes (veja a Figura 1)
usando o círculo unitário, vamos selecionar as raízes (veja a Figura 1)

Imagem 1.
obtemos x = π + 2πn, n Z
Resposta: π + 2πn, n Z
Na tela, a seleção de raízes é mostrada em um círculo em uma imagem colorida.
O produto é igual a zero quando pelo menos um dos fatores é igual a zero, e o arco, ao mesmo tempo, não perde seu significado. Então

Usando o círculo unitário, selecione as raízes (veja a Figura 2)

Seções: Matemáticas
Classe: 11
Lição 1
Tema: 11º ano (preparação para o exame)
Simplificação de expressões trigonométricas.
Solução das equações trigonométricas mais simples. (2 horas)
Metas:
- Sistematizar, generalizar, ampliar os conhecimentos e habilidades dos alunos relacionados ao uso de fórmulas trigonométricas e à solução das equações trigonométricas mais simples.
Equipamento para a aula:
Estrutura da lição:
- Orgmoment
- Testes em laptops. A discussão dos resultados.
- Simplificando expressões trigonométricas
- Solução das equações trigonométricas mais simples
- Trabalho independente.
- Resumo da lição. Explicação do dever de casa.
1. Momento organizador. (2 minutos.)
O professor cumprimenta a plateia, anuncia o tema da aula, lembra que antes foi dada a tarefa de repetir as fórmulas de trigonometria e prepara os alunos para a prova.
2. Teste. (15min + 3min de discussão)
O objetivo é testar o conhecimento de fórmulas trigonométricas e a capacidade de aplicá-las. Cada aluno tem um laptop em sua mesa no qual há uma opção de teste.
Pode haver qualquer número de opções, vou dar um exemplo de uma delas:
eu opção.
Simplifique as expressões:
a) identidades trigonométricas básicas
1. sin 2 3y + cos 2 3y + 1;
b) fórmulas de adição
3. sen5x - sen3x;
c) converter um produto em uma soma
6. 2sin8y cos3y;
d) fórmulas de ângulo duplo
7,2sin5x cos5x;
e) fórmulas de meio ângulo
f) fórmulas de ângulo triplo
g) substituição universal
h) abaixando o grau
16. cos 2 (3x/7);
Os alunos em um laptop na frente de cada fórmula veem suas respostas.
O trabalho é instantaneamente verificado pelo computador. Os resultados são exibidos em uma tela grande para que todos possam ver.
Além disso, após o término do trabalho, as respostas corretas são mostradas nos laptops dos alunos. Cada aluno vê onde o erro foi cometido e quais fórmulas ele precisa repetir.
3. Simplificação de expressões trigonométricas. (25 minutos)
O objetivo é repetir, trabalhar e consolidar a aplicação das fórmulas básicas da trigonometria. Resolvendo problemas B7 do exame.
Nesta fase, é aconselhável dividir a turma em grupos de alunos fortes (trabalhar de forma independente com posterior verificação) e alunos fracos que trabalham com o professor.
Tarefa para alunos fortes (preparada com antecedência em uma base impressa). A ênfase principal está nas fórmulas de redução e duplo ângulo, de acordo com o USE 2011.
Simplifique expressões (para aprendizes fortes):

Em paralelo, o professor trabalha com alunos fracos, discutindo e resolvendo tarefas na tela sob o ditado dos alunos.
Calcular:
5) sin(270º - α) + cos(270º + α)
6) 
Simplificar:

Foi a vez de discutir os resultados do trabalho do grupo forte.
As respostas aparecem na tela e também, com a ajuda de uma câmera de vídeo, são exibidos os trabalhos de 5 alunos diferentes (uma tarefa para cada).
O grupo fraco vê a condição e o método de solução. Há discussão e análise. Com o uso de meios técnicos, isso acontece rapidamente.
4. Solução das equações trigonométricas mais simples. (30 minutos.)
O objetivo é repetir, sistematizar e generalizar a solução das equações trigonométricas mais simples, registrando suas raízes. Solução do problema B3.
Qualquer equação trigonométrica, não importa como a resolvamos, leva à mais simples.
Ao completar a tarefa, os alunos devem prestar atenção à escrita das raízes das equações de casos particulares e forma geral e à seleção de raízes na última equação.
Resolva as equações:

Escreva a menor raiz positiva da resposta.
5. Trabalho independente (10 min.)
O objetivo é testar as habilidades adquiridas, identificar problemas, erros e formas de eliminá-los.
Uma variedade de trabalhos é oferecida à escolha do aluno.
Opção para "3"
1) Encontre o valor da expressão ![]()
2) Simplifique a expressão 1 - sin 2 3α - cos 2 3α
3) Resolva a equação ![]()
Opção para "4"
1) Encontre o valor da expressão
2) Resolva a equação ![]() Escreva a menor raiz positiva de sua resposta.
Escreva a menor raiz positiva de sua resposta.
Opção para "5"
1) Encontre tgα se ![]()
2) Encontre a raiz da equação ![]() Escreva a menor raiz positiva de sua resposta.
Escreva a menor raiz positiva de sua resposta.
6. Resumo da lição (5 min.)
O professor resume o fato de que a aula repetiu e consolidou fórmulas trigonométricas, a solução das equações trigonométricas mais simples.
A lição de casa é atribuída (preparada em uma base impressa com antecedência) com uma verificação pontual na próxima lição.
Resolva as equações:

9) ![]()
10) ![]() Dê sua resposta como a menor raiz positiva.
Dê sua resposta como a menor raiz positiva.
Lição 2
Tema: 11º ano (preparação para o exame)
Métodos de resolução de equações trigonométricas. Seleção de raiz. (2 horas)
Metas:
- Generalizar e sistematizar conhecimentos sobre a resolução de equações trigonométricas de vários tipos.
- Para promover o desenvolvimento do pensamento matemático dos alunos, a capacidade de observar, comparar, generalizar, classificar.
- Incentivar os alunos a superar as dificuldades no processo de atividade mental, ao autocontrole, à introspecção de suas atividades.
Equipamento para a aula: KRMu, laptops para cada aluno.
Estrutura da lição:
- Orgmoment
- Discussão d / se samot. o trabalho da última aula
- Repetição de métodos de resolução de equações trigonométricas.
- Resolvendo equações trigonométricas
- Seleção de raízes em equações trigonométricas.
- Trabalho independente.
- Resumo da lição. Trabalho de casa.
1. Momento de organização (2 min.)
O professor cumprimenta o público, anuncia o tema da aula e o plano de trabalho.
2. a) Análise do dever de casa (5 min.)
O objetivo é verificar o desempenho. Um trabalho com a ajuda de uma câmera de vídeo é exibido na tela, o restante é coletado seletivamente para o professor conferir.
b) Análise de trabalho independente (3 min.)
O objetivo é resolver os erros, indicar formas de superá-los.
Na tela estão as respostas e soluções, os alunos já emitiram seus trabalhos. A análise está indo rápido.
3. Repetição de métodos para resolver equações trigonométricas (5 min.)
O objetivo é relembrar métodos para resolver equações trigonométricas.
Pergunte aos alunos quais métodos de resolução de equações trigonométricas eles conhecem. Enfatize que existem os chamados métodos básicos (frequentemente usados):
- substituição variável,
- fatoração,
- equações homogêneas,
e existem métodos aplicados:
- de acordo com as fórmulas para converter uma soma em um produto e um produto em uma soma,
- pelas fórmulas de redução,
- substituição trigonométrica universal
- introdução de um ângulo auxiliar,
- multiplicação por alguma função trigonométrica.
Também deve ser lembrado que uma equação pode ser resolvida de maneiras diferentes.
4. Resolvendo equações trigonométricas (30 min.)
O objetivo é generalizar e consolidar conhecimentos e habilidades sobre este tema, para preparar para a resolução de C1 a partir do USE.
Considero conveniente resolver equações para cada método em conjunto com os alunos.
O aluno dita a solução, o professor anota no tablet, todo o processo é exibido na tela. Isso permitirá que você restaure de forma rápida e eficiente o material anteriormente coberto em sua memória.
Resolva as equações:
1) mudança de variável 6cos 2 x + 5sinx - 7 = 0
2) fatoração 3cos(x/3) + 4cos 2 (x/3) = 0
3) equações homogêneas sen 2 x + 3cos 2 x - 2sen2x = 0
4) convertendo a soma no produto cos5x + cos7x = cos(π + 6x)
5) convertendo o produto na soma 2sinx sen2x + cos3x = 0
6) diminuindo o grau de sin2x - sin 2 2x + sin 2 3x \u003d 0,5
7) substituição trigonométrica universal senx + 5cosx + 5 = 0.
Ao resolver esta equação, deve-se notar que o uso deste método leva a um estreitamento do domínio de definição, uma vez que o seno e o cosseno são substituídos por tg(x/2). Portanto, antes de escrever a resposta, é necessário verificar se os números do conjunto π + 2πn, n Z são cavalos desta equação.
8) introdução de um ângulo auxiliar √3sinx + cosx - √2 = 0
9) multiplicação por alguma função trigonométrica cosx cos2x cos4x = 1/8.
5. Seleção de raízes de equações trigonométricas (20 min.)
Como nas condições de acirrada competição ao ingressar nas universidades, a solução de uma primeira parte do exame não é suficiente, a maioria dos alunos deve prestar atenção às tarefas da segunda parte (C1, C2, C3).
Portanto, o objetivo desta etapa da aula é relembrar o material estudado anteriormente, para se preparar para a resolução do problema C1 do USE em 2011.
Existem equações trigonométricas nas quais você precisa selecionar as raízes ao escrever a resposta. Isso se deve a algumas restrições, por exemplo: o denominador de uma fração não é igual a zero, a expressão sob a raiz de um grau par é não negativa, a expressão sob o sinal do logaritmo é positiva, etc.
Tais equações são consideradas equações de complexidade aumentada e na versão USE estão na segunda parte, a saber C1.
Resolva a equação:
A fração é zero se então ![]() usando o círculo unitário, vamos selecionar as raízes (veja a Figura 1)
usando o círculo unitário, vamos selecionar as raízes (veja a Figura 1)

Imagem 1.
obtemos x = π + 2πn, n Z
Resposta: π + 2πn, n Z
Na tela, a seleção de raízes é mostrada em um círculo em uma imagem colorida.
O produto é igual a zero quando pelo menos um dos fatores é igual a zero, e o arco, ao mesmo tempo, não perde seu significado. Então

Usando o círculo unitário, selecione as raízes (veja a Figura 2)

Figura 2.
5) ![]()
Vamos ao sistema:
![]()
Na primeira equação do sistema, fazemos a mudança log 2 (senx) = y, obtemos a equação então ![]() , de volta ao sistema
, de volta ao sistema
usando o círculo unitário, selecionamos as raízes (veja a Figura 5),

Figura 5

6. Trabalho independente (15 min.)
O objetivo é consolidar e verificar a assimilação do material, identificar erros e traçar formas de corrigi-los.
A obra é oferecida em três versões, preparadas previamente em formato impresso, à escolha dos alunos.
As equações podem ser resolvidas de qualquer maneira.
Opção para "3"
Resolva as equações:
1) 2sen 2 x + senx - 1 = 0
2) sen2x = √3cosx
Opção para "4"
Resolva as equações:
1) cos2x = 11sinx - 5
2) (2sinx + √3)log 8 (cosx) = 0
Opção para "5"
Resolva as equações:
1) 2sinx - 3cosx = 2
2) ![]()
7. Resumo da lição, dever de casa (5 min.)
O professor resume a aula, mais uma vez chama a atenção para o fato de que a equação trigonométrica pode ser resolvida de diversas formas. A melhor maneira de alcançar um resultado rápido é aquela que é melhor aprendida por um determinado aluno.
Ao se preparar para o exame, você precisa repetir sistematicamente as fórmulas e métodos para resolver equações.
Os trabalhos de casa (preparados com antecedência numa base impressa) são distribuídos e as formas de resolver algumas equações são comentadas.
Resolva as equações:
1) cosx + cos5x = cos3x + cos7x
2) 5sen(x/6) - cos(x/3) + 3 = 0
3) 4sen 2x + sen2x = 3
4) sen 2 x + sen 2 2x - sen 2 3x - sen 2 4x = 0
5) cos3x cos6x = cos4x cos7x
6) 4sinx - 6cosx = 1
7) 3sen2x + 4 cos2x = 5
8) cosx cos2x cos4x cos8x = (1/8) cos15x
9) (2sin 2 x - sinx)log 3 (2cos 2 x + cosx) = 0
10) (2cos 2 x - √3cosx)log 7 (-tgx) = 0
11) ![]()
NO transformações idênticas expressões trigonométricas os seguintes truques algébricos podem ser usados: adição e subtração de termos idênticos; tirando o fator comum entre colchetes; multiplicação e divisão pelo mesmo valor; aplicação de fórmulas de multiplicação abreviadas; seleção de um quadrado completo; fatoração de um trinômio quadrado; introdução de novas variáveis para simplificar as transformações.
Ao converter expressões trigonométricas contendo frações, você pode usar as propriedades de proporção, redução de frações ou redução de frações para um denominador comum. Além disso, você pode usar a seleção da parte inteira da fração, multiplicando o numerador e o denominador da fração pelo mesmo valor, e também, se possível, levar em consideração a uniformidade do numerador ou denominador. Se necessário, você pode representar uma fração como uma soma ou diferença de várias frações mais simples.
Além disso, ao aplicar todos os métodos necessários para converter expressões trigonométricas, é necessário levar em consideração constantemente o intervalo de valores permitidos das expressões convertidas.
Vejamos alguns exemplos.
Exemplo 1
Calcule A = (sen (2x - π) cos (3π - x) + sen (2x - 9π/2) cos (x + π/2)) 2 + (cos (x - π/2) cos ( 2x – 7π) /2) +
+
sen (3π/2 - x) sen (2x -5π/2)) 2
Solução.
Segue das fórmulas de redução:
sin (2x - π) \u003d -sen 2x; cos (3π - x) \u003d -cos x;
sin (2x - 9π / 2) \u003d -cos 2x; cos (x + π/2) = -sen x;
cos (x - π / 2) \u003d sin x; cos (2x - 7π/2) = -sen 2x;
sin (3π / 2 - x) \u003d -cos x; sin (2x - 5π / 2) \u003d -cos 2x.
De onde, em virtude das fórmulas para a adição de argumentos e a identidade trigonométrica básica, obtemos
A \u003d (sen 2x cos x + cos 2x sen x) 2 + (-sen x sen 2x + cos x cos 2x) 2 \u003d sen 2 (2x + x) + cos 2 (x + 2x) \u003d
= sen 2 3x + cos 2 3x = 1
Resposta 1.
Exemplo 2
Converta a expressão M = cos α + cos (α + β) cos γ + cos β – sen (α + β) sen γ + cos γ em um produto.
Solução.
Das fórmulas para a adição de argumentos e das fórmulas para converter a soma das funções trigonométricas em um produto, após o agrupamento apropriado, temos
М = (cos (α + β) cos γ - sen (α + β) sen γ) + cos α + (cos β + cos γ) =
2cos ((β + γ)/2) cos ((β – γ)/2) + (cos α + cos (α + β + γ)) =
2cos ((β + γ)/2) cos ((β – γ)/2) + 2cos (α + (β + γ)/2) cos ((β + γ)/2)) =
2cos ((β + γ)/2) (cos ((β – γ)/2) + cos (α + (β + γ)/2)) =
2cos ((β + γ)/2) 2cos ((β – γ)/2 + α + (β + γ)/2)/2) cos ((β – γ)/2) – (α + ( β + γ)/2)/2) =
4cos ((β + γ)/2) cos ((α + β)/2) cos ((α + γ)/2).
Resposta: М = 4cos ((α + β)/2) cos ((α + γ)/2) cos ((β + γ)/2).
Exemplo 3.
Mostre que a expressão A \u003d cos 2 (x + π / 6) - cos (x + π / 6) cos (x - π / 6) + cos 2 (x - π / 6) leva para todo x de R um e o mesmo valor. Encontre este valor.
Solução.
Apresentamos dois métodos para resolver este problema. Aplicando o primeiro método, isolando o quadrado completo e usando as correspondentes fórmulas trigonométricas básicas, obtemos
A \u003d (cos (x + π / 6) - cos (x - π / 6)) 2 + cos (x - π / 6) cos (x - π / 6) \u003d
4sen 2 x sen 2 π/6 + 1/2(cos 2x + cos π/3) =
Sin 2 x + 1/2 cos 2x + 1/4 = 1/2 (1 - cos 2x) + 1/2 cos 2x + 1/4 = 3/4.
Resolvendo o problema da segunda maneira, considere A como uma função de x de R e calcule sua derivada. Após as transformações, obtemos
А´ \u003d -2cos (x + π/6) sen (x + π/6) + (sen (x + π/6) cos (x - π/6) + cos (x + π/6) sen ( x + π/6)) - 2cos (x - π/6) sen (x - π/6) =
Sin 2(x + π/6) + sen ((x + π/6) + (x - π/6)) - sen 2(x - π/6) =
Sin 2x - (pecado (2x + π/3) + sen (2x - π/3)) =
sen 2x - 2sen 2x cos π/3 = sen 2x - sen 2x ≡ 0.
Assim, em virtude do critério de constância de uma função diferenciável em um intervalo, concluímos que
A(x) ≡ (0) = cos 2 π/6 - cos 2 π/6 + cos 2 π/6 = (√3/2) 2 = 3/4, x ∈ R. 
Resposta: A = 3/4 para x € R.
Os principais métodos para provar identidades trigonométricas são:
a) redução do lado esquerdo da identidade para o lado direito por transformações apropriadas;
b) redução do lado direito da identidade para a esquerda;
dentro) redução das partes direita e esquerda da identidade para a mesma forma;
G) redução a zero da diferença entre as partes esquerda e direita da identidade que está sendo provada.
Exemplo 4
Verifique se cos 3x = -4cos x cos (x + π/3) cos (x + 2π/3).
Solução.
Transformando o lado direito desta identidade de acordo com as fórmulas trigonométricas correspondentes, temos
4cos x cos (x + π/3) cos (x + 2π/3) =
2cos x (cos ((x + π/3) + (x + 2π/3)) + cos ((x + π/3) – (x + 2π/3))) =
2cos x (cos (2x + π) + cos π/3) =
2cos x cos 2x - cos x = (cos 3x + cos x) - cos x = cos 3x.
O lado direito da identidade é reduzido para o lado esquerdo.
Exemplo 5
Prove que sen 2 α + sen 2 β + sen 2 γ – 2cos α cos β cos γ = 2 se α, β, γ são ângulos internos de algum triângulo.
Solução.
Levando em conta que α, β, γ são ângulos internos de algum triângulo, obtemos que
α + β + γ = π e, portanto, γ = π – α – β.
sen 2 α + sen 2 β + sen 2 γ – 2cos α cos β cos γ =
Sin 2 α + sen 2 β + sen 2 (π - α - β) - 2cos α cos β cos (π - α - β) =
Sin 2 α + sen 2 β + sen 2 (α + β) + (cos (α + β) + cos (α - β) (cos (α + β) =
Sin 2 α + sen 2 β + (sen 2 (α + β) + cos 2 (α + β)) + cos (α - β) (cos (α + β) =
1/2 (1 - cos 2α) + ½ (1 - cos 2β) + 1 + 1/2 (cos 2α + cos 2β) = 2.
A igualdade original está provada.
Exemplo 6
Prove que para que um dos ângulos α, β, γ do triângulo seja igual a 60°, é necessário e suficiente que sen 3α + sen 3β + sen 3γ = 0.
Solução.
A condição deste problema pressupõe a prova tanto da necessidade quanto da suficiência.
Primeiro provamos precisar.
Pode ser mostrado que
sen 3α + sen 3β + sen 3γ = -4cos (3α/2) cos (3β/2) cos (3γ/2).
Assim, tendo em conta que cos (3/2 60°) = cos 90° = 0, obtemos que se um dos ângulos α, β ou γ for igual a 60°, então
cos (3α/2) cos (3β/2) cos (3γ/2) = 0 e, portanto, sen 3α + sen 3β + sen 3γ = 0.
Vamos provar agora adequação a condição especificada.
Se sen 3α + sen 3β + sen 3γ = 0, então cos (3α/2) cos (3β/2) cos (3γ/2) = 0 e, portanto,
ou cos (3α/2) = 0, ou cos (3β/2) = 0, ou cos (3γ/2) = 0.
Consequentemente,
ou 3α/2 = π/2 + πk, isto é. α = π/3 + 2πk/3, 
ou 3β/2 = π/2 + πk, i.e. β = π/3 + 2πk/3,
ou 3γ/2 = π/2 + πk,
Essa. γ = π/3 + 2πk/3, onde k ϵ Z.
Do fato de que α, β, γ são os ângulos de um triângulo, temos
0 < α < π, 0 < β < π, 0 < γ < π.
Portanto, para α = π/3 + 2πk/3 ou β = π/3 + 2πk/3 ou
γ = π/3 + 2πk/3 de todos os kϵZ apenas k = 0 se encaixa.
Daí segue que ou α = π/3 = 60°, ou β = π/3 = 60°, ou γ = π/3 = 60°.
A afirmação foi comprovada.
Você tem alguma pergunta? Não sabe como simplificar expressões trigonométricas?
Para obter a ajuda de um tutor - registre-se.
A primeira aula é grátis!
site, com cópia total ou parcial do material, é necessário um link para a fonte.



