Calcule um sistema de haste plano estaticamente indeterminado. Cálculo de sistemas estaticamente indeterminados pelo método de força

Os sistemas pivô são chamados de sistemas estaticamente indeterminados, nos quais apenas as equações de equilíbrio não são suficientes para determinar as reações dos apoios. Do ponto de vista cinemático, trata-se de sistemas de barras, cujo número de graus de liberdade é menor que o número de ligações. Para revelar a incerteza estática de tais sistemas, é necessário traçar equações adicionais para a compatibilidade das deformações. O número de tais equações é determinado pelo número de incerteza estática do sistema de haste. A Figura 8.14 mostra exemplos de vigas e pórticos estaticamente indeterminados.

O feixe mostrado na Figura 8.14b é chamado sem cortes feixe. Esse nome vem do fato de que o suporte intermediário suporta apenas a viga. No ponto de apoio, a viga não é cortada pela dobradiça, a dobradiça não é cortada no corpo da viga. Portanto, a influência das tensões e deformações que a viga experimenta no vão esquerdo também afeta o vão direito. Se, no local do suporte intermediário, a dobradiça for cortada no corpo da viga, então como resultado o sistema se tornará estaticamente determinado  de uma viga receberemos duas vigas independentes uma da outra, cada uma das quais será estaticamente determinado. Deve-se notar que as vigas contínuas são menos intensivas em materiais do que as vigas divididas, uma vez que distribuem os momentos fletores ao longo de seu comprimento de forma mais racional. Nesse sentido, as vigas contínuas são amplamente utilizadas na construção e na engenharia mecânica. No entanto, os feixes contínuos, por serem estaticamente indeterminados, requerem um método de cálculo especial que inclui o uso de deformações do sistema.

Antes de prosseguir com o cálculo de sistemas estaticamente indeterminados, é necessário aprender como determinar o grau de sua indeterminação estática. Uma das regras mais simples para determinar o grau de incerteza estática é a seguinte:

, (8.3)

Onde  o número de conexões impostas à estrutura;  o número de possíveis equações de equilíbrio independentes que podem ser elaboradas para o sistema em consideração.

Vamos usar a equação (8.3) para determinar o grau de incerteza estática dos sistemas mostrados na Figura 8.14.

A viga mostrada na Figura 8.14a é uma vez estaticamente indeterminada, uma vez que possui três elos no suporte esquerdo e um elo no suporte direito. Existem apenas três equações de equilíbrio independentes para tal viga. Assim, o grau de indeterminação estática do feixe
... A viga contínua mostrada na Figura 8.14b também é estaticamente indeterminada uma vez, uma vez que possui duas amarrações no suporte esquerdo e uma amarração cada no suporte intermediário e no suporte direito - apenas quatro amarrações. Assim, o grau de sua indefinibilidade estática
.

A moldura mostrada na fig. 8.14c, três vezes estaticamente indefinível, pois possui seis conexões nos suportes. Existem apenas três equações independentes de equilíbrio para este referencial. Assim, o grau de incerteza estática para este quadro da equação (8.3) é igual a:
... O grau de indeterminação estática da moldura mostrada na Figura 8.18, d é quatro, uma vez que a moldura possui sete elos nos suportes. Consequentemente, o grau de sua indeterminação estática é
.

A regra (8.3) para determinar o grau de incerteza estática aplica-se apenas a sistemas simples. Em casos mais complexos, essa regra não funciona. A Figura 8.15 mostra um quadro, o grau de incerteza estática da qual, usando a equação (8.3), não pode ser determinado.

Externamente, o sistema mostrado na Figura 8.15 é estaticamente indeterminado cinco vezes. Isso pode ser facilmente estabelecido usando a equação (8.3): três equações de equilíbrio possíveis são subtraídas de seis ligações externas (três na seção A, três na seção B e duas na seção C). No entanto, este sistema também possui indeterminação estática interna. É impossível levar em consideração a incerteza estática interna usando a equação (8.3). Antes de prosseguir com a definição do grau de incerteza estática do referencial mostrado na Figura 8.15, apresentamos várias definições. A primeira dessas definições inclui o conceito de dobradiça simples.

Simples chamada de dobradiça que conecta as duas hastes (Figura 8.16).

Figura 8.16. Dobradiça simples

Uma dobradiça conectando várias hastes é chamada complicado(Figura 8.17).

Figura 8.17. Dobradiça complexa

O número de dobradiças simples que podem substituir uma dobradiça complexa é determinado a partir da fórmula:

, (8.4)

Onde
 o número de hastes incluídas no nó.

Nós recalculamos a dobradiça complexa mostrada na Figura 8.17 para o número de dobradiças simples usando a fórmula (8.4):
... Assim, a dobradiça complexa mostrada na Figura 8.17 pode ser substituída por quatro dobradiças simples.

Vamos apresentar mais um conceito  circuito fechado.

Vamos provar o teorema: qualquer contorno fechado é estaticamente indefinido três vezes.

Para provar o teorema, considere um loop fechado carregado com forças externas (Figura 8.18).

Vamos cortar o contorno fechado com uma seção vertical e mostrar os fatores de força internos que surgem na seção. Em cada uma das seções, surgem três fatores internos: força de cisalhamento , momento de flexão
e força longitudinal
... No total, além das forças externas, seis fatores internos atuam em cada uma das partes de recorte do contorno (Figura 8.18, b, c). Considerando o equilíbrio de uma das partes de corte, por exemplo, a esquerda (Figura 8.18, b), descobrimos que o problema é estaticamente indefinível três vezes, já que para a parte de corte é possível compor apenas três equações de equilíbrio independentes, e as forças desconhecidas que atuam na parte de corte são seis ... Assim, o grau de indeterminação estática de um circuito fechado é
... O teorema está provado.

Agora, usando o conceito de uma dobradiça simples e um circuito fechado, podemos formular outra regra para determinar o grau de indeterminação estática:

, (8.5)

Onde
 número de contornos fechados;
 o número de dobradiças em termos de primos (8.4).

Usando a equação (8.5), determinamos o grau de incerteza estática do referencial mostrado na Figura 8.15. O quadro tem cinco contornos
, incluindo o contorno formado pelas barras de suporte. A dobradiça no nó D é simples porque conecta duas hastes. A dobradiça na seção K é complexa, pois conecta quatro hastes. O número de dobradiças simples que poderiam substituir a dobradiça na seção K é igual à fórmula (8.4):
... O pivô C também é complexo, pois conecta três hastes. Para esta dobradiça
... Além disso, o sistema possui mais duas dobradiças simples com as quais é preso à base. Assim, o número de dobradiças simples no sistema é
... Substituindo o número de loops fechados
e o número de juntas simples
na fórmula (8.5) determinamos o grau de incerteza estática da estrutura:
... Assim, mostrado na Fig. 8,15 quadro, sete vezes estaticamente indefinido. Isso significa que, para calcular tal sistema, é necessário compor, além das três equações de equilíbrio, sete equações de compatibilidade de deformações. Resolvendo o sistema de 10 equações assim obtido com respeito às incógnitas incluídas nessas equações, é possível determinar tanto as magnitudes das reações nas conexões externas quanto as forças internas que surgem no referencial. O procedimento para resolver este problema pode ser um tanto simplificado eliminando as equações de equilíbrio do sistema de equações. No entanto, essa abordagem requer o uso de métodos especiais de solução, um dos quais é o método das forças.

Os sistemas são chamados estaticamente indeterminados, cujas forças internas não podem ser determinadas apenas a partir das equações de equilíbrio (equações da estática).

Construções estaticamente indeterminadas têm os chamados supérfluo comunicação. Eles podem ocorrer em suportes, hastes e outros elementos. Tais conexões são chamadas de "supérfluas" porque não são necessárias para garantir o equilíbrio da estrutura, mas são condicionadas pelos requisitos de sua resistência e rigidez. Essas conexões extras são chamadas externo. Além disso, conexões desnecessárias podem surgir devido às peculiaridades do próprio design. Por exemplo, um contorno de quadro fechado (fig. 46, G) tem três forças internas desconhecidas em cada seção, ou seja, apenas seis, e três deles são "supérfluos". Esses esforços extras são chamados interno. Pelo número de conexões "extras" externas ou internas, estabeleça o grau de incerteza estática do sistema.É igual à diferença entre o número de incógnitas a serem determinadas e o número de equações estáticas. Com um desconhecido "extra", o sistema é chamado uma vez, ou uma vez estaticamente indefinível, com dois - duas vezes estaticamente indefinível e assim por diante.

A construção mostrada na fig. 46, uma, é uma vez estaticamente indeterminado e as construções mostradas na Fig. 46, b e v, - duas vezes estaticamente indeterminado, na Fig. 46, d - construção três vezes estaticamente indeterminada.

Na solução de problemas estaticamente indeterminados, além das equações estáticas, são utilizadas equações que levam em consideração as deformações dos elementos estruturais.

Existem vários métodos para resolver problemas estaticamente indeterminados: método de comparação de deslocamentos, método de forças, método de deslocamento.

Método de Força

Ao calcular sistemas estaticamente indeterminados, as forças são consideradas desconhecidas.

Cálculo por método de forças realizado na seguinte sequência:

• 1. Determine o grau de indeterminação estática.
• 2. Ao remover as conexões "extras", o sistema original é substituído por um estaticamente definível, chamado o sistema principal. Vários desses sistemas podem ser construídos, ao mesmo tempo que se observa a condição de seus

imutabilidade métrica.

• 3. O sistema principal é carregado com forças externas especificadas e forças desconhecidas "extras" que substituem a ação de conexões remotas, resultando em sistema equivalente.
• 4. Para garantir a equivalência dos sistemas inicial e básico, as forças desconhecidas devem ser selecionadas de modo que as deformações do sistema básico não sejam diferentes das deformações do sistema inicial estaticamente indeterminado. Para isso, o movimento dos pontos de aplicação das incógnitas "extras" na direção de sua ação é igualado a zero. A partir das equações adicionais obtidas desta forma, são determinados os valores dos esforços desconhecidos "extras". A determinação dos deslocamentos dos pontos correspondentes pode ser feita de qualquer maneira, mas é melhor usar o método de Mohr mais geral.
• 5. Após determinar os valores das forças desconhecidas "extras", as reações são determinadas e os diagramas das forças internas são traçados, as seções são selecionadas e a resistência é verificada da maneira usual.

Equações canônicas do método das forças

Equações adicionais de deslocamento, expressando a igualdade a zero dos deslocamentos nas direções das incógnitas "extras", convém compor nas chamadas Forma canônica, Essa. de acordo com um certo padrão. Vamos mostrar isso com o exemplo de solução do sistema estaticamente indeterminado mais simples (Fig. 47, uma).

Vamos escolher o console como sistema principal, descartando o suporte articulado. Obtemos um sistema equivalente após a aplicação de sua força externa T 7 e o "extra" desconhecido NS(fig. 47, b).

Equação canônica, que expressa a igualdade de deslocamento do ponto para zero V das forças F e NS, vai

Da equação nós temos

Para um sistema com duas restrições "extras", o sistema de equações canônicas tem a forma:

• 8 11 X 1 + b 12 ^ 2 + ^ 1
• 621- ^ 1 + 622 ^ 2 "I" ^ 20-

Movimentos A [p E b [y, incluídos nas equações canônicas, são determinados pelo método de Mohr.

Para sistemas que consistem em elementos retilíneos, é conveniente calcular os deslocamentos usando o método Vereshchagin.

Por exemplo, para o problema mostrado na Fig. 47, multiplicando os diagramas (Fig. 48), obtemos os coeficientes da equação canônica:

1 2 I 3 1 I / I 2 1 5 R1 3

E] b LL =-/ / -/ = -, E] A LR =-------- +-------.

1 11 2 3 3 1 1P 2 2 2 2 3 2/ 48 E]

Nós temos Chl - - = - E.

Tendo determinado a força NS, Na verdade, encontramos a reação de suporte Estou dentro. Além disso, o problema de determinar os fatores de força internos pode ser resolvido, como de costume, usando o método da seção.

MINISTÉRIO DA EDUCAÇÃO DA FEDERAÇÃO DA RÚSSIA

INSTITUIÇÃO ESTADUAL

UNIVERSIDADE TÉCNICA DO ESTADO DE KUZBASS

Departamento de Resistência de Materiais

CÁLCULO DE SISTEMAS DE HINGE-ROD ESTATICAMENTE NÃO DEFINIDOS DURANTE A TENSÃO - COMPRESSÃO

Instruções metódicas para a execução da tarefa computacional e gráfica sobre a resistência dos materiais para alunos de todas as especialidades

Compilado por V.D. Moiseenko

Aprovado em reunião de departamento Ata nº 8 de 29.06.01

Uma cópia eletrônica está na biblioteca do prédio principal da Instituição Estatal KuzGTU

Kemerovo 2002

Introdução. Escopo e propósito da atribuição

Um sistema de haste-dobradiça estaticamente indeterminado é aquele em que as forças nas hastes e as reações nos suportes não podem ser determinadas apenas a partir da condição de equilíbrio.

A Figura 1 mostra um suporte típico de duas barras. As forças N 1 e N 2 nas hastes deste suporte são facilmente determinadas a partir da condição de equilíbrio do sistema de forças convergentes aplicado ao nó de corte C, uma vez que duas equações para este sistema de forças com duas incógnitas são resolvidas.

Se a estrutura do suporte é complicada pela adição de mais uma barra (Fig. 1, b), então as forças nas barras não podem ser determinadas da mesma maneira, uma vez que para o nó C, apenas duas equações de equilíbrio estático ainda podem ser desenhadas up (ΣX = 0; ΣY = 0), e o número de esforços desconhecidos é três. Temos um sistema que já foi estaticamente indeterminado.

Complicando o projeto e introduzindo novas hastes, é possível obter um sistema estaticamente indeterminado duas vezes (ver Fig. 1, c), três vezes, etc. Consequentemente, por n vezes um sistema estaticamente indeterminado significa um sistema no qual o número de restrições excede o número de equações independentes da estática por n unidades.

Equações adicionais necessárias para resolver o problema podem ser encontradas considerando o sistema em um estado deformado e estabelecendo conexões entre os deslocamentos e as deformações dos elementos estruturais. As equações resultantes são chamadas de equações de compatibilidade de deformações.

A Figura 2 mostra diagramas de alguns sistemas estaticamente indeterminados.

Figura 2. Alguns tipos de sistemas estaticamente indeterminados

Ao estudar a seção "Sistemas de haste estaticamente indeterminados" e realizar esta tarefa gráfico-computacional, o aluno deve dominar os recursos de sistemas estaticamente indeterminados; adquirir habilidades na divulgação de indeterminação estática, na determinação de forças em elementos estruturais e na seleção de áreas transversais a partir da condição de resistência.

Na tarefa, o aluno precisa fazer o seguinte trabalho:

- determinar as forças nas hastes e selecionar as áreas transversais da ação de cargas externas;

- determinar tensões adicionais nas hastes de mudanças de temperatura;

- para determinar tensões de instalação adicionais causadas por imprecisões na fabricação de hastes;

- selecione as seções transversais das hastes de acordo com o estado limite.

O volume e a forma de execução da tarefa computacional e gráfica dependem do volume da unidade curricular estudada e são negociados pelo docente nas aulas práticas.

1. Breve informação teórica

Ao resolver problemas estaticamente indeterminados, a seguinte ordem deve ser seguida:

1.1. Considere o lado estático do problema. Construa um plano de forças e componha as equações da estática.

1.2. Considere o aspecto geométrico do problema. Elabore um plano de deslocamento. Elabore equações adicionais para a compatibilidade das deformações de tal forma que todas as forças desconhecidas possam ser encontradas.

1.3. Considere o lado físico do problema. De acordo com as leis da física (para cálculo de temperatura) e de acordo com a lei de Hooke, expressar deformações nas equações de sua compatibilidade por meio de forças desconhecidas que atuam nas hastes:

1.4. Realize uma solução conjunta das equações da estática, geometria, física e determine as forças desconhecidas.

1.5. Usando condições de resistência à compressão ou tração N / F = [σ], selecione as áreas da seção transversal das hastes.

1.6. Com as forças conhecidas nas barras e as áreas aceitas das seções transversais, calcule as tensões normais pela fórmula

σ = N F.

2. Exemplo

Dado: Uma viga AB absolutamente rígida é suportada, conforme mostrado na Fig. 3, carregada com uma carga uniformemente distribuída e uma força P.

Fig. 3. Diagrama de um sistema estaticamente indeterminado

Dados iniciais para cálculo

4. Determine as tensões totais nas hastes por ação de cargas, mudanças de temperatura e imprecisões de fabricação.

2.1. Cálculo de um sistema de haste articulada estaticamente indeterminado para carregamento externo

P = 30 kN q = 15 kN / m

A C B

Fig. 4. Esquema de projeto inicial

2.1.1. O lado estático do problema

O lado estático da tarefa é considerado pelo plano de força. Um plano de força é um diagrama de projeto que mostra todas as forças (conhecidas e desconhecidas) aplicadas a um elemento do sistema dobradiça-haste, cujo equilíbrio é considerado (em nosso caso, é uma viga rígida AB). Cortamos as hastes de aço e cobre e substituímos suas partes inferiores descartadas por forças internas (Fig. 5).

P = 30 kN q = 15 kN / m

A C B

60 °

Arroz. 5. Plano de forças de cargas externas

A partir do plano de forças (ver Fig. 5), escrevemos as equações de equilíbrio estático. Para responder à primeira pergunta do problema, é necessário conhecer as forças nas barras - aço e cobre. Neste caso, não há necessidade de calcular a reação do suporte fixo articulado. Portanto, dos três

possíveis equações estáticas (ΣX = 0; ΣY = 0; Σm c = 0) que escrevemos

aquele que não inclui as reações do suporte fixo articulado C:

∑ mC = 0

- N CT a + q a 2 2 + p a + NM sen 60o b = 0,

- N CT 2 + 15 2 2 2 + 30 2 - NM 0,866 4 = 0,

Após as ações algébricas, a equação de equilíbrio assume a forma

2.1.2. Lado geométrico do problema

O aspecto geométrico do problema é considerado pelo plano de movimento. Um plano de deslocamento é um diagrama de projeto que mostra a posição do sistema de haste da dobradiça antes e depois do carregamento. No plano de deslocamento, indicamos os deslocamentos dos pontos de viga (AA1 e BB1),

deformações absolutas de barras de cobre e aço (∆ l ST; ∆ l M)

(fig. 6). Além disso, devido às pequenas deformações, movemos os pontos do feixe verticalmente para cima ou para baixo e marcamos as deformações das hastes inclinadas com uma perpendicular.

Arroz. 6. Plano de deslocamento a partir da ação de cargas externas

De acordo com o plano de deslocamento, compomos a equação de compatibilidade de deformação. Em primeiro lugar, escrevemos a razão dos deslocamentos dos pontos de feixe a partir da semelhança dos triângulos AA1 C e SVB1 (Fig. 6):

Os deslocamentos dos pontos de feixe (AA1 e BB1) são expressos por meio de deformações

Substituímos as expressões (2.3) e (2.4) na relação (2.2):

2.1.3. O lado físico do problema

A equação de compatibilidade de deformação obtida (2.5) nesta forma não pode ser resolvida com a equação de equilíbrio (2.1), pois as incógnitas de natureza diferente nelas estão incluídas.

Deformações absolutas ∆ l CT e ∆ l M na equação (2.5) que expressamos

Recebida a equação de compatibilidade das deformações, escrita em termos das forças nas hastes.

2.1.4. Síntese

Vamos resolver juntos as equações de equilíbrio (2.1) e a equação de compatibilidade de deformação (2.6).

NCT + 1,73NM = 45

0,67NCT = 0,95NM.

A partir da segunda equação do sistema, expressamos o esforço N ST:

e substitua-o na primeira equação do sistema.

O resultado positivo de N ST e N M confirma nossas suposições de compressão da barra de aço e tensão da barra de cobre, o que significa que as forças nas barras serão:

2.1.5. Seleção de seções transversais de barras

A seleção das seções transversais das hastes é realizada de acordo com a condição de tração - resistência à compressão:

N F ≤ [σ].

a) A área da seção transversal da barra de aço exigida da condição de resistência será determinada:

b) A área da seção transversal da barra de cobre exigida pela condição de resistência será determinada:

Nesse caso, de acordo com uma determinada proporção de áreas, a área da barra de aço deve ser igual a:

FST = 4 3 FM = 4 3 1,7 10 - 4 = 1,275 10 - 4 m2 ..

Aceitamos grandes áreas de seção transversal de hastes:

Com as áreas transversais aceitas de barras de cobre e aço, determinamos as tensões nessas barras.

2 .2. Cálculo de temperatura de um sistema de haste de dobradiça estaticamente indeterminado

O objetivo do cálculo da temperatura é determinar as tensões adicionais nas barras de cobre e aço com as mudanças de temperatura.

Digamos que o sistema aqueça em ∆ t = 20 o C. O algoritmo da solução permanece o mesmo. O esquema de design inicial é mostrado na Fig. 7

Sistemas de bastão, reações de suporte e fatores de força internos nos quais não podem ser encontrados apenas nas equações de equilíbrio, são chamados estaticamente indefinido.

A diferença entre o número de forças desconhecidas buscadas e as equações de equilíbrio independentes determina grau de incerteza estática do sistema... O grau de indeterminação estática é sempre igual ao número de conexões redundantes (desnecessárias), cuja remoção transforma um sistema estaticamente indeterminado em um sistema estaticamente definível geometricamente imutável. Tanto as conexões externas (de suporte) quanto as internas, que impõem certas restrições ao movimento de seções do sistema entre si, podem ser redundantes.

Geometricamente imutável tal sistema é chamado, a mudança de forma do qual só é possível em conexão com as deformações de seus elementos.

Geometricamente variável tal sistema é denominado, cujos elementos podem mover-se sob a ação de forças externas sem deformação (mecanismo).

Mostrado na fig. 12.1 o quadro tem sete links externos (suporte). Para determinar os esforços nessas conexões (reações de suporte), apenas três equações de equilíbrio independentes podem ser traçadas. Portanto, este sistema possui quatro links redundantes, o que significa que é estaticamente indeterminado quatro vezes. Assim, o grau de incerteza estática para quadros planos é:

Onde R- o número de reações de apoio.

Um contorno constituído por uma série de elementos (retos ou curvos), rigidamente (sem dobradiças) interligados e formando uma corrente fechada, é denominado fechado . A moldura retangular mostrada na Figura 12.2 é um loop fechado. É estaticamente indefinível três vezes, pois para torná-lo estaticamente definível é necessário cortar um de seus elementos e eliminar três conexões extras. As reações dessas ligações são: força longitudinal, força transversal e momento fletor atuando no local do corte; eles não podem ser determinados usando as equações da estática. Em condições análogas, no sentido de indeterminação estática, existe qualquer circuito fechado, que é sempre três vezes estaticamente indefinido.

A inclusão de uma dobradiça no nó da estrutura, em que duas hastes convergem, ou colocá-la em qualquer lugar no eixo da haste remove uma conexão e reduz o grau geral de indeterminação estática em um. Essa dobradiça é chamada de única ou simples (Figura 12.3).

No caso geral, cada dobradiça incluída no nó de conexão c hastes, reduz o grau de incerteza estática em c-1 , uma vez que tal dobradiça substitui c-1 dobradiças simples (fig.12.3). Assim, o grau de incerteza estática do sistema na presença de malhas fechadas é determinado pela fórmula.

Um sistema estaticamente indeterminado é um sistema que não pode ser calculado usando apenas as equações da estática, uma vez que possui restrições desnecessárias. Para calcular tais sistemas, são elaboradas equações adicionais que levam em consideração as deformações do sistema.

Sistemas estaticamente indeterminados tem uma série de características:

1. Estaticamente indeterminado estruturas são mais rígidas do que as correspondentes estaticamente definível, uma vez que eles têm conexões adicionais.
2. em estaticamente indefinido sistemas, há menos esforços internos, o que determina sua eficiência em comparação com estaticamente definível sistemas com as mesmas cargas externas.
3. Quebrando conexões desnecessárias em estaticamente indefinido o sistema nem sempre leva à destruição, enquanto a perda de comunicação em estaticamente definível sistema o torna geometricamente variável.
4. Para cálculo estaticamente indefinido os sistemas devem ser predefinidos pelas características geométricas das seções transversais dos elementos, ou seja, de fato, por sua forma e tamanho, já que sua mudança leva a uma mudança de esforços nas conexões e a uma nova distribuição de esforços em todos os elementos do sistema.
5. Ao calcular estaticamente indefinido sistemas, é necessário selecionar o material de construção com antecedência, uma vez que é necessário conhecer seus módulos elásticos.
6. Em estaticamente indefinido sistemas, exposição à temperatura, assentamento de suportes, imprecisões na fabricação e instalação causam esforços adicionais.

O principal métodos de cálculoestaticamente indefinido os sistemas são:

1. Método de Força. Aqui, os esforços são considerados incógnitas - forças e momentos.
2.Método de deslocamento. Desconhecidos são fatores de deformação, como ângulos de giro e deslocamentos lineares.
3.Método misto. Aqui, algumas das incógnitas representam esforços e a outra parte - deslocamentos.
4... Método combinado.É usado no cálculo de sistemas simétricos para cargas desequilibradas. Acontece que é aconselhável calcular o sistema para a componente simétrica de uma dada carga pelo método do deslocamento, e para a componente inversamente simétrica - pelo método da força.
Além dos métodos analíticos indicados, vários métodos numéricos são usados ​​no cálculo de sistemas especialmente complexos.

Equações canônicas do método das forças

Para obter equações adicionais, que foram mencionadas na seção anterior, é necessário antes de tudo transformar o dado, n vezes estaticamente indefinido sistema, estaticamente definível, removendo conexões desnecessárias dele. O sistema estaticamente definível resultante é chamado básico. Observe que a transformação de um determinado sistema em um estaticamente definível é opcional. Às vezes, uma modificação do método de forças é usado, em que o sistema principal pode ser estaticamente indefinido entretanto, isso está além do escopo deste manual. A eliminação de quaisquer conexões não altera as forças internas e as deformações do sistema se forças e momentos adicionais forem aplicados a ele, que são as reações das conexões descartadas. Isso significa que se uma determinada carga e reações de conexões remotas forem aplicadas ao sistema principal, o sistema principal e os dados se tornarão equivalente.

Em um determinado sistema, não pode haver deslocamentos nas direções dos elos rígidos existentes, incluindo aqueles elos que foram descartados durante a transição para o sistema principal, portanto, no sistema principal, os movimentos nas direções dos elos descartados devem ser igual a zero. E, para isso, as reações das conexões descartadas devem ter significados estritamente definidos.

A condição de igualdade a zero do deslocamento na direção de qualquer i-ésima conexão de n rejeitada com base no princípio da independência da ação das forças tem a forma:

onde o primeiro índice denota a direção do movimento e o número do link descartado, e o segundo indica o motivo que causou o movimento, ou seja, - este é um movimento na direção da i-ésima ligação causado pela reação da k-ésima ligação; - deslocamento na direção da i-ésima ligação, causado pela ação simultânea de toda a carga externa.

No método das forças, a reação da k-ésima ligação é geralmente denotada por Xk. Levando em consideração esta designação e em virtude da validade da lei de Hooke, os deslocamentos podem ser representados na forma:

onde é um movimento único (ou específico) na direção da i-ésima ligação, causado pela reação, isto é, uma reação que coincide na direção com Xk, mas igual a um.

Substituindo (2) por (1), obtemos:

Sentido físico equações (3): o deslocamento no sistema principal na direção da i-ésima conexão descartada é igual a zero.

Escrevendo expressões semelhantes a (3) para todo o conjunto de conexões descartadas, obtemos sistema de equações canônicasmétodo de forças:

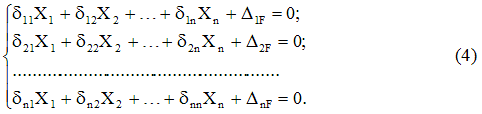
A forma da equação (4), ou seja, o número de termos em cada um deles e seu número total é determinado apenas pelo grau de incerteza estática do sistema e não depende de suas características específicas.

Os coeficientes do sistema de equações canônicas (4) são determinados pelo método de Mohr-Vereshchagin pela multiplicação dos diagramas correspondentes. Todos esses fatores, conforme indicado acima, representam deslocamentos; os coeficientes para as incógnitas são deslocamentos de unidades, e os termos livres são frete. Os movimentos individuais são divididos em a Principal, localizado na diagonal principal e tendo os mesmos índices e garantia(). Os principais deslocamentos são sempre positivos, ao contrário dos laterais. Os deslocamentos localizados simetricamente de acordo com o teorema da reciprocidade dos deslocamentos são iguais entre si, ou seja, ...

Algoritmo para cálculo pelo método das forças

Independentemente das características do projeto em consideração, a seguinte sequência de cálculo de sistemas estaticamente indeterminados pode ser distinguida método de força:

1. Determine grau de incerteza estática.
2. Selecione o sistema principal.
3. Forme um sistema equivalente.
4. Registre o sistema equações canônicas.
5. Construir diagramas simples e de carga dos fatores de força interna que surgem nos elementos da estrutura em consideração.
6. Calcule os coeficientes das incógnitas e os termos livres do sistema de equações canônicas.
7. Construa um gráfico de unidade de resumo.
8. Execute uma verificação universal de coeficientes para membros desconhecidos e livres.
9. Resolva o sistema (4), ou seja, determinar as reações de conexões desnecessárias.
10. Construa diagramas dos fatores de força internos decorrentes para um determinado sistema (em outras palavras, diagramas finais).
11. Realize verificações estáticas e cinemáticas.
Observe que os pontos 7, 8, 11 do algoritmo acima não são absolutamente necessários, embora permitam que você controle a exatidão do cálculo. E para sistemas com uma conexão extra, os pontos 7 e 8 simplesmente não têm sentido, pois neste caso o diagrama da unidade total coincide com a unidade um.
Detenhamo-nos em mais detalhes em alguns dos estágios de cálculo acima.

Selecionando o sistema principal

Esta é a etapa mais importante do cálculo, uma vez que a escolha racional do sistema principal simplifica muito o trabalho computacional. Considere as possíveis maneiras de remover links desnecessários, o que determina o tipo do sistema principal.

1. O descarte de dormentes desnecessários efetua-se removendo completamente alguns dos suportes ou substituindo-os por suportes com menos dormentes. As reações que atuam na direção das conexões descartadas são incógnitas desnecessárias. A Figura 1, b, c, d mostra várias variantes do sistema equivalente obtido por este método para o quadro (Figura 1, a).

2. A colocação das dobradiças nas secções intermédias das hastes permite em cada uma dessas secções estabelecer uma ligação correspondente ao momento flector. Esses momentos são incógnitas supérfluas. Para um pórtico com grau de incerteza estática n = 3 (Fig. 2, a), na escolha do sistema principal é necessário colocar três dobradiças. A posição dessas dobradiças pode ser arbitrária, mas satisfazendo o requisito de imutabilidade geométrica do sistema (Fig. 2, b).

3. A dissecção da barra elimina três ligações correspondentes às forças internas M, Q, N (Fig. 2, c). Em casos especiais (Fig. 2, d), a dissecção da haste ao longo da dobradiça libera duas ligações (Fig. 2, e), e a dissecção de uma haste retilínea com dobradiças nas extremidades - uma ligação (Fig. 2, f).

Entre os links de um sistema estaticamente indefinível, existem os absolutamente necessários e os condicionalmente necessários. Absolutamente necessários são os links, quando removidos, o sistema torna-se geometricamente variável. Uma conexão absolutamente necessária é caracterizada pela determinabilidade estática do esforço nela, ou seja, a reação de tal ligação pode ser calculada a partir da condição de equilíbrio. Ao escolher um sistema básico, as conexões absolutamente necessárias não podem ser descartadas.

As conexões, quando removidas, o sistema continua a permanecer geometricamente inalterado, são chamadas de condicionalmente necessárias. O sistema para o qual esse link foi removido pode ser o sistema principal. método de forças.

Cálculo de coeficientes e termos livres de equações canônicas

Esta etapa do cálculo é precedida da construção de diagramas unitários e de carga dos fatores de força internos (para vigas e pórticos - diagramas de momentos fletores). Os diagramas de unidade são construídos a partir da ação de uma força unitária adimensional ou de um momento unitário adimensional, coincidindo na direção com a direção da incógnita supérflua correspondente no sistema equivalente, e são denotados por, e um diagrama de unidade por meio.

O diagrama de carga é construído a partir de uma carga externa aplicada ao sistema principal. Neste caso, você pode construir um diagrama a partir da ação simultânea de todas as cargas externas ou vários diagramas, separadamente de cada uma das cargas aplicadas. Tal divisão de um diagrama de carga em vários outros mais simples, via de regra, é aconselhável apenas quando entre as cargas atuantes há uma uniformemente distribuída e o diagrama de momentos na seção correspondente abaixo dela é alternado. Além disso, em cada equação canônica, o número de termos livres será igual ao número de diagramas de carga construídos.

Os deslocamentos de unidades e cargas (coeficientes e termos livres das equações canônicas) no caso geral podem ser calculados pelo método de Mohr. Para vigas e quadros, isso pode ser feito usando a regra de Vereshchagin.

Verificação universal de coeficientes e termos livres de equações canônicas

Para realizar uma verificação universal, é necessário construir um diagrama de unidade total - um diagrama de momentos da ação simultânea de todas as forças de unidade aplicadas ao sistema principal:

Vamos multiplicar o gráfico da unidade total pelo gráfico:

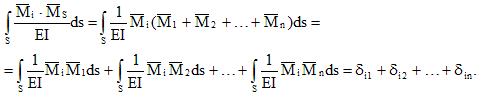
Assim, o resultado da multiplicação do total e dos diagramas de unidade i-ésima é um movimento na direção da i-ésima conexão da ação conjunta de desconhecidos extras únicos. Este deslocamento é igual à soma dos coeficientes da i-ésima equação canônica:

Esta verificação é chamada linha por linha e é satisfeito para cada equação canônica.
Em vez de n verificações linha por linha, uma é mais frequentemente realizada - verificação universal, que consiste em multiplicar o diagrama da unidade total por si mesmo e verificar a condição:

Se a verificação universal for realizada, os movimentos da unidade são calculados corretamente; caso contrário, é necessário realizar verificações linha a linha, que permitirão esclarecer o movimento em cujo cálculo foi cometido um erro.

Para verificar os movimentos de carga, é necessário multiplicar a unidade total e os diagramas de carga dos momentos fletores:

Assim, verificar os termos livres do sistema de equações canônicas (4) consiste em cumprir a condição.