三角方程式の簡略化。 三角関数の恒等変換
ビデオ レッスン「三角関数の式の簡略化」は、基本的な三角関数の恒等式を使用して三角関数の問題を解くスキルを向上させるように設計されています。 ビデオレッスンでは、三角関数の恒等式の種類と、それらを使用した問題解決の例について検討します。 視覚補助を使用すると、教師はレッスンの目的を達成しやすくなります。 教材の鮮やかなプレゼンテーションは、重要なポイントの記憶に役立ちます。 アニメーション効果や声優を使うことで、教材を説明する段階で教師を完全に置き換えることができます。 したがって、教師は数学の授業でこの視覚補助を使用すると、指導の効果を高めることができます。
ビデオレッスンの最初に、そのトピックが発表されます。 次に、以前に検討した三角関数の恒等式が思い出されます。 画面には等式 sin 2 t+cos 2 t=1、tg t=sin t/cos t、kϵZ の場合は t≠π/2+πk、ctg t=cos t/sin t、t≠πk の場合は true、が表示されます。ここで kϵZ、tg t · ctg t=1、t≠πk/2 で、kϵZ、基本三角恒等式と呼ばれます。 これらの恒等式は、等価性を証明したり式を簡素化する必要がある問題を解決する際によく使用されることに注意してください。
さらに、問題解決におけるこれらのアイデンティティの適用例も考慮されます。 まず、表現を簡略化する問題の解決を検討することを提案します。 例 1 では、式 cos 2 t- cos 4 t+ sin 4 t を簡略化する必要があります。 この例を解決するには、まず共通因数 cos 2 t を括弧で囲みます。 括弧内のこのような変換の結果、式 1-cos 2 t が得られます。三角法の基本恒等式からその値は sin 2 t に等しくなります。 式の変換後、もう 1 つの共通因数 sin 2 t を括弧から取り出すことができることは明らかで、その後、式は sin 2 t (sin 2 t + cos 2 t) の形式になります。 同じ基本的な同一性から、括弧内の式の値は 1 に等しいと推定されます。単純化の結果、cos 2 t-cos 4 t+ sin 4 t= sin 2 t が得られます。
例 2 では、コスト/(1- sint)+ コスト/(1+ sint) という式も簡略化する必要があります。 式コストは両方の分数の分子に含まれるため、共通因数として括弧に入れることができます。 次に、括弧内の分数は、(1- sint)(1+ sint) を乗算して共通の分母に減算されます。 類似の項を削減すると、分子には 2 が残り、分母には 1 - sin 2 t が残ります。 画面の右側では、基本的な三角関数の単位 sin 2 t+cos 2 t=1 が表示されます。 これを使用して、分数 cos 2 t の分母を求めます。 端数を減らすと、コスト/(1- sint)+コスト/(1+sint)=2/コストという式の簡略化された形式が得られます。
次に、三角法の基本恒等法について得た知識を応用した恒等証明の例を考えます。 例3では、同一性(tg 2 t-sin 2 t)・ctg 2 t=sin 2 tを証明する必要がある。 画面の右側には、証明に必要な 3 つの恒等式、tg t ctg t=1、ctg t=cos t/sin t、制限付き tg t=sin t/cost が表示されます。 同一性を証明するには、最初に括弧が開かれ、その後、主要な三角関数の恒等式 tg t・ctg t=1 の式を反映する積が形成されます。 次に、コタンジェントの定義からの恒等式に従って、ctg 2 t が変換されます。 変換の結果、式 1-cos 2 t が得られます。 基本的なアイデンティティを使用して、式の値を見つけます。 したがって、(tg2t−sin2t)・ctg2t=sin2tであることが証明される。

例 4 では、tg t+ctg t=6 の場合、式 tg 2 t+ctg 2 t の値を見つける必要があります。 式を評価するには、まず方程式 (tg t+ctg t) 2 =6 2 の右辺と左辺を 2 乗します。 省略された乗算式が画面の右側に表示されます。 式の左側の大括弧を開くと、合計 tg 2 t+2 tg t ctg t+ctg 2 t が形成されます。その変換には、三角恒等式 tg t ctg t=1 のいずれかを適用できます。そのフォームは画面の右側に表示されます。 変換後、等式tg 2 t+ctg 2 t=34が得られる。 等式の左辺は問題の条件と一致するので、答えは 34 になります。問題は解決されました。
ビデオレッスン「三角関数の式の簡略化」は、伝統的な学校の数学の授業での使用をお勧めします。 また、この教材は遠隔教育を提供する教師にも役立ちます。 三角関数の問題を解くスキルを身につけるため。
テキストの解釈:
「三角関数の式の簡略化」。
平等
1)sin 2 t + cos 2 t = 1 (サイン 2 乗 te とコサイン 2 乗 te は 1 に等しい)
2) tgt =、t ≠ + πk、kϵZ (te が pi に 2 を加えたものに pi ka を加えたものではない場合、te の正接は te のサインと te のコサインの比に等しく、ka は zet に属します)
3) ctgt = 、t ≠ πk、kϵZ で (te が z に属する ka のピークと等しくない場合、te の余弦は te の余弦と te の正弦の比に等しくなります)。
4) tgt ∙ ctgt = 1 (t ≠ , kϵZ の場合)
は基本三角恒等式と呼ばれます。
多くの場合、三角関数の式を簡略化して証明する際に使用されます。
三角関数の式を簡略化するときにこれらの公式を使用する例を考えてみましょう。
例 1. 式を簡略化します: cos 2 t - cos 4 t + sin 4 t。 (式 a コサイン 2 乗 te マイナス te の 4 次のコサイン + te の 4 次のサイン)。
解決。 cos 2 t - cos 4 t + sin 4 t = cos 2 t∙ (1 - cos 2 t) + sin 4 t = cos 2 t ∙ sin 2 t + sin 4 t = sin 2 t (cos 2 t + sin 2) t) = sin 2 t 1= sin 2 t
(共通因数のコサイン 2 乗 te を取り出します。括弧内で 1 とコサイン te の 2 乗の差を求めます。これは、最初の恒等式によるサイン te の 2 乗に等しいです。4 番目のサインの合計を取得します。コサイン二乗 te とサイン二乗 te の積の次数 te。括弧の外側の共通因数サイン二乗 te を取り出し、括弧内でコサインとサインの二乗の和を取得します。これは、基本的な三角関数に従って、恒等式は 1 に等しい。その結果、正弦 te) の 2 乗が得られます。
例 2. 式を単純化します: + 。
(式 be は、分母 1 から正弦 TE を引いた最初の余弦 TE の分子と、分母に 2 番目の余弦 TE に正弦 TE を加えた 2 番目の余弦 TE の分子の 2 つの分数の合計です。)
(共通因数の余弦 te を括弧から取り出し、括弧内でそれを公分母に導きます。これは、1 マイナスサイン TE と 1 プラスサイン TE の積です。
分子では、1 プラスサイン テ プラス 1 マイナスサイン テを取得します。同様のものを与えます。同様のものを取得すると、分子は 2 に等しくなります。
分母では、省略された乗算公式 (二乗の差) を適用して、単位と正弦関数の二乗の差を取得できます。これは、基本的な三角関数の恒等式に従って、
はコサイン te の 2 乗に等しい。 コサイン te で減算すると、最終的な答え (2 をコサイン te で割ったもの) が得られます。
三角関数の式の証明におけるこれらの公式の使用例を考えてみましょう。
例 3. 同一性を証明する (tg 2 t - sin 2 t) ∙ ctg 2 t \u003d sin 2 t (te の正接と te の正弦の二乗の差と、余接の二乗の積) te は te の正弦の 2 乗に等しい)。
証拠。
等式の左辺を変形してみましょう。
(tg 2 t - sin 2 t) ∙ ctg 2 t = tg 2 t ∙ ctg 2 t - sin 2 t ∙ ctg 2 t = 1 - sin 2 t ∙ ctg 2 t =1 - sin 2 t ∙ = 1 - cos 2 t = 罪 2 t
(括弧を開けましょう。以前に得られた関係から、te の正接の 2 乗と te の余接との積は 1 に等しいことがわかっています。te の余接は、次の余弦の比に等しいことを思い出してください。 te と te のサイン。これは、コタンジェントの 2 乗が te のサインの 2 乗に対する te のコサインの 2 乗の比であることを意味します。
te の正弦二乗による削減後、1 と te の二乗の余弦との差が得られます。これは、te の二乗の正弦に等しいです)。 Q.E.D.

例 4. tgt + ctgt = 6 の場合、式 tg 2 t + ctg 2 t の値を求めます。
(正接と余接の合計が 6 の場合、te の正接と余接の 2 乗の合計)。
解決。 (tgt + ctgt) 2 = 6 2
tg 2 t + 2 ∙ tgt ∙ ctgt + ctg 2 t = 36
tg 2 t + 2 + ctg 2 t = 36
tg 2 t + ctg 2 t = 36-2
tg 2 t + ctg 2 t = 34
元の等式の両方の部分を二乗してみましょう。
(tgt + ctgt) 2 = 6 2 (te の正接と te の余接の和の 2 乗は 6 の 2 乗です)。 省略された乗算の公式を思い出してください。2 つの量の合計の 2 乗は、最初の量の 2 乗に、1 番目と 2 番目の積の 2 倍を加えた 2 番目の量の 2 乗を加えたものに等しくなります。 (a+b) 2 =a 2 +2ab+b 2 tg 2 t + 2 ∙ tgt ∙ctgt + ctg 2 t = 36 が得られます。

teのタンジェントとteのコタンジェントの積は1に等しいため、tg 2 t + 2 + ctg 2 t \u003d 36(teのタンジェントとteと2のコタンジェントの二乗の合計は次のようになります) 36)、
ヴォロンコワ オルガ・イワノヴナ
MBOU「中等学校」
No.18」
エンゲルス、サラトフ地方。
数学の先生。
「三角関数の式とその変換」
はじめに……………………………………………………………………………………3
第 1 章 三角関数の変換を使用するタスクの分類 ……………………………………………………………………5
1.1. 計算タスク 三角関数の値………….5
1.2.三角関数式を簡略化するためのタスク ..... 7
1.3. 三角関数の数値式を変換するためのタスク ... ..7
1.4 混合タスク………………………………………………………………9
第2章
2.1 10 年生におけるテーマの繰り返し……………………………………………………11
テスト 1……………………………………………………………………..12
テスト 2…………………………………………………………………………..13
テスト 3…………………………………………………………………………..14
2.2 11 年生の最終留年…………………………………………………………15
テスト 1…………………………………………………………………………..17
テスト 2…………………………………………………………………………..17
テスト 3…………………………………………………………………………..18
結論……………………………………………………………………………………19
使用文献リスト………………………………………………..20
導入。
今日の状況において最も重要な問題は、「生徒の知識のギャップをどのように解消し、試験で起こり得る間違いを警告するにはどうすればよいでしょうか?」ということです。 この問題を解決するには、生徒がプログラム教材を正式に理解するのではなく、その深く意識的な理解、口頭計算と変換の速度の向上、そして最も単純な問題を解決するためのスキルの開発を達成する必要があります。 「心の中にある」問題。 数学の学習において、実践的なスキルの習得とその使用を条件として、積極的な立場にある場合にのみ、真の成功を期待できることを生徒に納得させる必要があります。 10 年生から 11 年生の選択科目を含む、あらゆる機会を利用して試験の準備をし、生徒と一緒に複雑な課題を定期的に分析し、教室や追加授業でそれらを解決する最も合理的な方法を選択する必要があります。肯定的な結果が得られる典型的な問題を解決する領域は、数学教師であれば、作成することで達成できます。生徒の優れた基礎訓練、私たちの前に開かれた問題を解決するための新しい方法を探すこと、積極的に実験すること、生徒の効果的な自己実現と自己決定のための好ましい条件を生み出す現代の教育技術、方法、技術を適用すること。新しい社会情勢。
三角法は学校の数学コースに不可欠な部分です。 三角法の優れた知識と強力なスキルは、十分なレベルの数学的教養の証拠であり、数学、物理学、および多くの専門知識の研究を成功させるために不可欠な条件です。規律。
作品の関連性. 合格率の分析以来、過去数年の結果(2011 年の修了率は 48.41%、2012 年の修了率は 51.05%)で明らかなように、学校卒業生のかなりの部分は、数学のこの重要なセクションでの準備が年々非常に不十分であることを示しています。州の統一試験では、学生がこの特定のセクションの課題を完了する際に多くの間違いを犯しているか、そのような課題にまったく取り組んでいないことが判明しました。 ひとつに 三角法の州試験問題は、ほぼ 3 種類のタスクで出題されます。 これは、タスク B5 の最も単純な三角方程式の解法であり、タスク B7 の三角関数の式の使用、タスク B14 およびタスク B12 の三角関数の学習です。タスク B12 では、物理現象を記述し、三角関数を含む公式が存在します。 。 これはタスク B の一部にすぎません。 しかし、根を選択するお気に入りの三角方程式 C1 や、「あまり好きではない」幾何学的タスク C2 と C4 もあります。
仕事の目標. 三角関数の式の変換に特化した USE タスク B7 の内容を分析し、テストでのプレゼンテーションの形式に従ってタスクを分類します。
作品は序章と結論の2章から構成されています。 導入部では作品の関連性を強調しています。 最初の章では、統一国家試験 (2012 年) のテスト課題で三角関数の式の変換を使用するための課題の分類を示します。
第 2 章では、10 年生と 11 年生の「三角関数の式の変換」というトピックの繰り返しの構成が検討され、このトピックに関するテストが開発されます。
参考文献のリストには 17 件の情報源が含まれています。
第 1 章 三角関数の変換を使用するためのタスクの分類。
中等(完全)教育の基準と学生の訓練レベルの要件に従って、三角法の基礎の知識に関する課題が要件の体系化に含まれています。
三角法の基礎を学ぶことは、次の場合に最も効果的です。
生徒は以前に学習した内容を繰り返すよう積極的に動機づけられます。
教育過程では学生中心のアプローチが導入されます。
学生の知識の拡大、深化、体系化に貢献するタスクのシステムが適用されます。
高度な教育技術が使用されます。
試験の準備のために文献とインターネット リソースを分析した後、私たちはタスク B7 (KIM USE 2012-三角法) の可能な分類の 1 つを提案しました。三角関数の式の値。 の割り当て三角関数の数値式の変換。 リテラル三角関数式の変換のための代入。 混合タスク。
1.1. 計算タスク 三角関数の式の値。
最も一般的なタイプの単純な三角関数の問題の 1 つは、三角関数の値をそれらの 1 つの値によって計算することです。
a) 基本的な三角関数の恒等式とその帰結の使用。
例1
。 どうかを見つける  そして
そして  .
.
解決。  ,
,  ,
,
なぜなら 、 それ  .
.
答え。
例 2
。 探す  、 もし
、 もし  そして 。
そして 。
解決。  ,
,  ,
,  .
.
なぜなら 、 それ  .
.
答え。 。
b) 倍角公式の使用。
例 3
。 探す  、 もし
、 もし  .
.
解決。 、  .
.
答え。  .
.
例 4
。 式の値を見つける  .
.
解決。 。
答え。  .
.
1. 探す 、 もし
 そして
そして  。 答え。 -0.2
。 答え。 -0.2 2.
探す 、 もし  そして
そして  。 答え。 0.4
。 答え。 0.4
 、 もし 。 答え。 -12.884.
探す
、 もし 。 答え。 -12.884.
探す  、 もし
、 もし  。 答え。 -0.845.
式の値を見つけます。
。 答え。 -0.845.
式の値を見つけます。 。 答え。 66.
式の値を見つける
。 答え。 66.
式の値を見つける .答え。 -19
.答え。 -191.2.三角関数の式を簡略化するためのタスク。 リダクション公式は、幾何学、物理学、およびその他の関連分野の授業でさらに使用されるため、学生はよく習得する必要があります。
例5
.
式を簡略化する  .
.
解決。 。
答え。  .
.
独立したソリューションのタスク:
1. 式を簡略化する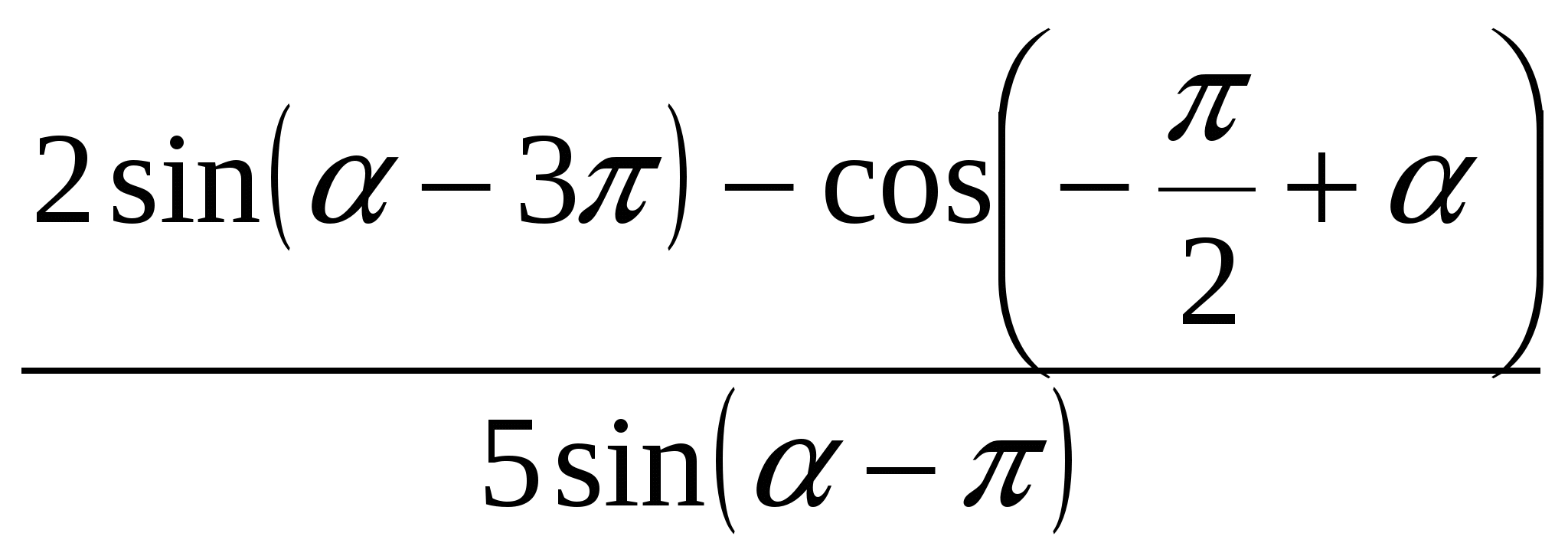 .
答え。 0.62.
探す
.
答え。 0.62.
探す  、 もし
、 もし  そして。 答え。 10.563.
式の値を見つける
そして。 答え。 10.563.
式の値を見つける  、 もし
、 もし  .
答え。 2
.
答え。 2 1.3. 三角関数の数値式を変換するタスク。
三角関数の数値式を変換するタスクのスキルと能力を開発するときは、三角関数の値の表、三角関数のパリティと周期性の特性に関する知識に注意を払う必要があります。
a) いくつかの角度に対して三角関数の正確な値を使用します。
例6
。 計算する  .
.
解決。  .
.
答え。  .
.
b) パリティの特性を使用する 三角関数。
例 7
。 計算する  .
.
解決。 .
答え。 
V) 周期性プロパティの使用三角関数。
例8
.
式の値を見つける  .
.
解決。 。
答え。  .
.
独立したソリューションのタスク:
1. 式の値を見つける .
答え。 -40.52. 式の値を見つける
.
答え。 -40.52. 式の値を見つける  .
答え。 17
.
答え。 17 3.
式の値を見つける  .
答え。 6
.
答え。 6
 .
答え。 -24
.
答え。 -24  答え。 -64
答え。 -641.4 混合タスク。
認定のテスト形式には非常に重要な特徴があるため、複数の三角関数の公式を同時に使用することに関連するタスクに注意を払うことが重要です。
例9
探す  、 もし
、 もし  .
.
解決。  .
.
答え。  .
.
例 10
。 探す  、 もし
、 もし  そして
そして  .
.
解決。 .
なぜなら 、 それ  .
.
答え。  .
.
例11.
探す  、 もし 。
、 もし 。
解決。 , ,  ,
,  ,
,  ,
,  ,
,  .
.
答え。
例12。
計算する  .
.
解決。 .
答え。  .
.
例 13
式の値を見つける  、 もし
、 もし  .
.
解決。 .
答え。  .
.
独立したソリューションのタスク:
1. 探す 、 もし
、 もし  .
答え。 -1.75
.
答え。 -1.752. 探す
 、 もし
、 もし  .
答え。 33. 探す
.
答え。 33. 探す  、 もし 。答え。 0.254. 式の値を見つける
、 もし 。答え。 0.254. 式の値を見つける  、 もし
、 もし  .
答え。 0.35. 式の値を見つける
.
答え。 0.35. 式の値を見つける  、 もし
、 もし  .
答え。 5
.
答え。 5第 2 章。トピック「三角関数の式の変換」の最後の繰り返しの方法論的側面の整理。
学力のさらなる向上に貢献する最も重要な課題の 1 つは、学生が深く確かな知識を獲得することです。これは、以前に学習した内容を反復するという問題です。 実践してみると、10年生ではテーマの繰り返しを組織する方がより便利であることがわかります。 11年生 - 最後の繰り返し。
2.1. 10年生のテーマの繰り返し。
数学的教材に取り組む過程では、完了した各トピックまたはコースのセクション全体を繰り返すことが特に重要になります。
テーマの繰り返しにより、そのテーマに関する生徒の知識は、その通過の最終段階または休憩後に体系化されます。
テーマの繰り返しの場合は、特別なレッスンが割り当てられ、特定のトピックの内容が集中して一般化されます。
レッスンの繰り返しは会話を通じて行われ、この会話には生徒が幅広く参加します。 その後、学生には特定のトピックを繰り返す課題が与えられ、テストで単位取得が必要になることが警告されます。
トピックに関するテストには、その主要な質問がすべて含まれている必要があります。 作業が完了したら、特徴的なエラーが分析され、それらを排除するために繰り返しが組織されます。
テーマの繰り返しのレッスンのために、私たちは開発されたものを提供します 試験用紙トピック「三角関数の式の変換」について。
テスト #1
テスト #2
テスト #3
解答表
テスト
2.2. 11年生の最後の繰り返し。
最後の繰り返しは、数学コースの主要な問題を学習する最終段階で実行され、このセクションまたはコース全体の教材の学習と論理的に関連して実行されます。
教材の最後の繰り返しには次の目標があります。
1. トレーニングコース全体の内容を活性化して、その論理構造を明確にし、主題および主題間の関係内でシステムを構築します。
2. 繰り返しの過程で、コースの主要な問題に関する学生の知識を深め、可能であれば拡大します。
すべての卒業生に数学の必須試験が課せられる中、USE の段階的な導入により、教師はすべての生徒が基礎レベルで教材を確実に習得する必要性を考慮して、授業の準備と実施に新しいアプローチを採用することになります。大学入学に向けて高得点を獲得することに関心のある意欲的な学生にとっては、より高いレベルでの学習内容の習得におけるダイナミックな進歩の機会となります。
最後の繰り返しのレッスンでは、次のタスクを検討できます。
例1 . 式の値を計算します。解決。 = = =
= =  =
= =
= =
= =0,5.
答え。 0.5。 例 2
式が取り得る最大の整数値を指定します
=0,5.
答え。 0.5。 例 2
式が取り得る最大の整数値を指定します  .
.
解決。 なぜなら  セグメント [-1; に属する任意の値を取ることができます。 1]、その後
セグメント [-1; に属する任意の値を取ることができます。 1]、その後  セグメント [-0.4; 0.4】なので。 式の整数値は 1、つまり数値 4 です。
セグメント [-0.4; 0.4】なので。 式の整数値は 1、つまり数値 4 です。
 .
.
解決策: 立方体の和を因数分解する公式を使用しましょう。 我々は持っています
我々は持っています:  .
.
答え: 1
例 4
計算する  .
.
解決。 。
答え: 0.28
最後の繰り返しのレッスンでは、「三角関数の式の変換」というトピックに関する開発されたテストを提供します。
1を超えない最大の整数を指定してください
結論.
このトピックに関する関連する方法論の文献を調べた結果、学校の数学コースで三角関数変換に関連するタスクを解決する能力とスキルが非常に重要であると結論付けることができます。
行われた作業の過程で、タスクB7の分類が実行されました。 2012 年の CMM で最も頻繁に使用された三角関数の公式を検討します。 タスクの例と解決策が示されています。 微分可能なテストは、試験の準備において知識の反復と体系化を組織化するために開発されました。
を考慮して、開始した作業を続行することをお勧めします。 タスク B5 では最も単純な三角方程式の解法、タスク B14 では三角関数の学習、タスク B12 では、物理現象を記述し、三角関数を含む公式が存在します。
結論として、試験に合格する効果は、あらゆる教育レベル、あらゆるカテゴリーの生徒に対して準備プロセスがどれだけ効果的に組織されるかによって主に決まるということを指摘しておきたいと思います。 そして、生徒の自主性、責任感、その後の人生を通して学び続ける姿勢を形成することができれば、国家や社会の秩序を満たすだけでなく、私たち自身の自尊心も高めることができます。
教材を繰り返すには、教師の創造的な作業が必要です。 反復の種類間の明確な関係を提供し、深く考え抜かれた反復システムを実装する必要があります。 繰り返しを組織化する技術を習得するのは教師の仕事です。 学生の知識の強さは、その解決策に大きく依存します。
文学。
Vygodsky Ya.Ya.、初等数学のハンドブック。 -M.: ナウカ、1970 年。
代数の難易度が上がる課題と解析の始まり: 高校 10 ~ 11 年生用の教科書 / B.M. イヴレフ、A.M. アブラモフ、Yu.P. ドゥドニツィン、S.I. シュヴァルツブルド。 – M.: 啓蒙、1990 年。
基本的な三角関数の式の変換への応用 (10 年生) // 教育的アイデアの祭典。 2012年から2013年。
コリャノフ A.G. 、プロコフィエフ A.A. 私たちは優秀な学生と優秀な学生を試験に向けて準備します。 - M.: 教育大学「9 月 1 日」、2012 年。- 103 p。
クズネツォワ E.N.三角関数式の簡略化。 三角方程式をさまざまな方法で解く(試験対策)。 11年生。 2012年から2013年。
Kulanin E.D. 数学における 3000 の競技問題。 4番目のID、正解です。 そして追加の – M.: ロルフ、2000 年。
モルドコビッチ A.G. 一般教育学校で三角法を勉強する方法論的な問題 // 学校での数学。 2002年第6号。
ピチュリン L.F. 三角法についてだけではありません: -M. 啓蒙、1985 年
レシェトニコフ N.N. 学校での三角関数: -M. :教育大学「9月1日」、2006年、lk 1。
しゃぶにん M.I.、プロコフィエフ A.A. 数学。 代数。 数学的分析の始まり プロファイル レベル: 10 年生の教科書 - M .: BINOM。 ナレッジラボ、2007 年。
試験準備のための教育ポータル。
数学の受験対策『おお、この三角関数! http://festival.1september.ru/articles/621971/
プロジェクト「数学?簡単!!!」 http://www.resolventa.ru/
セクション: 数学
クラス: 11
レッスン1
主題: 11 年生 (試験の準備)
三角関数式の簡略化。
最も単純な三角方程式の解。 (2時間)
目標:
- 三角関数の公式の使用と最も単純な三角方程式の解法に関する生徒の知識とスキルを体系化し、一般化し、拡張します。
レッスン用の備品:
レッスンの構成:
- 組織
- ラップトップでのテスト。 結果についての議論。
- 三角関数式の簡略化
- 最も単純な三角方程式の解法
- 独立した作品。
- レッスンの概要。 宿題の説明。
1. 組織的な瞬間。 (2分)
教師は聴衆に挨拶し、レッスンの主題を発表し、以前に三角関数の公式を繰り返すという課題が与えられたことを思い出し、生徒たちにテストの準備をさせます。
2. テスト。 (15分+ディスカッション3分)
目標は、三角関数の公式の知識とそれを適用する能力をテストすることです。 各生徒の机にはラップトップがあり、テストのオプションがあります。
オプションはいくつでもありますが、そのうちの 1 つの例を示します。
私はオプションです。
式を簡略化します。
a) 基本的な三角恒等式
1. sin 2 3y + cos 2 3y + 1;
b) 加算式
3. sin5x - sin3x;
c) 積を和に変換する
6. 2sin8y cos3y;
d) 倍角の公式
7.2sin5x cos5x;
e) 半角の公式
f) 三重角の公式
g) 汎用置換
h) 度を下げる
16. cos 2 (3x/7);
生徒は各公式の前でラップトップを使用し、自分の答えを確認します。
作品はすぐにコンピューターでチェックされます。 結果は大きな画面に表示され、誰でも見ることができます。
また、作業終了後には生徒のノートパソコンに正解が表示されます。 各生徒はどこで間違いがあったか、どの公式を繰り返す必要があるかを確認します。
3. 三角関数の式の簡略化。 (25分)
目標は、三角法の基本公式の応用を繰り返し、解決し、定着させることです。 試験の問題 B7 を解きます。
この段階では、クラスを強い生徒(独立して取り組み、その後の検証を行う)と教師と協力する弱い生徒のグループに分けることをお勧めします。
得意な生徒向けの課題(事前に印刷して作成)。 USE 2011 によると、主に強調されるのは縮小と倍角の公式です。
式を簡略化します (強力な学習者向け):

並行して、教師は苦手な生徒と協力し、生徒の口述に従って画面上で話し合い、課題を解決します。
計算します:
5) sin(270° - α) + cos(270° + α)
6) 
簡略化する:

今度は、強力なグループの作業の結果について話し合う番になりました。
回答は画面に表示され、ビデオ カメラの助けを借りて、5 人の異なる生徒の課題が表示されます (それぞれ 1 つの課題)。
弱いグループは状況と解決方法を見ます。 議論と分析があります。 技術的手段を使用すると、これは迅速に行われます。
4. 最も単純な三角方程式の解法。 (30分。)
目標は、最も単純な三角方程式の解を繰り返し、体系化し、一般化し、その根を記録することです。 問題B3の解決策。
どのような三角方程式も、どのように解いても最も単純な方程式に行き着きます。
課題を完了するとき、学生は、特定の場合および一般的な形式の方程式の根を書くこと、および最後の方程式の根の選択に注意を払う必要があります。
方程式を解く:

答えの最小の正の根を書き留めてください。
5. 自主制作(10分)
目標は、習得したスキルをテストし、問題、エラー、およびそれらを除去する方法を特定することです。
学生の希望に応じて、さまざまな仕事が提供されます。
「3」のオプション
1) 式の値を求める ![]()
2) 式 1 - sin 2 3α - cos 2 3α を簡略化します。
3) 方程式を解く ![]()
「4」のオプション
1) 式の値を求める
2) 方程式を解く ![]() 答えの最小の正根を書き留めてください。
答えの最小の正根を書き留めてください。
「5」のオプション
1) 次の場合に tgα を求めます。 ![]()
2) 方程式の根を求める ![]() 答えの最小の正根を書き留めてください。
答えの最小の正根を書き留めてください。
6. レッスンの概要 (5 分)
教師は、レッスンで最も単純な三角方程式の解法である三角関数の公式を繰り返して強化したという事実を要約しました。
宿題(事前にプリントベースで準備)が課され、次のレッスンでスポットチェックが行われます。
方程式を解く:

9) ![]()
10) ![]() 最小の正の根として答えを与えてください。
最小の正の根として答えを与えてください。
レッスン 2
主題: 11 年生 (試験の準備)
三角方程式を解く方法。 ルートの選択。 (2時間)
目標:
- さまざまなタイプの三角方程式を解くための知識を一般化し、体系化します。
- 生徒の数学的思考、観察、比較、一般化、分類する能力の発達を促進します。
- 精神活動の過程で困難を克服し、自制し、自分の活動を内省するよう生徒を励まします。
レッスン用の備品: KRMu、各生徒にラップトップ。
レッスンの構成:
- 組織
- d / sとsamotについてのディスカッション。 前回のレッスンの作品
- 三角方程式を解く方法の繰り返し。
- 三角方程式を解く
- 三角方程式の根の選択。
- 独立した作品。
- レッスンの概要。 宿題。
1. 整理の瞬間 (2 分)
教師は聴衆に挨拶し、レッスンのトピックと作業計画を発表します。
2. a) 宿題の分析 (5 分)
目的はパフォーマンスを確認することです。 ビデオカメラの助けを借りて 1 つの作品が画面に表示され、残りは教師がチェックできるように選択的に収集されます。
b) 独立した作業の分析 (3 分)
目的は、間違いを整理し、それを克服する方法を示すことです。
画面には答えと解決策が表示され、生徒たちは事前に課題を提出しました。 分析は急速に進んでいます。
3. 三角方程式の解き方の繰り返し(5分)
目標は、三角方程式を解く方法を思い出すことです。
生徒たちに、三角方程式を解く方法をどのように知っているか尋ねます。 いわゆる基本的な (頻繁に使用される) メソッドがあることを強調します。
- 変数置換、
- 因数分解、
- 同次方程式、
応用されたメソッドもあります:
- 和を積に、積を和に変換する公式に従って、
- リダクション公式により、
- 普遍的な三角関数の置換
- 補助角度の導入、
- 何らかの三角関数を掛けること。
1 つの方程式はさまざまな方法で解くことができることも思い出してください。
4. 三角方程式を解く(30分)
目標は、このトピックに関する知識とスキルを一般化して統合し、USE から C1 を解決する準備をすることです。
学生と一緒にそれぞれの方法の方程式を解くことが有益であると考えています。
生徒が解答を口述し、教師がタブレットに書き留めると、プロセス全体が画面に表示されます。 これにより、以前に取り上げた内容を記憶にすばやく効率的に復元できるようになります。
方程式を解く:
1) 変数変化 6cos 2 x + 5sinx - 7 = 0
2) 因数分解 3cos(x/3) + 4cos 2 (x/3) = 0
3) 同次方程式 sin 2 x + 3cos 2 x - 2sin2x = 0
4) 合計を積に変換 cos5x + cos7x = cos(π + 6x)
5) 積を合計 2sinx sin2x + cos3x = 0 に変換します。
6)sin2xの次数を下げる - sin 2 2x + sin 2 3x \u003d 0.5
7) 汎用三角関数置換 sinx + 5cosx + 5 = 0。
この方程式を解く際、サインとコサインが tg(x/2) に置き換えられるため、この方法を使用すると定義範囲が狭くなることに注意してください。 したがって、答えを書き出す前に、セット π + 2πn, n Z の数値がこの方程式の馬であるかどうかを確認する必要があります。
8) 補助角の導入 √3sinx + cosx - √2 = 0
9) 何らかの三角関数を掛ける cosx cos2x cos4x = 1/8。
5. 三角方程式の根の選択 (20 分)
大学入学時の熾烈な競争条件では、試験の前半部分の解答だけでは十分ではないため、ほとんどの学生は後半部分(C1、C2、C3)の課題に注意を払う必要があります。
したがって、レッスンのこの段階の目的は、以前に学習した内容を思い出して、2011 年の USE の問題 C1 を解く準備をすることです。
答えを書くときに根を選択する必要がある三角方程式があります。 これは、いくつかの制限によるものです。たとえば、分数の分母はゼロではない、偶数次の根の式は負ではない、対数の符号の式は正などです。
このような方程式は複雑さが増した方程式とみなされ、USE バージョンでは 2 番目の部分、つまり C1 に含まれます。
方程式を解きます。
次の場合、小数はゼロです ![]() 単位円を使用してルートを選択します (図 1 を参照)
単位円を使用してルートを選択します (図 1 を参照)

写真1。
x = π + 2πn、n Z が得られます。
答え: π + 2πn、n Z
画面上では、ルートの選択がカラー画像の円上に表示されます。
因子の少なくとも 1 つがゼロに等しい場合、積はゼロに等しく、同時に円弧はその意味を失いません。 それから

単位円を使用してルートを選択します (図 2 を参照)

セクション: 数学
クラス: 11
レッスン1
主題: 11 年生 (試験の準備)
三角関数式の簡略化。
最も単純な三角方程式の解。 (2時間)
目標:
- 三角関数の公式の使用と最も単純な三角方程式の解法に関する生徒の知識とスキルを体系化し、一般化し、拡張します。
レッスン用の備品:
レッスンの構成:
- 組織
- ラップトップでのテスト。 結果についての議論。
- 三角関数式の簡略化
- 最も単純な三角方程式の解法
- 独立した作品。
- レッスンの概要。 宿題の説明。
1. 組織的な瞬間。 (2分)
教師は聴衆に挨拶し、レッスンの主題を発表し、以前に三角関数の公式を繰り返すという課題が与えられたことを思い出し、生徒たちにテストの準備をさせます。
2. テスト。 (15分+ディスカッション3分)
目標は、三角関数の公式の知識とそれを適用する能力をテストすることです。 各生徒の机にはラップトップがあり、テストのオプションがあります。
オプションはいくつでもありますが、そのうちの 1 つの例を示します。
私はオプションです。
式を簡略化します。
a) 基本的な三角恒等式
1. sin 2 3y + cos 2 3y + 1;
b) 加算式
3. sin5x - sin3x;
c) 積を和に変換する
6. 2sin8y cos3y;
d) 倍角の公式
7.2sin5x cos5x;
e) 半角の公式
f) 三重角の公式
g) 汎用置換
h) 度を下げる
16. cos 2 (3x/7);
生徒は各公式の前でラップトップを使用し、自分の答えを確認します。
作品はすぐにコンピューターでチェックされます。 結果は大きな画面に表示され、誰でも見ることができます。
また、作業終了後には生徒のノートパソコンに正解が表示されます。 各生徒はどこで間違いがあったか、どの公式を繰り返す必要があるかを確認します。
3. 三角関数の式の簡略化。 (25分)
目標は、三角法の基本公式の応用を繰り返し、解決し、定着させることです。 試験の問題 B7 を解きます。
この段階では、クラスを強い生徒(独立して取り組み、その後の検証を行う)と教師と協力する弱い生徒のグループに分けることをお勧めします。
得意な生徒向けの課題(事前に印刷して作成)。 USE 2011 によると、主に強調されるのは縮小と倍角の公式です。
式を簡略化します (強力な学習者向け):

並行して、教師は苦手な生徒と協力し、生徒の口述に従って画面上で話し合い、課題を解決します。
計算します:
5) sin(270° - α) + cos(270° + α)
6) 
簡略化する:

今度は、強力なグループの作業の結果について話し合う番になりました。
回答は画面に表示され、ビデオ カメラの助けを借りて、5 人の異なる生徒の課題が表示されます (それぞれ 1 つの課題)。
弱いグループは状況と解決方法を見ます。 議論と分析があります。 技術的手段を使用すると、これは迅速に行われます。
4. 最も単純な三角方程式の解法。 (30分。)
目標は、最も単純な三角方程式の解を繰り返し、体系化し、一般化し、その根を記録することです。 問題B3の解決策。
どのような三角方程式も、どのように解いても最も単純な方程式に行き着きます。
課題を完了するとき、学生は、特定の場合および一般的な形式の方程式の根を書くこと、および最後の方程式の根の選択に注意を払う必要があります。
方程式を解く:

答えの最小の正の根を書き留めてください。
5. 自主制作(10分)
目標は、習得したスキルをテストし、問題、エラー、およびそれらを除去する方法を特定することです。
学生の希望に応じて、さまざまな仕事が提供されます。
「3」のオプション
1) 式の値を求める ![]()
2) 式 1 - sin 2 3α - cos 2 3α を簡略化します。
3) 方程式を解く ![]()
「4」のオプション
1) 式の値を求める
2) 方程式を解く ![]() 答えの最小の正根を書き留めてください。
答えの最小の正根を書き留めてください。
「5」のオプション
1) 次の場合に tgα を求めます。 ![]()
2) 方程式の根を求める ![]() 答えの最小の正根を書き留めてください。
答えの最小の正根を書き留めてください。
6. レッスンの概要 (5 分)
教師は、レッスンで最も単純な三角方程式の解法である三角関数の公式を繰り返して強化したという事実を要約しました。
宿題(事前にプリントベースで準備)が課され、次のレッスンでスポットチェックが行われます。
方程式を解く:

9) ![]()
10) ![]() 最小の正の根として答えを与えてください。
最小の正の根として答えを与えてください。
レッスン 2
主題: 11 年生 (試験の準備)
三角方程式を解く方法。 ルートの選択。 (2時間)
目標:
- さまざまなタイプの三角方程式を解くための知識を一般化し、体系化します。
- 生徒の数学的思考、観察、比較、一般化、分類する能力の発達を促進します。
- 精神活動の過程で困難を克服し、自制し、自分の活動を内省するよう生徒を励まします。
レッスン用の備品: KRMu、各生徒にラップトップ。
レッスンの構成:
- 組織
- d / sとsamotについてのディスカッション。 前回のレッスンの作品
- 三角方程式を解く方法の繰り返し。
- 三角方程式を解く
- 三角方程式の根の選択。
- 独立した作品。
- レッスンの概要。 宿題。
1. 整理の瞬間 (2 分)
教師は聴衆に挨拶し、レッスンのトピックと作業計画を発表します。
2. a) 宿題の分析 (5 分)
目的はパフォーマンスを確認することです。 ビデオカメラの助けを借りて 1 つの作品が画面に表示され、残りは教師がチェックできるように選択的に収集されます。
b) 独立した作業の分析 (3 分)
目的は、間違いを整理し、それを克服する方法を示すことです。
画面には答えと解決策が表示され、生徒たちは事前に課題を提出しました。 分析は急速に進んでいます。
3. 三角方程式の解き方の繰り返し(5分)
目標は、三角方程式を解く方法を思い出すことです。
生徒たちに、三角方程式を解く方法をどのように知っているか尋ねます。 いわゆる基本的な (頻繁に使用される) メソッドがあることを強調します。
- 変数置換、
- 因数分解、
- 同次方程式、
応用されたメソッドもあります:
- 和を積に、積を和に変換する公式に従って、
- リダクション公式により、
- 普遍的な三角関数の置換
- 補助角度の導入、
- 何らかの三角関数を掛けること。
1 つの方程式はさまざまな方法で解くことができることも思い出してください。
4. 三角方程式を解く(30分)
目標は、このトピックに関する知識とスキルを一般化して統合し、USE から C1 を解決する準備をすることです。
学生と一緒にそれぞれの方法の方程式を解くことが有益であると考えています。
生徒が解答を口述し、教師がタブレットに書き留めると、プロセス全体が画面に表示されます。 これにより、以前に取り上げた内容を記憶にすばやく効率的に復元できるようになります。
方程式を解く:
1) 変数変化 6cos 2 x + 5sinx - 7 = 0
2) 因数分解 3cos(x/3) + 4cos 2 (x/3) = 0
3) 同次方程式 sin 2 x + 3cos 2 x - 2sin2x = 0
4) 合計を積に変換 cos5x + cos7x = cos(π + 6x)
5) 積を合計 2sinx sin2x + cos3x = 0 に変換します。
6)sin2xの次数を下げる - sin 2 2x + sin 2 3x \u003d 0.5
7) 汎用三角関数置換 sinx + 5cosx + 5 = 0。
この方程式を解く際、サインとコサインが tg(x/2) に置き換えられるため、この方法を使用すると定義範囲が狭くなることに注意してください。 したがって、答えを書き出す前に、セット π + 2πn, n Z の数値がこの方程式の馬であるかどうかを確認する必要があります。
8) 補助角の導入 √3sinx + cosx - √2 = 0
9) 何らかの三角関数を掛ける cosx cos2x cos4x = 1/8。
5. 三角方程式の根の選択 (20 分)
大学入学時の熾烈な競争条件では、試験の前半部分の解答だけでは十分ではないため、ほとんどの学生は後半部分(C1、C2、C3)の課題に注意を払う必要があります。
したがって、レッスンのこの段階の目的は、以前に学習した内容を思い出して、2011 年の USE の問題 C1 を解く準備をすることです。
答えを書くときに根を選択する必要がある三角方程式があります。 これは、いくつかの制限によるものです。たとえば、分数の分母はゼロではない、偶数次の根の式は負ではない、対数の符号の式は正などです。
このような方程式は複雑さが増した方程式とみなされ、USE バージョンでは 2 番目の部分、つまり C1 に含まれます。
方程式を解きます。
次の場合、小数はゼロです ![]() 単位円を使用してルートを選択します (図 1 を参照)
単位円を使用してルートを選択します (図 1 を参照)

写真1。
x = π + 2πn、n Z が得られます。
答え: π + 2πn、n Z
画面上では、ルートの選択がカラー画像の円上に表示されます。
因子の少なくとも 1 つがゼロに等しい場合、積はゼロに等しく、同時に円弧はその意味を失いません。 それから

単位円を使用してルートを選択します (図 2 を参照)

図2。
5) ![]()
システムに行きましょう:
![]()
システムの最初の方程式で、log 2 (sinx) = y を変更し、次の方程式を取得します。 ![]() 、システムに戻ります
、システムに戻ります
単位円を使用してルートを選択します (図 5 を参照)。

図5

6. 自主制作(15分)
目標は、素材の同化を統合して確認し、エラーを特定し、それらを修正する方法の概要を示すことです。
この作品は、生徒の選択に応じて、事前に印刷ベースで作成された 3 つのバージョンで提供されます。
方程式はどのような方法でも解くことができます。
「3」のオプション
方程式を解く:
1) 2sin 2 x + sinx - 1 = 0
2) sin2x = √3cosx
「4」のオプション
方程式を解く:
1) cos2x = 11sinx - 5
2) (2sinx + √3)log 8 (cosx) = 0
「5」のオプション
方程式を解く:
1) 2sinx - 3cosx = 2
2) ![]()
7. レッスンのまとめ、宿題(5分)
教師はレッスンを総括し、三角方程式はいくつかの方法で解くことができるという事実にもう一度注意を促しました。 迅速に結果を達成するための最良の方法は、特定の生徒が最もよく学ぶ方法です。
試験の準備をするときは、公式や方程式の解き方を体系的に繰り返す必要があります。
宿題(事前に印刷して作成したもの)が配布され、いくつかの方程式の解き方が解説されます。
方程式を解く:
1) cosx + cos5x = cos3x + cos7x
2) 5sin(x/6) - cos(x/3) + 3 = 0
3) 4sin 2x + sin2x = 3
4) sin 2 x + sin 2 2x - sin 2 3x - sin 2 4x = 0
5) cos3x cos6x = cos4x cos7x
6) 4sinx - 6cosx = 1
7) 3sin2x + 4 cos2x = 5
8) cosx cos2x cos4x cos8x = (1/8) cos15x
9) (2sin 2 x - sinx)log 3 (2cos 2 x + cosx) = 0
10) (2cos 2 x - √3cosx)log 7 (-tgx) = 0
11) ![]()
で 同一の変換 三角関数の式次の代数トリックを使用できます。同一の項の加算と減算。 括弧内の共通因数を取り除きます。 同じ値による乗算と除算。 省略された乗算公式の適用。 完全な正方形の選択。 平方三項式の因数分解。 変換を簡素化するための新しい変数の導入。
分数を含む三角関数式を変換する場合、比例、分数の約分、または分数の公分母への約分などのプロパティを使用できます。 さらに、分数の整数部分の選択を使用して、分数の分子と分母に同じ値を乗算することもできます。また、可能であれば、分子または分母の一様性を考慮することもできます。 必要に応じて、分数をいくつかの単純な分数の合計または差として表すことができます。
さらに、三角関数式を変換するために必要なすべての方法を適用するときは、変換された式の許容値の範囲を常に考慮する必要があります。
いくつかの例を見てみましょう。
例1
A = (sin (2x - π) cos (3π - x) + sin (2x - 9π/2) cos (x + π/2)) 2 + (cos (x - π/2) cos ( 2x – 7π) を計算します。 /2) +
+
sin (3π/2 - x) sin (2x -5π/2))2
解決。
リダクション公式から次のことがわかります。
sin (2x - π) \u003d -sin 2x; cos (3π - x) \u003d -cos x;
sin (2x - 9π / 2) \u003d -cos 2x; cos (x + π/2) = -sin x;
cos (x - π / 2) \u003d sin x; cos (2x - 7π/2) = -sin 2x;
sin (3π / 2 - x) \u003d -cos x; sin (2x - 5π / 2) \u003d -cos 2x。
ここから、引数の加算の公式と基本的な三角関数恒等式により、次の結果が得られます。
A \u003d (sin 2x cos x + cos 2x sin x) 2 + (-sin x sin 2x + cos x cos 2x) 2 \u003d sin 2 (2x + x) + cos 2 (x + 2x) \u003d
= sin 2 3x + cos 2 3x = 1
答え: 1.
例 2
M = cos α + cos (α + β) cos γ + cos β – sin (α + β) sin γ + cos γ の式を積に変換します。
解決。
引数の加算式と三角関数の和を積に変換する式を適切にグループ化すると、次のようになります。
М = (cos (α + β) cos γ - sin (α + β) sin γ) + cos α + (cos β + cos γ) =
2cos ((β + γ)/2) cos ((β – γ)/2) + (cos α + cos (α + β + γ)) =
2cos ((β + γ)/2) cos ((β – γ)/2) + 2cos (α + (β + γ)/2) cos ((β + γ)/2)) =
2cos ((β + γ)/2) (cos ((β – γ)/2) + cos (α + (β + γ)/2)) =
2cos ((β + γ)/2) 2cos ((β – γ)/2 + α + (β + γ)/2)/2) cos ((β – γ)/2) – (α + ( β + γ)/2)/2) =
4cos((β+γ)/2)cos((α+β)/2)cos((α+γ)/2)。
答え: М = 4cos ((α + β)/2) cos ((α + γ)/2) cos ((β + γ)/2)。
例 3.
式 A \u003d cos 2 (x + π / 6) - cos (x + π / 6) cos (x - π / 6) + cos 2 (x - π / 6) が R のすべての x を 1 つとることを示します。と同じ値です。 この値を見つけてください。
解決。
この問題を解決するための 2 つの方法を紹介します。 最初の方法を適用し、完全な正方形を分離し、対応する基本的な三角関数の公式を使用すると、次の結果が得られます。
A \u003d (cos (x + π / 6) - cos (x - π / 6)) 2 + cos (x - π / 6) cos (x - π / 6) \u003d
4sin 2 x sin 2 π/6 + 1/2(cos 2x + cos π/3) =
sin 2 x + 1/2 cos 2x + 1/4 = 1/2 (1 - cos 2x) + 1/2 cos 2x + 1/4 = 3/4。
2 番目の方法で問題を解くと、A を R からの x の関数とみなして、その導関数を計算します。 変換後、次のようになります。
А´ \u003d -2cos (x + π/6) sin (x + π/6) + (sin (x + π/6) cos (x - π/6) + cos (x + π/6) sin ( x + π/6)) - 2cos (x - π/6) sin (x - π/6) =
sin 2(x + π/6) + sin ((x + π/6) + (x - π/6)) - sin 2(x - π/6) =
sin 2x - (sin (2x + π/3) + sin (2x - π/3)) =
sin 2x - 2sin 2x cos π/3 = sin 2x - sin 2x ≡ 0。
したがって、区間で微分可能な関数の不変性の基準により、次のように結論付けられます。
A(x) ≡ (0) = cos 2 π/6 - cos 2 π/6 + cos 2 π/6 = (√3/2) 2 = 3/4、x ∈ R。 
答え: A = 3/4 for x € R.
三角関数の恒等性を証明する主な方法は次のとおりです。
A)適切な変換によるアイデンティティの左側の右側への縮小。
b)アイデンティティの右側を左側に縮小します。
V)アイデンティティの右部分と左部分を同じ形式に縮小する。
G)証明される同一性の左部分と右部分の差がゼロになること。
例 4
cos 3x = -4cos x cos (x + π/3) cos (x + 2π/3) であることを確認します。
解決。
この恒等式の右辺を、対応する三角関数の公式に従って変換すると、次のようになります。
4cos x cos (x + π/3) cos (x + 2π/3) =
2cos x (cos ((x + π/3) + (x + 2π/3)) + cos ((x + π/3) – (x + 2π/3))) =
2cos x (cos (2x + π) + cos π/3) =
2cos x cos 2x - cos x = (cos 3x + cos x) - cos x = cos 3x。
アイデンティティの右側は左側に縮小されます。
例5
α、β、γ が三角形の内角である場合、sin 2 α + sin 2 β + sin 2 γ – 2cos α cos β cos γ = 2 であることを証明します。
解決。
α、β、γ が三角形の内角であることを考慮すると、次のことが得られます。
α + β + γ = π したがって、γ = π – α – βとなります。
sin 2 α + sin 2 β + sin 2 γ – 2cos α cos β cos γ =
sin 2 α + sin 2 β + sin 2 (π - α - β) - 2cos α cos β cos (π - α - β) =
sin 2 α + sin 2 β + sin 2 (α + β) + (cos (α + β) + cos (α - β) (cos (α + β) =
sin 2 α + sin 2 β + (sin 2 (α + β) + cos 2 (α + β)) + cos (α - β) (cos (α + β) =
1/2 (1 - cos 2α) + 1/2 (1 - cos 2β) + 1 + 1/2 (cos 2α + cos 2β) = 2
元の等価性が証明されます。
例6
三角形の角度 α、β、γ のいずれかが 60°に等しくなるためには、sin 3α + sin 3β + sin 3γ = 0 であることが必要かつ十分であることを証明します。
解決。
この問題の条件は、必要性と十分性の両方の証明を前提としています。
まず証明します 必要性.
それは次のことを示すことができます
sin 3α + sin 3β + sin 3γ = -4cos (3α/2) cos (3β/2) cos (3γ/2)
したがって、cos (3/2 60°) = cos 90° = 0 を考慮すると、角度 α、β、または γ の 1 つが 60° に等しい場合、次のようになります。
cos (3α/2) cos (3β/2) cos (3γ/2) = 0 なので、sin 3α + sin 3β + sin 3γ = 0 となります。
今すぐ証明しましょう 十分性指定された条件。
sin 3α + sin 3β + sin 3γ = 0 の場合、cos (3α/2) cos (3β/2) cos (3γ/2) = 0 となるため、
cos (3α/2) = 0、cos (3β/2) = 0、または cos (3γ/2) = 0 のいずれかです。
したがって、
または 3α/2 = π/2 + πk、つまり α = π/3 + 2πk/3、 
または 3β/2 = π/2 + πk、つまり β = π/3 + 2πk/3、
または 3γ/2 = π/2 + πk、
それらの。 γ = π/3 + 2πk/3、ここで k ϵ Z。
α、β、γ が三角形の角度であるという事実から、次のようになります。
0 < α < π, 0 < β < π, 0 < γ < π.
したがって、α = π/3 + 2πk/3 または β = π/3 + 2πk/3 または
γ = π/3 + 2πk/3 すべての kϵZ のうち k = 0 のみが適合します。
したがって、α = π/3 = 60°、β = π/3 = 60°、または γ = π/3 = 60°のいずれかになります。
その主張は証明されました。
何か質問がありますか? 三角関数の式を簡略化する方法がわかりませんか?
家庭教師のサポートを受けるには、登録してください。
初回レッスンは無料です!
サイトにコンテンツを完全または部分的にコピーする場合は、ソースへのリンクが必要です。


