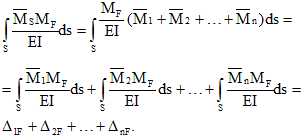Calcola un sistema di aste piatte staticamente indeterminato. Calcolo di sistemi staticamente indeterminati con il metodo delle forze

I sistemi staticamente indeterminati sono detti sistemi a stelo, per determinare le reazioni di appoggi in cui non bastano solo le equazioni di equilibrio. Da un punto di vista cinematico, si tratta di tali sistemi di aste, il cui numero di gradi di libertà è inferiore al numero di legami. Per rivelare l'indeterminatezza statica di tali sistemi, è necessario comporre ulteriori equazioni di compatibilità della deformazione. Il numero di tali equazioni è determinato dal numero di indeterminatezza statica del sistema di aste. La Figura 8.14 mostra esempi di travi e telai staticamente indeterminati.

Viene chiamata la trave mostrata in Fig. 8.14b continuo trave. Questo nome deriva dal fatto che il supporto intermedio supporta solo la trave. Nel punto di appoggio, la trave non viene tagliata da una cerniera, la cerniera non viene tagliata nel corpo della trave. Pertanto, l'influenza delle sollecitazioni e delle deformazioni che la trave subisce sulla campata sinistra influisce anche sulla campata destra. Se una cerniera viene tagliata nel corpo della trave al posto del supporto intermedio, di conseguenza il sistema diventerà staticamente determinato - da una trave otterremo due travi indipendenti l'una dall'altra, ognuna delle quali sarà staticamente determinata . Va notato che le travi continue sono meno materiche rispetto alle travi divise, poiché distribuiscono più razionalmente i momenti flettenti lungo la loro lunghezza. A questo proposito, le travi continue sono ampiamente utilizzate nell'edilizia e nell'ingegneria. Tuttavia, le travi continue, essendo staticamente indeterminate, richiedono una tecnica di calcolo speciale, che prevede l'uso di deformazioni del sistema.

Prima di procedere al calcolo dei sistemi staticamente indeterminati, è necessario imparare a determinare il grado della loro indeterminazione statica. Una delle regole più semplici per determinare il grado di indeterminazione statica è la seguente:

, (8.3)

dove  numero dei titoli obbligazionari imposti alla struttura;  il numero di possibili equazioni di equilibrio indipendenti che possono essere compilate per il sistema in esame.

Usiamo l'equazione (8.3) per determinare il grado di indeterminazione statica dei sistemi mostrati nella Figura 8.14.

La trave mostrata nella Figura 8.14a è una volta staticamente indeterminata, poiché ha tre legature sulla gamba sinistra e una legatura sulla gamba destra. Ci sono solo tre equazioni di equilibrio indipendenti per un tale raggio. Pertanto, il grado di indeterminazione statica del raggio
. Anche la trave continua mostrata in Fig. 8.14b è una volta staticamente indeterminata, poiché ha due collegamenti sul supporto sinistro e un collegamento ciascuno sul supporto intermedio e sul supporto destro - per un totale di quattro collegamenti. Quindi, il grado della sua indeterminazione statica
.

Il telaio mostrato in fig. 8.14c, è tre volte staticamente indeterminato, poiché ha sei legami nei supporti. Ci sono solo tre equazioni di equilibrio indipendenti per questo frame. Pertanto, il grado di incertezza statica per questo frame dall'equazione (8.3) è:
. Il grado di indeterminazione statica del telaio mostrato in Fig. 8.18, d è pari a quattro, poiché il telaio ha sette connessioni sui supporti. Pertanto, il grado della sua indeterminazione statica è uguale a
.

La regola (8.3) per determinare il grado di indeterminazione statica è usata solo per i sistemi semplici. Nei casi più complessi, questa regola non funziona. La Figura 8.15 mostra un frame il cui grado di incertezza statica non può essere determinato usando l'equazione (8.3).

Esternamente, il sistema mostrato nella Figura 8.15 è cinque volte staticamente indeterminato. Questo è facile da stabilire usando l'equazione (8.3): da sei legami esterni (tre nella sezione A, tre nella sezione B e due nella sezione C), vengono sottratte tre possibili equazioni di equilibrio. Tuttavia, questo sistema ha anche un'indeterminazione statica interna. È impossibile tenere conto dell'indeterminazione statica interna usando l'equazione (8.3). Prima di passare alla determinazione del grado di indeterminazione statica del frame mostrato in Figura 8.15, introduciamo alcune definizioni. La prima di queste definizioni include la nozione di cerniera semplice.

Semplice chiamato cerniera di collegamento tra due aste (Fig. 8.16).

Fig.8.16. cerniera semplice

Viene chiamata una cerniera che collega più aste difficile(Fig.8.17).

Fig.8.17. cerniera complessa

Il numero di cerniere semplici che possono sostituire una cerniera complessa è determinato dalla formula:

, (8.4)

dove
- il numero di aste comprese nel nodo.

Ricalcoliamo il cardine complesso mostrato in Fig. 8.17 nel numero di cardini semplici usando la formula (8.4):
. Pertanto, il cardine complesso mostrato nella Figura 8.17 può essere sostituito da quattro cardini semplici.

Introduciamo un altro concetto - ciclo chiuso.

Dimostriamo il teorema: qualsiasi anello chiuso è tre volte staticamente indeterminato.

Per dimostrare il teorema, si consideri un circuito chiuso carico di forze esterne (Fig.8.18).

Tagliamo un contorno chiuso con una sezione verticale e mostriamo i fattori di forza interni che sorgono nel sito della sezione. In ciascuna delle sezioni sorgono tre fattori interni: la forza di taglio , momento flettente
e forza longitudinale
. In totale, ciascuna delle parti tagliate del contorno, oltre alle forze esterne, è influenzata da sei fattori interni (Fig. 8.18, b, c). Considerando l'equilibrio di una delle parti tagliate, ad esempio quella di sinistra (Fig. 8.18, b), scopriamo che il problema è tre volte staticamente indeterminato, poiché per il taglio possono essere compilate solo tre equazioni di equilibrio indipendenti -off, e ci sono sei forze sconosciute che agiscono sulla parte cut-off. Pertanto, il grado di indeterminazione statica di un anello chiuso è uguale a
. Il teorema è stato dimostrato.

Ora, utilizzando il concetto di cerniera semplice e anello chiuso, possiamo formulare un'altra regola per determinare il grado di indeterminazione statica:

, (8.5)

dove
 numero di anelli chiusi;
 numero di cerniere in termini di semplici (8.4).

Usando l'equazione (8.5), determiniamo il grado di indeterminatezza statica del frame mostrato nella Figura 8.15. Il telaio ha cinque contorni
, compreso il contorno formato dalle aste di supporto. La cerniera al nodo D è semplice, in quanto collega due aste. La cerniera nella sezione K è complessa, in quanto collega quattro tiranti. Il numero di cerniere semplici che potrebbero sostituire la cerniera nella sezione K è, secondo la formula (8.4):
. Anche la cerniera C è complessa in quanto collega tre aste. Per questa cerniera
. Inoltre, il sistema dispone di due cerniere più semplici, con le quali si aggancia alla base. Pertanto, il numero di cardini semplici nel sistema è
. Sostituendo il numero di anelli chiusi
e il numero di cerniere semplici
nella formula (8.5) determiniamo il grado di indeterminazione statica del frame:
. Pertanto, mostrato in Fig. 8.15 frame, sette volte staticamente indeterminato. E questo significa che per calcolare un tale sistema è necessario comporre, oltre alle tre equazioni di equilibrio, sette equazioni di compatibilità delle deformazioni. Risolvendo il sistema di 10 equazioni così ottenuto rispetto alle incognite incluse in queste equazioni, è possibile determinare sia l'entità delle reazioni nei legami esterni che le forze interne che si generano nel frame. La procedura per risolvere questo problema può essere alquanto semplificata escludendo le equazioni di equilibrio dal sistema di equazioni. Tuttavia, questo approccio richiede l'uso di metodi di soluzione speciali, uno dei quali è il metodo della forza.

I sistemi sono chiamati staticamente indeterminati in cui le forze interne non possono essere determinate solo da equazioni di equilibrio (equazioni statiche).

Le costruzioni staticamente indeterminate hanno le cosiddette superfluo connessioni. Possono verificarsi in supporti, aste e altri elementi. Tali connessioni sono dette "superflue" perché non sono necessarie per garantire l'equilibrio della struttura, ma sono determinate dai requisiti per la sua resistenza e rigidità. Tali connessioni extra vengono chiamate esterno. Inoltre, potrebbero sorgere connessioni non necessarie a causa delle caratteristiche del design stesso. Ad esempio, un contorno del telaio chiuso (Fig. 46, G) ha tre forze interne sconosciute in ciascuna sezione, cioè solo sei, e tre di loro sono "extra". Questo sforzo extra è chiamato interno. A seconda del numero di connessioni "extra" esterne o interne, stabiliscono il grado di indeterminazione statica del sistema.È uguale alla differenza tra il numero di incognite da determinare e il numero di equazioni statiche. Con un "extra" sconosciuto, il sistema viene chiamato una volta, o una volta staticamente indeterminato, con due - due volte staticamente indeterminato, ecc.

Il disegno mostrato in fig. 46, un, è una volta staticamente indeterminato, e le costruzioni mostrate nelle Figg. 46, b e in, - doppiamente staticamente indeterminato, in Fig. 46, d - tre volte con un costrutto staticamente indeterminato.

Quando si risolvono problemi staticamente indeterminati, oltre alle equazioni statiche, vengono utilizzate equazioni che tengono conto delle deformazioni degli elementi strutturali.

Esistono diversi metodi per risolvere problemi staticamente indeterminati: metodo di confronto degli spostamenti, metodo delle forze, metodo degli spostamenti.

metodo della forza

Quando si calcolano sistemi staticamente indeterminati, le forze sono considerate incognite.

Calcolo per metodo della forza effettuata nella seguente sequenza:

• 1. Impostare il grado di incertezza statica.
• 2. Eliminando i collegamenti "extra", il sistema originario viene sostituito da uno staticamente determinato, denominato sistema principale. Diversi di questi sistemi possono essere costruiti, osservando le condizioni del loro geo

immutabilità metrica.

• 3. Il sistema principale è caricato con determinate forze esterne e forze "extra" sconosciute che sostituiscono l'azione delle connessioni remote, risultando in sistema equivalente.
• 4. Per garantire l'equivalenza tra il sistema originario e quello principale, le forze incognite devono essere scelte in modo che le deformazioni del sistema principale non differiscano dalle deformazioni del sistema originario staticamente indeterminato. A tal fine, lo spostamento dei punti di applicazione delle incognite "superflue" nella direzione della loro azione è pari a zero. Dalle equazioni aggiuntive ottenute in questo modo, vengono determinati i valori delle forze sconosciute "extra". La determinazione degli spostamenti dei punti corrispondenti può essere fatta in qualsiasi modo, ma è meglio utilizzare il metodo Mohr più generale.
• 5. Dopo aver determinato i valori delle forze sconosciute "extra", vengono determinate le reazioni e vengono tracciati i diagrammi delle forze interne, le sezioni vengono selezionate e la forza viene verificata nel solito modo.

Equazioni canoniche del metodo delle forze

Ulteriori equazioni di spostamento che esprimono l'uguaglianza a zero degli spostamenti nelle direzioni di incognite "extra" possono essere convenientemente compilate nel cosiddetto forma canonica quelli. secondo un certo schema. Mostriamo questo con l'esempio di risolvere il più semplice sistema staticamente indeterminato (Fig. 47, un).

Scegliamo la console come sistema principale, scartando il supporto articolato. Il sistema equivalente si otterrà dopo l'applicazione della sua forza esterna T 7 e dell'incognita "extra". X(Fig. 47, b).

Equazione canonica, che esprime lo spostamento zero del punto A dalle forze F e X, sarà

Dall'equazione che abbiamo

Per un sistema che ha due connessioni "extra", il sistema di equazioni canoniche ha la forma:

• 8 11 X 1 + b 12 ^2 + ^1
• 621-^1 + 622^2 "Io" ^20-

Movimenti A[pag E b [y, inclusi nelle equazioni canoniche, sono determinati dal metodo di Mohr.

Per i sistemi costituiti da elementi rettilinei, è conveniente calcolare gli spostamenti utilizzando il metodo Vereshchagin.

Ad esempio, per il compito rappresentato in Fig. 47, moltiplicando i diagrammi (Fig. 48), otteniamo i coefficienti dell'equazione canonica:

1 2 io 3 1 io / io 2 1 5 I1 3

E]L LL =-/ / -/ = -, E]LA LR =-------- +-------.

1 11 2 3 3 1 1R 2 2 2 2 3 2/ 48 E]

Ottenere Chl - - = - e.

Definire la forza X, abbiamo effettivamente trovato la reazione di supporto Sono dentro. Inoltre, il problema della determinazione dei fattori di forza interni può essere risolto, come di consueto, utilizzando il metodo delle sezioni.

MINISTERO DELL'EDUCAZIONE DELLA FEDERAZIONE RUSSA

ISTITUZIONE STATALE

UNIVERSITÀ TECNICA STATALE DI KUZBAS

Dipartimento di Forza dei Materiali

CALCOLO DI SISTEMI A CERNIERA-ASTA STATICAMENTE INDETERMINATI IN TENSIONE - COMPRESSIONE

Linee guida per l'implementazione del calcolo e del compito grafico sulla forza dei materiali per studenti di tutte le specialità

Compilato da: V.D. Moiseenko

Approvato nella riunione di dipartimento il Verbale n. 8 del 29.06.01

Una copia elettronica si trova nella biblioteca dell'edificio principale del KuzGTU

Kemerovo 2002

Introduzione. Scopo e finalità dell'incarico

Un sistema cerniera-asta staticamente indeterminato è quello in cui le forze nelle aste e le reazioni nei supporti non possono essere determinate solo dalla condizione di equilibrio.

La figura 1 mostra una staffa convenzionale composta da due aste. Le forze N 1 e N 2 nelle aste di questa staffa sono facilmente determinate dalla condizione di equilibrio per il sistema di forze convergenti applicato al nodo tagliato C, poiché sono risolte due equazioni per questo sistema di forze con due incognite.

Se il progetto della staffa è complicato aggiungendo un'altra asta (Fig. 1, b), le forze nelle aste non possono essere determinate allo stesso modo, poiché per il nodo C è ancora possibile compilare solo due equazioni di equilibrio statico (ΣХ = 0; ΣY = 0), e il numero di forze sconosciute è tre. Abbiamo una volta un sistema staticamente indeterminato.

Complicando il progetto e introducendo nuove aste, si può ottenere un sistema staticamente indeterminato due volte (vedi Fig. 1c), tre volte e così via. Pertanto, per n volte un sistema staticamente indeterminato si intende un sistema in cui il numero di connessioni supera il numero di equazioni indipendenti della statica di n unità.

Ulteriori equazioni necessarie per risolvere il problema possono essere trovate considerando il sistema in uno stato deformato e stabilendo collegamenti tra spostamenti e deformazioni degli elementi strutturali. Le equazioni risultanti sono chiamate equazioni di compatibilità delle deformazioni.

La figura 2 mostra i diagrammi di alcuni sistemi staticamente indeterminati.

Fig.2. Alcuni tipi di sistemi staticamente indeterminati

Durante lo studio della sezione "Sistemi di aste staticamente indeterminati" e l'esecuzione di questo compito di calcolo e grafico, lo studente deve apprendere le caratteristiche dei sistemi staticamente indeterminati; acquisire abilità nella rivelazione dell'indeterminatezza statica, nel determinare le forze negli elementi strutturali e nella selezione delle aree trasversali dalla condizione di resistenza.

Il compito prevede che lo studente esegua quanto segue:

- determinare le forze nelle aste e selezionare le aree della sezione trasversale dall'azione dei carichi esterni;

- determinare ulteriori sollecitazioni nelle aste dovute agli sbalzi di temperatura;

- determinare ulteriori sollecitazioni di montaggio causate da imprecisioni nella fabbricazione delle aste;

- selezionare le sezioni delle aste in base allo stato limite.

Il volume e la forma di esecuzione del calcolo e del compito grafico dipendono dal volume del corso oggetto di studio e sono negoziati dall'insegnante nelle classi pratiche.

1. Brevi informazioni teoriche

Quando si risolvono problemi staticamente indeterminati, è necessario seguire il seguente ordine:

1.1. Considera il lato statico del problema. Costruisci un piano delle forze e scrivi le equazioni della statica.

1.2. Considera il lato geometrico del problema. Costruisci un piano di viaggio. Compilare ulteriori equazioni di compatibilità della deformazione in una quantità tale da poter trovare tutte le forze sconosciute.

1.3. Considera il lato fisico del problema. Secondo le leggi della fisica (con calcolo della temperatura) e secondo la legge di Hooke, esprimiamo le deformazioni nelle equazioni della loro compatibilità attraverso forze sconosciute agenti nelle aste:

1.4. Produrre una soluzione congiunta delle equazioni di statica, geometria, fisica e determinare le forze sconosciute.

1.5. Utilizzo di condizioni di resistenza alla compressione o alla trazione N/F = [ σ ], selezionare le aree della sezione trasversale delle aste.

1.6. Con forze note nelle aste e aree della sezione trasversale accettate, calcolare le sollecitazioni normali utilizzando la formula

σ = N F .

2. Esempio

Dato: una trave AB assolutamente rigida poggia, come mostrato in Fig. 3, caricata con un carico e una forza P uniformemente distribuiti.

Fig.3. Schema di un sistema staticamente indeterminato

Dati iniziali per il calcolo

4. Determinare le sollecitazioni totali nelle aste dall'azione di carichi, variazioni di temperatura e imprecisioni di fabbricazione.

2.1. Calcolo di un sistema di aste incernierate staticamente indeterminato per carico esterno

P = 30 kN q = 15 kN/m

A C B

Fig.4. Schema di progettazione iniziale

2.1.1. Il lato statico del problema

Il lato statico del problema è considerato dal piano delle forze. Il piano delle forze è uno schema progettuale che mostra tutte le forze (sia note che sconosciute) applicate all'elemento del sistema di aste incernierate, di cui si considera l'equilibrio (nel nostro caso si tratta di una trave rigida AB). Tagliamo le barre di acciaio e rame e sostituiamo le loro parti inferiori scartate con forze interne (Fig. 5).

P = 30 kN q = 15 kN/m

A C B

60°

Riso. 5. Piano delle forze da carichi esterni

Dal piano delle forze (vedi Fig. 5) scriviamo le equazioni di equilibrio statico. Per rispondere alla prima domanda del problema, è necessario conoscere le forze nelle aste: acciaio e rame. In questo caso non è necessario calcolare la reazione del supporto incernierato. Quindi su tre

possibili equazioni di statica (ΣX = 0; ΣY = 0 ; Σm c = 0 ) scriviamo

uno che non include le reazioni del supporto fisso C:

∑ mC = 0

− N CT a + q a 2 2 + p a + NM sin60o b = 0,

− N ST 2 + 15 2 2 2 + 30 2 − NM 0,866 4 = 0,

Dopo le operazioni algebriche, l'equazione di equilibrio assumerà la forma

2.1.2. Il lato geometrico del problema

Il lato geometrico del problema è considerato dal piano di spostamento. Il piano di spostamento è un diagramma di progetto che mostra la posizione del sistema di aste incernierate prima e dopo il carico. Sul piano di spostamento indichiamo gli spostamenti dei punti della trave (AA1 e BB1),

deformazioni assolute delle barre di rame e acciaio (∆ l ST ; ∆ l M )

(Fig. 6). Inoltre, a causa di piccole deformazioni, spostiamo i punti della trave verticalmente verso l'alto o verso il basso e segniamo le deformazioni delle aste inclinate con una perpendicolare.

Riso. 6. Piano degli spostamenti dall'azione dei carichi esterni

Secondo il piano di spostamento, elaboriamo un'equazione per la compatibilità delle deformazioni. Prima di tutto, scriviamo il rapporto tra gli spostamenti dei punti della trave dalla somiglianza dei triangoli AA1 C e CBB1 (Fig. 6):

Gli spostamenti dei punti della trave (AA1 e BB1) sono espressi in termini di deformazioni

Le espressioni (2.3) e (2.4) sono sostituite nella relazione (2.2):

2.1.3. Il lato fisico del problema

L'equazione di compatibilità della deformazione risultante (2.5) in questa forma non può essere risolta con l'equazione di equilibrio (2.1), perché le incognite in esse incluse sono di natura diversa.

Deformazioni assolute ∆ l CT e ∆ l M nell'equazione (2.5) esprimiamo

Abbiamo ottenuto l'equazione di compatibilità della deformazione scritta in termini di forze nelle aste.

2.1.4. Sintesi

Risolviamo insieme le equazioni di equilibrio (2.1) e l'equazione di compatibilità delle deformazioni (2.6).

NCT + 1,73 NM = 45

0,67NCT \u003d 0,95NM.

Dalla seconda equazione del sistema, esprimiamo la forza N ST:

e sostituisci nella prima equazione del sistema.

Il risultato positivo di N ST e N M conferma le nostre ipotesi di compressione della barra di acciaio e tensione della barra di rame, il che significa che le forze nelle barre saranno:

2.1.5. Selezione delle sezioni trasversali delle barre

La selezione delle sezioni trasversali delle aste viene effettuata in base alla condizione di resistenza alla trazione - compressione:

N F ≤ [σ] .

a) Sarà determinata l'area della sezione trasversale della barra d'acciaio richiesta dalla condizione di resistenza:

b) Sarà determinata l'area della sezione trasversale della barra di rame richiesta dalla condizione di resistenza:

In questo caso, in base al rapporto di aree indicato, l'area della barra d'acciaio dovrebbe essere uguale a:

FCT = 4 3 FM = 4 3 1.7 10- 4 = 1.275 10- 4 m2 ..

Accettiamo grandi sezioni trasversali delle aste:

Con le aree della sezione trasversale accettate delle barre di rame e acciaio, determiniamo le sollecitazioni in queste barre.

2.2. Calcolo della temperatura di un sistema cerniera-asta staticamente indeterminato

Lo scopo del calcolo della temperatura è determinare le sollecitazioni aggiuntive nelle barre di rame e acciaio dovute alle variazioni di temperatura.

Supponiamo che il sistema sia riscaldato di ∆ t = 20 o C . L'algoritmo di soluzione rimane lo stesso. Lo schema di progettazione iniziale è mostrato in fig. 7.

Vengono chiamati sistemi di aste in cui le reazioni di supporto e i fattori di forza interni non possono essere trovati dalle sole equazioni di equilibrio staticamente indeterminato.

Determina la differenza tra il numero di forze sconosciute richieste e le equazioni di equilibrio indipendenti grado di indeterminazione statica del sistema. Il grado di indeterminazione statica è sempre uguale al numero di connessioni ridondanti (superflue), la cui rimozione trasforma un sistema staticamente indeterminato in un sistema staticamente determinabile geometricamente invariabile. Sia i collegamenti esterni (di riferimento) che quelli interni, che impongono determinate restrizioni al movimento delle sezioni del sistema l'uno rispetto all'altro, possono essere ridondanti.

Geometricamente invariabile si chiama un tale sistema, il cui cambio di forma è possibile solo in connessione con le deformazioni dei suoi elementi.

Geometricamente variabile viene chiamato un tale sistema, i cui elementi possono muoversi sotto l'azione di forze esterne senza deformazioni (meccanismo).

Mostrato in fig. 12.1 il frame ha sette collegamenti esterni (di supporto). Per determinare le forze in questi legami (reazioni di supporto), è possibile comporre solo tre equazioni di equilibrio indipendenti. Pertanto, questo sistema ha quattro connessioni ridondanti, il che significa che è quattro volte staticamente indeterminato. Pertanto, il grado di incertezza statica per i telai piatti è:

dove R- numero di reazioni di supporto.

Un contorno costituito da un numero di elementi (dritti o curvilinei) rigidamente (senza cardini) collegati tra loro e che formano un circuito chiuso è chiamato circuito chiuso. . La cornice rettangolare mostrata nella Figura 12.2 è un anello chiuso. È tre volte staticamente indeterminato, poiché per renderlo staticamente indeterminato è necessario tagliare uno dei suoi elementi ed eliminare tre connessioni extra. Le reazioni di questi legami sono: forza longitudinale, forza trasversale e momento flettente agenti nel punto di taglio; non possono essere determinati usando le equazioni della statica. In condizioni simili, nel senso di indeterminatezza statica, c'è un anello chiuso, che è sempre tre volte staticamente indeterminato.

L'inserimento di una cerniera in un nodo di telaio in cui convergono due aste, o il posizionamento in qualsiasi punto dell'asse dell'asta, rimuove un collegamento e riduce di uno il grado di indeterminazione statica complessiva. Tale cerniera è chiamata singola o semplice (Fig. 12.3).

In generale, ogni cerniera inclusa in un nodo di connessione c aste, riduce il grado di incertezza statica di c-1 , poiché tale cerniera sostituisce c-1 cerniere singole (Fig. 12.3). Pertanto, il grado di indeterminazione statica del sistema in presenza di anelli chiusi è determinato dalla formula.

Un tale sistema è detto staticamente indeterminato se non può essere calcolato usando le sole equazioni della statica, poiché ha connessioni non necessarie. Per calcolare tali sistemi, vengono compilate equazioni aggiuntive che tengono conto delle deformazioni del sistema.

Sistemi staticamente indeterminati hanno una serie di caratteristiche:

1. staticamente indeterminato le strutture sono più rigide delle corrispondenti staticamente determinato, poiché hanno connessioni aggiuntive.
2. In staticamente indeterminato sistemi, ci sono forze interne minori, che determinano la loro efficienza rispetto a staticamente determinato sistemi sotto gli stessi carichi esterni.
3. Violazione di connessioni non necessarie in staticamente indeterminato sistema non sempre porta alla distruzione, mentre la perdita di comunicazione in staticamente determinato sistema lo rende geometricamente variabile.
4. Per il calcolo staticamente indeterminato sistemi, è necessario specificare preliminarmente le caratteristiche geometriche delle sezioni trasversali degli elementi, ovvero infatti, la loro forma e dimensione, poiché il loro mutamento porta a un mutamento delle forze nelle connessioni ea una nuova distribuzione degli sforzi in tutti gli elementi del sistema.
5. Durante il calcolo staticamente indeterminato sistemi, è necessario selezionare in anticipo il materiale di costruzione, poiché è necessario conoscerne i moduli di elasticità.
6. In staticamente indeterminato sistemi, effetti della temperatura, assestamento dei supporti, imprecisioni nella produzione e nell'installazione comportano ulteriori sforzi.

Principale metodi di calcolostaticamente indeterminato i sistemi sono:

1. metodo della forza. Qui, le forze sono considerate incognite: forze e momenti.
2.Metodo di movimento. Sconosciuti sono i fattori di deformazione: angoli di rotazione e spostamenti lineari.
3.metodo misto. Qui, parte delle incognite rappresenta gli sforzi e l'altra parte rappresenta gli spostamenti.
4. Metodo combinato. Viene utilizzato nel calcolo di sistemi simmetrici per carichi asimmetrici. Si scopre che è consigliabile calcolare il sistema per la componente simmetrica di un determinato carico con il metodo dello spostamento e per la componente inversamente simmetrica - con il metodo della forza.
Oltre ai metodi analitici indicati, nel calcolo di sistemi particolarmente complessi vengono utilizzati diversi metodi numerici.

Equazioni canoniche del metodo delle forze

Per ottenere equazioni aggiuntive, di cui si è parlato nel paragrafo precedente, devi prima di tutto girare quella data, n volte staticamente indeterminato sistema in uno staticamente determinato rimuovendo da esso le connessioni non necessarie. Viene chiamato il sistema staticamente determinato risultante di base. Si noti che la trasformazione di un dato sistema in uno staticamente determinato non è obbligatoria. A volte viene utilizzata una modifica del metodo della forza in cui può essere il sistema sottostante staticamente indeterminato, tuttavia, la presentazione di questo problema esula dagli scopi di questo manuale. L'eliminazione di eventuali legami non modifica le forze interne e le deformazioni del sistema se ad esso vengono applicate forze e momenti aggiuntivi, che sono le reazioni dei legami scartati. Ciò significa che se un determinato carico e le reazioni dei collegamenti remoti vengono applicati al sistema principale, diventeranno i sistemi principali e dati equivalente.

In un dato sistema non possono esserci spostamenti lungo le direzioni dei collegamenti rigidi esistenti, compresi quei collegamenti che vengono scartati durante il passaggio al sistema principale, pertanto, nel sistema principale, gli spostamenti lungo le direzioni dei collegamenti scartati devono essere uguale a zero. E per questo, le reazioni delle obbligazioni cadute devono avere valori rigorosamente definiti.

La condizione di uguaglianza a zero di spostamento in direzione di un qualsiasi i-esimo collegamento su n scartato sulla base del principio di indipendenza dell'azione delle forze ha la forma:

dove il primo indice indica la direzione del movimento e il numero della connessione caduta, e il secondo indica il motivo che ha causato il movimento, ad es. è il movimento nella direzione dell'i-esimo legame, causato dalla reazione del k-esimo legame; - movimento nella direzione della i-esima connessione, causato dall'azione contemporanea dell'intero carico esterno.

Nel metodo delle forze, la reazione del k-esimo legame è solitamente indicata con Xk. Tenendo conto di questa designazione e data la validità della legge di Hooke, gli spostamenti possono essere rappresentati come:

dove è un movimento singolo (o specifico) nella direzione dell'i-esimo legame, causato dalla reazione cioè reazione coincidente in direzione con Xk, ma uguale all'unità.

Sostituendo (2) in (1), otteniamo:

significato fisico equazione (3): il movimento nel sistema principale nella direzione della i-esima connessione scartata è uguale a zero.

Scrivendo espressioni simili a (3) per l'intero insieme di legami scartati, otteniamo sistema di equazioni canonichemetodo della forza:

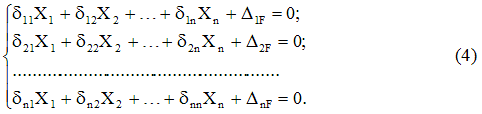
La forma dell'equazione (4), cioè il numero di termini in ciascuno di essi e il loro numero totale è determinato solo dal grado di indeterminazione statica del sistema e non dipende dalle sue caratteristiche specifiche.

I coefficienti del sistema di equazioni canoniche (4) sono determinati dal metodo di Mohr-Vereshchagin moltiplicando i diagrammi corrispondenti. Tutti questi coefficienti, come detto sopra, rappresentano spostamenti; i coefficienti che stanno alle incognite sono spostamenti unitari e lo sono i membri liberi carico. I singoli movimenti sono divisi in principale, situato lungo la diagonale principale e avente gli stessi indici e effetti collaterali(). I movimenti principali sono sempre positivi, a differenza di quelli laterali. Gli spostamenti posizionati simmetricamente, secondo il teorema sulla reciprocità degli spostamenti, sono uguali tra loro, cioè .

Algoritmo per il calcolo del metodo delle forze

Indipendentemente dalle caratteristiche del progetto considerato, si può distinguere la seguente sequenza di calcolo di sistemi staticamente indeterminati metodo della forza:

1. Determina grado di incertezza statica.
2. Selezionare il sistema principale.
3. Formare un sistema equivalente.
4. Masterizzare il sistema equazioni canoniche.
5. Costruire unità e diagrammi di carico dei fattori di forza interni che si verificano negli elementi della struttura considerata.
6. Calcolare i coefficienti delle incognite ei termini liberi del sistema di equazioni canoniche.
7. Costruisci un diagramma singolo totale.
8. Eseguire un controllo universale dei coefficienti per termini sconosciuti e liberi.
9. Risolvi il sistema (4), cioè determinare le reazioni di legami extra.
10. Costruire diagrammi di fattori di forza interni emergenti per un dato sistema (in altre parole, diagrammi finali).
11. Eseguire controlli statici e cinematici.
Si noti che i punti 7, 8, 11 dell'algoritmo di cui sopra non sono assolutamente necessari, sebbene consentano di controllare la correttezza del calcolo. E per i sistemi con una connessione in più, i punti 7 e 8 sono semplicemente privi di significato, poiché in questo caso il diagramma singolo totale coincide con quello singolo.
Diamo un'occhiata più da vicino ad alcuni dei passaggi di calcolo precedenti.

La scelta di un sistema primario

Questa è la fase più importante del calcolo, poiché la scelta razionale del sistema principale semplifica notevolmente il lavoro di calcolo. Consideriamo possibili modi per rimuovere le connessioni non necessarie, che determinano la forma del sistema principale.

1. Il rifiuto dei collegamenti non necessari avviene mediante la rimozione completa di alcuni supporti o la loro sostituzione con supporti con un numero inferiore di collegamenti. Le reazioni che agiscono nelle direzioni dei legami caduti sono incognite ridondanti. La figura 1, b, c, d mostra varie versioni del sistema equivalente ottenuto con questo metodo per il telaio (figura 1, a).

2. Il posizionamento delle cerniere nelle sezioni intermedie delle aste consente in ciascuna di tali sezioni di stabilire un collegamento corrispondente al momento flettente. Questi momenti sono incognite superflue. Per un telaio con un grado di indeterminazione statica n = 3 (Fig. 2, a), quando si sceglie il sistema principale, è necessario installare tre cerniere. La posizione di queste cerniere può essere arbitraria, ma soddisfa il requisito dell'invariabilità geometrica del sistema (Fig. 2b).

3. La dissezione dell'asta elimina tre legami corrispondenti alle forze interne M, Q, N (Fig. 2, c). In casi particolari (Fig. 2d), il taglio di un'asta lungo una cerniera rilascia due legami (Fig. 2, e) e il taglio di un'asta diritta con cardini alle estremità rilascia un legame (Fig. 2, f).

Tra le connessioni di un sistema staticamente indeterminato si distinguono assolutamente necessarie e condizionatamente necessarie. Assolutamente necessari sono i collegamenti, una volta rimossi i quali il sistema diventa geometricamente mutevole. Una connessione assolutamente necessaria è caratterizzata dalla determinabilità statica dello sforzo in essa contenuto, ad es. la reazione di un tale legame può essere calcolata dalla condizione di equilibrio. Nella scelta del sistema principale non si possono scartare le connessioni assolutamente necessarie.

Le relazioni, alla rimozione delle quali il sistema continua a rimanere geometricamente invariato, sono dette condizionalmente necessarie. Un sistema che è stato scollegato potrebbe essere il sistema principale metodo della forza.

Calcolo di coefficienti e termini liberi di equazioni canoniche

Questa fase del calcolo è preceduta dalla costruzione di diagrammi unitari e di carico dei fattori di forza interni (per travi e telai - diagrammi dei momenti flettenti). I diagrammi unitari sono costruiti dall'azione di una forza unitaria adimensionale o di un momento unitario adimensionale, coincidente in direzione con la direzione del corrispondente eccesso sconosciuto nel sistema equivalente, e sono indicati da , e il diagramma unitario - da .

Il diagramma di carico è costruito dal carico esterno applicato al sistema principale. In questo caso è possibile costruire un diagramma dall'azione simultanea di tutti i carichi esterni o più diagrammi, separatamente da ciascuno dei carichi applicati. Tale divisione di un diagramma di carico in più semplici, di norma, è consigliabile solo quando tra i carichi esistenti ce n'è uno uniformemente distribuito e il diagramma dei momenti nella sezione corrispondente sotto di esso è alternato di segni. In questo caso, in ciascuna equazione canonica, il numero di termini liberi sarà uguale al numero di diagrammi di carico tracciati.

Gli spostamenti unitari e di carico (coefficienti e termini liberi delle equazioni canoniche) possono essere generalmente calcolati con il metodo di Mohr. Per travi e telai, questo può essere fatto usando la regola di Vereshchagin.

Verifica universale dei coefficienti e termini liberi delle equazioni canoniche

Per eseguire un controllo universale, è necessario costruire un diagramma dell'unità totale, un diagramma dei momenti dall'azione simultanea di tutte le forze unitarie applicate al sistema principale:

Moltiplichiamo il diagramma singolo totale per il diagramma:

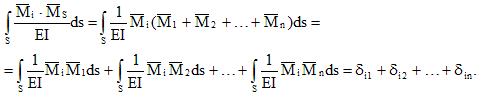
Pertanto, il risultato della moltiplicazione del totale e dell'i-esimo diagramma singolo è un movimento nella direzione dell'i-esimo collegamento dall'azione congiunta di singole incognite extra. Questo spostamento è uguale alla somma dei coefficienti dell'i-esima equazione canonica:

Questo controllo viene chiamato linea per linea e vale per ogni equazione canonica.
Invece di controlli su n righe, ne viene spesso eseguito uno - controllo universale, che consiste nel moltiplicare per sé il diagramma delle unità totali e nel verificare la condizione:

Se viene eseguito il controllo universale, gli spostamenti delle unità vengono calcolati correttamente; in caso contrario, è necessario eseguire dei controlli riga per riga, che consentiranno di chiarire lo spostamento, durante il calcolo del quale è stato commesso un errore.

Per verificare gli spostamenti di carico è necessario moltiplicare l'unità totale e i diagrammi di carico dei momenti flettenti:

Pertanto, la verifica dei termini liberi del sistema di equazioni canoniche (4) consiste nel soddisfacimento della condizione.