Limiti in matematica per manichini: spiegazione, teoria, esempi di soluzioni. Risolvere i limiti scoprendo le incertezze Numero fino al potere infinito negativo
LEZIONE 20
20.1 DIVULGAZIONE DELL'INCERTEZZA SULLA SPECIE
Esempio 1
Limite di risoluzione 
Innanzitutto, proviamo a sostituire -1 nella frazione: 
In questo caso si ottiene la cosiddetta incertezza.
Regola generale: se il numeratore e il denominatore contengono polinomi e c'è incertezza sulla forma, allora rivelarlo devi fattorizzare il numeratore e il denominatore.
Per fare ciò, molto spesso è necessario risolvere un'equazione quadratica e/o utilizzare formule di moltiplicazione abbreviate.
Fattorizziamo il numeratore. 
Esempio 2
Calcola limite 
Fattorizziamo il numeratore e il denominatore.
Numeratore denominatore: 
,
Metodo per moltiplicare il numeratore e il denominatore per l'espressione coniugata
Continuiamo a considerare l'incertezza della forma
Il tipo successivo di limiti è simile al tipo precedente. L'unica cosa, oltre ai polinomi, aggiungeremo le radici.
Esempio 3
Trova il limite 
Moltiplicare il numeratore e il denominatore per l'espressione coniugata.
20.2 DIVULGAZIONE DELL'INCERTEZZA SULLA SPECIE
Considereremo ora il gruppo dei limiti quando , e la funzione è una frazione il cui numeratore e denominatore contengono polinomi
Esempio 4
Calcola limite 
Secondo la nostra regola, proveremo a sostituire l'infinito nella funzione. Cosa otteniamo in cima? Infinito. E cosa succede sotto? Anche l'infinito. Abbiamo quindi quella che viene chiamata incertezza della specie. Si potrebbe pensare che la risposta sia pronta, ma nel caso generale non è affatto così, ed è necessario applicare qualche tecnica risolutiva, che ora considereremo.
Come risolvere limiti di questo tipo?
Per prima cosa guardiamo il numeratore e troviamo la potenza più alta: 
La potenza principale al numeratore è due.
Ora guardiamo il denominatore e troviamolo anche alla massima potenza: 
Il grado più alto del denominatore è due.
Quindi scegliamo la potenza più alta del numeratore e del denominatore: in questo esempio sono uguali e uguali a due.
Quindi, il metodo di soluzione è il seguente: per rivelare l’incertezzadevi dividere numeratore e denominatore pernel grado senior.
Dividi numeratore e denominatore per 
Eccola, la risposta, e non l'infinito.
Cosa è di fondamentale importanza nella progettazione di una decisione?
Innanzitutto, indichiamo l’incertezza, se presente.
In secondo luogo è consigliabile interrompere la soluzione per spiegazioni intermedie. Di solito uso il segno, non ha alcun significato matematico, ma significa che la soluzione viene interrotta per una spiegazione intermedia.
In terzo luogo, è consigliabile contrassegnare al limite cosa sta andando e dove. Quando il lavoro è redatto a mano, è più conveniente farlo in questo modo: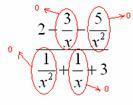 
È meglio usare una matita semplice per gli appunti.
Naturalmente, non devi fare nulla di tutto ciò, ma poi, forse, l'insegnante indicherà i difetti della soluzione o inizierà a porre ulteriori domande sul compito. Ne hai bisogno?
Esempio 5
Trova il limite 
Sempre al numeratore e al denominatore troviamo in massimo grado: 
Grado massimo al numeratore: 3 Grado massimo al denominatore: 4 Selezionare più grande valore, in questo caso quattro. Secondo il nostro algoritmo, per rivelare l'incertezza, dividiamo il numeratore e il denominatore per. L'incarico completo potrebbe assomigliare a questo:
Esempio 6
Trova il limite 
Grado massimo di “X” al numeratore: 2 Grado massimo di “X” al denominatore: 1 (può essere scritto come) Per rivelare l'incertezza, è necessario dividere il numeratore e il denominatore per. La soluzione finale potrebbe assomigliare a questa:
Dividi numeratore e denominatore per
Notazione non significa divisione per zero (non si può dividere per zero), ma divisione per un numero infinitesimo.
Pertanto, scoprendo l’incertezza sulle specie, potremmo essere in grado di farlo numero finale, zero o infinito.
PRATICA 20
COMPITO N1
Soluzione: Se al posto della variabile mettiamo il valore 7 a cui tende, allora otteniamo un'incertezza della forma 
COMPITO N2Argomento: Informativa sull'incertezza del tipo “da zero a zero”.
Soluzione: Se al posto di una variabile mettiamo il valore 0 a cui tende, allora otteniamo l'incertezza della forma
COMPITO N 3Argomento: Informativa sull'incertezza del tipo “da zero a zero”.
Soluzione: Se al posto della variabile mettiamo il valore 6 a cui tende, allora otteniamo un'incertezza della forma
COMPITO N.4
Soluzione: Perché 
E 
COMPITO N5Argomento: Divulgazione dell'incertezza della forma "dall'infinito all'infinito"
Soluzione: Perché 
E 
allora c'è incertezza della forma e per rivelarla è necessario dividere ogni termine del numeratore e del denominatore per. Quindi, sapendo cosa otteniamo: 
LAVORO INDIPENDENTE 20
COMPITO N1Argomento: Informativa sull'incertezza del tipo “da zero a zero”.
COMPITO N2Argomento: Informativa sull'incertezza del tipo “da zero a zero”.
COMPITO N 3Argomento: Informativa sull'incertezza del tipo “da zero a zero”.
COMPITO N.4Argomento: Divulgazione dell'incertezza della forma "dall'infinito all'infinito"
COMPITO N5Argomento: Divulgazione dell'incertezza della forma "dall'infinito all'infinito" Limite di funzione 
pari...
COMPITO N6Argomento: Divulgazione dell'incertezza della forma "dall'infinito all'infinito"
La derivata della funzione non cade lontano, e nel caso delle regole di L'Hopital cade esattamente nello stesso punto in cui cade la funzione originaria. Questa circostanza aiuta a rivelare incertezze della forma 0/0 o ∞/∞ e alcune altre incertezze che sorgono durante il calcolo limite la relazione tra due funzioni infinitesime o infinitamente grandi. Il calcolo è notevolmente semplificato utilizzando questa regola (in realtà due regole e relative note):
Come mostra la formula sopra, quando si calcola il limite del rapporto tra due funzioni infinitesime o infinitamente grandi, il limite del rapporto tra due funzioni può essere sostituito dal limite del rapporto tra le loro derivati e quindi ottenere un certo risultato.
Passiamo a formulazioni più precise delle regole di L'Hopital.
Regola di L'Hopital per il caso del limite di due quantità infinitesime. Passiamo alle funzioni F(X) E G(X UN. E proprio nel punto UN UN derivata di una funzione G(X) non è zero ( G"(X UN sono uguali tra loro e pari a zero:
.
Regola di L'Hopital per il caso del limite di due quantità infinitamente grandi. Passiamo alle funzioni F(X) E G(X) hanno derivate (cioè differenziabili) in qualche intorno del punto UN. E proprio nel punto UN potrebbero non avere derivati. Inoltre, in prossimità del punto UN derivata di una funzione G(X) non è zero ( G"(X)≠0) e i limiti di queste funzioni poiché x tende al valore della funzione nel punto UN sono uguali tra loro e uguali all'infinito:
.
Allora il limite del rapporto di queste funzioni è uguale al limite del rapporto delle loro derivate:
In altri termini, per incertezze della forma 0/0 o ∞/∞, il limite del rapporto tra due funzioni è uguale al limite del rapporto delle loro derivate, se quest'ultima esiste (finita, cioè uguale a certo numero, o infinito, cioè uguale a infinito).
Appunti.
1. Le regole de L'Hopital si applicano anche quando le funzioni F(X) E G(X) non sono definiti quando X = UN.
2. Se, quando si calcola il limite del rapporto tra le derivate delle funzioni F(X) E G(X) arriviamo nuovamente a un'incertezza della forma 0/0 o ∞/∞, allora le regole di L'Hôpital dovrebbero essere applicate ripetutamente (almeno due volte).
3. Le regole di L'Hopital sono applicabili anche quando l'argomento delle funzioni (x) non tende a un numero finito UN e all'infinito ( X → ∞).
Anche le incertezze di altro tipo possono essere ridotte a incertezze del tipo 0/0 e ∞/∞.
Divulgazione delle incertezze del tipo “zero diviso per zero” e “infinito diviso per infinito”
Esempio 1.
X=2 porta ad un'incertezza della forma 0/0. Pertanto si ottiene la derivata di ciascuna funzione
La derivata del polinomio è stata calcolata al numeratore e al denominatore - derivata di una funzione logaritmica complessa. Prima dell'ultimo segno di uguale, il solito limite, sostituendo un due invece di una X.
Esempio 2. Calcola il limite del rapporto tra due funzioni utilizzando la regola di L'Hopital:
Soluzione. Sostituzione di un valore in una determinata funzione X
Esempio 3. Calcola il limite del rapporto tra due funzioni utilizzando la regola di L'Hopital:
Soluzione. Sostituzione di un valore in una determinata funzione X=0 porta ad un'incertezza della forma 0/0. Pertanto, calcoliamo le derivate delle funzioni al numeratore e al denominatore e otteniamo:
Esempio 4. Calcolare
Soluzione. Sostituendo il valore x uguale a più infinito in una data funzione si ottiene un'incertezza della forma ∞/∞. Applichiamo quindi la regola di L'Hopital:
Commento. Passiamo agli esempi in cui la regola di L'Hopital deve essere applicata due volte, cioè arrivare al limite del rapporto delle derivate seconde, poiché il limite del rapporto delle derivate prime è un'incertezza della forma 0 /0 o ∞/∞.
Divulgazione delle incertezze della forma "zero volte infinito"
Esempio 12. Calcolare
.
Soluzione. Noi abbiamo
In questo esempio viene utilizzata l'identità trigonometrica.
Divulgazione delle incertezze del tipo "zero alla potenza di zero", "infinito alla potenza di zero" e "uno alla potenza dell'infinito"
Le incertezze della forma , o vengono solitamente ridotte alla forma 0/0 o ∞/∞ prendendo il logaritmo di una funzione della forma
Per calcolare il limite di un'espressione, è necessario utilizzare l'identità logaritmica, un caso speciale della quale è proprietà del logaritmo 
.
Utilizzando l'identità logaritmica e la proprietà di continuità di una funzione (per superare il segno limite), il limite dovrebbe essere calcolato come segue:
Separatamente, dovresti trovare il limite dell'espressione nell'esponente e costruire e al grado trovato.
Esempio 13.
Soluzione. Noi abbiamo
.
.
Esempio 14. Calcola utilizzando la regola di L'Hopital
Soluzione. Noi abbiamo
Calcolare il limite di un'espressione in esponente
.
.
Esempio 15. Calcola utilizzando la regola di L'Hopital
Questa incertezza è “servita” secondo meraviglioso limite, e nella seconda parte di quella lezione abbiamo esaminato in dettaglio esempi standard di soluzioni che si trovano nella pratica nella maggior parte dei casi. Ora il quadro con gli esponenti sarà completato, inoltre, i compiti finali della lezione saranno dedicati ai limiti “falsi”, in cui SEMBRA che sia necessario applicare il 2° limite meraviglioso, sebbene questo non sia affatto il caso.
Lo svantaggio delle due formule di lavoro per il 2° limite notevole è che l’argomento deve tendere a “più infinito” o a zero. Ma cosa succede se l’argomento tende a un numero diverso?
Una formula universale viene in soccorso (che in realtà è una conseguenza del secondo limite notevole):
L’incertezza può essere eliminata utilizzando la formula:
Da qualche parte penso di aver già spiegato cosa significano le parentesi quadre. Niente di speciale, le parentesi sono solo parentesi. Di solito vengono utilizzati per evidenziare più chiaramente la notazione matematica.
Evidenziamo i punti essenziali della formula:
1) Si tratta solo certezze e nient'altro.
2) L'argomento "x" può tendere a valore arbitrario(e non solo a zero o), in particolare, a “meno infinito” o a chiunque numero finito.
Usando questa formula puoi risolvere tutti gli esempi della lezione. Limiti meravigliosi, che appartengono al 2° limite notevole. Ad esempio, calcoliamo il limite:
In questo caso 
, e secondo la formula 
:
È vero, non consiglio di farlo; la tradizione è di utilizzare ancora il design “solito” della soluzione, se applicabile. Tuttavia utilizzando la formula è molto comodo verificare esempi "classici" fino al 2° limite notevole.
Tutto questo è buono e corretto, ma ora ci sono scatti più interessanti nell'inquadratura:
Esempio 18
Calcola limite 
Come primo passo, non mi stancherò di ripeterlo, sostituiamo il valore “x” nell'espressione sotto il segno limite. E se non ci fosse alcuna incertezza? Succede! Ma non in questo momento. Sostituendo il “tre”, arriviamo alla conclusione che qui c’è incertezza
Usiamo la formula
Per non trascinare con sé la lettera “e” e per non rimpicciolirla, l'indicatore 
È più conveniente calcolare separatamente:
In questo caso: 
Così:
Dal punto di vista della tecnologia di calcolo, tutto è routine: prima riduciamo il primo termine a un denominatore comune, poi eliminiamo le costanti ed effettuiamo riduzioni, eliminando l'incertezza 0:0.
Di conseguenza: 
Regalo promesso con differenza logaritmica e incertezza:
Esempio 19
Calcola limite
Prima la soluzione completa, poi i commenti: 
(1)-(2) Nei primi due passaggi utilizziamo le formule 
. U derivati complessi noi “cadiamo a pezzi” i logaritmi, ma qui, al contrario, devono essere “assemblati”.
(3) Spostare l'icona del limite sotto il logaritmo. Questo può essere fatto perché questo logaritmo continuo a "meno infinito". Inoltre, il limite si riferisce al “riempimento” del logaritmo.
(4)-(5) Tecnica standard discussa nella lezione base su limiti meravigliosi, trasformiamo l'incertezza nella forma .
(6) Usiamo la formula .
(7) Le funzioni esponenziale e logaritmica sono funzioni reciprocamente inverse, quindi sia “e” che il logaritmo possono essere rimossi. Infatti, secondo la proprietà del logaritmo: . Aggiungiamo il meno prima della frazione al denominatore: 
(8) Nessun commento =)
La tipologia di limite considerata non è così rara; ho trovato 30-40 esempi.
Esempio 20
Calcola limite 
Questo è un esempio che puoi risolvere da solo. Oltre a utilizzare la formula, puoi rappresentare il limite come 
e mediante la sostituzione riducono la soluzione del caso 
.
In conclusione, diamo un’occhiata ai limiti “falsi”.
Torniamo all'incertezza. Questa incertezza non sempre può essere ridotto all'incertezza e utilizzare il secondo limite notevole o formula di corollario. La trasformazione è fattibile se numeratore e denominatore della base - equivalente funzioni infinitamente grandi. Per esempio: .
Prendiamo una pausa dall'indicatore e calcoliamo il limite della base: 
Nel limite ottenuto unità, che significa numeratore e denominatore non solo dello stesso ordine di crescita, ma anche equivalenti. Alla lezione Limiti notevoli. Esempi di soluzioni Abbiamo facilmente ridotto questo esempio all'incertezza e abbiamo ottenuto la risposta.
Puoi trovare molti limiti simili:
eccetera.
Le frazioni di questi esempi sono accomunate dalla caratteristica di cui sopra: . In altri casi, se c'è incertezza Il 2° limite notevole non è applicabile.
Esempio 21
Trova i limiti
Non importa quanto ci provi, l’incertezza non può essere trasformata in incertezza
Ecco i numeratori e i denominatori delle basi stesso ordine di crescita, ma non equivalente: 
.
Pertanto, il secondo limite notevole e, soprattutto la formula, NON PUÒ ESSERE APPLICATO.
! Nota: Da non confondere con l'Esempio n. 18, in cui il numeratore e il denominatore della base non sono equivalenti. C’è un’incertezza già pronta, ma qui stiamo parlando di incertezza.
Il metodo per risolvere i limiti “falsi” è semplice e semplice: servono un numeratore e un denominatore motivi dividere per “x” al grado più alto (indipendentemente dall'esponente):
Se il numeratore e il denominatore della base hanno un ordine di crescita diverso, la soluzione è esattamente la stessa:
Esempio 22
Trova i limiti 
Questi sono brevi esempi per lo studio autonomo
A volte potrebbe non esserci alcuna incertezza:
Tali trucchi sono particolarmente amati dai compilatori della collezione di Kuznetsov. Ecco perché è molto importante sostituire SEMPRE la “x” nell'espressione sotto il segno limite nel primo passaggio!
Esempio 2
Grado maggiore del numeratore: 2; massimo grado del denominatore: 3.
:
Esempio 4
Dividi numeratore e denominatore per :
Nota
: l'ultima azione è stata moltiplicare il numeratore e il denominatore per per eliminare l'irrazionalità nel denominatore.
Esempio 6
Dividi numeratore e denominatore per :
Esempio 8
Dividi numeratore e denominatore per :
Nota
: termine tendono a zero più lentamente di , Ecco perché è lo zero “principale” del denominatore.
.
Esempio 22
Nota
: funzione infinitesima tende a zero più lentamente di , quindi lo zero “più grande” del denominatore gioca un ruolo decisivo:
I limiti creano molti problemi a tutti gli studenti di matematica. Per risolvere un limite, a volte è necessario utilizzare molti trucchi e scegliere tra una varietà di metodi di soluzione esattamente quello adatto per un particolare esempio.
In questo articolo non ti aiuteremo a comprendere i limiti delle tue capacità o a comprendere i limiti del controllo, ma proveremo a rispondere alla domanda: come comprendere i limiti nella matematica superiore? La comprensione arriva con l'esperienza, quindi allo stesso tempo forniremo diversi esempi dettagliati di risoluzione dei limiti con spiegazioni.
Il concetto di limite in matematica
La prima domanda è: qual è questo limite e il limite di cosa? Possiamo parlare dei limiti delle sequenze e delle funzioni numeriche. A noi interessa il concetto di limite di una funzione, poiché è ciò che gli studenti incontrano più spesso. Ma prima, la definizione più generale di limite:
Diciamo che c'è qualche valore variabile. Se questo valore nel processo di cambiamento si avvicina illimitatamente a un certo numero UN , Quello UN – il limite di questo valore.
Per una funzione definita in un certo intervallo f(x)=y tale numero è chiamato limite UN , a cui tende la funzione quando X , tendente ad un certo punto UN . Punto UN appartiene all'intervallo su cui è definita la funzione.
Sembra complicato, ma è scritto in modo molto semplice:
Lim- dall'inglese limite- limite.
Esiste anche una spiegazione geometrica per determinare il limite, ma qui non approfondiremo la teoria, poiché siamo più interessati al lato pratico piuttosto che a quello teorico della questione. Quando lo diciamo X tende ad un certo valore, ciò significa che la variabile non assume il valore di un numero, ma si avvicina ad esso infinitamente vicino.
Facciamo un esempio specifico. Il compito è trovare il limite.
Per risolvere questo esempio, sostituiamo il valore x=3 in una funzione. Noi abbiamo:
A proposito, se sei interessato alle operazioni di base sulle matrici, leggi un articolo separato su questo argomento.
Negli esempi X può tendere a qualsiasi valore. Può essere qualsiasi numero o infinito. Ecco un esempio quando X tende all'infinito:
Intuitivamente, maggiore è il numero al denominatore, minore sarà il valore che assumerà la funzione. Quindi, con una crescita illimitata X Senso 1/x diminuirà e si avvicinerà allo zero.
Come puoi vedere, per risolvere il limite è sufficiente sostituire nella funzione il valore a cui tendere X . Tuttavia, questo è il caso più semplice. Spesso trovare il limite non è così ovvio. Nei limiti ci sono incertezze del tipo 0/0 O infinito/infinito . Cosa fare in questi casi? Ricorri ai trucchi!
Incertezze dentro
Incertezza della forma infinito/infinito
Lasciamo che ci sia un limite:
Se proviamo a sostituire l'infinito nella funzione, otterremo l'infinito sia al numeratore che al denominatore. In generale, vale la pena dire che c'è un certo elemento artistico nel risolvere tali incertezze: bisogna notare come è possibile trasformare la funzione in modo tale che l'incertezza scompaia. Nel nostro caso dividiamo numeratore e denominatore per X nel grado senior. Cosa accadrà?
Dall'esempio già discusso sopra sappiamo che i termini contenenti x al denominatore tenderanno a zero. Allora la soluzione al limite è:
Per risolvere le incertezze sul tipo infinito/infinito dividi numeratore e denominatore per X al massimo grado.
A proposito! Per i nostri lettori ora c'è uno sconto del 10% su qualsiasi tipo di lavoro
Altro tipo di incertezza: 0/0
Come sempre, sostituendo i valori nella funzione x=-1 dà 0 al numeratore e al denominatore. Guarda un po' più da vicino e noterai che abbiamo un'equazione quadratica al numeratore. Troviamo le radici e scriviamo:
Riduciamo e otteniamo:
Quindi, se ti trovi di fronte all'incertezza del tipo 0/0 – Fattorizzare numeratore e denominatore.
Per facilitare la risoluzione degli esempi, presentiamo una tabella con i limiti di alcune funzioni:
Il governo dell'Hopital all'interno
Un altro modo efficace per eliminare entrambi i tipi di incertezza. Qual è l'essenza del metodo?
Se c'è incertezza nel limite, prendi la derivata del numeratore e del denominatore finché l'incertezza scompare.
La regola di L'Hopital è la seguente:
Punto importante : il limite in cui devono esistere le derivate del numeratore e del denominatore invece del numeratore e del denominatore.
E ora - un esempio reale:
C'è una tipica incertezza 0/0 . Prendiamo le derivate del numeratore e del denominatore:
Voilà, l'incertezza viene risolta in modo rapido ed elegante.
Ci auguriamo che tu possa applicare utilmente queste informazioni nella pratica e trovare la risposta alla domanda "come risolvere i limiti nella matematica superiore". Se devi calcolare il limite di una sequenza o il limite di una funzione in un punto e non c'è assolutamente tempo per questo lavoro, contatta un servizio studenti professionale per una soluzione rapida e dettagliata.
Solitamente il secondo limite notevole si scrive in questa forma:
\begin(equazione) \lim_(x\to\infty)\left(1+\frac(1)(x)\right)^x=e\end(equazione)
Il numero $e$ indicato a destra dell'uguaglianza (1) è irrazionale. Il valore approssimativo di questo numero è: $e\ approx(2(,)718281828459045)$. Se effettuiamo la sostituzione $t=\frac(1)(x)$, la formula (1) può essere riscritta come segue:
\begin(equazione) \lim_(t\to(0))\biggl(1+t\biggr)^(\frac(1)(t))=e\end(equazione)
Per quanto riguarda il primo limite notevole, non ha importanza quale espressione stia al posto della variabile $x$ nella formula (1) o al posto della variabile $t$ nella formula (2). La cosa principale è soddisfare due condizioni:
- La base del grado (cioè l'espressione tra parentesi delle formule (1) e (2)) dovrebbe tendere all'unità;
- L'esponente (cioè $x$ nella formula (1) o $\frac(1)(t)$ nella formula (2)) deve tendere all'infinito.
Si dice che il secondo limite notevole riveli l'incertezza di $1^\infty$. Tieni presente che nella formula (1) non specifichiamo di quale infinito ($+\infty$ o $-\infty$) stiamo parlando. In ognuno di questi casi, la formula (1) è corretta. Nella formula (2), la variabile $t$ può tendere a zero sia a sinistra che a destra.
Noto che ci sono anche diverse conseguenze utili dal secondo limite notevole. Esempi dell'uso del secondo limite notevole, così come le sue conseguenze, sono molto popolari tra i compilatori di calcoli e test standard standard.
Esempio n. 1
Calcola il limite $\lim_(x\to\infty)\left(\frac(3x+1)(3x-5)\right)^(4x+7)$.
Notiamo subito che la base del grado (cioè $\frac(3x+1)(3x-5)$) tende all'unità:
$$ \lim_(x\to\infty)\frac(3x+1)(3x-5)=\left|\frac(\infty)(\infty)\right| =\lim_(x\to\infty)\frac(3+\frac(1)(x))(3-\frac(5)(x)) =\frac(3+0)(3-0) = 1. $$
In questo caso l'esponente (espressione $4x+7$) tende all'infinito, cioè $\lim_(x\to\infty)(4x+7)=\infty$.
La base del grado tende all'unità, l'esponente tende all'infinito, cioè abbiamo a che fare con l'incertezza $1^\infty$. Applichiamo una formula per rivelare questa incertezza. Alla base della potenza della formula c'è l'espressione $1+\frac(1)(x)$, e nell'esempio che stiamo considerando la base della potenza è: $\frac(3x+1)(3x- 5)$. Pertanto, la prima azione sarà una modifica formale dell'espressione $\frac(3x+1)(3x-5)$ nella forma $1+\frac(1)(x)$. Innanzitutto, aggiungi e sottrai uno:
$$ \lim_(x\to\infty)\left(\frac(3x+1)(3x-5)\right)^(4x+7) =|1^\infty| =\lim_(x\to\infty)\sinistra(1+\frac(3x+1)(3x-5)-1\destra)^(4x+7) $$
Tieni presente che non puoi semplicemente aggiungere un'unità. Se siamo costretti ad aggiungerne uno, allora dobbiamo anche sottrarlo per non cambiare il valore dell'intera espressione. Per continuare la soluzione, ne teniamo conto
$$ \frac(3x+1)(3x-5)-1 =\frac(3x+1)(3x-5)-\frac(3x-5)(3x-5) =\frac(3x+1- 3x+5)(3x-5) =\frac(6)(3x-5). $$
Poiché $\frac(3x+1)(3x-5)-1=\frac(6)(3x-5)$, allora:
$$ \lim_(x\to\infty)\left(1+ \frac(3x+1)(3x-5)-1\right)^(4x+7) =\lim_(x\to\infty)\ sinistra(1+\frac(6)(3x-5)\destra)^(4x+7) $$
Continuiamo la regolazione. Nell'espressione $1+\frac(1)(x)$ della formula, il numeratore della frazione è 1, mentre nella nostra espressione $1+\frac(6)(3x-5)$ il numeratore è $6$. Per ottenere $ 1 $ al numeratore, inserisci $ 6 $ al denominatore utilizzando la seguente conversione:
$$ 1+\frac(6)(3x-5) =1+\frac(1)(\frac(3x-5)(6)) $$
Così,
$$ \lim_(x\to\infty)\left(1+\frac(6)(3x-5)\right)^(4x+7) =\lim_(x\to\infty)\left(1+ \frac(1)(\frac(3x-5)(6))\destra)^(4x+7) $$
Quindi, la base della laurea, ad es. $1+\frac(1)(\frac(3x-5)(6))$, adattato alla forma $1+\frac(1)(x)$ richiesta nella formula. Ora iniziamo a lavorare con l'esponente. Nota che nella formula le espressioni agli esponenti e al denominatore sono le stesse:
Ciò significa che nel nostro esempio l'esponente e il denominatore devono essere portati alla stessa forma. Per ottenere l'espressione $\frac(3x-5)(6)$ nell'esponente, moltiplichiamo semplicemente l'esponente per questa frazione. Naturalmente, per compensare tale moltiplicazione, dovrai moltiplicare immediatamente per la frazione reciproca, cioè per $\frac(6)(3x-5)$. Quindi abbiamo:
$$ \lim_(x\to\infty)\left(1+\frac(1)(\frac(3x-5)(6))\right)^(4x+7) =\lim_(x\to\ infty)\left(1+\frac(1)(\frac(3x-5)(6))\right)^(\frac(3x-5)(6)\cdot\frac(6)(3x-5 )\cdot(4x+7)) =\lim_(x\to\infty)\left(\left(1+\frac(1)(\frac(3x-5)(6))\right)^(\ frac(3x-5)(6))\destra)^(\frac(6\cdot(4x+7))(3x-5)) $$
Consideriamo separatamente il limite della frazione $\frac(6\cdot(4x+7))(3x-5)$ situato nella potenza:
$$ \lim_(x\to\infty)\frac(6\cdot(4x+7))(3x-5) =\left|\frac(\infty)(\infty)\right| =\lim_(x\to\infty)\frac(6\cdot\left(4+\frac(7)(x)\right))(3-\frac(5)(x)) =6\cdot\ frac(4)(3) =8. $$
Risposta: $\lim_(x\to(0))\biggl(\cos(2x)\biggr)^(\frac(1)(\sin^2(3x)))=e^(-\frac(2) (9))$.
Esempio n.4
Trova il limite $\lim_(x\to+\infty)x\left(\ln(x+1)-\ln(x)\right)$.
Poiché per $x>0$ abbiamo $\ln(x+1)-\ln(x)=\ln\left(\frac(x+1)(x)\right)$, allora:
$$ \lim_(x\to+\infty)x\left(\ln(x+1)-\ln(x)\right) =\lim_(x\to+\infty)\left(x\cdot\ln\ sinistra(\frac(x+1)(x)\destra)\destra) $$
Espandendo la frazione $\frac(x+1)(x)$ nella somma delle frazioni $\frac(x+1)(x)=1+\frac(1)(x)$ otteniamo:
$$ \lim_(x\to+\infty)\left(x\cdot\ln\left(\frac(x+1)(x)\right)\right) =\lim_(x\to+\infty)\left (x\cdot\ln\left(1+\frac(1)(x)\right)\right) =\lim_(x\to+\infty)\left(\ln\left(\frac(x+1) (x)\destra)^x\destra) =\ln(e) =1. $$
Risposta: $\lim_(x\to+\infty)x\left(\ln(x+1)-\ln(x)\right)=1$.
Esempio n.5
Trova il limite $\lim_(x\to(2))\biggl(3x-5\biggr)^(\frac(2x)(x^2-4))$.
Poiché $\lim_(x\to(2))(3x-5)=6-5=1$ e $\lim_(x\to(2))\frac(2x)(x^2-4)= \ infty$, allora abbiamo a che fare con un'incertezza della forma $1^\infty$. Spiegazioni dettagliate sono fornite nell'esempio n. 2, ma qui ci limiteremo ad una breve soluzione. Effettuando la sostituzione $t=x-2$, otteniamo:
$$ \lim_(x\to(2))\biggl(3x-5\biggr)^(\frac(2x)(x^2-4)) =\left|\begin(allineato)&t=x-2 ;\;x=t+2\\&t\to(0)\end(allineato)\right| =\lim_(t\to(0))\biggl(1+3t\biggr)^(\frac(2t+4)(t^2+4t))=\\ =\lim_(t\to(0) )\biggl(1+3t\biggr)^(\frac(1)(3t)\cdot 3t\cdot\frac(2t+4)(t^2+4t)) =\lim_(t\to(0) )\sinistra(\biggl(1+3t\biggr)^(\frac(1)(3t))\destra)^(\frac(6\cdot(t+2))(t+4)) =e^ 3. $$
Puoi risolvere questo esempio in un modo diverso, utilizzando la sostituzione: $t=\frac(1)(x-2)$. Ovviamente la risposta sarà la stessa:
$$ \lim_(x\to(2))\biggl(3x-5\biggr)^(\frac(2x)(x^2-4)) =\left|\begin(allineato)&t=\frac( 1)(x-2);\;x=\frac(2t+1)(t)\\&t\to\infty\end(aligned)\right| =\lim_(t\to\infty)\left(1+\frac(3)(t)\right)^(t\cdot\frac(4t+2)(4t+1))=\\ =\lim_ (t\to\infty)\left(1+\frac(1)(\frac(t)(3))\right)^(\frac(t)(3)\cdot\frac(3)(t) \cdot\frac(t\cdot(4t+2))(4t+1)) =\lim_(t\to\infty)\left(\left(1+\frac(1)(\frac(t)( 3))\right)^(\frac(t)(3))\right)^(\frac(6\cdot(2t+1))(4t+1)) =e^3. $$
Risposta: $\lim_(x\to(2))\biggl(3x-5\biggr)^(\frac(2x)(x^2-4))=e^3$.
Esempio n.6
Trova il limite $\lim_(x\to\infty)\left(\frac(2x^2+3)(2x^2-4)\right)^(3x) $.
Scopriamo a cosa tende l'espressione $\frac(2x^2+3)(2x^2-4)$ nella condizione $x\to\infty$:
$$ \lim_(x\to\infty)\frac(2x^2+3)(2x^2-4) =\sinistra|\frac(\infty)(\infty)\destra| =\lim_(x\to\infty)\frac(2+\frac(3)(x^2))(2-\frac(4)(x^2)) =\frac(2+0)(2 -0)=1. $$
In un dato limite abbiamo quindi a che fare con un'incertezza della forma $1^\infty$, che riveleremo utilizzando il secondo limite notevole:
$$ \lim_(x\to\infty)\left(\frac(2x^2+3)(2x^2-4)\right)^(3x) =|1^\infty| =\lim_(x\to\infty)\left(1+\frac(2x^2+3)(2x^2-4)-1\right)^(3x)=\\ =\lim_(x\to \infty)\left(1+\frac(7)(2x^2-4)\right)^(3x) =\lim_(x\to\infty)\left(1+\frac(1)(\frac (2x^2-4)(7))\destra)^(3x)=\\ =\lim_(x\to\infty)\sinistra(1+\frac(1)(\frac(2x^2-4 )(7))\destra)^(\frac(2x^2-4)(7)\cdot\frac(7)(2x^2-4)\cdot 3x) =\lim_(x\to\infty) \left(\left(1+\frac(1)(\frac(2x^2-4)(7))\right)^(\frac(2x^2-4)(7))\right)^( \frac(21x)(2x^2-4)) =e^0 =1. $$
Risposta: $\lim_(x\to\infty)\left(\frac(2x^2+3)(2x^2-4)\right)^(3x)=1$.
