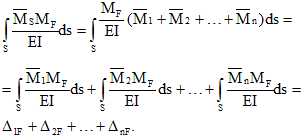Hitung sistem batang statis tak tentu datar. Perhitungan sistem statis tak tentu dengan metode gaya

Sistem statis tak tentu disebut sistem batang, untuk menentukan reaksi tumpuan di mana persamaan kesetimbangan saja tidak cukup. Dari sudut pandang kinematik, ini adalah sistem batang, jumlah derajat kebebasannya kurang dari jumlah ikatan. Untuk mengungkapkan ketidaktentuan statis sistem tersebut, perlu untuk menyusun persamaan kompatibilitas deformasi tambahan. Jumlah persamaan tersebut ditentukan oleh jumlah ketidakpastian statis dari sistem batang. Gambar 8.14 menunjukkan contoh balok dan rangka statis tak tentu.

Balok yang ditunjukkan pada Gambar 8.14b disebut kontinu balok. Nama ini berasal dari fakta bahwa dukungan perantara hanya mendukung balok. Pada titik tumpu, balok tidak dipotong oleh engsel, engsel tidak dipotong ke badan balok. Oleh karena itu, pengaruh tegangan dan deformasi yang dialami balok pada bentang kiri juga mempengaruhi bentang kanan. Jika engsel dipotong ke badan balok di tempat penopang perantara, maka sebagai hasilnya sistem akan menjadi statis tertentu - dari satu balok kita akan mendapatkan dua balok yang independen satu sama lain, yang masing-masing akan ditentukan secara statis . Perlu dicatat bahwa balok menerus kurang intensif material dibandingkan dengan balok split, karena balok tersebut lebih rasional mendistribusikan momen lentur sepanjang panjangnya. Dalam hal ini, balok kontinu banyak digunakan dalam konstruksi dan teknik. Namun, balok kontinu, karena statis tak tentu, memerlukan teknik perhitungan khusus, yang mencakup penggunaan deformasi sistem.

Sebelum melanjutkan ke perhitungan sistem statis tak tentu, perlu dipelajari cara menentukan tingkat ketidakpastian statisnya. Salah satu aturan paling sederhana untuk menentukan derajat ketidakpastian statis adalah sebagai berikut:

, (8.3)

di mana jumlah ikatan yang dikenakan pada struktur; jumlah kemungkinan persamaan kesetimbangan independen yang dapat dikompilasi untuk sistem yang dipertimbangkan.

Kami menggunakan persamaan (8.3) untuk menentukan derajat ketidaktentuan statis sistem yang ditunjukkan pada Gambar 8.14.

Balok yang ditunjukkan pada Gambar 8.14a pernah statis tak tentu, karena memiliki tiga ikatan pada kaki kiri dan satu ikatan pada kaki kanan. Hanya ada tiga persamaan kesetimbangan independen untuk balok seperti itu. Jadi, derajat ketidakpastian statik balok
. Balok menerus yang ditunjukkan pada Gambar 8.14b juga pernah statis tak tentu, karena memiliki dua sambungan pada penyangga kiri dan satu sambungan masing-masing pada penyangga tengah dan penyangga kanan - total empat sambungan. Jadi, derajat ketidaktentuan statisnya
.

Bingkai yang ditunjukkan pada gambar. 8.14c, adalah tiga kali statis tak tentu, karena memiliki enam ikatan pada penyangga. Hanya ada tiga persamaan keseimbangan independen untuk kerangka ini. Jadi, derajat ketidakpastian statik untuk kerangka ini dari persamaan (8.3) adalah:
. Derajat ketidakpastian statis dari bingkai yang ditunjukkan pada Gambar. 8.18, d sama dengan empat, karena bingkai memiliki tujuh koneksi pada penyangga. Oleh karena itu, derajat ketidaktentuan statisnya sama dengan
.

Aturan (8.3) untuk menentukan derajat ketidakpastian statis hanya digunakan untuk sistem sederhana. Dalam kasus yang lebih kompleks, aturan ini tidak berfungsi. Gambar 8.15 menunjukkan kerangka yang derajat ketidakpastian statisnya tidak dapat ditentukan dengan menggunakan Persamaan (8.3).

Secara eksternal, sistem yang ditunjukkan pada Gambar 8.15 adalah lima kali statis tak tentu. Ini mudah ditentukan dengan menggunakan persamaan (8.3): dari enam ikatan eksternal (tiga di bagian A, tiga di bagian B dan dua di bagian C), tiga persamaan kesetimbangan yang mungkin dikurangi. Namun, sistem ini juga memiliki ketidakpastian statis internal. Tidak mungkin untuk memperhitungkan ketidaktentuan statis internal menggunakan persamaan (8.3). Sebelum beralih ke penentuan derajat ketidaktentuan statis dari kerangka yang ditunjukkan pada Gambar 8.15, kami memperkenalkan beberapa definisi. Yang pertama dari definisi ini mencakup gagasan tentang engsel sederhana.

Sederhana disebut engsel yang menghubungkan dua batang (Gbr. 8.16).

Gbr.8.16. engsel sederhana

Engsel yang menghubungkan beberapa batang disebut sulit(Gbr.8.17).

Gbr.8.17. engsel kompleks

Jumlah engsel sederhana yang dapat menggantikan satu engsel kompleks ditentukan dari rumus:

, (8.4)

di mana
- jumlah batang yang termasuk dalam simpul.

Kami menghitung ulang engsel kompleks yang ditunjukkan pada Gambar 8.17 menjadi jumlah engsel sederhana menggunakan rumus (8.4):
. Dengan demikian, engsel kompleks yang ditunjukkan pada Gambar 8.17 dapat diganti dengan empat engsel sederhana.

Mari kita perkenalkan satu konsep lagi - lingkaran tertutup.

Mari kita buktikan teorema: setiap loop tertutup adalah tiga kali statis tak tentu.

Untuk membuktikan teorema, pertimbangkan sirkuit tertutup yang dibebani dengan gaya eksternal (Gbr.8.18).

Mari kita potong kontur tertutup dengan bagian vertikal dan tunjukkan faktor gaya internal yang muncul di lokasi bagian. Tiga faktor internal muncul di setiap bagian: gaya geser , momen lentur
dan gaya memanjang
. Secara total, masing-masing bagian kontur, selain gaya eksternal, dipengaruhi oleh enam faktor internal (Gbr. 8.18, b, c). Mempertimbangkan keseimbangan salah satu bagian cut-off, misalnya bagian kiri (Gbr. 8.18, b), kami menemukan bahwa masalahnya adalah tiga kali statis tak tentu, karena hanya tiga persamaan kesetimbangan independen yang dapat dikompilasi untuk pemotongan -off bagian, dan ada enam gaya yang tidak diketahui yang bekerja pada bagian cut-off. Dengan demikian, derajat ketidakpastian statis dari loop tertutup sama dengan
. Teorema telah terbukti.

Sekarang, dengan menggunakan konsep engsel sederhana dan loop tertutup, kita dapat merumuskan aturan lain untuk menentukan derajat ketidakpastian statis:

, (8.5)

di mana
jumlah loop tertutup;
jumlah engsel dalam hal yang sederhana (8.4).

Dengan menggunakan persamaan (8.5), kita menentukan derajat ketidaktentuan statis dari kerangka yang ditunjukkan pada Gambar 8.15. Bingkai memiliki lima kontur
, termasuk kontur yang dibentuk oleh batang penyangga. Engsel pada simpul D sederhana, karena menghubungkan dua batang. Engsel di bagian K rumit, karena menghubungkan empat batang. Banyaknya engsel sederhana yang dapat menggantikan engsel pada bagian K adalah, menurut rumus (8.4):
. Engsel C juga rumit karena menghubungkan tiga batang. Untuk engsel ini
. Selain itu, sistem ini memiliki dua engsel yang lebih sederhana, yang dengannya dipasang ke alas. Jadi, jumlah engsel sederhana dalam sistem adalah
. Mengganti jumlah loop tertutup
dan jumlah engsel sederhana
dalam rumus (8.5) kami menentukan tingkat ketidakpastian statis bingkai:
. Jadi, ditunjukkan pada Gambar. 8.15 bingkai, tujuh kali statis tak tentu. Dan ini berarti bahwa untuk menghitung sistem seperti itu, perlu untuk membuat, selain tiga persamaan kesetimbangan, tujuh persamaan kompatibilitas deformasi. Dengan memecahkan sistem 10 persamaan yang diperoleh dengan cara ini sehubungan dengan yang tidak diketahui yang termasuk dalam persamaan ini, dimungkinkan untuk menentukan besarnya reaksi dalam ikatan eksternal dan gaya internal yang timbul dalam kerangka. Prosedur untuk memecahkan masalah ini dapat disederhanakan dengan mengecualikan persamaan kesetimbangan dari sistem persamaan. Namun, pendekatan ini memerlukan penggunaan metode solusi khusus, salah satunya adalah metode gaya.

Sistem disebut statis tak tentu di mana gaya internal tidak dapat ditentukan hanya dari persamaan kesetimbangan (persamaan statis).

Konstruksi statis tak tentu memiliki apa yang disebut tak berguna koneksi. Mereka dapat terjadi pada penyangga, batang, dan elemen lainnya. Sambungan semacam itu disebut "berlebihan" karena tidak diperlukan untuk memastikan keseimbangan struktur, tetapi ditentukan oleh persyaratan kekuatan dan kekakuannya. Koneksi ekstra semacam itu disebut luar. Selain itu, koneksi yang tidak perlu dapat muncul karena fitur desain itu sendiri. Misalnya, kontur bingkai tertutup (Gbr. 46, G) memiliki tiga kekuatan internal yang tidak diketahui di setiap bagian, yaitu hanya enam, dan tiga di antaranya adalah "ekstra". Upaya ekstra ini disebut intern. Menurut jumlah koneksi "ekstra" eksternal atau internal, mereka membangun derajat ketidakpastian statis sistem. Ini sama dengan perbedaan antara jumlah yang tidak diketahui yang akan ditentukan dan jumlah persamaan statis. Dengan satu "ekstra" yang tidak diketahui, sistem disebut sekali, atau sekali statis tak tentu, dengan dua - dua kali tak tentu statis, dll.

Desain yang ditunjukkan pada gambar. 46, sebuah, pernah statis tak tentu, dan konstruksi yang ditunjukkan pada Gambar. 46, b dan di, - statis tak tentu ganda, pada Gambar. 46, d - tiga kali dengan konstruksi statis tak tentu.

Saat memecahkan masalah statis tak tentu, selain persamaan statis, persamaan digunakan yang memperhitungkan deformasi elemen struktural.

Ada beberapa metode untuk menyelesaikan masalah statis tak tentu: metode perbandingan perpindahan, metode gaya, metode perpindahan.

metode paksa

Saat menghitung sistem statis tak tentu, gaya dianggap tidak diketahui.

Perhitungan oleh metode paksa dilakukan dengan urutan sebagai berikut:

• 1. Tetapkan derajat ketidakpastian statis.
• 2. Dengan menghapus koneksi "ekstra", sistem asli diganti dengan yang statis tertentu, yang disebut sistem utama. Beberapa sistem tersebut dapat dibangun, sambil mengamati kondisi geo mereka

kekekalan metrik.

• 3. Sistem utama dimuat dengan kekuatan eksternal yang diberikan dan kekuatan "ekstra" yang tidak diketahui yang menggantikan aksi koneksi jarak jauh, yang mengakibatkan sistem yang setara.
• 4. Untuk memastikan ekivalensi sistem asal dan sistem utama, gaya yang tidak diketahui harus dipilih sehingga deformasi sistem utama tidak berbeda dari deformasi sistem statis tak tentu asli. Untuk tujuan ini, perpindahan titik-titik penerapan yang tidak diketahui "berlebihan" ke arah tindakannya disamakan dengan nol. Dari persamaan tambahan yang diperoleh dengan cara ini, nilai gaya "ekstra" yang tidak diketahui ditentukan. Menentukan perpindahan titik-titik yang sesuai dapat dilakukan dengan cara apa pun, tetapi lebih baik menggunakan metode Mohr yang paling umum.
• 5. Setelah menentukan nilai gaya "ekstra" yang tidak diketahui, reaksi ditentukan dan diagram gaya internal diplot, bagian dipilih dan kekuatan diperiksa dengan cara biasa.

Persamaan kanonik dari metode gaya

Persamaan perpindahan tambahan yang menyatakan persamaan dengan nol perpindahan dalam arah "ekstra" yang tidak diketahui dapat dengan mudah dikompilasi dalam apa yang disebut bentuk kanonik itu. menurut pola tertentu. Mari kita tunjukkan ini dengan contoh penyelesaian sistem statis tak tentu yang paling sederhana (Gbr. 47, sebuah).

Kami memilih konsol sebagai sistem utama, membuang dukungan yang diartikulasikan. Sistem ekuivalen akan diperoleh setelah penerapan gaya eksternal T 7 dan "ekstra" tidak diketahui X(Gbr. 47, b).

Persamaan Kanonik, yang menyatakan perpindahan titik nol PADA dari gaya F dan X, akan

Dari persamaan yang kita miliki

Untuk sistem yang memiliki dua koneksi "tambahan", sistem persamaan kanonik memiliki bentuk:

• 8 11 X 1 + b 12 ^2 + ^1
• 621-^1 + 622^2 "Aku" ^20-

Gerakan A[p Dan b [y, termasuk dalam persamaan kanonik, ditentukan dengan metode Mohr.

Untuk sistem yang terdiri dari elemen bujursangkar, akan lebih mudah untuk menghitung perpindahan menggunakan metode Vereshchagin.

Misalnya, untuk tugas yang digambarkan pada Gambar. 47, mengalikan diagram (Gbr. 48), kami memperoleh koefisien persamaan kanonik:

1 2 Saya 3 1 Saya / Saya 2 1 5 I1 3

E]L LL =-/ / -/ = -, E]A LR =-------- +-------.

1 11 2 3 3 1 1R 2 2 2 2 3 2/ 48 E]

Mendapatkan Kl - - = - E.

Mendefinisikan kekuatan X, kami benar-benar menemukan reaksi dukungan aku masuk. Selanjutnya, masalah penentuan faktor gaya internal dapat diselesaikan, seperti biasa, dengan menggunakan metode penampang.

KEMENTERIAN PENDIDIKAN FEDERASI RUSIA

LEMBAGA NEGARA

UNIVERSITAS TEKNIS NEGARA KUZBAS

Departemen Kekuatan Material

PERHITUNGAN SISTEM HINGE-ROD STATIS INDETERMINATE DI BAWAH TEGANGAN - KOMPRESI

Pedoman pelaksanaan tugas perhitungan dan grafik pada kekuatan materi untuk siswa semua spesialisasi

Disusun oleh: V.D. Moiseenko

Disetujui pada rapat departemen. Berita Acara No. 8 tanggal 29.06.01

Salinan elektronik ada di perpustakaan gedung utama KuzGTU

Kemerovo 2002

Pengantar. Ruang Lingkup dan Tujuan Penugasan

Sistem batang engsel statis tak tentu adalah sistem di mana gaya pada batang dan reaksi pada tumpuan tidak dapat ditentukan hanya dari kondisi kesetimbangan.

Gambar 1 menunjukkan braket konvensional yang terdiri dari dua batang. Gaya-gaya N1 dan N2 pada batang-batang braket ini dengan mudah ditentukan dari kondisi kesetimbangan untuk sistem gaya-gaya konvergen yang diterapkan pada titik potong C, karena dua persamaan untuk sistem gaya-gaya ini dengan dua yang tidak diketahui diselesaikan.

Jika desain braket rumit dengan menambahkan satu batang lagi (Gbr. 1, b), maka gaya pada batang tidak dapat ditentukan dengan cara yang sama, karena untuk simpul C, hanya dua persamaan keseimbangan statis yang masih dapat disusun (ΣХ = 0; Y = 0), dan jumlah gaya yang tidak diketahui adalah tiga. Kami pernah memiliki sistem statis tak tentu.

Dengan memperumit desain dan memperkenalkan batang baru, seseorang dapat memperoleh sistem statis tak tentu dua kali (lihat Gambar 1c), tiga kali, dan seterusnya. Oleh karena itu, di bawah n kali sistem statis tak tentu dipahami seperti sistem di mana jumlah koneksi melebihi jumlah persamaan statika independen oleh n unit.

Persamaan tambahan yang diperlukan untuk memecahkan masalah dapat ditemukan dengan mempertimbangkan sistem dalam keadaan terdeformasi dan membangun hubungan antara perpindahan dan deformasi elemen struktural. Persamaan yang dihasilkan disebut persamaan kompatibilitas regangan.

Gambar 2 menunjukkan diagram dari beberapa sistem statis tak tentu.

Gbr.2. Beberapa jenis sistem statis tak tentu

Saat mempelajari bagian "Sistem batang tak tentu statis" dan melakukan perhitungan dan tugas grafis ini, siswa harus mempelajari fitur sistem statis tak tentu; memperoleh keterampilan dalam pengungkapan ketidaktentuan statis, dalam menentukan gaya dalam elemen struktur dan memilih luas penampang dari kondisi kekuatan.

Tugas mengharuskan siswa untuk melakukan hal berikut:

- tentukan gaya pada batang dan pilih luas penampang dari aksi beban eksternal;

- tentukan tegangan tambahan pada batang karena perubahan suhu;

- menentukan tegangan pemasangan tambahan yang disebabkan oleh ketidaktepatan dalam pembuatan batang;

- pilih bagian batang sesuai dengan keadaan batas.

Volume dan bentuk pelaksanaan tugas perhitungan dan grafik tergantung pada volume kursus yang dipelajari dan dinegosiasikan oleh guru di kelas praktis.

1. Informasi teoretis singkat

Ketika memecahkan masalah statis tak tentu, urutan berikut harus diikuti:

1.1. Pertimbangkan sisi statis dari masalah. Buat rencana gaya dan tulis persamaan statika.

1.2. Pertimbangkan sisi geometris dari masalah. Buat rencana perjalanan. Kompilasi persamaan kompatibilitas deformasi tambahan sedemikian rupa sehingga semua gaya yang tidak diketahui dapat ditemukan.

1.3. Pertimbangkan sisi fisik masalahnya. Menurut hukum fisika (dengan perhitungan suhu) dan menurut hukum Hooke, nyatakan deformasi dalam persamaan kompatibilitasnya melalui gaya yang tidak diketahui yang bekerja pada batang:

1.4. Menghasilkan solusi gabungan dari persamaan statika, geometri, fisika dan menentukan gaya yang tidak diketahui.

1.5. Menggunakan kondisi kekuatan tekan atau tarik N/F = [ ], pilih luas penampang batang.

1.6. Dengan gaya yang diketahui pada batang dan luas penampang yang diterima, hitung tegangan normal menggunakan rumus

= N F .

2. Contoh

Diketahui: Balok AB yang benar-benar kaku diam, seperti ditunjukkan pada Gambar. 3, dibebani dengan beban dan gaya yang terdistribusi merata P.

Gbr.3. Diagram sistem statis tak tentu

Data awal untuk perhitungan

4. Tentukan tegangan total dalam batang dari aksi beban, perubahan suhu dan ketidakakuratan manufaktur.

2.1. Perhitungan sistem batang berengsel statis tak tentu untuk pemuatan eksternal

P = 30 kN q = 15 kN/m

A C B

Gbr.4. Skema desain awal

2.1.1. Sisi statis dari masalah

Sisi statis dari masalah dipertimbangkan oleh rencana kekuatan. Rencana gaya adalah skema desain yang menunjukkan semua gaya (baik yang diketahui maupun tidak diketahui) yang diterapkan pada elemen sistem batang berengsel, yang keseimbangannya dipertimbangkan (dalam kasus kami, ini adalah balok kaku AB). Mari kita potong batang baja dan tembaga dan mengganti bagian bawah yang dibuang dengan gaya internal (Gbr. 5).

P = 30 kN q = 15 kN/m

A C B

60 °

Beras. 5. Rencana gaya dari beban eksternal

Dari rencana gaya (lihat Gambar 5) kita tuliskan persamaan keseimbangan statis. Untuk menjawab pertanyaan pertama dari masalah, perlu diketahui gaya pada batang - baja dan tembaga. Tidak perlu menghitung reaksi penyangga berengsel dalam kasus ini. Jadi dari tiga

kemungkinan persamaan statika (ΣX = 0; Y = 0 ; m c = 0 ) kita tulis

salah satu yang tidak termasuk reaksi dari tumpuan tetap pivot C:

mC = 0

N CT a + q a 2 2 + p a + NM sin60o b = 0,

N ST 2 + 15 2 2 2 + 30 2 NM 0,866 4 = 0,

Setelah operasi aljabar, persamaan kesetimbangan akan berbentuk

2.1.2. Sisi geometris dari masalah

Sisi geometris dari masalah dipertimbangkan oleh rencana perpindahan. Rencana perpindahan adalah diagram desain yang menunjukkan posisi sistem batang berengsel sebelum dan sesudah pembebanan. Pada rencana perpindahan, kami menunjukkan perpindahan titik-titik balok (AA1 dan BB1),

deformasi absolut dari batang tembaga dan baja (∆ l ST ; l M )

(Gbr. 6). Selain itu, karena deformasi kecil, kami memindahkan titik-titik balok secara vertikal ke atas atau ke bawah, dan menandai deformasi batang miring dengan tegak lurus.

Beras. 6. Rencana perpindahan dari aksi beban eksternal

Menurut rencana perpindahan, kami menyusun persamaan untuk kompatibilitas deformasi. Pertama-tama, kami menulis rasio perpindahan titik-titik balok dari kesamaan segitiga AA1 C dan CBB1 (Gbr. 6):

Perpindahan titik balok (AA1 dan BB1) dinyatakan dalam deformasi

Ekspresi (2.3) dan (2.4) disubstitusikan ke dalam relasi (2.2):

2.1.3. Sisi fisik dari masalah

Persamaan kompatibilitas deformasi yang dihasilkan (2.5) dalam bentuk ini tidak dapat diselesaikan dengan persamaan kesetimbangan (2.1), karena jumlah yang tidak diketahui yang termasuk di dalamnya memiliki sifat yang berbeda.

Deformasi absolut l CT dan l M dalam persamaan (2.5) kami nyatakan

Kami telah memperoleh persamaan kompatibilitas regangan yang ditulis dalam bentuk gaya di batang.

2.1.4. Perpaduan

Mari kita bersama-sama menyelesaikan persamaan kesetimbangan (2.1) dan persamaan kompatibilitas deformasi (2.6).

NCT + 1,73NM = 45

0.67NCT \u003d 0.95NM.

Dari persamaan kedua sistem, kami menyatakan gaya N ST:

dan substitusikan ke persamaan pertama sistem.

Hasil positif dari N ST dan N M menegaskan asumsi kita tentang kompresi batang baja dan tegangan batang tembaga, yang berarti bahwa gaya pada batang adalah:

2.1.5. Pemilihan penampang batang

Pemilihan penampang batang dilakukan sesuai dengan kondisi kekuatan tarik - kompresi:

N F [σ] .

a) Luas penampang batang baja yang dibutuhkan dari kondisi kekuatan akan ditentukan:

b) Luas penampang batang tembaga yang dibutuhkan dari kondisi kekuatan akan ditentukan:

Dalam hal ini, sesuai dengan rasio luas yang diberikan, luas batang baja harus sama dengan:

FCT = 4 3 FM = 4 3 1,7 10- 4 = 1,275 10- 4 m2 ..

Kami menerima luas penampang batang yang besar:

Dengan luas penampang batang tembaga dan baja yang diterima, kami menentukan tegangan pada batang ini.

2.2. Perhitungan suhu sistem batang engsel statis tak tentu

Tujuan dari perhitungan suhu adalah untuk menentukan tegangan tambahan pada batang tembaga dan baja akibat perubahan suhu.

Misalkan sistem dipanaskan oleh t = 20 o C . Algoritma solusi tetap sama. Skema desain awal ditunjukkan pada gambar. 7.

Sistem batang di mana reaksi pendukung dan faktor gaya internal tidak dapat ditemukan hanya dari persamaan kesetimbangan disebut statis tak tentu.

Perbedaan antara jumlah gaya yang tidak diketahui yang diperlukan dan persamaan keseimbangan independen menentukan: derajat ketidakpastian statis sistem. Tingkat ketidaktentuan statis selalu sama dengan jumlah koneksi berlebihan (berlebihan), penghapusan yang mengubah sistem statis tak tentu menjadi sistem statis ditentukan geometris variabel. Baik koneksi eksternal (referensi) dan internal, yang memberlakukan batasan tertentu pada pergerakan bagian sistem relatif satu sama lain, dapat menjadi berlebihan.

Geometris tidak berubah-ubah sistem seperti itu disebut, perubahan bentuk yang hanya mungkin terjadi sehubungan dengan deformasi elemen-elemennya.

Variabel geometris sistem seperti itu disebut, elemen-elemen yang dapat bergerak di bawah aksi kekuatan eksternal tanpa deformasi (mekanisme).

Ditampilkan pada gambar. 12.1 bingkai memiliki tujuh tautan eksternal (dukungan). Untuk menentukan gaya-gaya dalam ikatan ini (reaksi pendukung), kita hanya dapat menyusun tiga persamaan kesetimbangan independen. Oleh karena itu, sistem ini memiliki empat koneksi redundan, yang berarti empat kali statis tak tentu. Jadi, derajat ketidakpastian statik untuk rangka datar adalah:

di mana R- jumlah reaksi dukungan.

Kontur yang terdiri dari sejumlah elemen (lurus atau lengkung) secara kaku (tanpa engsel) yang saling terhubung dan membentuk sirkuit tertutup disebut sirkuit tertutup. . Bingkai persegi panjang yang ditunjukkan pada Gambar 12.2 adalah loop tertutup. Ini adalah tiga kali statis tak tentu, karena untuk membuatnya statis tak tentu perlu untuk memotong salah satu elemen dan menghilangkan tiga koneksi tambahan. Reaksi dari ikatan ini adalah: gaya longitudinal, gaya transversal dan momen lentur yang bekerja pada tempat pemotongan; mereka tidak dapat ditentukan dengan menggunakan persamaan statika. Dalam kondisi serupa, dalam arti ketidakpastian statis, ada loop tertutup, yang selalu tiga kali statis tak tentu.

Pencantuman engsel dalam simpul bingkai di mana dua batang bertemu, atau menempatkannya di sembarang tempat pada sumbu batang, menghilangkan satu sambungan dan mengurangi tingkat ketidaktentuan statis keseluruhan sebanyak satu. Engsel seperti itu disebut tunggal atau sederhana (Gbr. 12.3).

Secara umum, setiap engsel termasuk dalam simpul penghubung c batang, mengurangi tingkat ketidakpastian statis dengan c-1 , karena engsel seperti itu menggantikan c-1 engsel tunggal (Gbr. 12.3). Dengan demikian, tingkat ketidakpastian statis sistem dengan adanya loop tertutup ditentukan oleh rumus.

Sistem seperti itu disebut statis tak tentu jika tidak dapat dihitung menggunakan persamaan statika saja, karena memiliki koneksi yang tidak perlu. Untuk menghitung sistem seperti itu, persamaan tambahan dikompilasi yang memperhitungkan deformasi sistem.

Sistem statis tak tentu memiliki beberapa ciri khas:

1. statis tak tentu struktur lebih kaku daripada yang sesuai ditentukan secara statis, karena mereka memiliki koneksi tambahan.
2. Dalam statis tak tentu sistem, ada kekuatan internal yang lebih kecil, yang menentukan efisiensinya dibandingkan dengan ditentukan secara statis sistem di bawah beban eksternal yang sama.
3. Pelanggaran koneksi yang tidak perlu di statis tak tentu sistem tidak selalu mengarah pada kehancuran, sedangkan hilangnya komunikasi dalam ditentukan secara statis sistem membuatnya geometris variabel.
4. Untuk perhitungan statis tak tentu sistem, perlu terlebih dahulu menentukan karakteristik geometris dari penampang elemen, mis. sebenarnya, bentuk dan ukurannya, karena perubahannya mengarah pada perubahan kekuatan dalam koneksi dan distribusi upaya baru di semua elemen sistem.
5. Saat menghitung statis tak tentu sistem, perlu untuk memilih bahan konstruksi terlebih dahulu, karena perlu mengetahui modulus elastisitasnya.
6. Dalam statis tak tentu sistem, efek suhu, penyelesaian dukungan, ketidakakuratan dalam pembuatan dan pemasangan menyebabkan upaya tambahan.

Utama metode perhitunganstatis tak tentu sistem adalah:

1. metode paksa. Di sini, gaya dianggap sebagai yang tidak diketahui - gaya dan momen.
2.Metode gerakan. Tidak diketahui faktor deformasi - sudut rotasi dan perpindahan linier.
3.metode campuran. Di sini, bagian dari yang tidak diketahui mewakili upaya, dan bagian lainnya mewakili perpindahan.
4. Metode gabungan. Ini digunakan dalam perhitungan sistem simetris untuk beban asimetris. Ternyata disarankan untuk menghitung sistem untuk komponen simetris dari beban yang diberikan dengan metode perpindahan, dan untuk komponen simetris terbalik - dengan metode gaya.
Selain metode analitik yang ditunjukkan, berbagai metode numerik digunakan dalam perhitungan sistem yang sangat kompleks.

Persamaan kanonik dari metode gaya

Untuk mendapatkan persamaan tambahan, yang disebutkan dalam paragraf sebelumnya, pertama-tama Anda harus memutar yang diberikan, n kali statis tak tentu sistem menjadi statis tertentu dengan menghapus koneksi yang tidak perlu dari itu. Sistem determinan statis yang dihasilkan disebut dasar. Perhatikan bahwa transformasi sistem yang diberikan menjadi sistem yang ditentukan secara statis tidak wajib. Kadang-kadang modifikasi metode gaya digunakan di mana sistem yang mendasarinya dapat statis tak tentu, namun, penyajian masalah ini berada di luar cakupan manual ini. Penghapusan ikatan apa pun tidak mengubah gaya internal dan deformasi sistem jika gaya dan momen tambahan diterapkan padanya, yang merupakan reaksi dari ikatan yang dibuang. Ini berarti bahwa jika beban tertentu dan reaksi tautan jarak jauh diterapkan ke sistem utama, maka sistem utama dan sistem yang diberikan akan menjadi setara.

Dalam sistem tertentu, tidak boleh ada perpindahan sepanjang arah tautan kaku yang ada, termasuk tautan yang dibuang selama transisi ke sistem utama, oleh karena itu, dalam sistem utama, perpindahan sepanjang arah tautan yang dibuang harus menjadi sama dengan nol. Dan untuk ini, reaksi ikatan yang dijatuhkan harus memiliki nilai yang ditentukan secara ketat.

Kondisi persamaan dengan nol perpindahan ke arah koneksi ke-i dari n yang dibuang berdasarkan prinsip independensi aksi gaya memiliki bentuk:

di mana indeks pertama menunjukkan arah pergerakan dan jumlah sambungan yang terputus, dan indeks kedua menunjukkan alasan yang menyebabkan pergerakan, yaitu. adalah gerakan searah ikatan ke-i, yang disebabkan oleh reaksi ikatan ke-k; - gerakan ke arah koneksi ke-i, yang disebabkan oleh aksi simultan dari seluruh beban eksternal.

Dalam metode gaya, reaksi ikatan ke-k biasanya dilambangkan dengan Xk. Mempertimbangkan penunjukan ini dan karena validitas hukum Hooke, perpindahan dapat direpresentasikan sebagai:

di mana adalah gerakan tunggal (atau spesifik) dalam arah ikatan ke-i, yang disebabkan oleh reaksi yaitu reaksi searah dengan Xk, tetapi sama dengan satu.

Substitusikan (2) ke (1), kita peroleh:

arti fisik persamaan (3): pergerakan dalam sistem utama ke arah sambungan ke-i yang dibuang sama dengan nol.

Menulis ekspresi yang mirip dengan (3) untuk seluruh rangkaian ikatan yang dibuang, kita peroleh sistem persamaan kanonikmetode paksa:

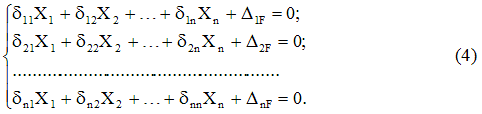
Bentuk persamaan (4), yaitu jumlah istilah di masing-masingnya dan jumlah totalnya hanya ditentukan oleh tingkat ketidakpastian statis sistem dan tidak bergantung pada fitur spesifiknya.

Koefisien sistem persamaan kanonik (4) ditentukan dengan metode Mohr-Vereshchagin dengan mengalikan diagram yang sesuai. Semua koefisien ini, sebagaimana dinyatakan di atas, mewakili perpindahan; koefisien yang berdiri di yang tidak diketahui adalah perpindahan satuan, dan anggota bebasnya adalah muatan. Gerakan tunggal dibagi menjadi utama, terletak di sepanjang diagonal utama dan memiliki indeks yang sama dan efek samping(). Gerakan besar selalu positif, tidak seperti gerakan sampingan. Perpindahan yang terletak secara simetris, sesuai dengan teorema tentang timbal balik perpindahan, adalah sama satu sama lain, yaitu. .

Algoritma untuk menghitung metode gaya

Terlepas dari fitur desain yang dipertimbangkan, urutan perhitungan sistem statis tak tentu berikut ini dapat dibedakan: metode paksa:

1. Tentukan tingkat ketidakpastian statis.
2. Pilih sistem utama.
3. Bentuk sistem yang setara.
4. Bakar sistemnya persamaan kanonik.
5. Buat diagram unit dan beban faktor gaya internal yang timbul pada elemen struktur yang dipertimbangkan.
6. Hitung koefisien dari yang tidak diketahui dan suku bebas dari sistem persamaan kanonik.
7. Buat diagram tunggal total.
8. Lakukan pemeriksaan universal dari koefisien untuk suku yang tidak diketahui dan suku bebas.
9. Selesaikan sistem (4), mis. menentukan reaksi ikatan ekstra.
10. Buat diagram faktor gaya internal yang muncul untuk sistem tertentu (dengan kata lain, diagram akhir).
11. Lakukan pemeriksaan statis dan kinematik.
Perhatikan bahwa poin 7, 8, 11 dari algoritma di atas tidak mutlak diperlukan, meskipun mereka memungkinkan Anda untuk mengontrol kebenaran perhitungan. Dan untuk sistem dengan satu koneksi tambahan, poin 7 dan 8 sama sekali tidak berarti, karena dalam hal ini total diagram tunggal bertepatan dengan yang tunggal.
Mari kita lihat lebih dekat beberapa langkah perhitungan di atas.

Memilih Sistem Utama

Ini adalah tahap perhitungan yang paling penting, karena pilihan rasional dari sistem utama sangat menyederhanakan pekerjaan komputasi. Mari kita pertimbangkan kemungkinan cara untuk menghapus koneksi yang tidak perlu, yang menentukan bentuk sistem utama.

1. Penolakan koneksi yang tidak perlu dilakukan dengan penghapusan total beberapa dukungan atau penggantiannya dengan dukungan dengan jumlah koneksi yang lebih kecil. Reaksi yang bekerja dalam arah ikatan yang dijatuhkan adalah redundan yang tidak diketahui. Gambar 1, b, c, d menunjukkan berbagai versi sistem ekivalen yang diperoleh dengan metode ini untuk kerangka (Gbr. 1, a).

2. Penempatan engsel di bagian tengah batang memungkinkan di setiap bagian tersebut untuk membuat sambungan yang sesuai dengan momen lentur. Momen-momen ini tidak diketahui secara berlebihan. Untuk bingkai dengan tingkat ketidakpastian statis n = 3 (Gbr. 2, a), ketika memilih sistem utama, tiga engsel harus dipasang. Posisi engsel ini dapat berubah-ubah, tetapi memenuhi persyaratan invariabilitas geometrik sistem (Gbr. 2b).

3. Diseksi batang menghilangkan tiga ikatan yang sesuai dengan gaya internal M, Q, N (Gbr. 2, c). Dalam kasus tertentu (Gbr. 2d), memotong batang sepanjang engsel melepaskan dua ikatan (Gbr. 2, e), dan memotong batang lurus dengan engsel di ujungnya melepaskan satu ikatan (Gbr. 2, f).

Di antara koneksi dari sistem statis tak tentu, mutlak diperlukan dan kondisional diperlukan dibedakan. Yang mutlak diperlukan adalah tautan, setelah dihilangkan, sistem menjadi dapat diubah secara geometris. Koneksi yang mutlak diperlukan dicirikan oleh determinabilitas statis dari upaya di dalamnya, mis. reaksi ikatan semacam itu dapat dihitung dari kondisi kesetimbangan. Saat memilih sistem utama, koneksi yang benar-benar diperlukan tidak dapat dibuang.

Hubungan, setelah dihilangkan, di mana sistem terus tetap tidak berubah secara geometris, disebut perlu bersyarat. Sistem yang telah dibatalkan tautannya mungkin merupakan sistem utama metode paksa.

Perhitungan koefisien dan suku bebas persamaan kanonik

Tahap perhitungan ini didahului dengan konstruksi unit dan diagram beban faktor gaya internal (untuk balok dan rangka - diagram momen lentur). Diagram satuan dibangun dari aksi gaya satuan tak berdimensi atau momen satuan tak berdimensi, yang searah dengan arah kelebihan terkait yang tidak diketahui dalam sistem ekivalen, dan dilambangkan dengan , dan diagram satuan - oleh .

Diagram beban dibangun dari beban eksternal yang diterapkan pada sistem utama. Dalam hal ini, Anda dapat membuat satu diagram dari aksi simultan semua beban eksternal atau beberapa diagram, secara terpisah dari masing-masing beban yang diterapkan. Pembagian satu diagram beban menjadi beberapa yang lebih sederhana, sebagai suatu peraturan, disarankan hanya jika di antara beban yang ada ada beban yang terdistribusi secara merata, dan diagram momen di bagian yang sesuai di bawahnya adalah tanda bolak-balik. Dalam hal ini, dalam setiap persamaan kanonik, jumlah suku bebas akan sama dengan jumlah diagram beban yang diplot.

Perpindahan satuan dan beban (koefisien dan suku bebas persamaan kanonik) umumnya dapat dihitung dengan metode Mohr. Untuk balok dan bingkai, ini dapat dilakukan dengan menggunakan aturan Vereshchagin.

Verifikasi universal koefisien dan suku bebas persamaan kanonik

Untuk melakukan pemeriksaan universal, perlu untuk membuat diagram unit total - diagram momen dari aksi simultan semua unit gaya yang diterapkan pada sistem utama:

Kami mengalikan total diagram tunggal dengan diagram:

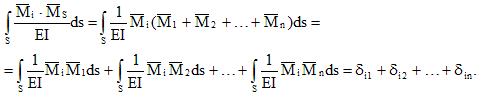
Dengan demikian, hasil perkalian total dan diagram tunggal ke-i adalah gerakan ke arah koneksi ke-i dari aksi gabungan dari satu ekstra yang tidak diketahui. Perpindahan ini sama dengan jumlah koefisien persamaan kanonik ke-i:

Pemeriksaan ini disebut baris demi baris dan berlaku untuk setiap persamaan kanonik.
Alih-alih n pemeriksaan baris, yang paling sering dilakukan - pemeriksaan universal, yang terdiri dari mengalikan diagram unit total dengan dirinya sendiri dan memeriksa kondisinya:

Jika pemeriksaan universal dilakukan, maka perpindahan unit dihitung dengan benar; jika tidak, perlu untuk melakukan pemeriksaan baris demi baris, yang akan memungkinkan Anda untuk mengklarifikasi perpindahan, selama perhitungan yang membuat kesalahan.

Untuk memeriksa perpindahan beban, perlu untuk mengalikan unit total dan diagram beban momen lentur:

Dengan demikian, verifikasi persyaratan bebas dari sistem persamaan kanonik (4) terdiri dari pemenuhan kondisi.