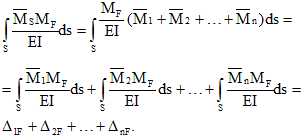Izračunajte ravan statički neodređen sistem štapova. Proračun statički neodređenih sistema metodom sila

Statički neodređeni sistemi nazivaju se štapni sistemi, za određivanje reakcija nosača u kojima samo jednadžbe ravnoteže nisu dovoljne. Sa kinematičke tačke gledišta, to su takvi sistemi šipki, čiji je broj stupnjeva slobode manji od broja veza. Da bi se otkrila statička neodređenost takvih sistema, potrebno je sastaviti dodatne jednadžbe kompatibilnosti deformacija. Broj takvih jednačina određen je brojem statičke neodređenosti štapnog sistema. Slika 8.14 prikazuje primjere statički neodređenih greda i okvira.

Greda prikazana na slici 8.14b se zove kontinuirano greda. Ovaj naziv dolazi od činjenice da srednji oslonac podržava samo gredu. Na mjestu oslonca, greda nije sječena šarkom, šarka nije urezana u tijelo grede. Dakle, utjecaj naprezanja i deformacija koje greda doživljava na lijevom rasponu utječe i na desni raspon. Ako se šarka usiječe u tijelo grede na mjestu srednjeg oslonca, tada će sistem postati statički određen - od jedne grede ćemo dobiti dvije grede neovisne jedna o drugoj, od kojih će svaka biti statički određena . Treba napomenuti da su kontinuirane grede manje materijalno intenzivne u odnosu na podijeljene grede, jer racionalnije raspoređuju momente savijanja duž svoje dužine. U tom smislu, kontinuirane grede se široko koriste u građevinarstvu i inženjerstvu. Međutim, kontinuirane grede, budući da su statički neodređene, zahtijevaju posebnu tehniku ​​proračuna, koja uključuje korištenje deformacija sistema.

Prije nego što pređemo na proračun statički neodređenih sistema, potrebno je naučiti kako odrediti stepen njihove statičke neodređenosti. Jedno od najjednostavnijih pravila za određivanje stepena statičke neodređenosti je sljedeće:

, (8.3)

gdje  broj veza nametnutih na konstrukciju;  broj mogućih nezavisnih jednačina ravnoteže koje se mogu sastaviti za sistem koji se razmatra.

Koristimo jednačinu (8.3) da odredimo stepen statičke neodređenosti sistema prikazanih na slici 8.14.

Greda prikazana na slici 8.14a je jednom statički neodređena, jer ima tri veze na lijevoj nozi i jednu vezu na desnoj nozi. Postoje samo tri nezavisne jednadžbe ravnoteže za takav snop. Dakle, stepen statičke neodređenosti snopa
. Kontinuirana greda prikazana na slici 8.14b je također jednom statički neodređena, jer ima dvije veze na lijevom nosaču i po jednu vezu na srednjem nosaču i na desnom nosaču - ukupno četiri veze. Dakle, stepen njegove statičke neodređenosti
.

Okvir prikazan na sl. 8.14c, tri puta je statički neodređen, jer ima šest veza u nosačima. Postoje samo tri nezavisne jednačine ravnoteže za ovaj okvir. Dakle, stepen statičke nesigurnosti za ovaj okvir iz jednačine (8.3) je:
. Stupanj statičke neodređenosti okvira prikazanog na slici 8.18, d je jednak četiri, budući da okvir ima sedam veza na nosačima. Dakle, stepen njegove statičke neodređenosti je jednak
.

Pravilo (8.3) za određivanje stepena statičke neodređenosti koristi se samo za jednostavne sisteme. U složenijim slučajevima ovo pravilo ne funkcionira. Slika 8.15 prikazuje okvir čiji se stepen statičke nesigurnosti ne može odrediti pomoću jednačine (8.3).

Spolja, sistem prikazan na slici 8.15 je pet puta statički neodređen. Ovo je lako uspostaviti pomoću jednačine (8.3): od šest vanjskih veza (tri u dijelu A, tri u dijelu B i dvije u dijelu C) oduzimaju se tri moguće jednačine ravnoteže. Međutim, ovaj sistem ima i unutrašnju statičku neodređenost. Nemoguće je uzeti u obzir unutrašnju statičku neodređenost pomoću jednačine (8.3). Pre nego što pređemo na određivanje stepena statičke neodređenosti okvira prikazanog na slici 8.15, uvodimo nekoliko definicija. Prva od ovih definicija uključuje pojam jednostavne šarke.

Jednostavno naziva se šarka koja spaja dvije šipke (slika 8.16).

Sl.8.16. jednostavna šarka

Šarka koja spaja nekoliko šipki naziva se teško(Sl.8.17).

Sl.8.17. složena šarka

Broj jednostavnih šarki koje mogu zamijeniti jednu složenu šarku određuje se iz formule:

, (8.4)

gdje
- broj šipki uključenih u čvor.

Preračunavamo složenu šarku prikazanu na slici 8.17 u broj jednostavnih šarki koristeći formulu (8.4):
. Dakle, složena šarka prikazana na slici 8.17 može se zamijeniti sa četiri jednostavne šarke.

Hajde da predstavimo još jedan koncept - zatvorena petlja.

Dokažimo teoremu: svaka zatvorena petlja je tri puta statički neodređena.

Da bismo dokazali teoremu, razmotrimo zatvoreno kolo opterećeno vanjskim silama (slika 8.18).

Izrežemo zatvorenu konturu vertikalnim presjekom i pokažemo unutrašnje faktore sile koji nastaju na mjestu presjeka. Tri interna faktora se javljaju u svakom od sekcija: sila smicanja , moment savijanja
i uzdužna sila
. Ukupno, na svaki odsječeni dio konture, osim vanjskih sila, djeluje i šest unutrašnjih faktora (sl. 8.18, b, c). Uzimajući u obzir ravnotežu jednog od odsječenih dijelova, na primjer, lijevog (slika 8.18, b), saznajemo da je problem tri puta statički neodređen, jer se za rez mogu kompilirati samo tri nezavisne jednadžbe ravnoteže. -odsječeni dio, a na odsječeni dio djeluje šest nepoznatih sila. Dakle, stepen statičke neodređenosti zatvorene petlje je jednak
. Teorema je dokazana.

Sada, koristeći koncept jednostavne šarke i zatvorene petlje, možemo formulirati još jedno pravilo za određivanje stupnja statičke neodređenosti:

, (8.5)

gdje
 broj zatvorenih petlji;
 broj šarki u smislu prostih (8.4).

Pomoću jednačine (8.5) određujemo stepen statičke neodređenosti okvira prikazanog na slici 8.15. Okvir ima pet kontura
, uključujući konturu koju čine potporne šipke. Šarka na čvoru D je jednostavna, jer povezuje dvije šipke. Šarka u sekciji K je složena, jer povezuje četiri šipke. Broj jednostavnih šarki koje bi mogle zamijeniti šarku u sekciji K je, prema formuli (8.4):
. Šarka C je takođe složena jer povezuje tri šipke. Za ovu šarku
. Osim toga, sistem ima još dvije jednostavne šarke, pomoću kojih je pričvršćen za bazu. Dakle, broj jednostavnih šarki u sistemu je
. Zamjena broja zatvorenih petlji
i broj jednostavnih šarki
u formuli (8.5) određujemo stepen statičke neodređenosti okvira:
. Dakle, prikazano na sl. 8.15 okvir, sedam puta statički neodređen. A to znači da je za proračun takvog sistema potrebno, pored tri jednačine ravnoteže, sastaviti i sedam jednačina kompatibilnosti deformacija. Rešavanjem ovako dobijenog sistema od 10 jednačina u odnosu na nepoznanice koje su uključene u ove jednačine, moguće je odrediti i veličinu reakcija u spoljašnjim vezama i unutrašnje sile koje nastaju u okviru. Procedura za rješavanje ovog problema može se donekle pojednostaviti isključivanjem jednačina ravnoteže iz sistema jednačina. Međutim, ovaj pristup zahtijeva korištenje posebnih metoda rješenja, od kojih je jedna metoda sile.

Sistemi se nazivaju statički neodređeni u kojima se unutrašnje sile ne mogu odrediti samo iz jednačina ravnoteže (statičke jednačine).

Statički neodređene konstrukcije imaju tzv suvišno veze. Mogu se pojaviti u nosačima, šipkama i drugim elementima. Takvi spojevi nazivaju se "suvišnim" jer nisu potrebni da bi se osigurala ravnoteža konstrukcije, već su određeni zahtjevima za njenu čvrstoću i krutost. Takve dodatne veze se nazivaju vanjski. Osim toga, mogu se pojaviti nepotrebne veze zbog karakteristika samog dizajna. Na primjer, zatvorena kontura okvira (Sl. 46, G) ima tri nepoznate unutrašnje sile u svakom preseku, tj. samo šest, a tri su "ekstra". Ovaj dodatni napor se zove interni. Prema broju eksternih ili unutrašnjih "ekstra" veza uspostavljaju stepen statičke neodređenosti sistema. Jednaka je razlici između broja nepoznatih koje treba odrediti i broja statičkih jednačina. Sa jednom "ekstra" nepoznatom, sistem se naziva jednom, ili jednom statički neodređenim, sa dve - dvaput statički neodređenim, itd.

Dizajn prikazan na sl. 46, a, jednom je statički neodređena, a konstrukcije prikazane na sl. 46, b i u, - dvostruko statički neodređeno, na sl. 46, d - tri puta sa statički neodređenim konstruktom.

Prilikom rješavanja statički neodređenih zadataka, pored statičkih jednadžbi, koriste se i jednadžbe koje uzimaju u obzir deformacije konstrukcijskih elemenata.

Postoji nekoliko metoda za rješavanje statički neodređenih problema: metoda poređenja pomaka, metoda sila, metoda pomaka.

metoda sile

Pri proračunu statički neodređenih sistema, sile se uzimaju kao nepoznanice.

Obračun po metoda sile izvodi se u sljedećem redoslijedu:

• 1. Postavite stepen statičke nesigurnosti.
• 2. Uklanjanjem "dodatnih" veza, originalni sistem se zamjenjuje statički određenim, tzv. glavni sistem. Može se izgraditi nekoliko takvih sistema, uz praćenje stanja njihovog geografskog položaja

metrička nepromjenjivost.

• 3. Glavni sistem je opterećen datim vanjskim silama i "ekstra" nepoznatim silama koje zamjenjuju djelovanje udaljenih veza, što rezultira ekvivalentni sistem.
• 4. Da bi se osigurala ekvivalencija originalnog i glavnog sistema, nepoznate sile moraju biti odabrane tako da se deformacije glavnog sistema ne razlikuju od deformacija originalnog statički neodređenog sistema. U tu svrhu, pomjeranje tačaka primjene "suvišnih" nepoznanica u smjeru njihovog djelovanja izjednačeno je sa nulom. Iz dodatnih jednadžbi dobijenih na ovaj način određuju se vrijednosti "dodatnih" nepoznatih sila. Određivanje pomaka odgovarajućih tačaka može se izvršiti na bilo koji način, ali je bolje koristiti najopćenitiju Mohrovu metodu.
• 5. Nakon određivanja vrijednosti "ekstra" nepoznatih sila, određuju se reakcije i crtaju dijagrami unutrašnjih sila, odabiru presjeci i provjerava čvrstoća na uobičajen način.

Kanonske jednadžbe metode sila

Dodatne jednadžbe pomaka koje izražavaju jednakost nule pomaka u smjerovima "dodatnih" nepoznanica mogu se zgodno sastaviti u tzv. kanonski oblik one. prema određenom obrascu. Pokažimo to na primjeru rješavanja najjednostavnijeg statički neodređenog sistema (Sl. 47, a).

Odabiremo konzolu kao glavni sistem, odbacujući zglobni oslonac. Ekvivalentni sistem će se dobiti nakon primjene njegove vanjske sile T 7 i "ekstra" nepoznate X(Sl. 47, b).

Canonical Equation, koji izražava nulti pomak tačke AT od sila F i X, bice

Iz jednačine koju imamo

Za sistem koji ima dve "ekstra" veze, sistem kanonskih jednačina ima oblik:

• 8 11 X 1 + b 12 ^2 + ^1
• 621-^1 + 622^2 "I" ^20-

Pokreti A[p I b [y, uključeni u kanonske jednadžbe, određuju se Mohrovom metodom.

Za sisteme koji se sastoje od pravolinijskih elemenata, prikladno je izračunati pomake pomoću Vereshchaginove metode.

Na primjer, za zadatak prikazan na sl. 47, množenjem dijagrama (slika 48), dobijamo koeficijente kanonske jednačine:

1 2 I 3 1 I /I 2 1 5 I1 3

E]L LL =-/ / -/ = -, E]A LR =-------- +-------.

1 11 2 3 3 1 1R 2 2 2 2 3 2/ 48 E]

Get Chl - - = - E.

Definisanje snage X, zapravo smo pronašli reakciju podrške Ja sam za. Nadalje, problem određivanja faktora unutrašnjih sila može se, kao i obično, riješiti metodom presjeka.

MINISTARSTVO OBRAZOVANJA RUJSKE FEDERACIJE

DRŽAVNA INSTITUCIJA

DRŽAVNI TEHNIČKI UNIVERZITET KUZBAS

Odjel za čvrstoću materijala

PRORAČUN STATIČKI NEODREĐENIH SISTEMA ŠARKIRNIH ŠIPKA POD NAPENOM - KOMPRESIJOM

Smjernice za realizaciju računsko-grafičkog zadatka o čvrstoći materijala za studente svih specijalnosti

Sastavio: V.D. Moiseenko

Usvojen na sjednici Odjeljenja Zapisnik broj 8 od 29.06.01

Elektronska kopija se nalazi u biblioteci glavne zgrade KuzGTU-a

Kemerovo 2002

Uvod. Obim i svrha zadatka

Statički neodređeni sistem šarke i šipke je onaj u kojem se sile u šipkama i reakcije u osloncima ne mogu odrediti samo iz uslova ravnoteže.

Slika 1 prikazuje konvencionalni nosač koji se sastoji od dvije šipke. Sile N 1 i N 2 u štapovima ovog nosača lako se određuju iz uslova ravnoteže za sistem konvergentnih sila primenjenih na isečeni čvor C, pošto su rešene dve jednačine za ovaj sistem sila sa dve nepoznate.

Ako se dizajn konzole zakomplikuje dodavanjem još jednog štapa (slika 1, b), onda se sile u štapovima ne mogu odrediti na isti način, jer se za čvor C mogu sastaviti samo dvije jednadžbe statičke ravnoteže (ΣH = 0; ΣY = 0), a broj nepoznatih sila je tri. Jednom smo imali statički neodređen sistem.

Komplikovanjem dizajna i uvođenjem novih štapova, može se dobiti statički neodređen sistem dva puta (vidi sliku 1c), tri puta i tako dalje. Stoga se pod n puta statički neodređenim sistemom podrazumijeva takav sistem u kojem je broj veza veći od broja nezavisnih jednačina statike za n jedinica.

Dodatne jednadžbe potrebne za rješavanje problema mogu se naći razmatranjem sistema u deformiranom stanju i uspostavljanjem veza između pomaka i deformacija konstrukcijskih elemenata. Rezultirajuće jednačine se nazivaju jednadžbe kompatibilnosti deformacija.

Slika 2 prikazuje dijagrame nekih statički neodređenih sistema.

Fig.2. Neke vrste statički neodređenih sistema

Prilikom izučavanja dijela "Statički neodređeni sistemi štapa" i izvođenja ovog proračunsko-grafičkog zadatka student mora naučiti karakteristike statički neodređenih sistema; stječu vještine u otkrivanju statičke neodređenosti, u određivanju sila u elementima konstrukcije i odabiru površina poprečnog presjeka iz stanja čvrstoće.

Zadatak zahteva od studenta da uradi sledeće:

- odrediti sile u šipkama i odabrati površine poprečnog presjeka od djelovanja vanjskih opterećenja;

- odrediti dodatna naprezanja u šipkama zbog promjena temperature;

- odrediti dodatna montažna naprezanja uzrokovana nepreciznošću u izradi šipki;

- odaberite sekcije šipki prema graničnom stanju.

Obim i oblik izvođenja računskog i grafičkog zadatka zavise od obima predmeta koji se izučava i dogovara se od strane nastavnika na praktičnoj nastavi.

1. Kratke teorijske informacije

Prilikom rješavanja statički neodređenih problema treba se pridržavati sljedećeg redoslijeda:

1.1. Razmotrite statičku stranu problema. Napravite plan sila i napišite jednadžbe statike.

1.2. Razmotrite geometrijsku stranu problema. Napravite plan putovanja. Sastaviti dodatne jednadžbe kompatibilnosti deformacija u takvoj količini da se mogu pronaći sve nepoznate sile.

1.3. Razmotrite fizičku stranu problema. Prema zakonima fizike (sa proračunom temperature) i prema Hookeovom zakonu, izraziti deformacije u jednadžbama njihove kompatibilnosti kroz nepoznate sile koje djeluju u štapovima:

1.4. Izraditi zajedničko rješenje jednadžbi statike, geometrije, fizike i odrediti nepoznate sile.

1.5. Korišćenje uslova čvrstoće na pritisak ili zatezanje N/F = [ σ ], odaberite površine poprečnog presjeka šipki.

1.6. Uz poznate sile u šipkama i prihvaćene površine poprečnog presjeka, izračunajte normalne napone koristeći formulu

σ = N F .

2. Primjer

Dato: Apsolutno kruta greda AB počiva, kao što je prikazano na slici 3, opterećena ravnomjerno raspoređenim opterećenjem i silom P.

Fig.3. Dijagram statički neodređenog sistema

Početni podaci za proračun

4. Odredite ukupne napone u šipkama od djelovanja opterećenja, temperaturnih promjena i proizvodnih netočnosti.

2.1. Proračun statički neodređenog sistema šarki za vanjsko opterećenje

P = 30 kN q = 15 kN/m

A C B

Fig.4. Početna shema dizajna

2.1.1. Statička strana problema

Statička strana problema razmatra se planom sila. Plan sila je projektna shema koja prikazuje sve sile (i poznate i nepoznate) koje se primjenjuju na element sistema zglobnih šipki, čija se ravnoteža razmatra (u našem slučaju, to je kruta greda AB). Isjecimo čelične i bakrene šipke i zamijenimo njihove odbačene donje dijelove unutarnjim silama (sl. 5).

P = 30 kN q = 15 kN/m

A C B

60°

Rice. 5. Plan snaga od vanjskih opterećenja

Iz plana sila (vidi sliku 5) zapisujemo jednačine statičke ravnoteže. Da biste odgovorili na prvo pitanje problema, potrebno je poznavati sile u šipkama - čeliku i bakru. U ovom slučaju nema potrebe za izračunavanjem reakcije zglobnog nosača. Dakle od tri

moguće jednadžbe statike (ΣX = 0; ΣY = 0 ; Σm c = 0 ) zapisujemo

onaj koji ne uključuje reakcije osovine fiksiranog nosača C:

∑ mC = 0

− N CT a + q a 2 2 + p a + NM sin60o b = 0,

− N ST 2 + 15 2 2 2 + 30 2 − NM 0,866 4 = 0,

Nakon algebarskih operacija, jednadžba ravnoteže će poprimiti oblik

2.1.2. Geometrijska strana problema

Geometrijska strana problema razmatra se planom pomaka. Plan pomaka je projektni dijagram koji prikazuje položaj sistema šarki prije i poslije opterećenja. Na planu pomaka označavamo pomake tačaka grede (AA1 i BB1),

apsolutne deformacije bakrenih i čeličnih šipki (∆ l ST ; ∆ l M )

(Sl. 6). Štoviše, zbog malih deformacija pomičemo točke grede okomito gore ili dolje, a deformacije nagnutih šipki označavamo okomicom.

Rice. 6. Plan pomaka od djelovanja vanjskih opterećenja

Prema planu pomaka sastavljamo jednadžbu za kompatibilnost deformacija. Prije svega, zapisujemo omjer pomaka tačaka grede iz sličnosti trokuta AA1 C i CBB1 (slika 6):

Pomaci tačaka grede (AA1 i BB1) izraženi su kao deformacije

Izrazi (2.3) i (2.4) se zamjenjuju u relaciju (2.2):

2.1.3. Fizička strana problema

Rezultirajuća jednadžba kompatibilnosti deformacija (2.5) u ovom obliku ne može se riješiti s jednadžbom ravnoteže (2.1), jer su nepoznate veličine uključene u njih različite prirode.

Apsolutne deformacije ∆ l CT i ∆ l M u jednačini (2.5) izražavamo

Dobili smo jednadžbu kompatibilnosti deformacija napisanu u terminima sila u šipkama.

2.1.4. Sinteza

Riješimo zajedno jednadžbe ravnoteže (2.1) i jednadžbe kompatibilnosti deformacija (2.6).

NCT + 1,73 NM = 45

0,67NCT = 0,95NM.

Iz druge jednačine sistema izražavamo silu N ST:

i zamijeniti u prvu jednačinu sistema.

Pozitivni rezultat N ST i N M potvrđuje naše pretpostavke o kompresiji čelične šipke i napetosti bakrene šipke, što znači da će sile u šipkama biti:

2.1.5. Izbor poprečnih presjeka šipki

Odabir poprečnih presjeka šipki vrši se prema stanju vlačne čvrstoće - kompresije:

N F ≤ [σ] .

a) Površina poprečnog presjeka čelične šipke potrebna iz uvjeta čvrstoće će se odrediti:

b) Površina poprečnog presjeka bakrene šipke potrebna iz uvjeta čvrstoće će se odrediti:

U ovom slučaju, prema datom omjeru površina, površina čelične šipke treba biti jednaka:

FCT = 4 3 FM = 4 3 1,7 10- 4 = 1,275 10- 4 m2 ..

Prihvatamo velike površine poprečnog presjeka šipki:

Sa prihvaćenim površinama poprečnog presjeka bakrenih i čeličnih šipki određujemo napone u tim šipkama.

2.2. Proračun temperature statički neodređenog sistema šarke

Svrha proračuna temperature je određivanje dodatnih naprezanja u bakrenim i čeličnim šipkama zbog temperaturnih promjena.

Pretpostavimo da se sistem zagrijava za ∆ t = 20 o C . Algoritam rješenja ostaje isti. Početna shema dizajna prikazana je na sl. 7.

Sistemi šipki u kojima se reakcije potpore i unutrašnji faktori sile ne mogu pronaći samo iz jednačina ravnoteže nazivaju se statički neodređeno.

Razlika između broja potrebnih nepoznatih sila i nezavisnih jednadžbi ravnoteže određuje stepen statičke neodređenosti sistema. Stepen statičke neodređenosti uvijek je jednak broju redundantnih (suvišnih) veza čije uklanjanje pretvara statički neodređeni sistem u statički odrediv geometrijski nepromjenjiv sistem. I eksterne (referentne) veze i interne, koje nameću određena ograničenja kretanju sekcija sistema jedna u odnosu na drugu, mogu biti redundantne.

Geometrijski nepromjenjiv naziva se takav sistem čija je promjena oblika moguća samo u vezi sa deformacijama njegovih elemenata.

Geometrijski varijabilna naziva se takav sistem čiji se elementi mogu kretati pod djelovanjem vanjskih sila bez deformacije (mehanizam).

Prikazano na sl. 12.1 okvir ima sedam vanjskih (potpornih) veza. Da bi se odredile sile u ovim vezama (reakcije potpore), moguće je sastaviti samo tri nezavisne jednadžbe ravnoteže. Dakle, ovaj sistem ima četiri redundantne veze, što znači da je četiri puta statički neodređen. Dakle, stepen statičke nesigurnosti za ravne okvire je:

gdje R- broj reakcija podrške.

Kontura koja se sastoji od više elemenata (ravnih ili krivolinijskih) koji su međusobno kruto (bez šarki) spojenih i koji tvore zatvoreni krug naziva se zatvorenim krugom. . Pravougaoni okvir prikazan na slici 12.2 je zatvorena petlja. Ona je tri puta statički neodređena, jer da bi postala statički neodređena potrebno je odrezati jedan njen element i eliminisati tri dodatne veze. Reakcije ovih veza su: uzdužna sila, poprečna sila i moment savijanja koji djeluju na mjestu reza; ne mogu se odrediti pomoću jednačina statike. U sličnim uslovima, u smislu statičke neodređenosti, postoji bilo koja zatvorena petlja, koja uvek postoji triput statički neodređeno.

Uključivanje šarke u čvor okvira u kojem se spajaju dvije šipke, ili njegovo postavljanje na bilo koje mjesto na osi šipke, uklanja jednu vezu i smanjuje ukupni stupanj statičke neodređenosti za jedan. Takva šarka se naziva jednostruka ili jednostavna (slika 12.3).

Općenito, svaka šarka je uključena u čvor koji povezuje cšipke, smanjuje stepen statičke nesigurnosti c-1 , budući da se takva šarka zamjenjuje c-1 pojedinačne šarke (slika 12.3). Dakle, stepen statičke neodređenosti sistema u prisustvu zatvorenih petlji određuje se formulom.

Takav sistem se naziva statički neodređenim ako se ne može izračunati samo pomoću jednačina statike, jer ima nepotrebne veze. Za proračun takvih sistema sastavljaju se dodatne jednačine koje uzimaju u obzir deformacije sistema.

Statički neodređeni sistemi imaju niz karakterističnih karakteristika:

1. statički neodređeno strukture su čvršće od odgovarajućih statički određen, jer imaju dodatne priključke.
2. In statički neodređeno sistema, postoje manje unutrašnje sile, što određuje njihovu efikasnost u odnosu na statički određen sistema pod istim vanjskim opterećenjima.
3. Kršenje nepotrebnih veza u statički neodređeno sistema ne dovodi uvijek do uništenja, dok gubitak komunikacije u statički određen sistem ga čini geometrijski varijabilnim.
4. Za obračun statički neodređeno sistema, potrebno je prethodno specificirati geometrijske karakteristike poprečnih presjeka elemenata, tj. zapravo njihov oblik i veličinu, jer njihova promjena dovodi do promjene sila u vezama i nove raspodjele napora u svim elementima sistema.
5. Prilikom izračunavanja statički neodređeno sistema, potrebno je unaprijed odabrati materijal konstrukcije, jer je potrebno poznavati njegove module elastičnosti.
6. In statički neodređeno sistemi, temperaturni efekti, slijeganje nosača, nepreciznosti u izradi i ugradnji izazivaju dodatne napore.

Main metode izračunavanjastatički neodređeno sistemi su:

1. metoda sile. Ovdje se sile smatraju nepoznanicama - silama i momentima.
2.Metoda kretanja. Nepoznati su faktori deformacije - uglovi rotacije i linearni pomaci.
3.mešoviti metod. Ovdje dio nepoznanica predstavlja napore, a drugi dio predstavlja pomjeranja.
4. Kombinovana metoda. Koristi se u proračunu simetričnih sistema za asimetrična opterećenja. Ispada da je preporučljivo izračunati sistem za simetričnu komponentu datog opterećenja metodom pomaka, a za inverzno simetričnu komponentu - metodom sile.
Pored navedenih analitičkih metoda, u proračunu posebno složenih sistema koriste se različite numeričke metode.

Kanonske jednadžbe metode sila

Da biste dobili dodatne jednadžbe, koje su spomenute u prethodnom pasusu, morate prije svega okrenuti datu, n puta statički neodređeno sistem u statički određen uklanjanjem nepotrebnih veza iz njega. Rezultirajući statički određen sistem se zove osnovni. Imajte na umu da transformacija datog sistema u statički određen nije obavezna. Ponekad se koristi modifikacija metode sile u kojoj može biti osnovni sistem statički neodređeno, međutim, predstavljanje ovog pitanja je izvan okvira ovog priručnika. Uklanjanje bilo koje veze ne mijenja unutrašnje sile i deformacije sistema ako se na njega primjenjuju dodatne sile i momenti, a to su reakcije odbačenih veza. To znači da ako se dato opterećenje i reakcije udaljenih veza primjenjuju na glavni sistem, tada će glavni i dati sistemi postati ekvivalentno.

U datom sistemu ne može biti pomeranja duž pravca postojećih krutih karika, uključujući i one karike koje se odbacuju prilikom prelaska na glavni sistem, stoga u glavnom sistemu pomaci duž pravaca odbačenih karika moraju biti jednak nuli. A za to, reakcije ispuštenih veza moraju imati striktno definirane vrijednosti.

Uslov jednakosti nuli pomaka u pravcu bilo koje i-te veze od n odbačenog na osnovu principa nezavisnosti delovanja sila ima oblik:

pri čemu prvi indeks označava smjer kretanja i broj prekinute veze, a drugi razlog koji je izazvao kretanje, tj. je kretanje u smjeru i-te veze uzrokovano reakcijom k-te veze; - kretanje u pravcu i-te veze uzrokovano istovremenim djelovanjem cjelokupnog vanjskog opterećenja.

U metodi sile, reakcija k-te veze se obično označava sa Xk. Uzimajući u obzir ovu oznaku i zbog valjanosti Hookeovog zakona, pomaci se mogu predstaviti kao:

gdje je jedno (ili specifično) kretanje u smjeru i-te veze, uzrokovano reakcijom, tj. reakcija koja se poklapa u pravcu sa Xk, ali jednaka jedinici.

Zamjenom (2) u (1) dobijamo:

fizičko značenje jednačina (3): kretanje u glavnom sistemu u pravcu i-te odbačene veze je jednako nuli.

Zapisujući izraze slične (3) za cijeli skup odbačenih veza, dobijamo sistem kanonskih jednačinametoda sile:

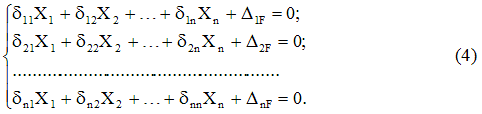
Oblik jednačine (4), tj. broj pojmova u svakom od njih i njihov ukupan broj određen je samo stepenom statičke neodređenosti sistema i ne zavisi od njegovih specifičnosti.

Koeficijenti sistema kanonskih jednadžbi (4) određuju se Mohr-Vereshchagin metodom množenjem odgovarajućih dijagrama. Svi ovi koeficijenti, kao što je gore navedeno, predstavljaju pomake; koeficijenti koji stoje na nepoznanicama su jedinični pomaci, a slobodni članovi jesu tereta. Pojedinačni pokreti se dijele na glavni, koji se nalaze duž glavne dijagonale i imaju iste indekse i nuspojave(). Glavni pokreti su uvijek pozitivni, za razliku od bočnih. Simetrično locirani pomaci, u skladu sa teoremom o uzajamnosti pomaka, međusobno su jednaki, tj. .

Algoritam za izračunavanje metode sile

Bez obzira na karakteristike razmatranog dizajna, može se razlikovati sljedeći redoslijed proračuna statički neodređenih sistema metoda sile:

1. Odredite stepen statičke nesigurnosti.
2. Odaberite glavni sistem.
3. Formirajte ekvivalentni sistem.
4. Zapalite sistem kanonske jednačine.
5. Konstruisati jedinične i dijagrame opterećenja faktora unutrašnjih sila koji nastaju u elementima razmatrane konstrukcije.
6. Izračunati koeficijente nepoznanica i slobodnih članova sistema kanonskih jednačina.
7. Izgradite ukupno jednu parcelu.
8. Izvršite univerzalnu provjeru koeficijenata za nepoznate i slobodne termine.
9. Riješiti sistem (4), tj. odrediti reakcije dodatnih veza.
10. Konstruirati dijagrame nastalih faktora unutrašnjih sila za dati sistem (drugim riječima, konačni dijagrami).
11. Izvršite statičke i kinematičke provjere.
Imajte na umu da tačke 7, 8, 11 gornjeg algoritma nisu apsolutno neophodne, iako vam omogućavaju kontrolu ispravnosti proračuna. A za sisteme sa jednom dodatnom vezom, tačke 7 i 8 su jednostavno besmislene, jer se u ovom slučaju ukupni pojedinačni dijagram poklapa sa jednim.
Pogledajmo bliže neke od gornjih koraka izračunavanja.

Odabir primarnog sistema

Ovo je najvažnija faza proračuna, jer racionalan izbor glavnog sistema uvelike pojednostavljuje rad na računanju. Razmotrimo moguće načine uklanjanja nepotrebnih veza, što određuje oblik glavnog sistema.

1. Odbacivanje nepotrebnih priključaka vrši se potpunim uklanjanjem pojedinih nosača ili njihovom zamjenom nosačima s manjim brojem priključaka. Reakcije koje djeluju u smjeru ispuštenih veza su redundantne nepoznanice. Na slici 1, b, c, d prikazane su različite verzije ekvivalentnog sistema dobijenog ovom metodom za okvir (slika 1, a).

2. Postavljanje šarki u srednjim dijelovima šipki omogućava da se u svakom takvom dijelu uspostavi veza koja odgovara momentu savijanja. Ovi trenuci su suvišne nepoznanice. Za okvir sa stepenom statičke neodređenosti n = 3 (sl. 2, a), pri izboru glavnog sistema moraju se ugraditi tri šarke. Položaj ovih šarki može biti proizvoljan, ali zadovoljavajući zahtjev geometrijske nepromjenjivosti sistema (slika 2b).

3. Disekcija štapa eliminiše tri veze koje odgovaraju unutrašnjim silama M, Q, N (slika 2, c). U posebnim slučajevima (slika 2d), sečenjem šipke duž šarke oslobađaju se dvije veze (sl. 2, e), a sečenjem ravne šipke sa šarkama na krajevima oslobađa se jedna veza (slika 2, f).

Među vezama statički neodređenog sistema razlikuju se apsolutno neophodne i uslovno neophodne. Apsolutno neophodne su karike čijim uklanjanjem sistem postaje geometrijski promenljiv. Apsolutno neophodnu vezu karakteriše statička odredivost napora u njoj, tj. reakcija takve veze može se izračunati iz uslova ravnoteže. Prilikom odabira glavnog sistema, apsolutno neophodne veze ne mogu se odbaciti.

Odnosi, nakon čijeg uklanjanja sistem i dalje ostaje geometrijski nepromijenjen, nazivaju se uslovno neophodnim. Sistem koji je prekinut može biti primarni sistem metoda sile.

Izračunavanje koeficijenata i slobodnih termina kanonskih jednačina

Ovoj fazi proračuna prethodi izrada dijagrama jedinica i opterećenja faktora unutrašnjih sila (za grede i okvire - dijagrami momenata savijanja). Jedinični dijagrami se konstruišu iz dejstva bezdimenzionalne jedinične sile ili bezdimenzionalnog jediničnog momenta, koji se poklapa u pravcu sa smerom odgovarajućeg viška nepoznatog u ekvivalentnom sistemu, i označavaju se sa , a jedinični dijagram sa .

Dijagram opterećenja je izgrađen od vanjskog opterećenja primijenjenog na glavni sistem. U ovom slučaju možete napraviti jedan dijagram od istovremenog djelovanja svih vanjskih opterećenja ili nekoliko dijagrama, odvojeno od svakog od primijenjenih opterećenja. Takva podjela jednog dijagrama opterećenja na nekoliko jednostavnijih, u pravilu je preporučljiva samo kada među postojećim opterećenjima postoji jedno ravnomjerno raspoređeno, a dijagram momenata u odgovarajućem presjeku ispod njega je predznak. U ovom slučaju, u svakoj kanonskoj jednadžbi, broj slobodnih članova će biti jednak broju ucrtanih dijagrama opterećenja.

Jedinični pomaci i pomaci opterećenja (koeficijenti i slobodni članovi kanonskih jednadžbi) se općenito mogu izračunati Mohrovom metodom. Za grede i okvire, to se može učiniti pomoću Vereshchaginovog pravila.

Univerzalna verifikacija koeficijenata i slobodnih termina kanonskih jednačina

Da biste izvršili univerzalnu provjeru, potrebno je izgraditi ukupni dijagram jedinice - dijagram momenata iz istovremenog djelovanja svih jediničnih sila primijenjenih na glavni sistem:

Ukupan pojedinačni dijagram množimo sa dijagramom:

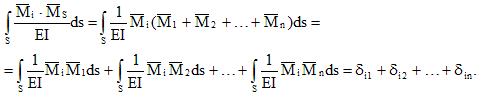
Dakle, rezultat množenja ukupnog i i-tog pojedinačnog dijagrama je kretanje u smjeru i-te veze od zajedničkog djelovanja pojedinačnih ekstra nepoznanica. Ovaj pomak je jednak zbiru koeficijenata i-te kanonske jednačine:

Ova provjera se zove red po red i važi za svaku kanonsku jednačinu.
Umjesto n linijskih provjera, najčešće se vrši jedna - univerzalni ček, koji se sastoji u množenju dijagrama ukupne jedinice sam po sebi i provjeri uvjeta:

Ako se izvrši univerzalna provjera, tada se pomaci jedinice izračunavaju ispravno; ako ne, potrebno je izvršiti provjere red po red, što će vam omogućiti da razjasnite pomak, prilikom čijeg izračunavanja je napravljena greška.

Za provjeru pomaka opterećenja potrebno je pomnožiti ukupne jedinične i dijagrame opterećenja momenata savijanja:

Dakle, verifikacija slobodnih članova sistema kanonskih jednačina (4) se sastoji u ispunjenju uslova.