Изчислете плоска статически неопределима прътова система. Изчисляване на статически неопределени системи по силов метод

Статично неопределените системи са прътови системи, в които само уравненията на равновесието не са достатъчни за определяне на реакциите на опорите. От кинематична гледна точка това са прътови системи, чийто брой степени на свобода е по-малък от броя на връзките. За да се разкрие статичната неопределеност на такива системи, е необходимо да се конструират допълнителни уравнения за съвместимост на деформациите. Броят на тези уравнения се определя от статичното число на неопределеност на прътовата система. Фигура 8.14 показва примери за статично неопределени греди и рамки.

Лъчът, показан на фиг. 8.14b, се нарича непрекъснатолъч. Това име идва от факта, че междинната опора поддържа само гредата. В точката на опора гредата не се врязва от пантата, пантата не се врязва в тялото на гредата. Следователно влиянието на напреженията и деформациите, които гредата изпитва върху левия участък, също засяга десния участък. Ако на мястото на междинната опора изрежем шарнир в тялото на гредата, то в резултат на това системата ще стане статично детерминирана - от една греда ще получим две независими една от друга греди, всяка от които ще бъде статично детерминирана . Трябва да се отбележи, че непрекъснатите греди са по-малко материалоемки от разделените греди, тъй като те по-рационално разпределят моментите на огъване по дължината си. В тази връзка непрекъснатите греди се използват широко в строителството и машиностроенето. Въпреки това, непрекъснатите греди, които са статично неопределени, изискват специална техника за изчисление, която включва използването на системни деформации.

Преди да започнете да изчислявате статично неопределени системи, е необходимо да се научите как да определяте степента на тяхната статична неопределеност. Едно от най-простите правила за определяне на степента на статична неопределеност е следното:

, (8.3)

Където  брой връзки, наложени върху конструкцията;  броя на възможните независими уравнения на равновесие, които могат да бъдат съставени за разглежданата система.

Нека използваме уравнение (8.3), за да определим степента на статична неопределеност на системите, изобразени на фиг. 8.14.

Гредата, показана на фиг. 8.14a, е веднъж статично неопределена, тъй като има три връзки на лявата опора и една връзка на дясната опора. За такъв лъч могат да бъдат конструирани само три независими уравнения на равновесие. По този начин степента на статична неопределеност на лъча
. Непрекъснатата греда, показана на фиг. 8.14b, също е веднъж статично неопределена, тъй като има две връзки на лявата опора и по една връзка на междинната опора и на дясната опора - общо четири връзки. По този начин степента на неговата статична неопределеност
.

Рамката, показана на фиг. 8.14c, е три пъти статично неопределен, тъй като има шест връзки в опорите. За тази рамка могат да бъдат конструирани само три независими уравнения на равновесие. По този начин степента на статична неопределеност за тази рамка от уравнение (8.3) е равна на:
. Степента на статична неопределеност на рамката, показана на фиг. 8.18d, е равна на четири, тъй като рамката има седем връзки на опорите. Следователно степента на неговата статична неопределеност е равна на
.

Правилото (8.3) за определяне на степента на статична неопределеност се използва само за прости системи. В по-сложни случаи това правило не работи. Фигура 8.15 показва рамка, чиято степен на статична неопределеност не може да бъде определена с помощта на уравнение (8.3).

Външно системата, показана на фигура 8.15, е статично неопределена пет пъти. Това може лесно да се установи с помощта на уравнение (8.3): от шест външни връзки (три в раздел A, три в раздел B и две в раздел C) се изваждат три възможни уравнения на равновесие. Тази система обаче има и вътрешна статична неопределеност. Невъзможно е да се вземе предвид вътрешната статична неопределеност, като се използва уравнение (8.3). Преди да преминем към определяне на степента на статична неопределеност на рамката, показана на фиг. 8.15, въвеждаме няколко определения. Първата от тези дефиниции включва концепцията за проста панта.

простонаречена панта, свързваща два пръта (фиг. 8.16).

Фиг.8.16. Обикновена панта

Нарича се панта, свързваща няколко пръта комплекс(фиг.8.17).

Фиг.8.17. Комплексна панта

Броят на простите панти, които могат да заменят една сложна панта, се определя от формулата:

, (8.4)

Където
- брой пръти, включени в комплекта.

Нека преизчислим сложната панта, показана на фиг. 8.17, в броя на простите панти, използвайки формула (8.4):
. Така сложната панта, показана на фиг. 8.17, може да бъде заменена с четири прости панти.

Нека въведем още едно понятие - затворен контур.

Нека докажем теоремата: всеки затворен контур е три пъти статически неопределен.

За да докажете теоремата, разгледайте затворен контур, натоварен с външни сили (фиг. 8.18).

Нека изрежем затворен контур с вертикално сечение и да покажем вътрешните силови фактори, които възникват при сечението. Във всяка секция възникват три вътрешни фактора: сила на срязване , момент на огъване
и надлъжна сила
. Общо върху всяка от отрязаните части на контура, в допълнение към външните сили, действат шест вътрешни фактора (фиг. 8.18, b, c). Като се има предвид равновесието на една от отсечените части, например лявата (фиг. 8.18, b), откриваме, че проблемът е три пъти статично неопределен, тъй като за отсечената част е възможно да се конструира само три независими уравнения на равновесие и има шест неизвестни сили, действащи върху граничната част. По този начин степента на статична неопределеност на затворен контур е равна на
. Теоремата е доказана.

Сега, използвайки концепцията за проста панта и затворен контур, можем да формулираме друго правило за определяне на степента на статична неопределеност:

, (8.5)

Където
 брой затворени контури;
 брой панти по отношение на прости (8.4).

Използвайки уравнение (8.5), определяме степента на статична неопределеност на рамката, показана на фиг. 8.15. Рамката има пет контура
, включително контура, образуван от опорните пръти. Пантата във възел D е проста, тъй като свързва два пръта. Пантата в секция K е сложна, защото свързва четири пръта. Броят на простите панти, които могат да заменят пантата в секция K, е равен по формула (8.4):
. Панта C също е сложна, защото свързва три пръта. За тази панта
. Освен това системата има още две прости панти, с които се захваща за основата. По този начин броят на простите панти в системата е равен на
. Заместване на броя на затворените контури
и броя на простите панти
във формула (8.5) определяме степента на статична неопределеност на рамката:
. Така, показаното на фиг. 8.15 кадър, седем пъти статично неопределен. Това означава, че за изчисляване на такава система е необходимо да се съставят, в допълнение към трите уравнения на равновесието, седем уравнения за съвместимост на деформациите. Чрез решаването на така получената система от 10 уравнения за неизвестните, включени в тези уравнения, е възможно да се определи както големината на реакциите във външните връзки, така и вътрешните сили, възникващи в рамката. Процедурата за решаване на този проблем може да бъде донякъде опростена чрез елиминиране на уравненията на равновесието от системата от уравнения. Този подход обаче изисква използването на специални методи за решаване, един от които е методът на силите.

Статично неопределени системи са тези системи, в които вътрешните сили не могат да се определят само от уравненията на равновесието (статични уравнения).

Статически неопределените конструкции имат т.нар екстракомуникации. Те могат да се появят в опори, пръти и други елементи. Такива връзки се наричат ​​"излишни", защото не са необходими за осигуряване на баланса на конструкцията, а се определят от изискванията за нейната здравина и твърдост. Такива допълнителни връзки се наричат външен.Освен това могат да възникнат ненужни връзки поради особеностите на самия дизайн. Например затворен контур на рамка (фиг. 46, G)има три неизвестни вътрешни сили във всяко сечение, т.е. те са общо шест, като три от тях са „екстра“. Това допълнително усилие се нарича вътрешни.Въз основа на броя на външните или вътрешните „допълнителни“ връзки, които те установяват степента на статична неопределеност на системата.То е равно на разликата между броя на неизвестните, които трябва да се определят, и броя на статичните уравнения. С едно “допълнително” неизвестно системата се нарича веднъж или веднъж статично неопределена, с две - два пъти статично неопределена и т.н.

Дизайнът, показан на фиг. 46, А, веднъж е статично неопределен и структурите, показани на фиг. 46, bИ V, -два пъти статично неопределени, на фиг. 46, g - три пъти със статически неопределен строеж.

При решаване на статически неопределени задачи в допълнение към статичните уравнения се използват уравнения, които отчитат деформациите на конструктивните елементи.

Има няколко метода за решаване на статично неопределени проблеми: метод за сравнение на изместване, метод на силата, метод на изместване.

Силов метод

При изчисляване на статично неопределени системи силите се приемат като неизвестни.

Изчисляване по силов методизвършва в следната последователност:

• 1. Установете степента на статична неопределеност.
• 2. Чрез премахване на „допълнителните“ връзки, заменете оригиналната система със статично дефинируема, т.нар. основна система.Могат да се изградят няколко такива системи, като се спазва състоянието на тяхната геолокация

метрична неизменност.

• 3. Основната система е натоварена с дадени външни сили и „допълнителни“ неизвестни сили, които заместват действието на отдалечени връзки, което води до еквивалентна система.
• 4. За да се осигури еквивалентността на оригиналната и основната системи, неизвестните сили трябва да бъдат избрани така, че деформациите на основната система да не се различават от деформациите на оригиналната статично неопределена система. За това движение на точките на приложение „допълнителните“ неизвестни в посоката на тяхното действие са равни на нула. От получените по този начин допълнителни уравнения се определят стойностите на „допълнителните“ неизвестни усилия. Определянето на преместванията на съответните точки може да стане по всякакъв начин, но е по-добре да се използва най-общият метод на Мор.
• 5. След определяне на стойностите на „допълнителните“ неизвестни сили се определят реакциите и се изграждат диаграми на вътрешните сили, се избират секции и се проверява якостта по обичайния начин.

Канонични уравнения на силовия метод

Допълнителни уравнения на преместване, изразяващи равенството на нула на преместване в посоките на „допълнителните“ неизвестни, са удобно съставени в т.нар. канонична форма,тези. по определен модел. Нека покажем това, като използваме примера за решаване на най-простата статично неопределена система (фиг. 47, А).

Нека изберем конзолата като основна система, като изхвърлим опората на пантата. Получаваме еквивалентна система след прилагане на нейната външна сила T 7 и „допълнителното“ неизвестно х(Фиг. 47, б).

Канонично уравнение, изразяваща равенството на преместването на точката на нула INот силите на Ф Х,ще

От уравнението, което имаме

За система, която има две „допълнителни“ връзки, системата от канонични уравнения има формата:

• 8 11 X 1 + b 12 ^2 + ^1
• 621-^1 + 622^2 "I" ^20-

Движения A[rИ b[y, включени в каноничните уравнения, се определят по метода на Мор.

За системи, състоящи се от праволинейни елементи, е удобно да се изчислят преместванията по метода на Верещагин.

Например, за проблема, показан на фиг. 47, умножавайки диаграмите (фиг. 48), получаваме коефициентите на каноничното уравнение:

1 2 I 3 1 I/I 2 1 5 I1 3

E]b LL =-/ / -/ = -, E]A LR =-------- +-------.

1 11 2 3 3 1 1Р 2 2 2 2 3 2/ 48 E]

Получаваме Хл - - = - д.

След като определи силата Х,всъщност открихме реакцията на подкрепата Аз съм в.След това проблемът за определяне на вътрешните силови фактори може да бъде решен, както обикновено, с помощта на метода на сечението.

МИНИСТЕРСТВО НА ОБРАЗОВАНИЕТО НА РУСКАТА ФЕДЕРАЦИЯ

ДЪРЖАВНА ИНСТИТУЦИЯ

КУЗБАСКИ ДЪРЖАВЕН ТЕХНИЧЕСКИ УНИВЕРСИТЕТ

Катедра Съпротивление на материалите

ИЗЧИСЛЯВАНЕ НА СТАТИЧЕСКИ НЕОПРЕДЕЛЕНИ ШАРНИРНИ СИСТЕМИ ПРИ НАПЪН-КОМПРЕСИЯ

Указания за изпълнение на изчислителни и графични задачи по якост на материалите за студенти от всички специалности

Съставител: V.D. Моисеенко

Приет на заседание на катедрата Протокол № 8 от 29.06.2001г

Електронно копие се намира в библиотеката на главната сграда на държавния университет KuzSTU

Кемерово 2002г

Въведение. Обхват и цел на заданието

Статично неопределена шарнирно-прътова система е тази, при която силите в прътите и реакциите в опорите не могат да се определят само от условието на равновесие.

Фигура 1 показва конвенционална скоба, състояща се от два пръта. Силите N 1 и N 2 в прътите на тази скоба се определят лесно от условието за равновесие на системата от сближаващи се сили, приложени към изрязания възел C, тъй като се решават две уравнения за тази система от сили с две неизвестни.

Ако конструкцията на скобата е усложнена чрез добавяне на друг прът (фиг. 1, b), тогава силите в прътите не могат да бъдат определени по същия начин, тъй като за възел C все още е възможно да се създадат само две уравнения на статично равновесие ( ΣХ = 0; ΣY = 0), а броят на неизвестните усилия е три. Имаме веднъж статично неопределена система.

Чрез усложняване на дизайна и въвеждане на нови пръти е възможно да се получи статично неопределена система два пъти (виж фиг. 1, в), три пъти и т.н. Следователно, под n пъти статично неопределена система имаме предвид система, в която броят на връзките надвишава броя на независимите статични уравнения с n единици.

Допълнителните уравнения, необходими за решаване на проблема, могат да бъдат намерени чрез разглеждане на системата в деформирано състояние и установяване на връзки между преместванията и деформациите на структурните елементи. Получените уравнения се наричат ​​уравнения за съвместимост на деформациите.

Фигура 2 показва диаграми на някои статично неопределени системи.

Фиг.2. Някои видове статично неопределени системи

При изучаване на раздела „Статично неопределени прътови системи“ и изпълнение на тази изчислителна и графична задача студентът трябва да научи характеристиките на статически неопределените системи; придобиват умения за разкриване на статична неопределеност, определяне на сили в структурни елементи и избор на площи на напречно сечение от якостни условия.

В задачата студентът трябва да изпълни следната работа:

- определят силите в прътите и избират площите на напречното сечение от действието на външни натоварвания;

- определяне на допълнителни напрежения в прътите поради температурни промени;

- определят допълнителни инсталационни напрежения, причинени от неточно производство на пръти;

- изберете напречни сечения на пръти според граничното състояние.

Обемът и формата на изпълнение на изчислителната и графичната задача зависят от обема на изучавания курс и се обсъждат от преподавателя по време на практическите занятия.

1. Кратка теоретична информация

При решаване на статично неопределени задачи трябва да се спазва следният ред:

1.1. Помислете за статичната страна на проблема. Изградете план на силите и съставете статични уравнения.

1.2. Помислете за геометричната страна на проблема. Изградете план за пътуване. Създайте допълнителни уравнения за съвместимост на деформациите в такова количество, че да могат да бъдат намерени всички неизвестни сили.

1.3. Помислете за физическата страна на проблема. Съгласно законите на физиката (при температурни изчисления) и според закона на Хук, изразете деформациите в уравненията на тяхната съвместимост чрез неизвестни сили, действащи в прътите:

1.4. Извършете съвместно решение на уравненията на статиката, геометрията, физиката и определете неизвестните сили.

1.5. Използване на условия за якост на натиск или опън N/F = [σ], изберете площите на напречното сечение на прътите.

1.6. С известни сили в прътите и приети площи на напречното сечение, изчислете нормалните напрежения, като използвате формулата

σ = N F .

2. Пример

Дадено: Абсолютно твърда греда AB се поддържа, както е показано на фиг. 3, натоварена с равномерно разпределен товар и сила P.

Фиг.3. Диаграма на статично неопределена система

Изходни данни за изчисление

4. Определете общите напрежения в прътите поради натоварвания, температурни промени и производствени неточности.

2.1. Изчисляване на статично неопределена система от шарнирни пръти за външно натоварване

P = 30 kN q = 15 kN/m

A C B

Фиг.4. Първоначална изчислителна схема

2.1.1. Статична страна на проблема

Статичната страна на проблема се разглежда от силовия план. Силовият план е изчислителна диаграма, която показва всички сили (както известни, така и неизвестни), приложени към елемента на системата шарнир-пръчка, чието равновесие се разглежда (в нашия случай това е твърдата греда AB). Нека срежем стоманените и медните пръти и заменим изхвърлените им долни части с вътрешни сили (фиг. 5).

P = 30 kN q = 15 kN/m

A C B

60°

Ориз. 5. План на силите от външни натоварвания

От плана на силите (виж фиг. 5) записваме уравненията на статичното равновесие. За да отговорите на първия въпрос от задачата, трябва да знаете силите в прътите - стомана и мед. В този случай не е необходимо да се изчислява реакцията на шарнирната неподвижна опора. Следователно от три

възможни статични уравнения (ΣX = 0; ΣY = 0; Σm c = 0) записваме

такава, която не включва реакциите на шарнирно-фиксираната опора C:

∑ mC = 0

− N CT a + q a 2 2 + p a + NM sin60o b = 0,

− N ST 2 + 15 2 2 2 + 30 2 − NM 0,866 4 = 0,

След алгебрични операции уравнението на равновесието приема формата

2.1.2. Геометрична страна на проблема

Геометричната страна на проблема се разглежда от плана за изместване. Планът за изместване е изчислителна диаграма, която показва позицията на системата шарнир-щанга преди и след натоварване. На плана за движение посочваме движенията на точките на лъча (AA1 и BB1),

абсолютни деформации на медни и стоманени пръти (∆ l ST; ∆ l M)

(фиг. 6). Освен това, поради малки деформации, ние преместваме точките на лъча вертикално нагоре или надолу и маркираме деформациите на наклонените пръти с перпендикуляр.

Ориз. 6. План на преместванията от външни натоварвания

Използвайки плана на изместване, съставяме уравнение за съвместимост на деформацията. Първо, нека запишем съотношението на преместванията на точките на лъча от подобието на триъгълници AA1 C и CBB1 (фиг. 6):

Изразяваме преместванията на точките на гредата (AA1 и BB1) чрез деформации

Заменяме изрази (2.3) и (2.4) във връзка (2.2):

2.1.3. Физическата страна на проблема

Полученото уравнение за деформационна съвместимост (2.5) в тази форма не може да бъде решено с уравнението на равновесието (2.1), тъй като неизвестните величини, включени в тях, са от различно естество.

Абсолютните деформации ∆ l CT и ∆ l M в уравнение (2.5) могат да бъдат изразени

Получихме уравнение за съвместимостта на деформациите, написано чрез силите в прътите.

2.1.4. Синтез

Нека решим заедно уравнението на равновесието (2.1) и уравнението за съвместимост на деформациите (2.6).

NCT + 1.73NM = 45

0.67NCT = 0.95NM.

От второто уравнение на системата изразяваме силата N ST:

и го заместете в първото уравнение на системата.

Положителният резултат от N ST и N M потвърждава нашите предположения за натиск на стоманения прът и опън на медния прът, което означава, че силите в прътите ще бъдат:

2.1.5. Избор на напречни сечения на пръти

Изборът на напречни сечения на пръти се извършва според условията на якост на опън - компресия:

N F ≤ [σ] .

а) Ще се определи площта на напречното сечение на стоманения прът, изисквана от състоянието на якост:

б) Ще се определи площта на напречното сечение на медния прът, изисквана от състоянието на якост:

В този случай, според даденото съотношение на площта, площта на стоманения прът трябва да бъде равна на:

FST = 4 3 FM = 4 3 1,7 10− 4 = 1,275 10− 4 m2 ..

Приемаме пръти с големи напречни сечения:

Като се имат предвид приетите площи на напречното сечение на медните и стоманените пръти, ние определяме напреженията в тези пръти.

2.2. Температурно изчисляване на статично неопределена система шарнир-щанга

Целта на изчисляването на температурата е да се определят допълнителни напрежения в медни и стоманени пръти, дължащи се на температурни промени.

Да приемем, че системата се нагрява с ∆ t = 20 o C. Алгоритъмът за решение остава същият. Първоначалната проектна диаграма е показана на фиг. 7.

Наричат ​​се прътови системи, опорни реакции и фактори на вътрешна сила, в които не могат да бъдат намерени само от уравненията на равновесието статически неопределени.

Разликата между броя на неизвестните неизвестни сили и независимите уравнения на равновесието определя степен на статична неопределеност на системата. Степента на статична неопределеност винаги е равна на броя на излишните (излишни) връзки, премахването на които превръща статично неопределената система в статично определима геометрично непроменлива система. Както външните (поддържащи) връзки, така и вътрешните могат да бъдат излишни, налагайки определени ограничения върху движението на системните секции един спрямо друг.

Геометрично непроменливе система, чиято форма може да се промени само поради деформации на нейните елементи.

Геометрично променливае система, чиито елементи могат да се движат под въздействието на външни сили без деформация (механизъм).

Показано на фиг. 12.1 рамката има седем външни (поддържащи) връзки. За да определите силите в тези връзки (опорни реакции), можете да създадете само три независими уравнения на равновесие. Следователно тази система има четири излишни връзки, което означава, че е статично неопределена четири пъти. По този начин степента на статична неопределеност за плоски рамки е равна на:

Където Р- брой реакции на поддръжка.

Контур, състоящ се от редица елементи (прави или извити), твърдо (без панти), свързани помежду си и образуващи затворена верига, се нарича затворен . Правоъгълната рамка, показана на фигура 12.2, е затворен контур. Той е три пъти статично неопределен, тъй като за да се трансформира в статично дефинируем е необходимо да се изреже един от неговите елементи и да се премахнат три допълнителни връзки. Реакциите на тези връзки са: надлъжна сила, напречна сила и огъващ момент, действащи в мястото на срязване; те не могат да бъдат определени с помощта на статични уравнения. При подобни условия, в смисъл на статична неопределеност, има всеки затворен контур, който е винаги три пъти статично неопределени.

Включването на шарнир в рамката, в която се срещат два пръта, или поставянето му навсякъде по оста на пръта, премахва една връзка и намалява общата степен на статична неопределеност с една. Такава панта се нарича единична или проста (фиг. 12.3).

Като цяло, всяка панта, включена в свързващ възел ° Спръти, намалява степента на статична несигурност с ° С-1 , тъй като такава панта замества ° С-1 единични панти (фиг. 12.3). По този начин степента на статична неопределеност на системата при наличие на затворени контури се определя от формулата.

Статично неопределена е система, която не може да бъде изчислена само с помощта на статични уравнения, тъй като има ненужни връзки. За изчисляване на такива системи се съставят допълнителни уравнения, които отчитат деформациите на системата.

Статично неопределени системиимат редица характерни черти:

1. Статично неопределенконструкциите са по-твърди от съответните статично определими, тъй като имат допълнителни връзки.
2. Б статически неопределенисистеми имат по-малко вътрешни сили, което определя тяхната ефективност в сравнение с статично определими системи при еднакви външни натоварвания.
3. Прекъсване на ненужни връзки статически неопределенисистема не винаги води до разрушаване, докато загубата на комуникация в статично определимисистема го прави геометрично променлив.
4. За изчисление статически неопределенисистемите трябва първо да бъдат определени от геометричните характеристики на напречните сечения на елементите, т.е. всъщност тяхната форма и размер, тъй като тяхното изменение води до промяна на силите във връзките и ново разпределение на силите във всички елементи на системата.
5. При изчисляване статически неопределенисистеми е необходимо предварително да се избере строителният материал, тъй като е необходимо да се знаят неговите еластични модули.
6. Б статически неопределенисистеми, температурни ефекти, утаяване на опори, неточности в производството и монтажа причиняват допълнителни сили.

Основен методи за изчислениестатически неопределенисистеми са:

1. Силов метод. Тук усилията - сили и моменти - се считат за неизвестни.
2.Метод на движение.Неизвестни са факторите на деформация - ъгли на завъртане и линейни премествания.
3.Смесен метод.Тук част от неизвестните представлява усилие, а другата част представлява изместване.
4. Комбиниран метод.Използва се при изчисляване на симетрични системи за асиметрични натоварвания. Оказва се, че е препоръчително системата да се изчислява за симетричната компонента на дадено натоварване по метода на преместването, а за обратно симетричната компонента по метода на силата.
В допълнение към горните аналитични методи, различни числени методи се използват при изчисляване на особено сложни системи.

Канонични уравнения на силовия метод

За да получите допълнителни уравнения, обсъдени в предишния параграф, трябва първо да трансформирате дадените n пъти статически неопределенисистема в статично детерминирана, като премахнете ненужните връзки от нея. Получената статично дефинируема система се нарича основен.Имайте предвид, че трансформирането на дадена система в статично определима не е необходимо. Понякога се използва модификация на силовия метод, в който може да бъде основната система статически неопределени, но представянето на този проблем е извън обхвата на това ръководство. Премахването на всякакви връзки не променя вътрешните сили и деформации на системата, ако към нея се прилагат допълнителни сили и моменти, които са реакции на изхвърлените връзки. Това означава, че ако дадено натоварване и реакции на отдалечени връзки се приложат към основната система, тогава основната и дадените системи ще станат еквивалентен.

В дадена система не може да има движения в посоките на съществуващите твърди връзки, включително тези връзки, които са били изхвърлени по време на прехода към основната система, следователно в основната система движенията в посоките на изхвърлените връзки трябва да бъдат равно на нула. И за това реакциите на изхвърлените връзки трябва да имат строго определени стойности.

Условието за нулево изместване по посока на всяка i-та връзка от n, отхвърлена на базата на принципа на независимост от действието на силите, има формата:

където първият индекс означава посоката на движение и номера на изхвърлената връзка, а вторият показва причината, предизвикала движението, т.е. е движението в посока на i-тата връзка, причинено от реакцията на k-тата връзка; - движение в посока на i-тата връзка, причинено от едновременното действие на целия външен товар.

При силовия метод реакцията на k-та връзка обикновено се означава с Xk. Като се има предвид това обозначение и поради валидността на закона на Хук, преместванията могат да бъдат представени като:

където е единично (или специфично) движение в посока на i-тата връзка, причинено от реакцията, т.е. реакция, съвпадаща по посока с Xk, но равна на единица.

Замествайки (2) в (1), получаваме:

Физически смисълуравнение (3): движението в основната система в посока на i-тото изхвърлено съединение е нула.

Пишейки изрази, подобни на (3) за целия набор от изхвърлени връзки, получаваме система от канонични уравнениясилов метод:

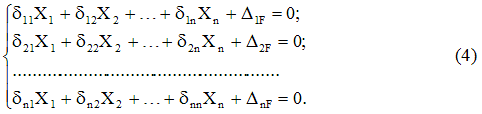
Формата на уравнение (4), т.е. броят на термините във всеки от тях и общият им брой се определят само от степента на статична неопределеност на системата и не зависят от нейните специфични особености.

Коефициентите на системата от канонични уравнения (4) се определят по метода на Мор-Верещагин чрез умножаване на съответните диаграми. Всички тези коефициенти, както е посочено по-горе, представляват премествания; коефициентите, свързани с неизвестните, са единични измествания, а свободните членове са товари.Единичните движения се разделят на основните,разположени по главния диагонал и имащи еднакви индекси и страна(). Основните движения винаги са положителни, за разлика от второстепенните. Симетрично разположените премествания в съответствие с теоремата за реципрочността на преместванията са равни помежду си, т.е. .

Алгоритъм за изчисление по метода на силата

Независимо от характеристиките на разглеждания дизайн, можем да различим следната последователност от изчисления за статично неопределени системи силов метод:

1. Дефинирайте степен на статична неопределеност.
2. Изберете основната система.
3. Формирайте еквивалентна система.
4. Запишете системата канонични уравнения.
5. Изграждане на възлови и натоварващи диаграми на вътрешните силови фактори, възникващи в елементите на разглежданата конструкция.
6. Изчислете коефициентите на неизвестните и свободните членове на системата от канонични уравнения.
7. Постройте обща единична диаграма.
8. Извършете универсална проверка на коефициенти за неизвестни и свободни членове.
9. Решете система (4), т.е. определят реакциите на допълнителни връзки.
10. Изградете диаграми на възникващи вътрешни силови фактори за дадена система (с други думи, окончателни диаграми).
11. Извършете статични и кинематични проверки.
Имайте предвид, че точки 7, 8, 11 от горния алгоритъм не са абсолютно необходими, въпреки че ви позволяват да контролирате правилността на изчислението. А за системи с една допълнителна връзка, точки 7 и 8 са просто безсмислени, тъй като в този случай общата блокова диаграма съвпада с блоковата.
Нека се спрем по-подробно на някои от горните етапи на изчисление.

Избор на първична система

Това е най-важният етап от изчислението, тъй като рационалният избор на основната система значително опростява изчислителната работа. Нека разгледаме възможните начини за премахване на ненужните връзки, което определя вида на основната система.

1. Премахването на ненужните връзки се извършва чрез пълно премахване на някои опори или замяната им с опори с по-малко връзки. Реакциите, действащи по посока на изхвърлените връзки, са допълнителни неизвестни. Фигура 1, b, c, d показва различни версии на еквивалентната система, получена по този метод за рамката (Фигура 1, a).

2. Поставянето на панти в междинните секции на прътите позволява да се установи връзка, съответстваща на огъващия момент във всяка такава секция. Тези моменти са ненужни неизвестни. За рамка със степен на статична неопределеност n=3 (фиг. 2, а) при избора на основната система е необходимо да се монтират три панти. Позицията на тези панти може да бъде произволна, но да отговаря на изискването за геометрична неизменност на системата (фиг. 2, b).

3. Нарязването на пръта премахва три връзки, съответстващи на вътрешните сили M, Q, N (фиг. 2, c). В частни случаи (фиг. 2, г) разрязването на пръчка по дължината на пантата освобождава две връзки (фиг. 2, д), а разрязването на права пръчка с панти в краищата освобождава една връзка (фиг. 2, е).

Сред връзките на статично неопределена система се прави разлика между абсолютно необходими и условно необходими. Абсолютно необходимите връзки включват тези връзки, които, когато бъдат премахнати, правят системата геометрично променлива. Абсолютно необходимата връзка се характеризира със статичната определимост на усилието в нея, т.е. реакцията на такава връзка може да се изчисли от условието за равновесие. При избора на основната система абсолютно необходимите връзки не могат да бъдат изхвърлени.

Връзките, при премахване на които системата продължава да остава геометрично непроменена, се наричат ​​условно необходими. Системата, от която е премахната такава връзка, може да бъде основната система силов метод.

Изчисляване на коефициенти и свободни членове на канонични уравнения

Този етап на изчисление се предхожда от изграждането на блокови и натоварващи диаграми на вътрешните силови фактори (за греди и рамки - диаграми на огъващи моменти). Единичните диаграми се изграждат от действието на безразмерна единична сила или безразмерен единичен момент, съвпадащи по посока с посоката на съответното допълнително неизвестно в еквивалентната система, и се означават с , а единичната диаграма с .

Диаграмата на натоварването е изградена от външен товар, приложен към основната система. В този случай можете да изградите една диаграма от едновременното действие на всички външни натоварвания или няколко диаграми, отделно от всяко от приложените натоварвания. Такова разделяне на една диаграма на натоварване на няколко по-прости по правило е препоръчително само когато сред действащите натоварвания има равномерно разпределен, а диаграмата на моментите в съответния участък под него се редува по знак. В този случай във всяко канонично уравнение броят на свободните членове ще бъде равен на броя на построените диаграми на натоварване.

Единични и товарни премествания (коефициенти и свободни членове на каноничните уравнения) в общия случай могат да се изчислят по метода на Мор. За греди и рамки това може да се направи с помощта на правилото на Vereshchagin.

Универсална проверка на коефициенти и свободни членове на канонични уравнения

За извършване на универсална проверка е необходимо да се изгради обща блокова диаграма - диаграма на моментите от едновременното действие на всички единични сили, приложени към основната система:

Нека умножим диаграмата на общата единица с диаграмата:

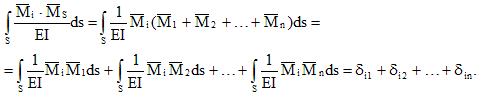
По този начин резултатът от умножаването на общата и i-тата единична диаграма е движение в посока на i-тата връзка от съвместното действие на отделни допълнителни неизвестни. Това изместване е равно на сумата от коефициентите на i-тото канонично уравнение:

Тази проверка се нарича ред по реди е изпълнено за всяко канонично уравнение.
Вместо n проверки ред по ред, най-често се извършва една - универсална проверка,което се състои от умножаване на диаграмата на общата единица сама по себе си и проверка на условието:

Ако универсалната проверка е извършена, тогава движенията на единиците са изчислени правилно; ако не, е необходимо да се извършат проверки ред по ред, което ще позволи да се изясни движението, при чието изчисляване е допусната грешка.

За да проверите движенията на товара, е необходимо да умножите общата единица и диаграмите на натоварване на моментите на огъване:

По този начин проверката на свободните членове на системата от канонични уравнения (4) се състои в изпълнение на условието.