Pojem funkcije, lastnosti funkcije, grafika funkcij. Osnovni pojmi in lastnosti funkcij

Funkcije in njihove lastnosti

Funkcija je eden najpomembnejših matematičnih konceptov.funkcija Imenujejo tako odvisnost spremenljivke y od spremenljivke x, pri kateri vsaki vrednosti spremenljivke x ustreza ena sama vrednost spremenljivke y.

Spremenljivka X klical neodvisna spremenljivka oz prepir. Spremenljivka pri klical odvisna spremenljivka. To tudi pravijospremenljivka y je funkcija spremenljivke x. Vrednosti odvisne spremenljivke se imenujejofunkcijske vrednosti.

Če je odvisnost spremenljivkepri iz spremenljivkeX je funkcija, potem jo lahko na kratko zapišemo takole:l= f( x ). (Preberite:pri enakof odX .) Simbolf( x) označujejo vrednost funkcije, ki ustreza vrednosti argumenta, ki je enakX .

Vse vrednosti neodvisne spremenljivke tvorijodomena funkcije . Vse vrednosti, ki jih ima odvisna spremenljivkaobseg delovanja .

Če je funkcija podana s formulo in njena definicijska domena ni določena, se šteje, da je definicijska domena funkcije sestavljena iz vseh vrednosti argumenta, za katere je formula smiselna.

Metode za določanje funkcije:

1.analitična metoda (funkcija je podana z uporabo matematična formula;

2.tabelarna metoda (funkcija je podana s tabelo)

3.opisna metoda (navedena je funkcija besedni opis)

4. grafična metoda (funkcija je podana z grafom).

Funkcijski graf poimenujte množico vseh točk koordinatne ravnine, katerih abscise so enake vrednostim argumenta, in ordinate - ustrezne vrednosti funkcij.

OSNOVNE LASTNOSTI FUNKCIJ

1. Funkcijske ničle

Nič funkcije je vrednost argumenta, pri kateri je vrednost funkcije enaka nič.

2. Intervali konstantnega predznaka funkcije

Intervali konstantnega znaka funkcije so nizi vrednosti argumentov, na katerih so vrednosti funkcije samo pozitivne ali samo negativne.

3. Naraščajoča (padajoča) funkcija.

Povečanje v nekem intervalu je funkcija funkcija, za katero višja vrednost argument iz tega intervala ustreza večji vrednosti funkcije.

funkcija y = f ( x ) klical povečevanje na intervalu (A; b ), če za kakšno x 1 in x 2 iz tega intervala tako, dax 1 < x 2 , neenakost je resf ( x 1 )< f ( x 2 ).

Sestopanje v določenem intervalu je funkcija tista funkcija, pri kateri večja vrednost argumenta iz tega intervala ustreza manjši vrednosti funkcije.

funkcija pri = f ( x ) klical zmanjševanje na intervalu (A; b ) , če sploh x 1 in x 2 iz tega intervala tako, da x 1 < x 2 , neenakost je resf ( x 1 )> f ( x 2 ).

4. Soda (liha) funkcija

Celotna funkcija - funkcija, katere domena definicije je simetrična glede na izvor in za katero koliX s področja definicije enakostf (- x ) = f ( x ) . Graf sode funkcije je simetričen glede na ordinato.

Na primer, y = x 2 - enakomerna funkcija.

Čudna funkcija- funkcija, katere domena definicije je simetrična glede na izvor in za katero koli X s področja definicije velja enakost f (- x ) = - f (x ). Graf lihe funkcije je simetričen glede na izvor.

Na primer: y = x 3 - čudna funkcija .

funkcija splošni pogled ni sodo ali liho (y = x 2 +x ).

Lastnosti nekaterih funkcij in njihove grafike

1. Linearna funkcija imenujemo funkcija oblike , Kje k in b – številke.

Definicijsko področje linearne funkcije je množicaR realna števila.

Graf linearne funkcijepri = kx + b ( k ≠ 0) je premica, ki poteka skozi točko (0;b ) in vzporedno s premicopri = kx .

Ravna, ne vzporedna z osjoOU, je graf linearne funkcije.

Lastnosti linearne funkcije.

1. Kdaj k > 0 funkcija pri = kx + b

2. Kdaj k < 0 funkcija y = kx + b zmanjševanje v domeni definicije.

l = kx + b ( k ≠ 0 ) je celotna številska premica, tj. kupR realna števila.

pri k = 0 niz funkcijskih vrednostiy = kx + b je sestavljen iz ene številkeb .

3. Kdaj b = 0 in k = 0 funkcija ni niti soda niti liha.

pri k = 0 linearna funkcija izgleda koty = b in pri b ≠ 0 enako je.

pri k = 0 in b = 0 linearna funkcija ima oblikoy = 0 in je hkrati sodo in liho.

Graf linearne funkcijey = b je premica, ki poteka skozi točko (0; b ) in vzporedno z osjoOh. Upoštevajte, da ko b = 0 funkcijski grafy = b sovpadajo z osjo Oh .

5. Kdaj k > 0 to imamo pri> 0 če in pri< 0 če. pri k < 0 imamo, da je y > 0 če in pri< 0, если .

2. Funkcija l = x 2

Rrealna števila.

Podajanje spremenljivkeX več vrednosti iz domene funkcije in izračun ustreznih vrednostipri po formuli l = x 2 , prikažemo graf funkcije.

Graf funkcije l = x 2 klical parabola.

Lastnosti funkcije y = x 2 .

1. Če X= 0, torej y = 0, tj. parabola ima koordinatne osi skupna točka(0; 0) - izvor.

2. Če x ≠ 0 , to pri > 0, tj. vse točke parabole, razen izhodišča, ležijo nad osjo x.

3. Množica funkcijskih vrednostipri = X 2 je funkcija razponapri = X 2 zmanjša.

X

3. Funkcija

Domena te funkcije je funkcija razponal = | x | zmanjša.

7. Najnižja vrednost funkcija prevzame na točkiX, to je enako 0. Največja vrednost ne obstaja.

6. funkcija

Obseg funkcije: .

Obseg funkcij: .

Graf je hiperbola.

1. Funkcijske ničle.

y ≠ 0, brez ničel.

2. Intervali konstantnosti znakov,

če k > 0, torej pri> 0 pri X > 0; pri < 0 при X < О.

če k < 0, то pri < 0 при X > 0; pri> 0 pri X < 0.

3. Intervali povečanja in zmanjšanja.

če k > 0, potem funkcija pada kot .

če k < 0, то функция возрастает при .

4. Soda (liha) funkcija.

Funkcija je čudna.

Kvadratni trinom

Enačba oblike sekira 2 + bx + c = 0, kjer je a , b in z - nekaj številk ina≠ 0, klicano kvadrat.

V kvadratni enačbisekira 2 + bx + c = 0 koeficient A klical prvi koeficient b - drugi koeficienti, z - brezplačen član.

Korenska formula kvadratna enačba ima obliko:

.

Izraz se imenuje diskriminator kvadratna enačba in je označena zD .

če D = 0, potem enačba izpolnjuje samo eno število sekira 2 + bx + c = 0. Vendar smo se dogovorili, da ima kvadratna enačba v tem primeru dva enaka realna korena in število samo klical dvojni koren.

če D < 0, то квадратное уравнение не имеет действительных корней.

če D > 0, potem ima kvadratna enačba dve različni prave korenine.

Naj bo podana kvadratna enačbasekira 2 + bx + c = 0. Ker a≠ 0, nato pa oba dela razdelite podana enačba naA, dobimo enačbo . Verjeti in , pridemo do enačbe , pri kateri je prvi koeficient enak 1. Ta enačba se imenujedano.

Formula za korenine zgornje kvadratne enačbe je:

.

Enačbe oblike

A x 2 + bx = 0, sekira 2 + s = 0, A x 2 = 0

se imenujejo nepopolne kvadratne enačbe. Nepopolne kvadratne enačbe se rešujejo z faktorizacijo leve strani enačbe.

Vietov izrek .

Vsota korenin kvadratne enačbe je enaka razmerju med drugim koeficientom in prvim, vzetim z nasprotnim predznakom, produkt korenin pa je razmerje med prostim členom in prvim koeficientom, tj.

Konverzni izrek.

Če je vsota katerih koli dveh številX 1 in X 2 enako , njun produkt pa je enak, potem so te številke korenine kvadratne enačbeOh 2 + b x + c = 0.

Funkcija obrazca Oh 2 + b x + c klical kvadratni trinom. Koreni te funkcije so koreni ustrezne kvadratne enačbeOh 2 + b x + c = 0.

Če je diskriminant kvadratni trinom večji od nič, potem lahko ta trinom predstavimo kot:

Oh 2 + b x + c = a(x-x 1 )(x-x 2 )

Kje X 1 in X 2 - korenine trinoma

Če je diskriminant kvadratnega trinoma enako nič, potem lahko ta trinom predstavimo kot:

Oh 2 + b x + c = a(x-x 1 ) 2

Kje X 1 - koren trinoma.

na primer 3x 2 - 12x + 12 = 3(x - 2) 2 .

Enačba oblike Oh 4 + b X 2 + s= 0 se kliče bikvadraten. Uporaba zamenjave spremenljivke s formuloX 2 = l reducira se na kvadratno enačboA l 2 + avtor + c = 0.

Kvadratna funkcija

Kvadratna funkcija je funkcija, ki jo lahko zapišemo s formulo oblikel = sekira 2 + bx + c , Kje x - neodvisna spremenljivka,a , b in c – nekaj številk ina ≠ 0.

Lastnosti funkcije in vrsta njenega grafa so določene predvsem z vrednostmi koeficientaa in diskriminator.

Lastnosti kvadratne funkcije

Domena:R;

Razpon vrednosti:

pri A > 0 [- D/(4 a); ∞)

pri A < 0 (-∞; - D/(4 a)];

Sodo liho:

pri b = 0 soda funkcija

pri b ≠ Funkcija 0 ni niti soda niti liha

pri D> 0 dve ničli: ,

pri D= 0 ena ničla:

pri D < 0 нулей нет

Intervali konstantnosti predznaka:

če je a > 0, D> 0, torej

če je a > 0, D= 0, torej

eče je a > 0, D < 0, то

če< 0, D> 0, torej

če< 0, D= 0, torej

če< 0, D < 0, то

- Intervali monotonije

za a > 0

pri a< 0

Graf kvadratne funkcije jeparabola – krivulja, ki je simetrična glede na ravno črto , ki poteka skozi oglišče parabole (oglišče parabole je točka presečišča parabole s simetrijsko osjo).

Za graf kvadratne funkcije potrebujete:

1) poiščite koordinate vrha parabole in jo označite v koordinatni ravnini;

2) zgradite več točk, ki pripadajo paraboli;

3) povežite označene točke z gladko črto.

Koordinate vrha parabole so določene s formulami:

; .

Pretvarjanje grafov funkcij

1. Raztezanje grafične umetnostiy = x 2 vzdolž osipri V|a| krat (ob|a| < 1 je stiskanje 1/|a| enkrat).

Če in< 0, произвести, кроме того, zrcalni odsev grafika o osiX (veje parabole bodo usmerjene navzdol).

rezultat: graf funkcijey = ah 2 .

2. Vzporedni prenos funkcijska grafikay = ah 2 vzdolž osiX na| m | (na desno, ko

m > 0 in v levo koT< 0).

Rezultat: graf funkcijey = a(x - t) 2 .

3. Vzporedni prenos funkcijska grafika vzdolž osipri na| n | (gor obp> 0 in navzdol prip< 0).

Rezultat: graf funkcijey = a(x - t) 2 + str.

Kvadratne neenakosti

Neenakosti oblikeOh 2 + b x + c > 0 inOh 2 + bx + c< 0, kjeX - spremenljivka,a , b inz - nekaj številk ina≠ 0 imenujemo neenakosti druge stopnje z eno spremenljivko.

Reševanje neenakosti druge stopnje v eni spremenljivki si lahko predstavljamo kot iskanje intervalov, v katerih ima ustrezna kvadratna funkcija pozitivne ali negativne vrednosti.

Za reševanje neenačb oblikeOh 2 + bx + c > 0 inOh 2 + bx + c< 0 nadaljujte na naslednji način:

1) poiščite diskriminant kvadratnega trinoma in ugotovite, ali ima trinom korenine;

2) če ima trinom korenine, jih označite na osiX in skozi označene točke je shematsko narisana parabola, katere veje so usmerjene navzgorA > 0 ali navzdol, koA< 0; če trinom nima korenin, potem shematično upodabljajte parabolo, ki se nahaja v zgornji polravnini priA > 0 ali nižje priA < 0;

3) najdemo na osiX intervali, pri katerih se točke parabole nahajajo nad osjoX (če je neenakost rešenaOh 2 + bx + c > 0) ali pod osjoX (če je neenakost rešenaOh 2 + bx + c < 0).

primer:

Rešimo neenačbo .

Upoštevajte funkcijo

Njegov graf je parabola, katere veje so usmerjene navzdol (od ).

Ugotovimo, kako se graf nahaja glede na osX. Rešimo enačbo za to . To razumemox = 4. Enačba ima en sam koren. To pomeni, da se parabola dotika osiX.

S shematskim prikazom parabole ugotovimo, da ima funkcija negativne vrednosti za katero koliX, razen 4.

Odgovor lahko zapišemo takole:X - poljubno število, ki ni enako 4.

Reševanje neenačb z intervalno metodo

diagram rešitve

1. Poiščite ničle funkcijo na levi strani neenakosti.

2. Označi položaj ničel na številski osi in določi njihovo množino (Ček jaz je sodo, potem je nič sode mnogokratnosti, ček jaz liho je liho).

3. Poiščite znake funkcije v intervalih med njenimi ničlami, začenši od skrajno desnega intervala: v tem intervalu je funkcija na levi strani neenakosti vedno pozitivna za dano obliko neenačb. Pri prehodu od desne proti levi skozi ničlo funkcije iz enega intervala v sosednji je treba upoštevati:

če je nič liho večkratnost, predznak funkcije se spremeni,

če je nič soda večkratnosti, se predznak funkcije ohrani.

4. Zapiši odgovor.

primer:

(x + 6) (x + 1) (X - 4) < 0.

Najdene ničle funkcij. Enakopravni so:X 1 = -6; X 2 = -1; X 3 = 4.

Na koordinatni premici označimo ničle funkcijef ( x ) = (x + 6) (x + 1) (X - 4).

Poiščimo predznake te funkcije v vsakem od intervalov (-∞; -6), (-6; -1), (-1; 4) in

Iz slike je razvidno, da je množica rešitev neenačbe unija intervalov (-∞; -6) in (-1; 4).

Odgovor: (-∞ ; -6) in (-1; 4).

Obravnavana metoda za reševanje neenačb se imenujeintervalna metoda.

Domena definicije in območje vrednosti funkcije. IN elementarna matematika funkcije preučujemo samo na množici realnih števil R.To pomeni, da lahko argument funkcije sprejme samo tiste realne vrednosti, za katere je funkcija definirana, tj. sprejema tudi samo prave vrednote. Kup X vse velja prave vrednosti prepir x, za katerega funkcija l= f(x)določen, imenovan domena funkcije. Kup Y vse prave vrednosti l, ki ga funkcija sprejme, se imenuje obseg delovanja. Zdaj lahko daš več natančna definicija Lastnosti: pravilo(zakon) korespondence med množicama X in Y, po kateri za vsak element iz množiceX lahko najde en in samo en element iz množice Y, ki se imenuje funkcija.

Iz te definicije sledi, da se funkcija šteje za definirano, če:

Domena funkcije je določena X ;

Funkcijsko območje je določeno Y ;

Znano je pravilo (zakon) dopisovanja in to tako, da za vsak

Za vrednost argumenta je mogoče najti samo eno vrednost funkcije.

Ta zahteva po edinstvenosti funkcije je obvezna.

Monotona funkcija.Če za kateri koli dve vrednosti argumenta x 1 in x 2 pogoja x 2 > x 1 sledi f(x 2) > f(x 1), nato funkcijo f(x) je poklican povečevanje; če za kakšno x 1 in x 2 pogoja x 2 > x 1 sledi f(x 2) < f(x 1), nato funkcijo f(x) je poklican zmanjševanje. Pokličemo funkcijo, ki samo narašča ali samo pada monotono.

Omejene in neomejene funkcije. Funkcija se imenuje omejeno, če kaj takega obstaja pozitivno število M kaj | f(x) | M za vse vrednosti x.Če taka številka ne obstaja, potem funkcija obstaja neomejeno.

PRIMERI.

Funkcija, prikazana na sliki 3, je omejena, vendar ni monotona. Funkcija na sliki 4 je ravno nasprotna, monotona, a neomejena. (Prosim, razložite to!).

Kontinuirane in diskontinuirane funkcije. funkcija l = f (x) je poklican neprekinjeno na točkix = a, Če:

1) funkcija je definirana, ko x = a, tj. f (a) obstaja;

2) obstaja končno limit lim f (x) ;

x→a

(glejte Omejitve funkcij)

3) f (a) = lim f (x) .

x→a

Če vsaj eden od teh pogojev ni izpolnjen, se funkcija pokliče eksplozivno na točki x = a.

Če je funkcija med vsi točke njene definicijske domene, potem se imenuje neprekinjena funkcija.

Sode in lihe funkcije.Če za kaj x f(- x) = f (x), nato se funkcija pokliče celo;če se pojavi: f(- x) = - f (x), nato se funkcija pokliče Čuden. Graf sode funkcije simetrično glede na os Y(slika 5), ​​graf lihe funkcije Simmetrika glede na izvor(slika 6).

Periodična funkcija. funkcija f (x) - periodično, če kaj takega obstaja različen od ničštevilo T kaj za kaj x iz domene definicije funkcije velja: f (x + T) = f (x). to vsajštevilka se kliče obdobje funkcije. Vse trigonometrične funkcije so periodični.

Primer 1. Dokaži ta greh x ima obdobje 2.

Rešitev: Vemo, da greh ( x+ 2n) = greh x, Kje n= 0, ± 1, ± 2, …

Torej dodatek 2 n ne na sinusni argument

Spreminja svoj pomen. Ali obstaja še ena številka s tem

Ista lastnina?

Pretvarjajmo se, da p- takšno število, tj. enakost:

greh( x+ P) = greh x,

Velja za katero koli vrednost x. Ampak potem je

Kraj in čas x= / 2, tj.

Greh (/2 + p) = greh / 2 = 1.

Toda glede na redukcijsko formulo sin ( / 2 + p) = cos p. Potem

Iz zadnjih dveh enakosti sledi, da je cos p= 1, ampak mi

Vemo, da je to res samo takrat, ko p = 2n. Od najmanjšega

Število, ki ni nič od 2 n je 2, potem je to število

In obstaja menstrualni greh x. Na podoben način je mogoče dokazati, da 2 od n je , torej je to obdobje sin 2 x.

Funkcijske ničle. Pokliče se vrednost argumenta, pri kateri je funkcija enaka 0 nič (root) funkcijo. Funkcija ima lahko več ničel. Na primer funkcija l = x (x + 1) (x-3) ima tri ničle: x= 0, x= -1, x= 3. Geometrično ničelna funkcija - to je abscisa točke presečišča grafa funkcije z osjo X .

Slika 7 prikazuje graf funkcije z ničlami: x= a, x = b in x= c.

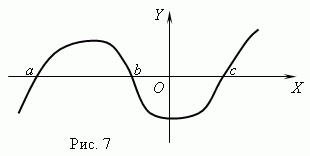
Asimptota.Če se graf funkcije neomejeno približuje določeni premici, ko se odmika od izhodišča, se ta premica imenuje asimptota.

Opredelitev: Numerična funkcija je korespondenca, ki povezuje vsako število x iz danega niza ednina l.

Oznaka:

kjer je x neodvisna spremenljivka (argument), y je odvisna spremenljivka (funkcija). Niz vrednosti x se imenuje domena funkcije (označeno z D(f)). Niz vrednosti y se imenuje obseg vrednosti funkcije (označeno z E(f)). Graf funkcije je množica točk v ravnini s koordinatami (x, f(x))

Metode za določanje funkcije.

1. analitična metoda (z uporabo matematične formule);
2. tabelarična metoda (z uporabo tabele);
3. deskriptivna metoda (uporaba besednega opisa);
4. grafična metoda (z uporabo grafa).

Osnovne lastnosti funkcije.

1. Sodo in liho

Funkcija se pokliče tudi, če
– domena definicije funkcije je simetrična glede na nič
f(-x) = f(x)

Graf sode funkcije je simetričen glede na os 0y

Funkcija se imenuje liho, če
– domena definicije funkcije je simetrična glede na nič
– za vsak x iz domene definicije f(-x) = –f(x)

Urnik nenavadna funkcija simetričen glede izvora.

2. Pogostost

Funkcijo f(x) imenujemo periodična s periodo if za vsak x iz domene definicije f(x) = f(x+T) = f(x-T) .

Urnik periodična funkcija sestoji iz neomejeno ponavljajočih se enakih fragmentov.

3. Monotonost (naraščajoča, padajoča)

Funkcija f(x) narašča na množici P, če je za kateri koli x 1 in x 2 iz te množice tako, da je x 1

Funkcija f(x) pada na množici P, če je za katerikoli x 1 in x 2 iz te množice tako, da je x 1 f(x 2) .

4. Ekstremi

Točka X max se imenuje največja točka funkcije f(x), če je za vse x iz neke okolice X max izpolnjena neenakost f(x) f(X max).

Vrednost Y max =f(X max) se imenuje maksimum te funkcije.

X max – največja točka
Pri max - maksimalno

Točka X min se imenuje točka minimuma funkcije f(x), če je za vse x iz neke okolice X min izpolnjena neenakost f(x) f(X min).

Vrednost Y min =f(X min) imenujemo minimum te funkcije.

X min – najmanjša točka
Y min – minimum

X min , X max – ekstremne točke
Y min , Y max – ekstremi.

5. Ničle funkcije

Nič funkcije y = f(x) je vrednost argumenta x, pri kateri funkcija postane nič: f(x) = 0.

X 1, X 2, X 3 – ničle funkcije y = f(x).

Naloge in testi na temo "Osnovne lastnosti funkcije"

• Lastnosti funkcije - Numerične funkcije 9. razred

  Lekcije: 2 Naloge: 11 Testi: 1

• Lastnosti logaritmov - Eksponentne in logaritemske funkcije 11. razred

  Lekcije: 2 Naloge: 14 Testov: 1

• Funkcija kvadratnega korena, njene lastnosti in graf - Funkcija kvadratni koren. Lastnosti kvadratnega korena stopnje 8

  Lekcije: 1 Naloge: 9 Testi: 1

• Potenčne funkcije, njihove lastnosti in grafi - Stopinje in koreni. Potenčne funkcije 11. razred

  Lekcije: 4 Naloge: 14 Testi: 1

• Funkcije - Pomembne teme Za ponavljanje enotnega državnega izpita matematika

  Naloge: 24

Po študiju te teme bi morali biti sposobni najti domeno definicije različne funkcije, določanje intervalov monotonosti funkcije z uporabo grafov, preverjanje sodosti in lihosti funkcij. Razmislimo o rešitvi podobne naloge z uporabo naslednjih primerov.

Primeri.

1. Poiščite domeno definicije funkcije.

rešitev: domeno definicije funkcije najdemo iz pogoja

Da bi razumeli to temo, razmislimo o funkciji, prikazani na grafu // Pokažimo, kako graf funkcije omogoča določanje njenih lastnosti.

Oglejmo si lastnosti funkcije na primeru

Domena definicije funkcije je razpon [ 3,5; 5.5].

Območje vrednosti funkcije je razpon [ 1; 3].

1. Pri x = -3, x = - 1, x = 1,5, x = 4,5 je vrednost funkcije enaka nič.

Vrednost argumenta, pri kateri je vrednost funkcije nič, se imenuje funkcija nič.

// tiste. za to funkcijo so števila -3;-1;1,5; 4,5 so ničle.

2. V intervalih [ 4,5; 3) in (1; 1.5) ter (4.5; 5.5] se graf funkcije f nahaja nad abscisno osjo, v intervalih (-3; -1) in (1.5; 4.5) pod abscisno osjo pa je razloženo takole - v intervalih[ 4,5; 3) in (1; 1,5) ter (4,5; 5,5] funkcija zavzema pozitivne vrednosti, na intervalih (-3; -1) in (1,5; 4,5) pa negativne vrednosti.

Vsak od navedenih intervalov (kjer funkcija zavzema vrednosti istega predznaka) se imenuje interval konstantnega predznaka funkcije f.//tj. če na primer vzamemo interval (0; 3), potem to ni interval konstantnega predznaka te funkcije.

V matematiki je pri iskanju intervalov konstantnega predznaka funkcije običajno navesti intervale največje dolžine. //Tiste. interval (2; 3) je interval konstantnosti predznaka funkcija f, vendar mora odgovor vsebovati interval [ 4.5; 3), ki vsebuje interval (2; 3).

3. Če se premaknete vzdolž osi x od 4,5 do 2, boste opazili, da gre graf funkcije navzdol, to je, da se vrednosti funkcije zmanjšajo. //V matematiki je običajno reči, da na intervalu [ 4.5; 2] funkcija pada.

Ko x narašča od 2 do 0, gre graf funkcije navzgor, tj. vrednosti funkcije se povečajo. //V matematiki je običajno reči, da na intervalu [ 2; 0] funkcija narašča.

Funkcija f je poklicana, če za kateri koli dve vrednosti argumenta x1 in x2 iz tega intervala, tako da je x2 > x1, velja neenakost f (x2) > f (x1). // ali je funkcija poklicana narašča v določenem intervalu, če za katero koli vrednost argumenta iz tega intervala večja vrednost argumenta ustreza večji vrednosti funkcije.//tj. več kot je x, več je y.

Pokliče se funkcija f zmanjševanje v določenem intervalu, če je za katerikoli dve vrednosti argumenta x1 in x2 iz tega intervala, tako da je x2 > x1, neenakost f(x2) padajoča na nekem intervalu, če je za katero koli vrednost argumenta iz tega intervala večja vrednost argumenta ustreza manjši vrednosti funkcije. // tiste. več kot je x, manj je y.

Če funkcija narašča po celotnem definiranem področju, se jo pokliče povečevanje.

Če funkcija pada v celotni definicijski domeni, jo pokličemo zmanjševanje.

Primer 1. graf naraščajočih oziroma padajočih funkcij.

Primer 2.

Opredelite pojav. Ali linearna funkcija f(x) = 3x + 5 narašča ali pada?

Dokaz. Uporabimo definicije. Naj sta x1 in x2 poljubni vrednosti argumenta in x1< x2., например х1=1, х2=7

Meje in kontinuiteta

Kompleti

Spodaj veliko razumemo kot zbirko homogenih predmetov. Predmeti, ki tvorijo množico, se imenujejo elementi oz pike te množice. Množice označujejo z velikimi tiskanimi črkami, njihovi elementi pa so male črke. če a je element nabora A, potem se uporabi vnos aÎ A. če b ni element nabora A, potem je zapisano takole: b Ï A. Množica, ki ne vsebuje niti enega elementa, se imenuje prazna množica in jo označimo na naslednji način: Ø.

Če nastavite B sestavljen iz dela elementov sklopa A ali sovpada z njim, potem niz B klical podnabor množice in označujejo BÌ A.

Dva sklopa se imenujeta enaka, če so sestavljeni iz istih elementov.

Združenje dva kompleta A in B imenovan niz C, sestavljen iz vseh elementov, ki pripadajo vsaj enemu od nizov: C=AÈ B.

S prečkanjem dva kompleta A in B imenovan niz C, sestavljen iz vseh elementov, ki pripadajo vsakemu od teh nizov: C=AÇ B.

Z razliko kompleti A in B imenovan niz E A, ki ne sodijo v sklop B: .

Dodatek kompleti AÌ B imenovan niz C, sestavljen iz vseh elementov nabora B, ne pripada A.

Množice, katerih elementi so realna števila, se imenujejo številčno:

pri čemer nÌ ZÌ QÌ R, jazÌ R in R=jazÈ Q.

Kup X, katerega elementi izpolnjujejo neenakost, se imenuje segment(segment) in je označen z [ a; b]; neenakost a<x<b – interval in je označen z (); neenakosti in - polovični intervali in sta označena z oz. Pogosto se morate ukvarjati tudi z neskončnimi intervali in polintervali: , , in . Primerno jih je poklicati vse v intervalih .

Interval, tj. množica točk, ki izpolnjujejo neenakost (kjer ), se imenuje -okolica točke a.

Pojem funkcije. Osnovne lastnosti funkcije

Če vsak element x kompleti X se ujema en sam element l kompleti Y, potem pravijo, da na snemanju X dano funkcijo l=f(x). pri čemer x klical neodvisna spremenljivka oz prepir, A l – odvisna spremenljivka oz funkcijo, A f označuje zakon korespondence. Kup X klical domena definicije funkcije in niz Y – obseg vrednosti funkcije.

Obstaja več načinov za določanje funkcij.

1) Analitična metoda - funkcija je podana s formulo oblike l=f(x).

2) Tabelarna metoda - funkcija je določena s tabelo, ki vsebuje vrednosti argumentov in ustrezne vrednosti funkcije l=f(x).

3) Grafična metoda - upodobitev grafa funkcije, tj. niz točk ( x; l) koordinatna ravnina, katerih abscise predstavljajo vrednosti argumenta, ordinate pa ustrezne vrednosti funkcije l=f(x).

4) Verbalna metoda - funkcija je opisana s pravilom za njeno sestavo. Na primer, Dirichletova funkcija ima vrednost 1, če x je racionalno število in 0, če x– iracionalno število.

Razlikujemo naslednje glavne lastnosti funkcij.

1 Sodo in liho funkcija l=f(x) je poklican celo, če za katere koli vrednosti x iz svoje domene definicije je izpolnjen f(–x)=f(x), In Čuden, Če f(–x)=–f(x). Če nobena od naštetih enakosti ni izpolnjena, potem l=f(x) je poklican splošna funkcija. Graf sode funkcije je simetričen glede na os Oj, graf lihe funkcije pa je simetričen glede na izvor.

2 Monotonija funkcija l=f(x) je poklican povečevanje (zmanjševanje) na intervalu X, če večja vrednost argumenta iz tega intervala ustreza večji (manjši) vrednosti funkcije. Pustiti x 1 ,x 2 Î X, x 2 >x 1. Nato funkcija narašča na intervalu X, Če f(x 2)>f(x 1) in se zmanjša, če f(x 2)<f(x 1).

Poleg naraščajočih in padajočih funkcij se upoštevajo še nepadajoče in nenaraščajoče funkcije. Funkcija se imenuje nepadajoča (nenaraščajoča), če pri x 1 ,x 2 Î X, x 2 >x 1 velja neenakost f(x 2)≥f(x 1) (f(x 2)≤f(x 1)).

Naraščajoče in padajoče funkcije, pa tudi nenaraščujoče in nepadajoče funkcije imenujemo monotone.

3 Omejeno funkcija l=f(x) se imenuje omejen na interval X, če obstaja tako pozitivno število M>0, kaj | f(x)|≤M za kogarkoli xÎ X. IN drugače funkcija naj bi bila neomejena X.

4 Frekvenca funkcija l=f(x) imenujemo periodično s periodo T≠0, če sploh x iz domene funkcije f(x+T)=f(x). V nadaljevanju s periodo razumemo najmanjšo pozitivno periodo funkcije.

Funkcija se imenuje eksplicitno, če je podana s formulo oblike l=f(x). Če je funkcija podana z enačbo F(x, l)=0, ni dovoljeno glede na odvisno spremenljivko l, potem se imenuje implicitno.

Pustiti l=f(x) je funkcija neodvisne spremenljivke, definirane na množici X z obsegom Y. Povežimo vsakega posebej lÎ Y en pomen xÎ X, pri katerem f(x)=l.Nato nastala funkcija x=φ (l), definirana na nizu Y z obsegom X, poklical vzvratno in je določen l=f –1 (x). Grafi medsebojno inverzne funkcije simetrična glede na simetralo prve in tretje koordinatne četrtine.

Naj funkcija l=f(u) je funkcija spremenljivke u, definiran na nizu U z obsegom Y, in spremenljivko u v zameno je funkcija u=φ (x), definirana na nizu X z obsegom U. Nato podano na snemanju X funkcijo l=f(φ (x)) je poklican kompleksna funkcija (sestava funkcij, superpozicija funkcij, funkcija funkcije).

Elementarne funkcije

Glavne osnovne funkcije vključujejo:

• funkcija moči l=x n; l=x–n in l=x 1/ n;
• eksponentna funkcija l=a x;
• logaritemska funkcija l=log a x;
• trigonometrične funkcije l= greh x, l=cos x, l=tg x in l=ctg x;
• inverzne trigonometrične funkcije l= arcsin x, l=arccos x, l=arctg x in l=arcctg x.

Od glavnih elementarne funkcije nove funkcije je mogoče pridobiti z uporabo algebraične operacije in superpozicija funkcij.

Funkcije, sestavljene iz osnovnih elementarnih funkcij z uporabo končnega števila algebrskih operacij in končnega števila superpozicijskih operacij, imenujemo osnovno.

Algebraic imenovana funkcija, v kateri se izvede argument končna številka algebraične operacije. Algebraične funkcije vključujejo:

· cela racionalna funkcija(polinom ali polinom)

· frakcijska racionalna funkcija(razmerje dveh polinomov)

· iracionalna funkcija(če operacije na argumentu vključujejo ekstrakcijo korena).

Vsaka nealgebraična funkcija se imenuje transcendentalno. Transcendentne funkcije vključujejo eksponentne, logaritemske, trigonometrične in inverzne trigonometrične funkcije.