Osnovna pravila za decimalke. Sestavljanje sistema enačb

Ta članek govori o decimalke . Tu bomo razumeli decimalni zapis ulomkov, predstavili pojem decimalni ulomek in podali primere decimalnih ulomkov. Nato bomo govorili o števkah decimalnih ulomkov in dali imena števk. Po tem se bomo osredotočili na neskončne decimalne ulomke, govorili bomo o periodičnih in neperiodičnih ulomkih. Nato naštejemo osnovne operacije z decimalnimi ulomki. Za konec ugotovimo položaj decimalnih ulomkov na koordinatni žarek.

Navigacija po straneh.

Decimalni zapis ulomkov

Branje decimalk

Povejmo nekaj besed o pravilih branja decimalnih ulomkov.

Decimalni ulomki, ki ustrezajo pravim navadnim ulomkom, se berejo na enak način kot ti navadni ulomki, le da se najprej doda »nič celo število«. Na primer, decimalni ulomek 0,12 ustreza navadni ulomek 12/100 (beri "dvanajst stotink"), torej se 0,12 glasi "nič pika dvanajst stotink".

Decimalni ulomki, ki ustrezajo mešanim številom, se berejo popolnoma enako kot ta mešana števila. Na primer, decimalni ulomek 56,002 ustreza mešano število, zato se decimalni ulomek 56,002 bere kot "šestinpetdeset in dve tisočinki."

Mesta v decimalkah

Pri pisanju decimalnih ulomkov, pa tudi pri pisanju naravna števila, je pomen vsake števke odvisen od njenega položaja. Dejansko številka 3 v decimalnem ulomku 0,3 pomeni tri desetinke, v decimalnem ulomku 0,0003 - tri desettisočinke, v decimalnem ulomku 30.000,152 pa tri desettisočinke. Torej lahko govorimo o decimalnih mest, pa tudi o cifrah v naravnih številih.

Imena decimalnih mest do decimalno vejico popolnoma sovpadajo z imeni števk v naravnih številih. In imena decimalnih mest za decimalno vejico so razvidna iz naslednje tabele.

Na primer, v decimalnem ulomku 37.051 je številka 3 na mestu desetin, 7 na mestu enot, 0 je na mestu desetin, 5 je na mestu stotink in 1 je na mestu tisočink.

Mesta v decimalnih ulomkih se razlikujejo tudi po prednosti. Če se pri pisanju decimalnega ulomka premikamo od števke do števke od leve proti desni, potem se bomo premikali od starejši Za mlajših činov. Na primer, mesto stotin je starejše od mesta desetin, mesto milijonov pa nižje od mesta stotink. V danem končnem decimalnem ulomku lahko govorimo o velikih in stranskih cifrah. Na primer, v decimalnem ulomku 604,9387 višji (najvišji) mesto je mesto stotin in mlajši (najnižji)- desettisočinka.

Pri decimalnih ulomkih pride do razširitve v števke. Podobno je razširjanju naravnih števil v števke. Na primer, razširitev v decimalna mesta 45,6072 je naslednja: 45,6072=40+5+0,6+0,007+0,0002. In lastnosti seštevanja iz razgradnje decimalnega ulomka na števke vam omogočajo, da se premaknete na druge predstavitve tega decimalnega ulomka, na primer 45,6072=45+0,6072 ali 45,6072=40,6+5,007+0,0002 ali 45,6072= 45,0072+ 0,6.

Končne decimalke

Do sedaj smo govorili le o decimalnih ulomkih, v zapisu katerih za decimalno vejico stoji končna številkaštevilke Takšni ulomki se imenujejo končne decimalke.

Opredelitev.

Končne decimalke- To so decimalni ulomki, katerih zapisi vsebujejo končno število znakov (števk).

Tu je nekaj primerov končnih decimalnih ulomkov: 0,317, 3,5, 51,1020304958, 230 032,45.

Vendar ni mogoče vsakega ulomka predstaviti kot končno decimalko. Na primer, ulomka 5/13 ni mogoče nadomestiti z enakim ulomkom z enim od imenovalcev 10, 100, ..., zato ga ni mogoče pretvoriti v končni decimalni ulomek. O tem bomo več govorili v teoretičnem delu, pri pretvorbi navadnih ulomkov v decimalke.

Neskončne decimalke: periodični ulomki in neperiodični ulomki

Pri pisanju decimalnega ulomka za decimalno vejico lahko domnevate možnost neskončnega števila števk. V tem primeru bomo prišli do tako imenovanih neskončnih decimalnih ulomkov.

Opredelitev.

Neskončne decimalke- to so decimalni ulomki, katerih zapis vsebuje neskončen nizštevilke

Jasno je, da neskončnih decimalnih ulomkov ne moremo zapisati v polni obliki, zato se pri njihovem zapisu omejimo le na določeno končno število števk za decimalno vejico in postavimo elipso, ki označuje neskončno dolgo zaporedje števk. Tu je nekaj primerov neskončnih decimalnih ulomkov: 0,143940932…, 3,1415935432…, 153,02003004005…, 2,111111111…, 69,74152152152….

Če pozorno pogledate zadnja dva neskončna decimalna ulomka, potem je v ulomku 2,111111111... jasno vidna neskončno ponavljajoča se številka 1, v ulomku 69,74152152152..., začenši s tretjim decimalnim mestom, pa ponavljajoča se skupina števil 1, 5 in 2 je jasno vidna. Takšni neskončni decimalni ulomki se imenujejo periodični.

Opredelitev.

Periodične decimalke(ali samo periodični ulomki) so neskončni decimalni ulomki, pri zapisu katerih se, začenši z določenega decimalnega mesta, neskončno ponavlja neko število ali skupina števil, kar imenujemo obdobje ulomka.

Na primer, perioda periodičnega ulomka 2,111111111... je števka 1, perioda ulomka 69,74152152152... pa je skupina števk oblike 152.

Za neskončne periodične decimalne ulomke je sprejeto posebno obliko zapisi. Zaradi kratkosti smo se dogovorili, da piko zapišemo enkrat in jo damo v oklepaj. Na primer, periodični ulomek 2,111111111... je zapisan kot 2,(1) , periodični ulomek 69,74152152152... pa kot 69,74(152) .

Treba je omeniti, da je za isti periodični decimalni ulomek mogoče določiti različne periode. Na primer, periodični decimalni ulomek 0,73333... lahko obravnavamo kot ulomek 0,7(3) s periodo 3 in tudi kot ulomek 0,7(33) s periodo 33 in tako naprej 0,7(333), 0,7 (3333), ... Lahko pogledate tudi periodični ulomek 0,73333 ... takole: 0,733(3) ali takole 0,73(333) itd. Tu se, da bi se izognili dvoumnosti in neskladjem, strinjamo, da kot obdobje decimalnega ulomka štejemo najkrajše od vseh možnih zaporedij ponavljajočih se števk, začenši od najbližjega položaja do decimalne vejice. To pomeni, da bo obdobje decimalnega ulomka 0,73333... obravnavano kot zaporedje ene števke 3, periodičnost pa se začne od drugega mesta za decimalno vejico, to je 0,73333...=0,7(3). Drug primer: periodični ulomek 4,7412121212... ima periodo 12, periodičnost se začne od tretjega mesta za decimalno vejico, to je 4,7412121212...=4,74(12).

Neskončne decimalne periodične ulomke dobimo tako, da v decimalne ulomke pretvorimo navadne ulomke, katerih imenovalec vsebuje glavni dejavniki, drugačen od 2 in 5.

Tukaj velja omeniti periodične ulomke s periodo 9. Navedimo primere takih ulomkov: 6,43(9) , 27,(9) . Ti ulomki so še ena oznaka za periodične ulomke s periodo 0 in se običajno nadomestijo s periodičnimi ulomki s periodo 0. V ta namen se obdobje 9 nadomesti z obdobjem 0, vrednost naslednje najvišje števke pa se poveča za eno. Na primer, ulomek s periodo 9 v obliki 7,24(9) se nadomesti s periodičnim ulomkom s periodo 0 v obliki 7,25(0) ali enakim končnim decimalnim ulomkom 7,25. Drug primer: 4,(9)=5,(0)=5. Enakost ulomka s periodo 9 in njegovega ustreznega ulomka s periodo 0 zlahka ugotovimo, če te decimalne ulomke nadomestimo z enakimi navadnimi ulomki.

Za konec pa si poglejmo pobližje neskončne decimalne ulomke, ki ne vsebujejo neskončno ponavljajočega se zaporedja števk. Imenujejo se neperiodični.

Opredelitev.

Neponavljajoče se decimalke(ali samo neperiodični ulomki ) so neskončni decimalni ulomki brez obdobja.

Včasih imajo neperiodični ulomki podobno obliko kot periodični ulomki, na primer 8,02002000200002 ... je neperiodični ulomek. V teh primerih morate biti še posebej pozorni, da opazite razliko.

Upoštevajte, da se neperiodični ulomki ne pretvorijo v navadne ulomke; neskončni neperiodični decimalni ulomki predstavljajo iracionalna števila.

Operacije z decimalkami

Ena od operacij z decimalnimi ulomki je primerjanje, definirane pa so tudi štiri osnovne aritmetične funkcije operacije z decimalkami: seštevanje, odštevanje, množenje in deljenje. Razmislimo ločeno o vsakem dejanju z decimalnim ulomkom.

Primerjava decimalk v bistvu temelji na primerjavi navadnih ulomkov, ki ustrezajo primerjanim decimalnim ulomkom. Vendar pa je pretvorba decimalnih ulomkov v navadne ulomke precej delovno intenziven postopek in neskončnih neperiodičnih ulomkov ni mogoče predstaviti kot navaden ulomek, zato je priročno uporabiti primerjavo decimalnih ulomkov po mestu. Mestna primerjava decimalnih ulomkov je podobna primerjavi naravnih števil. Za podrobnejše informacije priporočamo, da preučite članek: primerjava decimalnih ulomkov, pravila, primeri, rešitve.

Pojdimo na naslednji korak - množenje decimalk. Množenje končnih decimalnih ulomkov poteka podobno kot odštevanje decimalnih ulomkov, pravila, primeri, rešitve množenja s stolpcem naravnih števil. Pri periodičnih ulomkih lahko množenje skrčimo na množenje navadnih ulomkov. Po drugi strani se množenje neskončnih neperiodičnih decimalnih ulomkov po njihovem zaokroževanju zmanjša na množenje končnih decimalnih ulomkov. Priporočamo nadaljnje preučevanje gradiva v članku: množenje decimalnih ulomkov, pravila, primeri, rešitve.

Decimale na koordinatnem žarku

Med točkami in decimalkami obstaja ujemanje ena proti ena.

Ugotovimo, kako so zgrajene točke na koordinatnem žarku, ki ustrezajo danemu decimalnemu ulomku.

Končne decimalne ulomke in neskončne periodične decimalne ulomke lahko nadomestimo z enakimi navadnimi ulomki in nato na koordinatnem žarku sestavimo ustrezne navadne ulomke. Na primer, decimalni ulomek 1,4 ustreza navadnemu ulomku 14/10, zato je točka s koordinato 1,4 odmaknjena od izhodišča v pozitivni smeri za 14 segmentov, ki so enaki desetini enotskega segmenta.

Decimalne ulomke lahko označimo na koordinatnem žarku, začenši z razgradnjo danega decimalnega ulomka na števke. Na primer, zgraditi moramo točko s koordinato 16.3007, ker je 16.3007=16+0.3+0.0007, potem v to točko tja lahko pridete tako, da od izvora zaporedno odložite 16 enotskih segmentov, 3 segmente, katerih dolžina je enaka desetinki enotskega segmenta, in 7 segmentov, katerih dolžina je enaka desettisočinki enotskega segmenta.

Ta način gradnje decimalna števila na koordinatnem žarku vam omogoča, da se kolikor želite približate točki, ki ustreza neskončnemu decimalnemu ulomku.

Včasih je mogoče natančno narisati točko, ki ustreza neskončnemu decimalnemu ulomku. na primer , potem ta neskončni decimalni ulomek 1,41421... ustreza točki na koordinatnem žarku, oddaljeni od izhodišča koordinat za dolžino diagonale kvadrata s stranico 1 enotskega segmenta.

Obratni postopek pridobivanja decimalnega ulomka, ki ustreza dani točki na koordinatnem žarku, je t.i. decimalno merjenje segmenta. Ugotovimo, kako se to naredi.

Naj bo naša naloga priti od izhodišča do določene točke na koordinatni premici (ali se ji neskončno približevati, če do nje ne moremo). Z decimalno meritvijo segmenta lahko zaporedno odložimo iz izhodišča poljubno število enotskih segmentov, nato segmente, katerih dolžina je enaka desetinki enote, nato segmente, katerih dolžina je enaka stotinki enote itd. Z zapisom števila segmentov vsake dolžine, odloženih na stran, dobimo decimalni ulomek, ki ustreza dani točki na koordinatnem žarku.

Na primer, da pridete do točke M na zgornji sliki, morate dati na stran 1 enotski segment in 4 segmente, katerih dolžina je enaka desetini enote. Tako točka M ustreza decimalnemu ulomku 1,4.

Jasno je, da točke koordinatnega žarka, ki jih v procesu decimalne meritve ni mogoče doseči, ustrezajo neskončnim decimalnim ulomkom.

Reference.

• Matematika: učbenik za 5. razred. splošno izobraževanje ustanove / N. Ya. Vilenkin, V. I. Zhokhov, A. S. Chesnokov, S. I. Shvartsburd. - 21. izd., izbrisano. - M.: Mnemosyne, 2007. - 280 str .: ilustr. ISBN 5-346-00699-0.
• Matematika. 6. razred: poučna. za splošno izobraževanje ustanove / [N. Ya. Vilenkin in drugi]. - 22. izd., rev. - M.: Mnemosyne, 2008. - 288 str.: ilustr. ISBN 978-5-346-00897-2.
• Algebra: učbenik za 8. razred. splošno izobraževanje institucije / [Yu. N. Makarychev, N. G. Mindyuk, K. I. Neshkov, S. B. Suvorova]; uredil S. A. Teljakovski. - 16. izd. - M .: Izobraževanje, 2008. - 271 str. : ill. - ISBN 978-5-09-019243-9.
• Gusev V.A., Mordkovič A.G. Matematika (priročnik za vpisnike v tehnične šole): Proc. dodatek.- M.; višje šola, 1984.-351 str., ilustr.

Zgodi se, da morate za udobje izračunov pretvoriti navaden ulomek v decimalno in obratno. O tem, kako to storiti, bomo govorili v tem članku. Oglejmo si pravila za pretvorbo navadnih ulomkov v decimalke in obratno ter navedimo primere.

Yandex.RTB R-A-339285-1

Razmislili bomo o pretvorbi navadnih ulomkov v decimalke po določenem zaporedju. Najprej poglejmo, kako navadne ulomke z imenovalcem, ki je večkratnik 10, pretvarjamo v decimalne: 10, 100, 1000 itd. Ulomki s takimi imenovalci so pravzaprav bolj okoren zapis decimalnih ulomkov.

Nato si bomo ogledali, kako navadne ulomke s poljubnim imenovalcem, ne le večkratnikom 10, pretvorimo v decimalne ulomke. Upoštevajte, da pri pretvorbi navadnih ulomkov v decimalne ulomke ne dobimo le končnih decimalnih ulomkov, temveč tudi neskončne periodične decimalne ulomke.

Pa začnimo!

Prevod navadnih ulomkov z imenovalci 10, 100, 1000 itd. na decimalke

Najprej povejmo, da nekateri ulomki zahtevajo nekaj priprav pred pretvorbo v decimalno obliko. kaj je Pred številom v števcu morate dodati toliko ničel, da bo število števk v števcu enako številu ničel v imenovalcu. Na primer, za ulomek 3100 je treba številko 0 enkrat dodati levo od številke 3 v števcu. Frakcija 610 v skladu z zgoraj navedenim pravilom ne potrebuje spremembe.

Poglejmo še en primer, po katerem bomo oblikovali pravilo, ki je na začetku še posebej priročno za uporabo, medtem ko ni veliko izkušenj s pretvorbo ulomkov. Torej bo ulomek 1610000 po dodajanju ničel v števcu videti kot 001510000.

Kako pretvoriti navadni ulomek z imenovalcem 10, 100, 1000 itd. na decimalno?

Pravilo za pretvorbo navadnih pravih ulomkov v decimalke

1. Zapišite 0 in za njo vstavite vejico.
2. Zapišemo število iz števca, ki smo ga dobili po seštevanju ničel.

Zdaj pa preidimo na primere.

Primer 1: Pretvarjanje ulomkov v decimalke

Pretvorimo ulomek 39.100 v decimalko.

Najprej pogledamo ulomek in vidimo, da jih ni pripravljalna dejanja tega ni treba storiti - število števk v števcu sovpada s številom ničel v imenovalcu.

Po pravilu zapišemo 0, za njo postavimo decimalno vejico in zapišemo število iz števca. Dobimo decimalni ulomek 0,39.

Poglejmo rešitev drugega primera na to temo.

Primer 2. Pretvarjanje ulomkov v decimalke

Zapišimo ulomek 105 10000000 kot decimalko.

Število ničel v imenovalcu je 7, števec pa ima samo tri števke. Pred številko v števcu dodamo še 4 ničle:

0000105 10000000

Sedaj zapišemo 0, za njo postavimo decimalno vejico in zapišemo število iz števca. Dobimo decimalni ulomek 0,0000105.

Ulomki, obravnavani v vseh primerih, so navadni pravilni ulomki. Toda kako pretvorite nepravilni ulomek v decimalno? Takoj povejmo, da priprava z dodajanjem ničel za takšne ulomke ni potrebna. Oblikujmo pravilo.

Pravilo za pretvorbo navadnih nepravilnih ulomkov v decimalke

1. Zapišite število, ki je v števcu.
2. Z decimalno vejico ločimo toliko števk na desni, kolikor ničel je v imenovalcu prvotnega ulomka.

Spodaj je primer uporabe tega pravila.

Primer 3. Pretvarjanje ulomkov v decimalke

Pretvorimo ulomek 56888038009 100000 iz navadnega nepravilnega ulomka v decimalni.

Najprej zapišimo število iz števca:

Zdaj na desni ločimo pet števk z decimalno vejico (število ničel v imenovalcu je pet). Dobimo:

Naslednje vprašanje, ki se seveda pojavi, je: kako pretvoriti mešano število v decimalni ulomek, če je imenovalec njegovega ulomka število 10, 100, 1000 itd. Če želite takšno število pretvoriti v decimalni ulomek, lahko uporabite naslednje pravilo.

Pravilo za pretvorbo mešanih števil v decimalke

1. Po potrebi pripravimo ulomek števila.
2. Prvotno številko zapišemo v celoti in za njo postavimo vejico.
3. Število iz števca ulomka zapišemo skupaj z dodanimi ničlami.

Poglejmo si primer.

Primer 4: Pretvarjanje mešanih števil v decimalke

Pretvorimo mešano število 23 17 10000 v decimalni ulomek.

V ulomku imamo izraz 17 10000. Pripravimo ga in dodamo še dve ničli levo od števca. Dobimo: 0017 10000.

Zdaj zapišemo cel del števila in za njim postavimo vejico: 23, . .

Za decimalno vejico zapišite število iz števca skupaj z ničlami. Dobimo rezultat:

23 17 10000 = 23 , 0017

Pretvarjanje navadnih ulomkov v končne in neskončne periodične ulomke

Seveda lahko pretvarjate v decimalke in navadne ulomke z imenovalcem, ki ni enak 10, 100, 1000 itd.

Pogosto lahko ulomek enostavno zmanjšamo na nov imenovalec in nato uporabimo pravilo iz prvega odstavka tega člena. Na primer, dovolj je, da števec in imenovalec ulomka 25 pomnožimo z 2 in dobimo ulomek 410, ki ga zlahka pretvorimo v decimalno obliko 0,4.

Vendar tega načina pretvorbe ulomka v decimalko ni mogoče vedno uporabiti. Spodaj bomo razmislili, kaj storiti, če obravnavane metode ni mogoče uporabiti.

Bistveno nov način za pretvorbo ulomka v decimalko je deljenje števca z imenovalcem s stolpcem. Ta operacija je zelo podobna deljenju naravnih števil s stolpcem, vendar ima svoje značilnosti.

Pri deljenju je števec predstavljen kot decimalni ulomek - desno od zadnje številke števca se postavi vejica in dodajo se ničle. V dobljenem količniku je decimalna vejica, ko se konča deljenje celega dela števca. Kako točno ta metoda deluje, bo jasno po ogledu primerov.

Primer 5. Pretvarjanje ulomkov v decimalke

Pretvorimo navadni ulomek 621 4 v decimalno obliko.

Predstavimo število 621 iz števca kot decimalni ulomek in za decimalno vejico dodamo nekaj ničel. 621 = 621,00

Zdaj pa razdelimo 621,00 s 4 z uporabo stolpca. Prvi trije koraki deljenja bodo enaki kot pri deljenju naravnih števil in dobili bomo.

Ko dosežemo decimalno vejico pri deljenem in je ostanek drugačen od nič, vstavimo decimalno vejico v količnik in nadaljujemo z deljenjem, pri čemer se ne oziramo več na vejico pri deljenem.

Kot rezultat dobimo decimalni ulomek 155, 25, ki je rezultat obračanja navadnega ulomka 621 4

621 4 = 155 , 25

Oglejmo si še en primer za okrepitev snovi.

Primer 6. Pretvarjanje ulomkov v decimalke

Obrnimo navadni ulomek 21 800.

Če želite to narediti, razdelite ulomek 21.000 v stolpec z 800. Deljenje celotnega dela se bo končalo na prvem koraku, zato takoj za njim v količnik vstavimo decimalno vejico in nadaljujemo z deljenjem, pri čemer se ne oziramo na vejico pri deljenem, dokler ne dobimo ostanka, ki je enak nič.

Kot rezultat smo dobili: 21.800 = 0,02625.

A kaj ko pri deljenju še vedno ne dobimo ostanka 0. V takšnih primerih lahko z deljenjem nadaljujemo v nedogled. Vendar pa se bodo ostanki občasno ponavljali od določenega koraka. V skladu s tem se bodo številke v količniku ponovile. To pomeni, da se navadni ulomek pretvori v decimalni neskončni periodični ulomek. Naj to ponazorimo s primerom.

Primer 7. Pretvarjanje ulomkov v decimalke

Pretvorimo navadni ulomek 19 44 v decimalko. Da bi to naredili, izvedemo delitev po stolpcu.

Vidimo, da se med deljenjem ponovita ostanka 8 in 36. V tem primeru se v količniku ponovita števili 1 in 8. To je obdobje v decimalnem ulomku. Pri snemanju so te številke v oklepajih.

Tako se prvotni navadni ulomek pretvori v neskončni periodični decimalni ulomek.

19 44 = 0 , 43 (18) .

Poglejmo nezmanjšani navadni ulomek. V kakšni obliki bo? Kateri navadni ulomki se pretvorijo v končne decimalke in kateri v neskončno periodične?

Najprej povejmo, da če je mogoče ulomek zmanjšati na enega od imenovalcev 10, 100, 1000..., potem bo imel obliko končnega decimalnega ulomka. Da se lahko ulomek skrči na enega od teh imenovalcev, mora biti njegov imenovalec delitelj vsaj enega od števil 10, 100, 1000 itd. Iz pravil za razlaganje števil na prafaktorje sledi, da je delitelj števil 10, 100, 1000 itd. mora, ko je faktoriziran na prafaktorje, vsebovati le števili 2 in 5.

Naj povzamemo povedano:

1. Navadni ulomek je mogoče zmanjšati na končno decimalko, če je njegov imenovalec mogoče faktorizirati na prafaktorja 2 in 5.
2. Če so poleg števil 2 in 5 v razširitvi imenovalca še druga števila praštevila, se ulomek reducira na obliko neskončnega periodičnega decimalnega ulomka.

Dajmo primer.

Primer 8. Pretvarjanje ulomkov v decimalke

Kateri od teh ulomkov 47 20, 7 12, 21 56, 31 17 se pretvori v končni decimalni ulomek in kateri le v periodičnega. Odgovorimo na to vprašanje, ne da bi neposredno pretvorili ulomek v decimalko.

Ulomek 47 20, kot je lahko videti, se z množenjem števca in imenovalca s 5 zmanjša na nov imenovalec 100.

47 20 = 235 100. Iz tega sklepamo, da se ta ulomek pretvori v končni decimalni ulomek.

Če razdelimo imenovalec ulomka 7 12 na faktorje, dobimo 12 = 2 · 2 · 3. Ker se prafaktor 3 razlikuje od 2 in 5, tega ulomka ni mogoče predstaviti kot končni decimalni ulomek, ampak bo imel obliko neskončnega periodičnega ulomka.

Najprej je treba zmanjšati ulomek 21 56. Po zmanjšanju za 7 dobimo nezmanjšani ulomek 3 8, katerega imenovalec faktoriziramo, da dobimo 8 = 2 · 2 · 2. Zato je končni decimalni ulomek.

V primeru ulomka 31 17 je imenovalec samo praštevilo 17. V skladu s tem lahko ta ulomek pretvorimo v neskončni periodični decimalni ulomek.

Navadnega ulomka ni mogoče pretvoriti v neskončni in neperiodični decimalni ulomek

Zgoraj smo govorili le o končnih in neskončnih periodičnih ulomkih. Toda ali je mogoče vsak navaden ulomek pretvoriti v neskončen neperiodični ulomek?

Odgovorimo: ne!

Pomembno!

Pri pretvorbi neskončnega ulomka v decimalko je rezultat končna decimalka ali neskončna periodična decimalka.

Ostanek delitve je vedno manj kot delitelj. Z drugimi besedami, po izreku o deljivosti, če neko naravno število delimo s številom q, ostanek pri deljenju v nobenem primeru ne more biti večji od q-1. Po končani delitvi je možna ena od naslednjih situacij:

1. Dobimo ostanek 0 in tu se deljenje konča.
2. Dobimo ostanek, ki se pri naslednjem deljenju ponovi, rezultat pa je neskončni periodični ulomek.

Pri pretvorbi ulomka v decimalko ne more biti drugih možnosti. Povejmo še, da je dolžina periode (število števk) v neskončnem periodičnem ulomku vedno manjša od števila števk v imenovalcu ustreznega navadnega ulomka.

Pretvarjanje decimalnih mest v ulomke

Zdaj je čas, da pogledamo obratni postopek pretvorbe decimalnega ulomka v navadni ulomek. Oblikujmo pravilo prevajanja, ki vključuje tri stopnje. Kako pretvoriti decimalni ulomek v navadni ulomek?

Pravilo za pretvorbo decimalnih ulomkov v navadne ulomke

1. V števec zapišemo število iz prvotnega decimalnega ulomka, pri čemer zavržemo vejico in vse ničle na levi, če so.
2. V imenovalec zapišemo ena in ji sledi toliko ničel, kolikor je števk za decimalno vejico v prvotnem decimalnem ulomku.
3. Po potrebi zmanjšajte nastalo navadno frakcijo.

Oglejmo si uporabo tega pravila na primerih.

Primer 8. Pretvarjanje decimalnih ulomkov v navadne ulomke

Predstavljajmo si število 3,025 kot navaden ulomek.

1. Sam decimalni ulomek zapišemo v števec, vejico pa zavržemo: 3025.
2. V imenovalec zapišemo eno, za njo pa tri ničle - točno toliko števk vsebuje prvotni ulomek za decimalno vejico: 3025 1000.
3. Dobljeni ulomek 3025 1000 lahko zmanjšamo za 25, rezultat pa je: 3025 1000 = 121 40.

Primer 9. Pretvarjanje decimalnih ulomkov v navadne ulomke

Pretvorimo ulomek 0,0017 iz decimalne v navadno.

1. V števec zapišemo ulomek 0, 0017, pri čemer zavržemo vejice in ničle na levi strani. Izkazalo se bo 17.
2. V imenovalec zapišemo ena, za njo pa štiri ničle: 17 10000. Ta ulomek je nezmanjšljiv.

Če ima decimalni ulomek cel del, potem lahko tak ulomek takoj pretvorimo v mešano število. Kako to narediti?

Oblikujmo še eno pravilo.

Pravilo za pretvorbo decimalk v mešana števila.

1. Število pred decimalno vejico v ulomku zapišemo kot celo število mešanega števila.
2. V števec zapišemo število za decimalno vejico v ulomku, ničle na levi strani, če so, zavržemo.
3. V imenovalec ulomka dodamo eno in toliko ničel, kolikor je števk za decimalno vejico v ulomku.

Vzemimo primer

Primer 10. Pretvarjanje decimalke v mešano število

Predstavljajmo si ulomek 155, 06005 kot mešano število.

1. Število 155 zapišemo kot celo število.
2. V števcu zapisujemo števila za decimalno vejico, ničlo zavržemo.
3. V imenovalec zapišemo ena in pet ničel

Naučimo se mešano število: 155 6005 100000

Ulomek lahko zmanjšamo za 5. Skrajšamo ga in dobimo končni rezultat:

155 , 06005 = 155 1201 20000

Pretvarjanje neskončnih periodičnih decimalnih mest v ulomke

Oglejmo si primere, kako periodične decimalne ulomke pretvoriti v navadne ulomke. Preden začnemo, pojasnimo: vsak periodični decimalni ulomek je mogoče pretvoriti v navaden ulomek.

Najenostavnejši primer je frakcijska doba enako nič. Periodični ulomek z ničelno periodo se nadomesti s končnim decimalnim ulomkom, postopek obračanja takega ulomka pa se zmanjša na obračanje končnega decimalnega ulomka.

Primer 11. Pretvarjanje periodičnega decimalnega ulomka v navadni ulomek

Obrnimo periodični ulomek 3, 75 (0).

Če odstranimo ničle na desni, dobimo končni decimalni ulomek 3,75.

Obračanje dani ulomek v običajno z uporabo algoritma, obravnavanega v prejšnjih odstavkih, dobimo:

3 , 75 (0) = 3 , 75 = 375 100 = 15 4 .

Kaj pa, če je perioda ulomka drugačna od nič? Periodični del je treba obravnavati kot vsoto členov geometrijskega napredovanja, ki pada. Razložimo to s primerom:

0 , (74) = 0 , 74 + 0 , 0074 + 0 , 000074 + 0 , 00000074 + . .

Obstaja formula za vsoto členov neskončne padajoče geometrijske progresije. Če je prvi člen napredovanja b in je imenovalec q tak, da je 0< q < 1 , то сумма равна b 1 - q .

Oglejmo si nekaj primerov z uporabo te formule.

Primer 12. Pretvarjanje periodičnega decimalnega ulomka v navadni ulomek

Naj imamo periodični ulomek 0, (8) in ga moramo pretvoriti v navadni ulomek.

0 , (8) = 0 , 8 + 0 , 08 + 0 , 008 + . .

Tukaj imamo neskončno padanje geometrijsko napredovanje s prvim členom 0, 8 in imenovalcem 0, 1.

Uporabimo formulo:

0 , (8) = 0 , 8 + 0 , 08 + 0 , 008 + . . = 0 , 8 1 - 0 , 1 = 0 , 8 0 , 9 = 8 9

To je zahtevani navadni ulomek.

Za utrjevanje gradiva si oglejmo še en primer.

Primer 13. Pretvarjanje periodičnega decimalnega ulomka v navadni ulomek

Obrnimo ulomek 0, 43 (18).

Najprej zapišemo ulomek kot neskončno vsoto:

0 , 43 (18) = 0 , 43 + (0 , 0018 + 0 , 000018 + 0 , 00000018 . .)

Poglejmo izraze v oklepajih. To geometrijsko progresijo lahko predstavimo na naslednji način:

0 , 0018 + 0 , 000018 + 0 , 00000018 . . = 0 , 0018 1 - 0 , 01 = 0 , 0018 0 , 99 = 18 9900 .

Rezultat prištejemo končnemu ulomku 0, 43 = 43 100 in dobimo rezultat:

0 , 43 (18) = 43 100 + 18 9900

Po seštevanju teh ulomkov in zmanjševanju dobimo končni odgovor:

0 , 43 (18) = 19 44

Za zaključek tega članka bomo rekli, da neperiodičnih neskončnih decimalnih ulomkov ni mogoče pretvoriti v navadne ulomke.

Če v besedilu opazite napako, jo označite in pritisnite Ctrl+Enter

V prejšnjem delu smo si ogledali ulomke z vsemi vrstami imenovalcev in jih poimenovali navadni ulomki. Zanimal nas je vsak ulomek, ki je nastal v procesu merjenja ali deljenja, ne glede na to, kateri imenovalec smo na koncu dobili.

Sedaj bomo iz celotne množice ulomkov izločili ulomke z imenovalci: 10, 100, 1000, 10.000 itd., torej takšne ulomke, katerih imenovalec so le števila, ki jih predstavlja ena (1), ki ji sledijo ničle (ena ali več ). Takšni ulomki se imenujejo decimalno.

Tukaj so primeri decimalnih ulomkov:

Z decimalnimi ulomki smo se že srečali, vendar nismo navedli nobenih posebnih lastnosti, ki so jim lastne. Zdaj bomo pokazali, da imajo nekaj izjemnih lastnosti, ki poenostavljajo vse izračune z ulomki.

§ 103. Podoba decimalnega ulomka brez imenovalca.

Decimalni ulomki se običajno ne pišejo na enak način kot navadni ulomki, ampak po pravilih, po katerih se zapisujejo cela števila.

Če želite razumeti, kako napisati decimalni ulomek brez imenovalca, se morate spomniti, kako pisati decimalni sistem poljubno celo število. Če na primer zapišemo trimestno število samo s številko 2, torej s številko 222, bo imela vsaka od teh dvojk poseben pomen odvisno od mesta, ki ga zaseda v številu. Prvi dve na desni strani pomenita enote, druga desetice in tretja stotine. Tako katera koli števka levo od katere koli druge števke označuje desetkrat večje enote od tistih, ki jih označuje prejšnja števka. Če katera številka manjka, se na njeno mesto vpiše ničla.

Torej so v celem številu enote na prvem mestu na desni, desetice na drugem itd.

Zdaj pa se vprašajmo, katero števko enot bomo dobili, če smo na primer v številu 222 s desno Dodajmo še eno številko ob strani. Za odgovor na to vprašanje morate upoštevati, da zadnja dva (prvi z desne) predstavljata enice.

Torej, če za dvema, ki označujeta enote, nekoliko stopimo nazaj, napišemo kakšno drugo številko, na primer 3, bo to pomenilo enote, desetkrat manjši od prejšnjih, z drugimi besedami, to bo pomenilo desetine enote; rezultat je število, ki vsebuje 222 celih enot in 3 desetinke enote.

Sprejeto med celoto in delni delštevilke postavite z vejico, tj. napišite takole:

Če temu številu za tremi dodamo še eno številko, na primer 4, bo to pomenilo 4 stotink deli enote; številka bo izgledala takole:

in se izgovarja: dvesto dvaindvajset pika štiriintrideset.

Nova figura, na primer 5, ki je dodeljen tej številki, nam daje tisočinke: 222.345 (dvesto dvaindvajset pika tristo petinštirideset tisočink).

Za večjo jasnost lahko razporeditev števila celih in delnih števk predstavimo v obliki tabele:

Tako smo razložili, kako se zapišejo decimalni ulomki brez imenovalca. Zapišimo nekaj teh ulomkov.

Če želite zapisati ulomek 5/10 brez imenovalca, morate upoštevati, da nima celih števil in mora biti zato mesto celih števil zasedeno z ničlo, to je 5/10 = 0,5.

Ulomek 2 9 / 100 brez imenovalca bo zapisan takole: 2,09, torej namesto desetin morate postaviti nič. Če bi to 0 izpustili, bi dobili povsem drugačen ulomek, in sicer 2,9, torej dve celi in devet desetin.

To pomeni, da morate pri pisanju decimalnih ulomkov označiti manjkajoča cela števila in ulomke:

0,325 - brez celih števil,
0,012 - brez celih števil in brez desetin,
1.208 - brez stotink,
0,20406 - brez celih števil, brez stotink in brez desettisočink.

Številke desno od decimalne vejice imenujemo decimalne številke.

Da bi se izognili napakam pri pisanju decimalnih ulomkov, si morate zapomniti, da mora biti za decimalno vejico na sliki decimalnega ulomka toliko števil, kolikor ničel bi bilo v imenovalcu, če bi ta ulomek zapisali z imenovalcem, tj.

0,1 = 1/10 (v imenovalcu je ena ničla, za decimalno vejico pa ena številka);

§ 104. Pripisovanje ničel decimalnim ulomkom.

V prejšnjem odstavku je bilo opisano, kako so predstavljeni decimalni ulomki brez imenovalcev. Velika vrednost ima pri pisanju decimalnih ulomkov ničlo. Vsak pravi decimalni ulomek ima namesto celih števil ničlo, kar pomeni, da ulomek nima celih števil. Sedaj bomo zapisali več različnih decimalnih ulomkov s števili: 0, 3 in 5.

0,35 - 0 celo, 35 stotink,
0,035 - 0 celo, 35 tisočink,
0,305 - 0 celo, 305 tisočink,
0,0035 - 0 celo, 35 desettisočink.

Ugotovimo zdaj, kakšen pomen imajo ničle na koncu decimalnega ulomka, torej na desni.

Če vzamemo celo število, na primer 5, za njim postavimo vejico in nato za vejico napišemo ničlo, bo ta ničla pomenila nič desetin. Posledično ta ničla, dodeljena desni, ne bo vplivala na vrednost števila, tj.

Sedaj vzemimo številko 6.1 in ji dodamo ničlo desno, dobimo 6.10, torej imeli smo 1/10 za decimalno vejico, vendar je postalo 10/100, vendar je 10/100 enako 1/10. To pomeni, da se velikost števila ni spremenila, od dodajanja ničle na desno pa sta se spremenila samo videz števila in izgovorjava (6.1 - šest pika ena desetina; 6.10 - šest pika ena deset stotink).

S podobnim razmišljanjem se lahko prepričamo, da dodajanje ničel desno od decimalnega ulomka ne spremeni njegove vrednosti. Zato lahko zapišemo naslednje enačbe:

1 = 1,0,
2,3 = 2,300,
6,7 = 6,70000 itd.

Če dodamo ničle levo od decimalnega ulomka, potem ne bodo imele nobenega pomena. Pravzaprav, če levo od številke 4,6 zapišemo nič, bo številka dobila obliko 04,6. Kje je ničla? Stoji na mestu desetic, torej kaže, da v tem številu ni desetic, vendar je to jasno tudi brez ničle.

Vendar je treba zapomniti, da se včasih na desno od decimalnih ulomkov dodajo ničle. Na primer, obstajajo štirje ulomki: 0,32; 2,5; 13.1023; 5,238. Tistim ulomkom, ki imajo za decimalno vejico manj decimalk, pripišemo ničle na desni strani: 0,3200; 2,5000; 13.1023; 5,2380.

Zakaj je to storjeno? Z dodajanjem ničel na desno smo za vsako številko dobili štiri števke za decimalno vejico, kar pomeni, da bo imel vsak ulomek imenovalec 10.000, pred dodajanjem ničl pa je bil imenovalec prvega ulomka 100, drugega 10, tretji je bil 10.000, četrti pa 1.000. Tako smo z dodajanjem ničel izenačili število decimalnih mest naših ulomkov, tj. skupni imenovalec. Zato se decimalni ulomki spravijo na skupni imenovalec tako, da se tem ulomkom dodajo ničle.

Po drugi strani pa, če ima kateri koli decimalni ulomek ničle na desni, jih lahko zavržemo, ne da bi spremenili njegovo vrednost, na primer: 2,60 = 2,6; 3,150 = 3,15; 4.200 = 4,2.

Kako naj razumemo to spuščanje ničel desno od decimalnega ulomka? Enakovredno je njegovemu zmanjševanju in to lahko vidimo, če te decimalne ulomke zapišemo z imenovalcem:

§ 105. Primerjava decimalnih ulomkov po velikosti.

Pri uporabi decimalnih ulomkov je zelo pomembno, da znamo ulomke med seboj primerjati in odgovoriti na vprašanje, kateri so enaki, kateri večji in kateri manjši. Primerjava decimalnih mest deluje drugače kot primerjava celih števil. Na primer cela dvomestno število je vedno večje od ene števke, ne glede na to, koliko enot vsebuje enomestno število; Trimestno število je večje od dvomestnega, še bolj pa od enomestnega. Toda pri primerjavi decimalnih mest bi bilo napačno šteti vse znake, v katerih so zapisani ulomki.

Vzemimo dva ulomka: 3,5 in 2,5 in ju primerjajmo po velikosti. Imata enaka decimalna mesta, vendar ima prvi ulomek 3 cela števila, drugi pa 2. Prvi ulomek je večji od drugega, tj.

Vzemimo še druge ulomke: 0,4 in 0,38. Za primerjavo teh ulomkov je koristno dodati ničlo na desno od prvega ulomka. Nato bomo primerjali ulomka 0,40 in 0,38. Vsak od njih ima dve števki za decimalno vejico: to pomeni, da imajo ti ulomki enak imenovalec 100.

Le primerjati moramo njihove števce, a števec 40 je večji od 38. To pomeni, da je prvi ulomek večji od drugega, tj.

Prvi ulomek ima več desetin kot drugi, čeprav ima drugi ulomek 8 stotink več, vendar so manjše od ene desetine, ker je 1/10 = 10/100.

Primerjajmo sedaj naslednja ulomka: 1,347 in 1,35. Desno drugemu ulomku dodajmo ničlo in primerjajmo decimalna ulomka: 1,347 in 1,350. Njihovi celi deli so enaki, kar pomeni, da je treba primerjati samo delne dele: 0,347 in 0,350. Ti ulomki imajo skupni imenovalec, vendar je števec drugega ulomka večji od števca prvega, kar pomeni, da je drugi ulomek večji od prvega, to je 1,35 > 1,347.

Za konec primerjajmo še dva ulomka: 0,625 in 0,62473. Prvemu ulomku prištejmo dve ničli, da izenačimo števke, in primerjajmo dobljena ulomka: 0,62500 in 0,62473. Njuna imenovalca sta enaka, vendar je števec prvega ulomka 62.500 večji od števca drugega ulomka 62.473, zato je prvi ulomek večji od drugega, to je 0,625 > 0,62473.

Na podlagi navedenega lahko potegnemo naslednji sklep: od dveh decimalnih ulomkov je večji tisti, ki ima večje število celih števil; kadar so cela števila enaka, je večji tisti ulomek, ki ima večje število desetin; kadar so cela števila in desetinke enake, je ulomek z večjim številom stotink večji itd.

§ 106. Povečanje in zmanjševanje decimalnega ulomka za 10, 100, 1000 itd.

Vemo že, da dodajanje ničel decimalki ne vpliva na njeno vrednost. Ko smo preučevali cela števila, smo videli, da vsaka ničla, dodana na desno, poveča število za 10-krat. Ni težko razumeti, zakaj se je to zgodilo. Če vzamemo celo število, na primer 25, in mu na desni dodamo ničlo, se bo število povečalo 10-krat, število 250 je 10-krat večje od 25. Ko se je na desni pojavila ničla, se je število 5, ki je prej označevali enote, zdaj začeli označevati desetice, številka 2, ki je prej označevala desetice, pa je postala stotica. To pomeni, da so zaradi pojava ničle prejšnje številke zamenjale nove, postale so večje, premaknile so se za eno mesto v levo. Ko moramo decimalni ulomek povečati na primer za 10-krat, moramo števke premakniti tudi za eno mesto v levo, vendar tega premika ni mogoče doseči z ničlo. Decimalni ulomek je sestavljen iz celega in ulomka, meja med njima pa je vejica. Levo od decimalne vejice je najnižja cela številka, desno pa najvišja delna številka. Razmislite o ulomku:

Kako lahko številke v njem premaknemo vsaj za eno mesto, z drugimi besedami, kako ga povečamo za 10-krat? Če premaknemo vejico za eno mesto v desno, bo to najprej vplivalo na usodo petice: premakne se iz območja delnih števil v območje celih števil. Številka bo potem videti takole: 12345.678. Sprememba se je zgodila pri vseh drugih številkah, ne le pri petici. Začele so se predvajati vse številke, vključene v številko novo vlogo, se je zgodilo naslednje (glej tabelo):

Vsi čini so se preimenovali, vse enote činov pa so tako rekoč napredovale eno mesto višje. Od tega se je celotno število povečalo za 10-krat. Če premaknete decimalno mesto za eno mesto v desno, se število poveča za 10-krat.

Oglejmo si še nekaj primerov:

1) Vzemite ulomek 0,5 in premaknite decimalno vejico eno mesto v desno; dobimo število 5, ki je 10-krat večje od 0,5, ker je prej pet označevalo desetinke enote, zdaj pa cele enote.

2) Premaknite decimalno vejico v številu 1,234 za dve mesti v desno; številka bo postala 123,4. To število je 100-krat večje od prejšnjega, ker je v njem številka 3 začela označevati enote, številka 2 - desetice in številka 1 - stotine.

Torej, če želite decimalni ulomek povečati za 10-krat, morate premakniti decimalno mesto eno mesto v desno; če ga želite povečati 100-krat, morate premakniti decimalno vejico za dve mesti v desno; povečati za 1000-krat - tri števke na desno itd.

Če številka nima dovolj znakov, se ji na desni dodajo ničle. Na primer, povečajmo ulomek 1,5 za 100-krat tako, da premaknemo decimalno vejico na dve mesti; dobimo 150. Povečajmo ulomek 0,6 za 1000-krat; dobimo 600.

Po potrebi nazaj zmanjšanje decimalni ulomek za 10, 100, 1000 itd. krat, potem morate premakniti decimalno vejico v levo za eno, dve, tri itd. Naj bo podan ulomek 20,5; Zmanjšajmo ga za 10-krat; Če želite to narediti, premaknite decimalno vejico eno mesto v levo, ulomek bo imel obliko 2,05. Zmanjšajmo ulomek 0,015 za 100-krat; dobimo 0,00015. Zmanjšajmo število 334 za 10-krat; dobimo 33,4.

V obliki:

± d m … d 1 d 0 , d -1 d -2 …

kjer je ± znak za ulomek: bodisi + ali -,

, je decimalna vejica, ki služi kot ločilo med celim in ulomkom števila,

dk- decimalna števila.

Hkrati ima vrstni red števil pred decimalno vejico (levo od nje) konec (kot min 1 na števko), za decimalno vejico (desno) pa je lahko oboje končno (alternativno tam ne sme vsebovati števk za decimalno vejico) in neskončno.

Decimalna vrednost ± d m … d 1 d 0 , d -1 d -2 … je realno število:

ki je enak vsoti končnega ali neskončnega števila členov.

Učinkovitost realna števila uporaba decimalnih ulomkov je posplošitev zapisovanja celih števil v decimalnem številskem sistemu. Decimalna predstavitev celega števila nima števk za decimalno vejico, zato je predstavitev videti takole:

± d m … d 1 d 0 ,

In to sovpada z zapisom našega števila v decimalnem številskem sistemu.

decimalno- to je rezultat deljenja 1 na 10, 100, 1000 in tako naprej. Ti ulomki so zelo priročni za izračune, ker temeljijo na istem položajnem sistemu, na katerem temeljita štetje in zapisovanje celih števil. Zahvaljujoč temu so zapis in pravila za delo z decimalnimi ulomki skoraj enaki kot pri celih številih.

Pri pisanju decimalnih ulomkov ni treba označevati imenovalca, določa ga mesto, ki ga zaseda ustrezna cifra. Najprej zapišemo cel del števila, nato pa na desno postavimo decimalno vejico. Prva številka za decimalno vejico označuje število desetin, druga - število stotink, tretja - število tisočin in tako naprej. Številke, ki se nahajajo za decimalno vejico, so decimalke.

Na primer:

Ena od prednosti decimalnih ulomkov je, da jih je mogoče zelo enostavno skrčiti na navadne ulomke: število za decimalno vejico (pri nas je to 5047) je števnik; imenovalec enako n-ta potenca števila 10, kjer n- število decimalnih mest (za nas je to n=4):

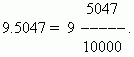
Kadar v decimalnem ulomku ni celega dela, pred decimalno vejico postavimo ničlo:

Lastnosti decimalnih ulomkov.

1. Decimalka se ne spremeni, ko se na desno dodajo ničle:

13.6 =13.6000.

2. Decimalka se ne spremeni, ko se odstranijo ničle na koncu decimalke:

0.00123000 = 0.00123.

Pozor! Ne morete odstraniti ničel, ki NISO na koncu decimalnega ulomka!

3. Decimalni ulomek se poveča za 10, 100, 1000 in tako naprej, ko decimalno vejico premaknemo na 1, 2, 2 in tako naprej v desno:

3,675 → 367,5 (ulomek povečan za stokrat).

4. Decimalni ulomek se zmanjša za deset, sto, tisoč in tako naprej, ko decimalno vejico premaknemo na 1, 2, 3 in tako naprej v levo:

1536,78 → 1,53678 (ulomek je postal tisočkrat manjši).

Vrste decimalnih ulomkov.

Decimalni ulomki so razdeljeni na dokončno, neskončno in periodične decimalke.

Zadnji decimalni ulomek je to je ulomek, ki vsebuje končno število števk za decimalno vejico (ali pa jih sploh ni), tj. izgleda takole:

Realno število je mogoče predstaviti kot končni decimalni ulomek le, če je to število racionalno in če je zapisano kot nezmanjšani ulomek p/q imenovalec q nima prafaktorjev razen 2 in 5.

Neskončna decimalka.

Vsebuje neskončno ponavljajočo se skupino klicanih številk obdobje. Pika je zapisana v oklepaju. Na primer, 0,12345123451234512345… = 0.(12345).

Periodični decimalni ulomek- to je neskončni decimalni ulomek, v katerem je zaporedje števk za decimalno vejico, začenši z določenega mesta, periodično ponavljajoča se skupina števk. Z drugimi besedami, periodični ulomek- decimalni ulomek, ki izgleda takole:

Takšen ulomek običajno na kratko zapišemo takole:

Skupina števil b 1 … b l, ki ponavlja, je obdobje ulomka, število števk v tej skupini je dolžina obdobja.

Če je v periodičnem ulomku pika takoj za decimalno vejico, to pomeni, da je ulomek čista periodika. Če so med decimalno vejico in 1. piko števila, potem je ulomek mešana periodika, skupina števk za decimalno vejico do 1. števke pike pa je ulomek predobdobje.

Na primer, je ulomek 1,(23) = 1,2323... čisto periodičen, ulomek 0,1(23) = 0,12323... pa je mešano periodičen.

Glavna lastnost periodičnih ulomkov, po čemer se ločijo od celotne množice decimalnih ulomkov, je v tem, da periodični ulomki in le ti predstavljajo racionalna števila. Natančneje se zgodi naslednje:

Vsak neskončno periodični decimalni ulomek predstavlja racionalno število. Nasprotno, ko racionalno število razširimo v neskončni decimalni ulomek, to pomeni, da bo ta ulomek periodičen.

To gradivo bomo posvetili takim pomembna tema, kot decimalke. Najprej opredelimo osnovne definicije, navedemo primere in se poglobimo v pravila decimalne notacije, pa tudi, kaj so števke decimalnih ulomkov. Nato izpostavimo glavne vrste: končni in neskončni, periodični in neperiodični ulomki. V zadnjem delu bomo pokazali, kako se točke, ki ustrezajo ulomkom, nahajajo na koordinatni osi.

Yandex.RTB R-A-339285-1

Kaj je decimalni zapis ulomkov

Tako imenovani decimalni zapis ulomkov lahko uporabljamo tako za naravna kot za ulomka. Videti je kot niz dveh ali več števil z vejico med njimi.

Decimalna vejica je potrebna za ločevanje celotnega dela od ulomka. Zadnja številka decimalnega ulomka praviloma ni ničla, razen če se decimalna vejica pojavi takoj za prvo ničlo.

Kateri so primeri ulomkov v decimalnem zapisu? To je lahko 34, 21, 0, 35035044, 0, 0001, 11.231.552, 9 itd.

V nekaterih učbenikih lahko najdete uporabo pike namesto vejice (5. 67, 6789. 1011 itd.). Ta možnost velja za enakovredno, vendar je bolj značilna za vire v angleškem jeziku.

Definicija decimalk

Na podlagi zgornjega koncepta decimalnega zapisa lahko formuliramo naslednja definicija decimalni ulomki:

Definicija 1

Decimalke predstavljajo ulomke v decimalnem zapisu.

Zakaj moramo ulomke pisati v tej obliki? Daje nam nekaj prednosti pred običajnimi, na primer bolj strnjen zapis, predvsem v primerih, ko je v imenovalcu 1000, 100, 10 itd., ali mešano število. Na primer, namesto 6 10 lahko določimo 0,6, namesto 25 10000 - 0,0023, namesto 512 3 100 - 512,03.

O tem, kako pravilno predstaviti navadne ulomke z desetinami, stotinami in tisoči v imenovalcu v decimalni obliki, bomo razpravljali v ločenem gradivu.

Kako pravilno brati decimalke

Obstaja nekaj pravil za branje decimalnih zapisov. Tako se tisti decimalni ulomki, ki jim ustrezajo običajni navadni ekvivalenti, berejo skoraj enako, vendar z dodatkom besed "nič desetin" na začetku. Tako se vnos 0, 14, ki ustreza 14.100, bere kot "nič pika štirinajst stotink."

Če lahko decimalni ulomek povežemo z mešanim številom, potem ga beremo na enak način kot to število. Torej, če imamo ulomek 56, 002, ki ustreza 56 2 1000, beremo ta vnos kot "šestinpetdeset in dve tisočinki."

Pomen števke v decimalnem ulomku je odvisen od tega, kje se nahaja (enako kot pri naravnih številih). Torej, v decimalnem ulomku 0,7 je sedem desetin, v 0,0007 desettisočink, v ulomku 70.000,345 pa pomeni sedem desettisočev celih enot. Tako v decimalnih ulomkih obstaja tudi koncept mestne vrednosti.

Imena števk pred decimalno vejico so podobna tistim, ki obstajajo v naravnih številih. Imena tistih, ki se nahajajo za tem, so jasno predstavljena v tabeli:

Poglejmo si primer.

Primer 1

Imamo decimalni ulomek 43.098. Ima štirico na mestu desetic, trojko na mestu enic, ničlo na mestu desetin, 9 na mestu stotink in 8 na mestu tisočink.

Običajno je, da se stopnje decimalnih ulomkov razlikujejo po prednosti. Če se premikamo po številkah od leve proti desni, bomo šli od najpomembnejših do najmanj pomembnih. Izkazalo se je, da so stotice starejše od desetin, deli na milijon pa so mlajši od stotink. Če vzamemo zadnji decimalni ulomek, ki smo ga navedli kot zgornji primer, bo najvišje ali najvišje mesto v njem stotinica, najnižje ali najnižje mesto pa 10-tisočinka.

Vsak decimalni ulomek je mogoče razširiti na posamezne števke, to je predstaviti kot vsoto. To dejanje se izvede na enak način kot za naravna števila.

Primer 2

Poskusimo ulomek 56, 0455 razširiti na števke.

Dobili bomo:

56 , 0455 = 50 + 6 + 0 , 4 + 0 , 005 + 0 , 0005

Če se spomnimo lastnosti seštevanja, lahko ta ulomek predstavimo v drugih oblikah, na primer kot vsoto 56 + 0, 0455 ali 56, 0055 + 0, 4 itd.

Kaj so končne decimalke?

Vsi ulomki, o katerih smo govorili zgoraj, so končne decimalke. To pomeni, da je število števk za decimalno vejico končno. Izpeljimo definicijo:

Definicija 1

Končne decimalne številke so vrsta decimalnih ulomkov, ki imajo za decimalnim znakom končno število decimalnih mest.

Primeri takšnih ulomkov so lahko 0, 367, 3, 7, 55, 102567958, 231 032, 49 itd.

Vsak od teh ulomkov je mogoče pretvoriti v mešano število (če je vrednost njihovega ulomka različna od nič) ali v navaden ulomek (če je celo število nič). O tem, kako se to naredi, smo posvetili poseben članek. Tukaj bomo izpostavili le nekaj primerov: na primer, končni decimalni ulomek 5, 63 lahko zmanjšamo na obliko 5 63 100, 0, 2 pa ustreza 2 10 (ali kateremu koli drugemu ulomku, ki mu je enak, za na primer 4 20 ali 1 5.)

Toda obraten proces, tj. pisanje navadnega ulomka v decimalni obliki morda ni vedno mogoče. Torej 5 13 ni mogoče nadomestiti z enakim ulomkom z imenovalcem 100, 10 itd., kar pomeni, da iz njega ni mogoče dobiti končnega decimalnega ulomka.

Glavne vrste neskončnih decimalnih ulomkov: periodični in neperiodični ulomki

Zgoraj smo navedli, da se končni ulomki tako imenujejo, ker imajo končno število števk za decimalno vejico. Vendar pa je lahko neskončno, v tem primeru se bodo tudi sami ulomki imenovali neskončni.

Definicija 2

Neskončni decimalni ulomki so tisti, ki imajo za decimalno vejico neskončno število števk.

Očitno takšnih številk preprosto ni mogoče zapisati v celoti, zato navedemo le del njih in nato dodamo elipso. Ta znak označuje neskončno nadaljevanje zaporedja decimalnih mest. Primeri neskončnih decimalnih ulomkov vključujejo 0, 143346732…, ​​​​3, 1415989032…, 153, 0245005…, 2, 66666666666…, 69, 748768152…. itd.

"Rep" takega ulomka lahko vsebuje ne le navidezno naključna zaporedja števil, ampak tudi stalno ponavljanje istega znaka ali skupine znakov. Ulomki z izmeničnimi številkami za decimalno vejico se imenujejo periodični.

Definicija 3

Periodični decimalni ulomki so tisti neskončni decimalni ulomki, v katerih se za decimalno vejico ponavlja ena števka ali skupina več števk. Ponavljajoči se del imenujemo obdobje ulomka.

Na primer, za ulomek 3, 444444.... obdobje bo številka 4, za 76 pa 134134134134... - skupina 134.

Kakšno je najmanjše število znakov, ki jih lahko pustimo v zapisu periodičnega ulomka? Za periodične ulomke bo dovolj, če celotno periodo enkrat zapišemo v oklepaj. Torej, ulomek 3, 444444…. Pravilno bi bilo zapisati kot 3, (4), in 76, 134134134134 ... - kot 76, (134).

Na splošno imajo vnosi z več točkami v oklepajih popolnoma enak pomen: na primer, periodični ulomek 0,677777 je enak 0,6 (7) in 0,6 (77) itd. Sprejemljivi so tudi zapisi v obliki 0, 67777 (7), 0, 67 (7777) itd.

Da bi se izognili napakam, uvajamo enotnost zapisa. Dogovorimo se, da zapišemo samo eno piko (najkrajše možno zaporedje številk), ki je najbližje decimalni vejici, in jo zapičimo v oklepaj.

To pomeni, da bomo za zgornji ulomek menili, da je glavni vnos 0, 6 (7), in na primer v primeru ulomka 8, 9134343434, bomo zapisali 8, 91 (34).

Če imenovalec navadnega ulomka vsebuje prafaktorje, ki niso enaki 5 in 2, potem pri pretvorbi v decimalni zapis spremenili se bodo v neskončne frakcije.

Načeloma lahko vsak končni ulomek zapišemo kot periodičnega. Da bi to naredili, moramo samo dodati neskončno število ničel na desno. Kako izgleda na posnetku? Recimo, da imamo zadnji ulomek 45, 32. V periodični obliki bo videti kot 45, 32 (0). To dejanje je možno, ker dodajanje ničel na desno od katerega koli decimalnega ulomka daje rezultat, ki mu je enak.

Posebno pozornost je treba nameniti periodičnim ulomkom z obdobjem 9, na primer 4, 89 (9), 31, 6 (9). So alternativni zapis za podobne ulomke s periodo 0, zato jih pogosto zamenjamo pri pisanju z ulomki s periodo nič. V tem primeru se vrednosti naslednje številke prišteje ena, v oklepaju pa je navedena (0). Enakost dobljenih števil lahko enostavno preverimo tako, da jih predstavimo kot navadne ulomke.

Na primer, ulomek 8, 31 (9) lahko nadomestite z ustreznim ulomkom 8, 32 (0). Ali 4, (9) = 5, (0) = 5.

Neskončni decimalni periodični ulomki se nanašajo na racionalna števila. Z drugimi besedami, vsak periodični ulomek je mogoče predstaviti kot navaden ulomek in obratno.

Obstajajo tudi ulomki, ki nimajo neskončno ponavljajočega se zaporedja za decimalno vejico. V tem primeru se imenujejo neperiodični ulomki.

Definicija 4

Med neperiodične decimalne ulomke uvrščamo tiste neskončne decimalne ulomke, ki ne vsebujejo pike za decimalno vejico, tj. ponavljajoča se skupina številk.

Včasih so neperiodični ulomki zelo podobni periodičnim. Na primer 9, 03003000300003 ... na prvi pogled se zdi, da ima piko, vendar podrobna analiza decimalnih mest potrjuje, da je to še vedno neperiodični ulomek. S takimi številkami morate biti zelo previdni.

Neperiodični ulomki se nanašajo na iracionalna števila. Niso pretvorjeni v navadne ulomke.

Osnovne operacije z decimalkami

Z decimalnimi ulomki lahko izvajamo naslednje operacije: primerjanje, odštevanje, seštevanje, deljenje in množenje. Oglejmo si vsakega od njih posebej.

Primerjavo decimalk lahko zmanjšamo na primerjavo ulomkov, ki ustrezajo prvotnim decimalkam. Toda neskončnih neperiodičnih ulomkov ni mogoče reducirati na to obliko in pretvorba decimalnih ulomkov v navadne ulomke je pogosto delovno intenzivna naloga. Kako lahko hitro izvedemo primerjalno dejanje, če moramo to narediti med reševanjem problema? Primerjamo decimalne ulomke s števko na enak način, kot primerjamo naravna števila. Tej metodi bomo posvetili poseben članek.

Če želite nekatere decimalne ulomke sešteti z drugimi, je priročno uporabiti metodo seštevanja stolpcev, kot za naravna števila. Če želite dodati periodične decimalne ulomke, jih morate najprej zamenjati z navadnimi in šteti po standardni shemi. Če moramo glede na pogoje problema sešteti neskončno število neperiodičnih ulomkov, jih moramo najprej zaokrožiti na določeno števko in nato sešteti. Čim manjša je številka, na katero zaokrožimo, tem večja bo točnost izračuna. Za odštevanje, množenje in deljenje neskončnih ulomkov je potrebno tudi predhodno zaokroževanje.

Iskanje razlike med decimalnimi ulomki je inverzna seštevanju. V bistvu lahko z odštevanjem najdemo število, katerega vsota z ulomkom, ki ga odštevamo, nam bo dala ulomek, ki ga minimiziramo. O tem bomo podrobneje govorili v ločenem članku.

Množenje decimalnih ulomkov poteka na enak način kot pri naravnih številih. Za to je primerna tudi metoda izračuna stolpcev. To dejanje s periodičnimi ulomki spet zmanjšamo na množenje navadnih ulomkov po že preučenih pravilih. Neskončne ulomke, kot se spomnimo, je treba pred izračuni zaokrožiti.

Postopek deljenja decimalnih ulomkov je obraten proces množenje. Pri reševanju nalog uporabljamo tudi stolpčno računanje.

Lahko vzpostavite natančno ujemanje med končnim decimalnim ulomkom in točko na koordinatni osi. Ugotovimo, kako označiti točko na osi, ki bo natančno ustrezala zahtevanemu decimalnemu ulomku.

Preučili smo že, kako konstruirati točke, ki ustrezajo navadnim ulomkom, vendar je mogoče decimalne ulomke reducirati na to obliko. Na primer, navadni ulomek 14 10 je enak 1, 4, zato bo ustrezna točka odmaknjena od izhodišča v pozitivni smeri za popolnoma enako razdaljo:

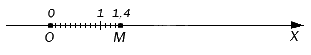
Lahko storite, ne da bi zamenjali decimalni ulomek z navadnim, ampak kot osnovo uporabite metodo razširitve s števkami. Torej, če moramo označiti točko, katere koordinata bo enaka 15, 4008, potem bomo to številko najprej predstavili kot vsoto 15 + 0, 4 +, 0008. Za začetek odložimo 15 celih segmentov enote v pozitivni smeri od začetka odštevanja, nato 4 desetinke enega segmenta in nato 8 desettisočink enega segmenta. Kot rezultat dobimo koordinatno točko, ki ustreza ulomku 15, 4008.

Za neskončni decimalni ulomek je bolje uporabiti to metodo, saj vam omogoča, da se čim bolj približate želeni točki. V nekaterih primerih je mogoče zgraditi natančno ujemanje z neskončnim ulomkom na koordinatni osi: na primer 2 = 1, 41421. . . , in ta ulomek lahko povežemo s točko na koordinatnem žarku, ki je od 0 oddaljena za dolžino diagonale kvadrata, katere stranica bo enaka enemu segmentu enote.

Če na osi ne najdemo točke, temveč decimalni ulomek, ki ji ustreza, se to dejanje imenuje decimalna meritev segmenta. Poglejmo, kako to storiti pravilno.

Recimo, da moramo priti od nič do dane točke na koordinatni osi (ali priti čim bližje v primeru neskončni ulomek). Da bi to naredili, postopoma odlagamo segmente enote od izhodišča, dokler ne pridemo do želene točke. Po celih segmentih po potrebi odmerimo desetinke, stotinke in manjše delčke, da je ujemanje čim bolj natančno. Kot rezultat smo prejeli decimalni ulomek, ki ustreza dano točko na koordinatni osi.

Zgoraj smo prikazali risbo s točko M. Poglejte še enkrat: da pridete do te točke, morate izmeriti en segment enote in štiri desetinke od nič, saj ta točka ustreza decimalnemu ulomku 1, 4.

Če v procesu decimalne meritve ne moremo priti do točke, potem to pomeni, da ustreza neskončnemu decimalnemu ulomku.

Če v besedilu opazite napako, jo označite in pritisnite Ctrl+Enter