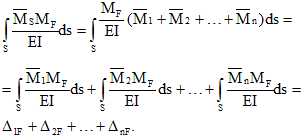Aprēķiniet plakanu statiski nenoteiktu stieņu sistēmu. Statiski nenoteiktu sistēmu aprēķins ar spēka metodi

Statiski nenoteiktas sistēmas sauc par stieņu sistēmām, lai noteiktu balstu reakcijas, kurās nepietiek tikai ar līdzsvara vienādojumiem. No kinemātiskā viedokļa tās ir tādas stieņu sistēmas, kuru brīvības pakāpju skaits ir mazāks par saišu skaitu. Lai atklātu šādu sistēmu statisko nenoteiktību, nepieciešams sastādīt papildu deformācijas saderības vienādojumus. Šādu vienādojumu skaitu nosaka stieņu sistēmas statiskās nenoteiktības skaits. 8.14. attēlā parādīti statiski nenoteiktu siju un rāmju piemēri.

8.14b attēlā redzamais stars tiek saukts nepārtraukts staru kūlis. Šis nosaukums cēlies no tā, ka starpbalsts atbalsta tikai siju. Atbalsta punktā siju negriež eņģe, eņģe nav iegriezta sijas korpusā. Tāpēc spriegumu un deformāciju ietekme, ko sija piedzīvo kreisajā laidumā, ietekmē arī labo laidumu. Ja starpbalsta vietā sijas korpusā iegriež viru, tad rezultātā sistēma kļūs statiski determinēta - no viena sijas iegūsim divas viena no otras neatkarīgas sijas, no kurām katra būs statiski noteikta. . Jāņem vērā, ka vienlaidus sijas ir mazāk materiālu ietilpīgas salīdzinājumā ar sadalītajām sijām, jo ​​tās racionālāk sadala lieces momentus visā garumā. Šajā sakarā nepārtrauktās sijas tiek plaši izmantotas būvniecībā un inženierzinātnēs. Taču vienlaidu sijām, kas ir statiski nenoteiktas, ir nepieciešama īpaša aprēķina tehnika, kas ietver sistēmas deformāciju izmantošanu.

Pirms ķerties pie statiski nenoteiktu sistēmu aprēķina, ir jāiemācās noteikt to statiskās nenoteiktības pakāpi. Viens no vienkāršākajiem statiskās nenoteiktības pakāpes noteikšanas noteikumiem ir šāds:

, (8.3)

Kur  struktūrai uzlikto obligāciju skaits;  iespējamo neatkarīgo līdzsvara vienādojumu skaits, ko var sastādīt aplūkojamai sistēmai.

Mēs izmantojam vienādojumu (8.3), lai noteiktu 8.14. attēlā parādīto sistēmu statiskās nenoteiktības pakāpi.

8.14.a attēlā redzamais stars kādreiz ir bijis statiski nenoteikts, jo tam ir trīs saites uz kreisās kājas un viena saite labajā kājā. Šādam staram ir tikai trīs neatkarīgi līdzsvara vienādojumi. Tādējādi stara statiskās nenoteiktības pakāpe
. 8.14.b attēlā redzamais nepārtrauktais stars arī reiz ir statiski nenoteikts, jo tam ir divi savienojumi uz kreisā balsta un pa vienam savienojumam uz starpbalsta un uz labā balsta - kopā četri savienojumi. Tādējādi tās statiskās nenoteiktības pakāpe
.

Attēlā redzamais rāmis. 8.14c, ir trīs reizes statiski nenoteikts, jo tā balstos ir sešas saites. Šim kadram ir tikai trīs neatkarīgi līdzsvara vienādojumi. Tādējādi statiskās nenoteiktības pakāpe šim kadram no vienādojuma (8.3) ir:
. 8.18. attēlā redzamā rāmja statiskās nenoteiktības pakāpe d ir vienāda ar četriem, jo ​​rāmim ir septiņi savienojumi uz balstiem. Tāpēc tā statiskās nenoteiktības pakāpe ir vienāda ar
.

Noteikums (8.3.) statiskās nenoteiktības pakāpes noteikšanai tiek izmantots tikai vienkāršām sistēmām. Sarežģītākos gadījumos šis noteikums nedarbojas. 8.15. attēlā parādīts kadrs, kura statiskās nenoteiktības pakāpi nevar noteikt, izmantojot vienādojumu (8.3).

Ārēji 8.15. attēlā redzamā sistēma ir piecas reizes statiski nenoteikta. To ir viegli noteikt, izmantojot vienādojumu (8.3): no sešām ārējām saitēm (trīs A sadaļā, trīs B sadaļā un divas C sadaļā) tiek atņemti trīs iespējamie līdzsvara vienādojumi. Tomēr šai sistēmai ir arī iekšēja statiskā nenoteiktība. Iekšējo statisko nenoteiktību nav iespējams ņemt vērā, izmantojot vienādojumu (8.3). Pirms pāriet uz 8.15. attēlā redzamā rāmja statiskās nenoteiktības pakāpes noteikšanu, mēs ieviešam vairākas definīcijas. Pirmā no šīm definīcijām ietver vienkāršu viru jēdzienu.

Vienkārši sauc par viru, kas savieno divus stieņus (8.16. att.).

8.16.att. vienkārša eņģe

Tiek saukta vira, kas savieno vairākus stieņus grūti(8.17. att.).

8.17.att. sarežģīta eņģe

Vienkāršo eņģu skaitu, kas var aizstāt vienu sarežģītu viru, nosaka pēc formulas:

, (8.4)

Kur
- mezglā iekļauto stieņu skaits.

8.17. attēlā redzamo komplekso viru pārrēķinām uz vienkāršu eņģu skaitu, izmantojot formulu (8.4):
. Tādējādi 8.17. attēlā redzamo sarežģīto viru var aizstāt ar četrām vienkāršām eņģēm.

Ieviesīsim vēl vienu jēdzienu - slēgta cilpa.

Pierādīsim teorēmu: jebkura slēgta cilpa ir trīs reizes statiski nenoteikta.

Lai pierādītu teorēmu, apsveriet slēgtu ķēdi, kas noslogota ar ārējiem spēkiem (8.18. att.).

Izgriezīsim slēgtu kontūru ar vertikālu griezumu un parādīsim iekšējo spēka faktorus, kas rodas griezuma vietā. Katrā no sekcijām rodas trīs iekšējie faktori: bīdes spēks , lieces moments
un gareniskais spēks
. Kopumā katru no kontūras nogrieztajām daļām papildus ārējiem spēkiem ietekmē seši iekšējie faktori (8.18. att., b, c). Ņemot vērā vienas no nogrieztās daļas līdzsvaru, piemēram, kreiso (8.18. att., b), atklājam, ka uzdevums ir trīs reizes statiski nenoteikts, jo griezumam var sastādīt tikai trīs neatkarīgus līdzsvara vienādojumus. -nogriezto daļu, un uz nogriezto daļu iedarbojas seši nezināmi spēki. Tādējādi slēgtas cilpas statiskās nenoteiktības pakāpe ir vienāda ar
. Teorēma ir pierādīta.

Tagad, izmantojot vienkāršas eņģes un slēgtas cilpas jēdzienu, mēs varam formulēt vēl vienu noteikumu statiskās nenoteiktības pakāpes noteikšanai:

, (8.5)

Kur
 slēgto cilpu skaits;
 eņģu skaits vienkāršo (8.4).

Izmantojot vienādojumu (8.5), nosakām 8.15. attēlā redzamā rāmja statiskās nenoteiktības pakāpi. Rāmim ir piecas kontūras
, ieskaitot kontūru, ko veido atbalsta stieņi. Eņģes mezglā D ir vienkārša, jo tā savieno divus stieņus. Eņģes sadaļā K ir sarežģītas, jo tās savieno četrus stieņus. Vienkāršo eņģu skaits, kas varētu aizstāt eņģes sadaļā K, ir saskaņā ar formulu (8.4):
. Eņģe C ir arī sarežģīta, jo tā savieno trīs stieņus. Šai virai
. Turklāt sistēmai ir vēl divas vienkāršas eņģes, ar kurām tā tiek piestiprināta pie pamatnes. Tādējādi vienkāršo eņģu skaits sistēmā ir
. Slēgto cilpu skaita aizstāšana
un vienkāršu eņģu skaits
formulā (8.5) nosakām kadra statiskās nenoteiktības pakāpi:
. Tādējādi, kas parādīts attēlā. 8.15 kadrs, septiņas reizes statiski nenoteikts. Un tas nozīmē, ka, lai aprēķinātu šādu sistēmu, papildus trim līdzsvara vienādojumiem ir jāsastāda septiņi deformāciju saderības vienādojumi. Atrisinot šādi iegūto 10 vienādojumu sistēmu attiecībā pret šajos vienādojumos ietvertajiem nezināmajiem, iespējams noteikt gan ārējo saišu reakciju lielumu, gan rāmī radušos iekšējos spēkus. Šīs problēmas risināšanas procedūru var nedaudz vienkāršot, izslēdzot līdzsvara vienādojumus no vienādojumu sistēmas. Tomēr šī pieeja prasa izmantot īpašas risināšanas metodes, no kurām viena ir spēka metode.

Par statiski nenoteiktām sauc sistēmas, kurās iekšējos spēkus nevar noteikt tikai no līdzsvara vienādojumiem (statiskajiem vienādojumiem).

Statiski nenoteiktām konstrukcijām ir t.s lieki savienojumiem. Tie var rasties balstos, stieņos un citos elementos. Šādus savienojumus sauc par “liekiem”, jo tie nav nepieciešami konstrukcijas līdzsvara nodrošināšanai, bet tos nosaka tās stiprības un stingrības prasības. Tādus papildu savienojumus sauc ārējā. Turklāt paša dizaina iezīmju dēļ var rasties nevajadzīgi savienojumi. Piemēram, slēgta rāmja kontūra (46. att., G) katrā sekcijā ir trīs nezināmi iekšējie spēki, t.i. tikai seši, un trīs no tiem ir "papildus". Šo papildu piepūli sauc iekšējais. Atbilstoši ārējo vai iekšējo "papildu" savienojumu skaitam tie tiek izveidoti sistēmas statiskās nenoteiktības pakāpe. Tas ir vienāds ar starpību starp nosakāmo nezināmo skaitu un statisko vienādojumu skaitu. Ar vienu "papildu" nezināmo sistēmu vienreiz sauc par statiski nenoteiktu, ar diviem - divreiz par statiski nenoteiktu utt.

Attēlā parādītais dizains. 46, A, reiz ir statiski nenoteikts, un konstrukcijas, kas parādītas zīm. 46, b Un V, - divreiz statiski nenoteikts, attēlā. 46, d - trīs reizes ar statiski nenoteiktu konstrukciju.

Risinot statiski nenoteiktus uzdevumus, papildus statiskajiem vienādojumiem tiek izmantoti vienādojumi, kas ņem vērā konstrukcijas elementu deformācijas.

Statiski nenoteiktu problēmu risināšanai ir vairākas metodes: pārvietojumu salīdzināšanas metode, spēka metode, pārvietojuma metode.

spēka metode

Aprēķinot statiski nenoteiktas sistēmas, spēkus uzskata par nezināmiem.

Aprēķins pēc spēka metode veic šādā secībā:

• 1. Iestatiet statiskās nenoteiktības pakāpi.
• 2. Noņemot "papildus" savienojumus, sākotnējā sistēma tiek aizstāta ar statiski noteiktu, t.s. galvenā sistēma. Var izveidot vairākas šādas sistēmas, vienlaikus ievērojot to ģeogrāfisko stāvokli

metriskā nemainīgums.

• 3. Galvenā sistēma ir noslogota ar noteiktiem ārējiem spēkiem un "papildu" nezināmiem spēkiem, kas aizstāj attālo savienojumu darbību, kā rezultātā līdzvērtīga sistēma.
• 4. Lai nodrošinātu sākotnējās un galvenās sistēmas līdzvērtību, nezināmie spēki ir jāizvēlas tā, lai galvenās sistēmas deformācijas neatšķirtos no sākotnējās statiski nenoteiktās sistēmas deformācijām. Šim nolūkam "lieko" nezināmo pielietojuma punktu nobīde to darbības virzienā tiek pielīdzināta nullei. No šādā veidā iegūtajiem papildu vienādojumiem tiek noteiktas "papildu" nezināmo spēku vērtības. Atbilstošo punktu pārvietojumu noteikšanu var veikt jebkurā veidā, taču labāk ir izmantot vispārīgāko Mohr metodi.
• 5. Pēc "papildu" nezināmo spēku vērtību noteikšanas tiek noteiktas reakcijas un uzzīmētas iekšējo spēku diagrammas, atlasīti posmi un pārbaudīta stiprība parastajā veidā.

Spēka metodes kanoniskie vienādojumi

Papildu pārvietojumu vienādojumus, kas izsaka nobīdes vienādību ar nulli "papildu" nezināmo virzienos, var ērti sastādīt t.s. kanoniskā forma tie. pēc noteikta parauga. Parādīsim to ar vienkāršākās statiski nenoteiktās sistēmas risināšanas piemēru (47. att., A).

Mēs izvēlamies konsoli kā galveno sistēmu, atmetot šarnīrveida atbalstu. Līdzvērtīga sistēma tiks iegūta pēc tās ārējā spēka T 7 un "papildu" nezināmā pielikšanas X(47. attēls, b).

Kanoniskais vienādojums, kas izsaka punkta nulles nobīdi IN no spēkiem F un X, gribu

No vienādojuma, kas mums ir

Sistēmai, kurai ir divi "papildu" savienojumi, kanonisko vienādojumu sistēmai ir šāda forma:

• 8 11 X 1 + b 12 ^2 + ^1
• 621-^1 + 622^2 "I" ^20-

Kustības A[p Un b [y, kas iekļauti kanoniskajos vienādojumos, nosaka ar Mora metodi.

Sistēmām, kas sastāv no taisnvirziena elementiem, ir ērti aprēķināt pārvietojumus, izmantojot Vereshchagin metodi.

Piemēram, uzdevumam, kas attēlots attēlā. 47, reizinot diagrammas (48. att.), iegūstam kanoniskā vienādojuma koeficientus:

1 2 I 3 1 I / I 2 1 5 I1 3

E]L LL =-/ / -/ = -, E]A LR =-------- +-------.

1 11 2 3 3 1 1R 2 2 2 2 3 2/ 48 E]

gūt Chl - - = - E.

Spēka noteikšana X, mēs faktiski atradām atbalsta reakciju ES piedalos. Tālāk iekšējo spēka faktoru noteikšanas problēmu var atrisināt, kā parasti, izmantojot sekciju metodi.

KRIEVIJAS FEDERĀCIJAS IZGLĪTĪBAS MINISTRIJA

VALSTS IESTĀDE

KUZBAS VALSTS TEHNISKĀ UNIVERSITĀTE

Materiālu stiprības katedra

STATISTiski nenoteiktu eņģu stieņu SISTĒMU APRĒĶINS, ATTIECĪBĀ UZ SSPIEGOJUMU – SPIEDĒJUMU

Aprēķinu un grafiskā uzdevuma veikšanas vadlīnijas par materiālu stiprumu visu specialitāšu studentiem

Sastādījis: V.D. Moiseenko

Apstiprināts nodaļas sēdē Protokols Nr.8 29.06.01

Elektroniskā kopija atrodas KuzGTU galvenās ēkas bibliotēkā

Kemerova 2002

Ievads. Uzdevuma apjoms un mērķis

Statiski nenoteikta viru-stieņu sistēma ir tāda, kurā spēkus stieņos un reakcijas balstos nevar noteikt tikai no līdzsvara stāvokļa.

1. attēlā parādīts parasts kronšteins, kas sastāv no diviem stieņiem. Spēki N 1 un N 2 šīs kronšteina stieņos ir viegli nosakāmi no līdzsvara nosacījuma saplūstošo spēku sistēmai, kas pielikta izgrieztajam mezglam C, jo šai spēku sistēmai ir atrisināti divi vienādojumi ar diviem nezināmiem.

Ja kronšteina konstrukcija ir sarežģīta, pievienojot vēl vienu stieni (1. att., b), tad spēkus stieņos nevar noteikt tādā pašā veidā, jo mezglam C joprojām var sastādīt tikai divus statiskā līdzsvara vienādojumus (ΣХ). = 0; ΣY = 0), un nezināmo spēku skaits ir trīs. Mums kādreiz ir statiski nenoteikta sistēma.

Sarežģot konstrukciju un ieviešot jaunus stieņus, var iegūt statiski nenoteiktu sistēmu divas reizes (skat. 1.c att.), trīs reizes utt. Tāpēc ar statiski nenoteiktu sistēmu, kas mazāka par n reizēm, saprot tādu sistēmu, kurā savienojumu skaits pārsniedz statikas neatkarīgo vienādojumu skaitu par n vienībām.

Problēmas risināšanai nepieciešamos papildu vienādojumus var atrast, aplūkojot sistēmu deformētā stāvoklī un izveidojot saiknes starp konstrukcijas elementu nobīdēm un deformācijām. Iegūtos vienādojumus sauc par deformācijas saderības vienādojumiem.

2. attēlā parādītas dažu statiski nenoteiktu sistēmu diagrammas.

2. att. Dažu veidu statiski nenoteiktas sistēmas

Apgūstot sadaļu "Statiski nenoteiktas stieņu sistēmas" un veicot šo aprēķinu un grafisko uzdevumu, studentam jāapgūst statiski nenoteiktu sistēmu pazīmes; iegūt prasmes statiskās nenoteiktības atklāšanā, spēku noteikšanā konstrukcijas elementos un šķērsgriezuma laukumu izvēlē no stiprības nosacījuma.

Uzdevumā studentam jāveic šādas darbības:

- nosaka spēkus stieņos un izvēlas šķērsgriezuma laukumus no ārējo slodžu iedarbības;

- noteikt papildu spriegumus stieņos temperatūras izmaiņu dēļ;

- noteikt papildu stiprinājuma spriegumus, kas radušies stieņu ražošanas neprecizitātes dēļ;

- izvēlieties stieņu sekcijas atbilstoši robežstāvoklim.

Aprēķina un grafiskā uzdevuma izpildes apjoms un forma ir atkarīgi no apgūstamā kursa apjoma un to pārrunā pasniedzējs praktiskajās nodarbībās.

1. Īsa teorētiskā informācija

Risinot statiski nenoteiktas problēmas, jāievēro šāda secība:

1.1. Apsveriet problēmas statisko pusi. Izveidojiet spēku plānu un uzrakstiet statikas vienādojumus.

1.2. Apsveriet problēmas ģeometrisko pusi. Izveidojiet ceļojuma plānu. Sastādi papildu deformācijas saderības vienādojumus tādā daudzumā, lai varētu atrast visus nezināmos spēkus.

1.3. Apsveriet problēmas fizisko pusi. Saskaņā ar fizikas likumiem (ar temperatūras aprēķinu) un saskaņā ar Huka likumu, izsakiet deformācijas to saderības vienādojumos ar nezināmiem spēkiem, kas darbojas stieņos:

1.4. Izveidojiet kopīgu statikas, ģeometrijas, fizikas vienādojumu risinājumu un nosakiet nezināmos spēkus.

1.5. Izmantojot spiedes vai stiepes izturības apstākļus N/F = [ σ ], izvēlieties stieņu šķērsgriezuma laukumus.

1.6. Ar zināmiem spēkiem stieņos un pieņemtajiem šķērsgriezuma laukumiem aprēķiniet normālos spriegumus, izmantojot formulu

σ = N F .

2. Piemērs

Dots: Absolūti stingra sija AB balstās, kā parādīts 3. attēlā, noslogota ar vienmērīgi sadalītu slodzi un spēku P.

3. att. Statiski nenoteiktas sistēmas diagramma

Sākotnējie dati aprēķinam

4. Noteikt kopējos spriegumus stieņos no slodžu iedarbības, temperatūras izmaiņām un ražošanas neprecizitātēm.

2.1. Statiski nenoteiktas šarnīra stieņu sistēmas aprēķins ārējai slodzei

P = 30 kN q = 15 kN/m

A C B

4. att. Sākotnējā dizaina shēma

2.1.1. Problēmas statiskā puse

Problēmas statiskā puse tiek aplūkota spēku plānā. Spēka plāns ir projektēšanas shēma, kas parāda visus spēkus (gan zināmos, gan nezināmos), kas pielikti šarnīra stieņu sistēmas elementam, kura līdzsvars tiek ņemts vērā (mūsu gadījumā tas ir stingrs stars AB). Nogriezīsim tērauda un vara stieņus un nomainīsim to izmestās apakšējās daļas ar iekšējiem spēkiem (5. att.).

P = 30 kN q = 15 kN/m

A C B

60°

Rīsi. 5. Spēku plāns no ārējām slodzēm

No spēku plāna (skat. 5. att.) pierakstām statiskā līdzsvara vienādojumus. Lai atbildētu uz pirmo problēmas jautājumu, ir jāzina spēki stieņos - tērauds un varš. Šajā gadījumā nav jāaprēķina šarnīra balsta reakcija. Tātad no trim

iespējamos statikas vienādojumus (ΣX = 0; ΣY = 0 ; Σm c = 0 ) mēs rakstām

tāds, kas neietver pagrieziena fiksētā atbalsta reakcijas C:

∑ mC = 0

− N CT a + q a 2 2 + p a + NM sin60o b = 0,

- N ST 2 + 15 2 2 2 + 30 2 - NM 0,866 4 = 0,

Pēc algebriskām darbībām līdzsvara vienādojums iegūs formu

2.1.2. Problēmas ģeometriskā puse

Problēmas ģeometriskā puse tiek ņemta vērā pārvietošanas plānā. Pārvietojuma plāns ir dizaina diagramma, kas parāda šarnīra stieņu sistēmas stāvokli pirms un pēc iekraušanas. Pārvietojuma plānā mēs norādām sijas punktu nobīdes (AA1 un BB1),

vara un tērauda stieņu absolūtās deformācijas (∆ l ST ; ∆ l M )

(6. att.). Turklāt nelielu deformāciju dēļ mēs pārvietojam sijas punktus vertikāli uz augšu vai uz leju, un slīpo stieņu deformācijas atzīmējam ar perpendikulu.

Rīsi. 6. Noviržu plāns no ārējo slodžu iedarbības

Saskaņā ar pārvietošanas plānu mēs sastādam deformāciju savietojamības vienādojumu. Vispirms no trīsstūru AA1 C un CBB1 līdzības rakstām staru kūļa punktu nobīdes attiecību (6. att.):

Sijas punktu (AA1 un BB1) nobīdes ir izteiktas deformācijās

Izteiksmes (2.3) un (2.4) tiek aizstātas ar relāciju (2.2):

2.1.3. Problēmas fiziskā puse

Iegūto deformācijas saderības vienādojumu (2.5) šādā formā nevar atrisināt ar līdzsvara vienādojumu (2.1), jo tajos ietvertie nezināmie lielumi ir cita rakstura.

Absolūtās deformācijas ∆ l CT un ∆ l M vienādojumā (2.5) mēs izsakām

Mēs esam ieguvuši deformācijas saderības vienādojumu, kas uzrakstīts stieņos esošo spēku izteiksmē.

2.1.4. Sintēze

Kopīgi atrisināsim līdzsvara vienādojumus (2.1) un deformācijas saderības vienādojumu (2.6).

NCT + 1,73 NM = 45

0,67 NCT \u003d 0,95 NM.

No sistēmas otrā vienādojuma mēs izsakām spēku N ST:

un aizstājiet ar sistēmas pirmo vienādojumu.

N ST un N M pozitīvais rezultāts apstiprina mūsu pieņēmumus par tērauda stieņa saspiešanu un vara stieņa spriegumu, kas nozīmē, ka spēki stieņos būs:

2.1.5. Stieņu šķērsgriezumu izvēle

Stieņu šķērsgriezumu izvēle tiek veikta atbilstoši stiepes izturības stāvoklim - saspiešanai:

N F ≤ [σ] .

a) Tērauda stieņa šķērsgriezuma laukums, kas nepieciešams no stiprības stāvokļa, tiks noteikts:

b) No stiprības stāvokļa nepieciešamais vara stieņa šķērsgriezuma laukums tiks noteikts:

Šajā gadījumā saskaņā ar norādīto laukumu attiecību tērauda stieņa laukumam jābūt vienādam ar:

FCT = 4 3 FM = 4 3 1,7 10-4 = 1,275 10-4 m2 ..

Mēs pieņemam lielus stieņu šķērsgriezuma laukumus:

Ar pieņemtajiem vara un tērauda stieņu šķērsgriezuma laukumiem mēs nosakām spriegumus šajos stieņos.

2.2. Statiski nenoteiktas viras-stieņa sistēmas temperatūras aprēķins

Temperatūras aprēķina mērķis ir noteikt papildu spriegumus vara un tērauda stieņos temperatūras izmaiņu dēļ.

Pieņemsim, ka sistēma tiek uzkarsēta par ∆ t = 20 o C. Risinājuma algoritms paliek nemainīgs. Sākotnējā dizaina shēma ir parādīta attēlā. 7.

Tiek sauktas stieņu sistēmas, kurās atbalsta reakcijas un iekšējo spēku faktorus nevar atrast tikai no līdzsvara vienādojumiem statiski nenoteikts.

Nosaka starpību starp nepieciešamo nezināmo spēku skaitu un neatkarīgiem līdzsvara vienādojumiem sistēmas statiskās nenoteiktības pakāpe. Statiskās nenoteiktības pakāpe vienmēr ir vienāda ar lieko (lieko) savienojumu skaitu, kuru noņemšana pārvērš statiski nenoteiktu sistēmu par statiski nosakāmu ģeometriski nemainīgu sistēmu. Gan ārējie (atsauces) savienojumi, gan iekšējie, kas uzliek noteiktus ierobežojumus sistēmas sekciju kustībai attiecībā pret otru, var būt lieki.

Ģeometriski nemainīgs sauc tādu sistēmu, kuras formas maiņa iespējama tikai saistībā ar tās elementu deformācijām.

Ģeometriski mainīgs sauc tādu sistēmu, kuras elementi ārējo spēku iedarbībā var kustēties bez deformācijas (mehānisms).

Attēlā parādīts. 12.1 rāmim ir septiņas ārējās (atbalsta) saites. Lai noteiktu spēkus šajās saitēs (atbalsta reakcijas), ir iespējams sastādīt tikai trīs neatkarīgus līdzsvara vienādojumus. Tāpēc šai sistēmai ir četri lieki savienojumi, kas nozīmē, ka tā ir četras reizes statiski nenoteikta. Tādējādi plakano rāmju statiskās nenoteiktības pakāpe ir:

Kur R- atbalsta reakciju skaits.

Kontūru, kas sastāv no vairākiem elementiem (taisniem vai izliektiem), kas ir stingri (bez eņģēm) savienoti viens ar otru un veido slēgtu ķēdi, sauc par slēgtu ķēdi. . 12.2. attēlā parādītais taisnstūra rāmis ir slēgta cilpa. Tas ir trīs reizes statiski nenoteikts, jo, lai to padarītu statiski nenoteiktu, ir nepieciešams nogriezt vienu no tā elementiem un likvidēt trīs papildu savienojumus. Šo saišu reakcijas ir: gareniskais spēks, šķērsspēks un lieces moments, kas iedarbojas griešanas punktā; tos nevar noteikt, izmantojot statikas vienādojumus. Līdzīgos apstākļos statiskās nenoteiktības izpratnē pastāv jebkura slēgta cilpa, kas ir vienmēr trīs reizes statiski nenoteikts.

Eņģes iekļaušana rāmja mezglā, kurā saplūst divi stieņi, vai novietošana jebkurā vietā uz stieņa ass noņem vienu savienojumu un samazina kopējo statiskās nenoteiktības pakāpi par vienu. Šādu viru sauc par vienu vai vienkāršu (12.3. att.).

Kopumā katra vira ir iekļauta savienojuma mezglā c stieņi, samazina statiskās nenoteiktības pakāpi par c-1 , jo šāda vira aizstāj c-1 vienas eņģes (12.3. att.). Tādējādi sistēmas statiskās nenoteiktības pakāpi slēgtu cilpu klātbūtnē nosaka pēc formulas.

Šādu sistēmu sauc par statiski nenoteiktu, ja to nevar aprēķināt, izmantojot tikai statikas vienādojumus, jo tai ir nevajadzīgi savienojumi. Lai aprēķinātu šādas sistēmas, tiek sastādīti papildu vienādojumi, kas ņem vērā sistēmas deformācijas.

Statiski nenoteiktas sistēmas ir vairākas raksturīgas iezīmes:

1. statiski nenoteikts struktūras ir stingrākas nekā atbilstošās statiski noteikts, jo tiem ir papildu savienojumi.
2. Iekš statiski nenoteikts sistēmām, ir mazāki iekšējie spēki, kas nosaka to efektivitāti salīdzinājumā ar statiski noteikts sistēmas zem vienādām ārējām slodzēm.
3. Nevajadzīgu savienojumu pārkāpšana iekšā statiski nenoteikts sistēma ne vienmēr noved pie iznīcināšanas, savukārt sakaru zudums statiski noteikts sistēma padara to ģeometriski mainīgu.
4. Aprēķiniem statiski nenoteikts sistēmām, ir nepieciešams provizoriski precizēt elementu šķērsgriezumu ģeometriskos raksturlielumus, t.i. patiesībā to forma un izmērs, jo to maiņa izraisa savienojumu spēku izmaiņas un jaunu centienu sadalījumu visos sistēmas elementos.
5. Aprēķinot statiski nenoteikts sistēmām, ir nepieciešams iepriekš izvēlēties konstrukcijas materiālu, jo ir jāzina tā elastības moduļi.
6. Iekš statiski nenoteikts sistēmas, temperatūras ietekme, balstu nosēšanās, ražošanas un uzstādīšanas neprecizitātes rada papildu pūles.

Galvenā aprēķinu metodesstatiski nenoteikts sistēmas ir:

1. spēka metode. Šeit spēki tiek uzskatīti par nezināmiem – spēkiem un momentiem.
2.Kustības metode. Nezināmi ir deformācijas faktori – griešanās leņķi un lineārās nobīdes.
3.jaukta metode.Šeit daļa nezināmo apzīmē centienus, bet otra daļa - pārvietošanos.
4. Kombinētā metode. To izmanto asimetrisko slodžu simetrisko sistēmu aprēķināšanā. Izrādās, ka sistēmu ieteicams aprēķināt noteiktas slodzes simetriskajai sastāvdaļai ar nobīdes metodi, bet apgriezti simetriskajai komponentei - ar spēka metodi.
Papildus norādītajām analītiskajām metodēm īpaši sarežģītu sistēmu aprēķinos tiek izmantotas dažādas skaitliskās metodes.

Spēka metodes kanoniskie vienādojumi

Lai iegūtu papildu vienādojumus, kas tika minēti iepriekšējā rindkopā, vispirms ir jāpagriež dotais n reizes statiski nenoteikts sistēmu par statiski noteiktu, noņemot no tās nevajadzīgos savienojumus. Iegūto statiski determinēto sistēmu sauc pamata.Ņemiet vērā, ka dotās sistēmas pārveidošana par statiski noteiktu sistēmu nav obligāta. Dažreiz tiek izmantota spēka metodes modifikācija, kurā var būt pamatā esošā sistēma statiski nenoteikts tomēr šīs problēmas izklāsts ir ārpus šīs rokasgrāmatas darbības jomas. Jebkuru saišu likvidēšana nemaina sistēmas iekšējos spēkus un deformācijas, ja tai tiek pielikti papildu spēki un momenti, kas ir izmesto saišu reakcijas. Tas nozīmē, ka, ja galvenajai sistēmai tiek piemērota noteikta slodze un attālo saišu reakcijas, tad galvenā un dotā sistēma kļūs ekvivalents.

Dotajā sistēmā nevar būt pārvietošanās pa esošo stingro saišu virzieniem, ieskaitot tās saites, kuras tiek izmestas, pārejot uz galveno sistēmu, tāpēc galvenajā sistēmā pārvietojumiem pa izmesto saišu virzieniem ir jābūt būt vienāds ar nulli. Un šim nolūkam nokritušo saišu reakcijām ir jābūt stingri noteiktām vērtībām.

Nosacījumam par nobīdes vienādību ar nulli jebkura i-tā savienojuma virzienā no n, kas atmests, pamatojoties uz spēku darbības neatkarības principu, ir šāda forma:

kur pirmais rādītājs norāda kustības virzienu un pārtrauktā savienojuma numuru, bet otrais norāda iemeslu, kas izraisīja kustību, t.i. ir kustība i-tās saites virzienā, ko izraisa k-tās saites reakcija; - kustība i-tā savienojuma virzienā, ko izraisa visas ārējās slodzes vienlaicīga darbība.

Spēka metodē k-tās saites reakciju parasti apzīmē ar Xk. Ņemot vērā šo apzīmējumu un Huka likuma spēkā esamību, pārvietojumus var attēlot kā:

kur ir viena (vai specifiska) kustība i-tās saites virzienā, ko izraisa reakcija t.i. reakcija sakrīt virzienā ar Xk, bet vienāda ar vienotību.

Aizstājot (2) ar (1), mēs iegūstam:

fiziskā nozīme vienādojums (3): kustība galvenajā sistēmā i-tā izmestā savienojuma virzienā ir vienāda ar nulli.

Rakstot izteiksmes, kas līdzīgas (3) visai atmesto saišu kopai, mēs iegūstam kanonisko vienādojumu sistēmaspēka metode:

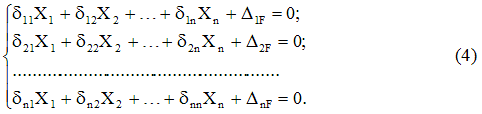
(4) vienādojuma forma, t.i. terminu skaitu katrā no tiem un to kopējo skaitu nosaka tikai sistēmas statiskās nenoteiktības pakāpe un tas nav atkarīgs no tās specifiskajām iezīmēm.

Kanonisko vienādojumu sistēmas (4) koeficientus nosaka ar Mohr-Vereshchagin metodi, reizinot atbilstošās diagrammas. Visi šie koeficienti, kā minēts iepriekš, atspoguļo pārvietojumus; koeficienti, kas stāv pie nezināmajiem, ir vienību pārvietojumi, un brīvie locekļi ir kravas. Atsevišķas kustības ir sadalītas galvenais, atrodas gar galveno diagonāli un kuriem ir vienādi indeksi un blakus efekti(). Galvenās kustības vienmēr ir pozitīvas, atšķirībā no sānu kustībām. Simetriski izvietoti pārvietojumi, saskaņā ar teorēmu par pārvietojumu savstarpīgumu, ir vienādi viens ar otru, t.i. .

Spēka metodes aprēķināšanas algoritms

Neatkarīgi no aplūkotās konstrukcijas iezīmēm var izdalīt šādu statiski nenoteiktu sistēmu aprēķinu secību spēka metode:

1. Nosakiet statiskās nenoteiktības pakāpe.
2. Izvēlieties galveno sistēmu.
3. Izveidojiet līdzvērtīgu sistēmu.
4. Sadedzināt sistēmu kanoniskie vienādojumi.
5. Konstruēt aplūkojamās konstrukcijas elementos radušos iekšējo spēku faktoru vienību un slodžu diagrammas.
6. Aprēķināt kanonisko vienādojumu sistēmas nezināmo un brīvo terminu koeficientus.
7. Izveidojiet kopējo vienotu diagrammu.
8. Veikt universālu koeficientu pārbaudi nezināmiem un brīviem terminiem.
9. Atrisināt sistēmu (4), t.i. noteikt papildu saišu reakcijas.
10. Konstruēt dotās sistēmas topošo iekšējo spēku faktoru diagrammas (citiem vārdiem sakot, galīgās diagrammas).
11. Veikt statiskās un kinemātiskās pārbaudes.
Ņemiet vērā, ka iepriekšminētā algoritma 7., 8., 11. punkti nav absolūti nepieciešami, lai gan tie ļauj kontrolēt aprēķina pareizību. Un sistēmām ar vienu papildu savienojumu 7. un 8. punkts ir vienkārši bezjēdzīgi, jo šajā gadījumā kopējā diagramma sakrīt ar vienu.
Sīkāk apskatīsim dažas no iepriekš minētajām aprēķina darbībām.

Primārās sistēmas izvēle

Šis ir vissvarīgākais aprēķina posms, jo racionāla galvenās sistēmas izvēle ievērojami vienkāršo skaitļošanas darbu. Apsvērsim iespējamos veidus, kā noņemt nevajadzīgus savienojumus, kas nosaka galvenās sistēmas formu.

1. Nevajadzīgo savienojumu noraidīšana tiek veikta, pilnībā noņemot dažus balstus vai nomainot tos ar balstiem ar mazāku savienojumu skaitu. Reakcijas, kas iedarbojas pamesto saišu virzienos, ir lieki nezināmie. Attēlā 1, b, c, d parādītas dažādas līdzvērtīgas sistēmas versijas, kas iegūtas ar šo metodi rāmim (1. att., a).

2. Eņģu izvietojums stieņu starpsekcijās ļauj katrā šādā sekcijā izveidot savienojumu, kas atbilst lieces momentam. Šie brīži ir lieki nezināmie. Rāmim ar statiskās nenoteiktības pakāpi n = 3 (2. att., a), izvēloties galveno sistēmu, jāuzstāda trīs eņģes. Šo eņģu novietojums var būt patvaļīgs, bet apmierinot sistēmas ģeometriskās nemainīguma prasību (2.b att.).

3. Stieņa sadalīšana novērš trīs saites, kas atbilst iekšējiem spēkiem M, Q, N (2. att., c). Atsevišķos gadījumos (2.d att.), griežot stieni gar viru, tiek atbrīvotas divas saites (2. att., e), un, nogriežot taisnu stieni ar eņģēm galos, tiek atbrīvota viena saite (2. att., f).

Starp statiski nenoteiktas sistēmas savienojumiem izšķir absolūti nepieciešamos un nosacīti nepieciešamos. Absolūti nepieciešamas ir saites, kuras noņemot, sistēma kļūst ģeometriski maināma. Absolūti nepieciešamu savienojumu raksturo piepūles statiskā nosakāmība tajā, t.i. šādas saites reakciju var aprēķināt no līdzsvara stāvokļa. Izvēloties galveno sistēmu, nevar izmest absolūti nepieciešamos savienojumus.

Attiecības, kuru noņemšanas gadījumā sistēma turpina palikt ģeometriski nemainīga, sauc par nosacīti nepieciešamām. Sistēma, kas ir atsaistīta, var būt primārā sistēma spēka metode.

Kanonisko vienādojumu koeficientu un brīvo terminu aprēķināšana

Pirms šī aprēķina posma tiek sastādītas iekšējo spēka faktoru vienības un slodzes diagrammas (sijām un rāmjiem - lieces momentu diagrammas). Mērvienību diagrammas tiek konstruētas no bezizmēra vienības spēka vai bezizmēra vienības momenta darbības, kas sakrīt virzienā ar atbilstošā nezināmā pārpalikuma virzienu ekvivalentajā sistēmā, un tiek apzīmētas ar , bet mērvienību diagramma - ar .

Slodzes diagramma ir veidota no ārējās slodzes, kas tiek pielietota galvenajai sistēmai. Šajā gadījumā jūs varat izveidot vienu diagrammu no visu ārējo slodžu vienlaicīgas darbības vai vairākas diagrammas, atsevišķi no katras pielietotās slodzes. Šāda vienas slodzes diagrammas sadalīšana vairākās vienkāršākos, kā likums, ir ieteicama tikai tad, ja starp esošajām slodzēm ir vienmērīgi sadalīta, un momentu diagramma attiecīgajā sadaļā zem tās ir mainīga. Šajā gadījumā katrā kanoniskajā vienādojumā brīvo terminu skaits būs vienāds ar uzzīmēto slodzes diagrammu skaitu.

Vienību un slodzes pārvietojumus (kanonisko vienādojumu koeficientus un brīvos nosacījumus) parasti var aprēķināt ar Mora metodi. Sijām un rāmjiem to var izdarīt, izmantojot Vereshchagin likumu.

Universāla kanonisko vienādojumu koeficientu un brīvo terminu pārbaude

Lai veiktu universālu pārbaudi, ir nepieciešams izveidot kopējo vienību diagrammu - momentu diagrammu no visu galvenajai sistēmai pielietoto vienības spēku vienlaicīgas darbības:

Mēs reizinām kopējo diagrammu ar diagrammu:

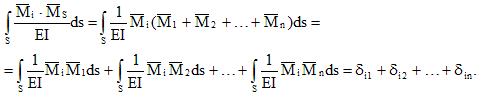
Tādējādi kopsummas un i-tās vienotās diagrammas reizināšanas rezultāts ir kustība i-tā savienojuma virzienā no atsevišķu papildu nezināmo kopīgās darbības. Šī nobīde ir vienāda ar i-tā kanoniskā vienādojuma koeficientu summu:

Šo pārbaudi sauc rinda pēc rindas un attiecas uz katru kanonisko vienādojumu.
n rindu pārbaužu vietā visbiežāk tiek veikta viena - universāls čeks, kas sastāv no kopējās vienības diagrammas reizināšanas un stāvokļa pārbaudes:

Ja tiek veikta universālā pārbaude, tad vienības pārvietojumi tiek aprēķināti pareizi; ja nē, nepieciešams veikt pārbaudes pa rindiņām, kas ļaus noskaidrot pārvietojumu, kura aprēķinā tika pieļauta kļūda.

Lai pārbaudītu slodzes pārvietojumus, jāreizina lieces momentu kopējās vienības un slodzes diagrammas:

Tādējādi kanonisko vienādojumu sistēmas (4) brīvo nosacījumu pārbaude sastāv no nosacījuma izpildes.