ფუნქციის კონცეფცია, ფუნქციის თვისებები, ფუნქციების გრაფიკა. ფუნქციების ძირითადი ცნებები და თვისებები

ფუნქციები და მათი თვისებები

ფუნქცია ერთ-ერთი ყველაზე მნიშვნელოვანი მათემატიკური ცნებაა.ფუნქცია ისინი უწოდებენ y ცვლადის ასეთ დამოკიდებულებას x ცვლადზე, რომელშიც x ცვლადის თითოეული მნიშვნელობა შეესაბამება y ცვლადის ერთ მნიშვნელობას.

ცვლადი Xდაურეკა დამოუკიდებელი ცვლადი ან არგუმენტი.ცვლადი ზედაურეკა დამოკიდებული ცვლადი. ამასაც ამბობენცვლადი y არის x ცვლადის ფუნქცია. დამოკიდებული ცვლადის მნიშვნელობებს უწოდებენფუნქციის მნიშვნელობები.

თუ ცვლადის დამოკიდებულებაზე ცვლადიდანX არის ფუნქცია, მაშინ ის შეიძლება მოკლედ დაიწეროს შემდეგნაირად:წ= ვ( x ). (წაიკითხეთ:ზე უდრისვ საწყისიX .) სიმბოლოვ( x) აღვნიშნო ფუნქციის მნიშვნელობა, რომელიც შეესაბამება არგუმენტის მნიშვნელობას ტოლიX .

დამოუკიდებელი ცვლადის ფორმის ყველა მნიშვნელობაფუნქციის დომენი . ყველა მნიშვნელობა, რომელსაც იღებს დამოკიდებული ცვლადიფუნქციის დიაპაზონი .

თუ ფუნქცია მითითებულია ფორმულით და მისი განმარტების დომენი არ არის მითითებული, მაშინ ფუნქციის განსაზღვრის დომენი ითვლება არგუმენტის ყველა მნიშვნელობისგან, რომლისთვისაც ფორმულა აზრი აქვს.

ფუნქციის მითითების მეთოდები:

1.ანალიტიკური მეთოდი (ფუნქცია მითითებულია გამოყენებით მათემატიკური ფორმულა;

2.ტაბულური მეთოდი (ფუნქცია მითითებულია ცხრილის გამოყენებით)

3.აღწერითი მეთოდი (ფუნქცია მითითებულია სიტყვიერი აღწერა)

4. გრაფიკული მეთოდი (ფუნქცია მითითებულია გრაფიკის გამოყენებით).

ფუნქციის გრაფიკი დაასახელეთ კოორდინატთა სიბრტყის ყველა წერტილის სიმრავლე, რომელთა აბსციები უდრის არგუმენტის მნიშვნელობებს და ორდინატებს - შესაბამისი ფუნქციის მნიშვნელობები.

ფუნქციების ძირითადი თვისებები

1. ფუნქცია ნულები

ფუნქციის ნული არის არგუმენტის მნიშვნელობა, რომლის დროსაც ფუნქციის მნიშვნელობა ნულის ტოლია.

2. ფუნქციის მუდმივი ნიშნის ინტერვალები

ფუნქციის მუდმივი ნიშნის ინტერვალები არის არგუმენტების მნიშვნელობების ნაკრები, რომლებზეც ფუნქციის მნიშვნელობები მხოლოდ დადებითი ან მხოლოდ უარყოფითია.

3. გაზრდის (შემცირების) ფუნქცია.

მზარდი რაღაც ინტერვალში ფუნქცია არის ფუნქცია, რომლისთვისაც უფრო მაღალი ღირებულებაარგუმენტი ამ ინტერვალიდან შეესაბამება ფუნქციის უფრო დიდ მნიშვნელობას.

ფუნქცია y = ვ ( x ) დაურეკა იზრდება ინტერვალზე (ა; ბ ), თუ რომელიმესთვის x 1 და x 2 ამ ინტერვალიდან ისეთი რომx 1 < x 2 , უთანასწორობა მართალიავ ( x 1 )< ვ ( x 2 ).

Დაღმავალი გარკვეულ ინტერვალში ფუნქცია არის ფუნქცია, რომელშიც არგუმენტის უფრო დიდი მნიშვნელობა ამ ინტერვალიდან შეესაბამება ფუნქციის უფრო მცირე მნიშვნელობას.

ფუნქცია ზე = ვ ( x ) დაურეკა მცირდებაინტერვალზე (ა; ბ ) , თუ რომელიმესთვის x 1 და x 2 ამ ინტერვალიდან ისეთი რომ x 1 < x 2 , უთანასწორობა მართალიავ ( x 1 )> ვ ( x 2 ).

4. ლუწი (კენტი) ფუნქცია

თუნდაც ფუნქცია - ფუნქცია, რომლის განსაზღვრის დომენი სიმეტრიულია კოორდინატების წარმოშობის მიმართ და ნებისმიერისთვისX განმარტების სფეროდან თანასწორობავ (- x ) = ვ ( x ) . ლუწი ფუნქციის გრაფიკი სიმეტრიულია ორდინატთან მიმართებაში.

მაგალითად, y = x 2 - თუნდაც ფუნქცია.

უცნაური ფუნქცია- ფუნქცია, რომლის განსაზღვრის დომენი სიმეტრიულია კოორდინატების წარმოშობის მიმართ და ნებისმიერისთვის Xგანმარტების სფეროდან თანასწორობა მართალია ვ (- x ) = - ვ (x ). კენტი ფუნქციის გრაფიკი სიმეტრიულია წარმოშობის მიმართ.

მაგალითად: y = x 3 - უცნაური ფუნქცია .

ფუნქცია ზოგადი ხედიარ არის ლუწი ან კენტი (y = x 2 +x ).

ზოგიერთი ფუნქციის თვისებები და მათი გრაფიკა

1. ხაზოვანი ფუნქცია ფორმის ფუნქციას უწოდებენ , სად კ და ბ - ნომრები.

წრფივი ფუნქციის განსაზღვრის დომენი არის სიმრავლერ რეალური რიცხვები.

წრფივი ფუნქციის გრაფიკიზე = kx + ბ ( კ ≠ 0) არის სწორი ხაზი, რომელიც გადის წერტილში (0;ბ ) და ხაზის პარალელურადზე = kx .

სწორი, არა ღერძის პარალელურადOU, არის წრფივი ფუნქციის გრაფიკი.

წრფივი ფუნქციის თვისებები.

1. როცა კ > 0 ფუნქცია ზე = kx + ბ

2. როცა კ < 0 ფუნქცია y = kx + ბ მცირდება განმარტების სფეროში.

წ = kx + ბ ( კ ≠ 0 ) არის მთელი რიცხვითი წრფე, ე.ი. რამოდენიმერ რეალური რიცხვები.

ზე კ = 0 ფუნქციის მნიშვნელობების ნაკრებიy = kx + ბ შედგება ერთი ნომრისგანბ .

3. როცა ბ = 0 და კ = 0 ფუნქცია არც ლუწია და არც კენტი.

ზე კ = 0 ხაზოვანი ფუნქციაროგორც ჩანსy = ბ და ზე ბ ≠ 0 ეს არის თანაბარი.

ზე კ = 0 და ბ = 0 წრფივ ფუნქციას აქვს ფორმაy = 0 და არის ლუწიც და კენტიც.

წრფივი ფუნქციის გრაფიკიy = ბ არის სწორი ხაზი, რომელიც გადის წერტილში (0; ბ ) და ღერძის პარალელურადოჰ.გაითვალისწინეთ, რომ როდესაც ბ = 0 ფუნქციის გრაფიკიy = ბ ემთხვევა ღერძს ოჰ .

5. როცა კ > 0 ჩვენ გვაქვს ეს ზე> 0 თუ და ზე< 0 თუ. ზე კ < 0 გვაქვს, რომ y > 0 თუდა ზე< 0, если .

2. ფუნქცია წ = x 2

რრეალური რიცხვები.

ცვლადის მიცემაX რამდენიმე მნიშვნელობა ფუნქციის დომენიდან და შესაბამისი მნიშვნელობების გამოთვლაზეფორმულის მიხედვით წ = x 2 , ჩვენ გამოვსახავთ ფუნქციის გრაფიკს.

ფუნქციის გრაფიკი წ = x 2 დაურეკა პარაბოლა.

y = x ფუნქციის თვისებები 2 .

1. თუ X= 0, მაშინ y = 0, ე.ი. პარაბოლას აქვს საკოორდინატო ღერძი საერთო წერტილი(0; 0) - წარმოშობა.

2. თუ x ≠ 0 , რომ ზე > 0, ე.ი. პარაბოლის ყველა წერტილი, გარდა საწყისისა, მდებარეობს x ღერძის ზემოთ.

3. ფუნქციის მნიშვნელობების ნაკრებიზე = X 2 არის span ფუნქციაზე = X 2 მცირდება.

X

3.ფუნქცია

ამ ფუნქციის დომენი არის span ფუნქციაწ = | x | მცირდება.

7. ყველაზე დაბალი ღირებულებაფუნქცია იღებს წერტილსX,ის უდრის 0. უდიდესი ღირებულებაარ არსებობს.

6. ფუნქცია

ფუნქციის ფარგლები: .

ფუნქციის დიაპაზონი: .

გრაფიკი არის ჰიპერბოლა.

1. ფუნქცია ნულები.

y ≠ 0, ნულის გარეშე.

2. ნიშნების მუდმივობის ინტერვალები,

თუ კ > 0, მაშინ ზე> 0 საათზე X > 0; ზე < 0 при X < О.

თუ კ < 0, то ზე < 0 при X > 0; ზე> 0 საათზე X < 0.

3. მატებისა და შემცირების ინტერვალები.

თუ კ > 0, მაშინ ფუნქცია მცირდება როგორც .

თუ კ < 0, то функция возрастает при .

4. ლუწი (კენტი) ფუნქცია.

ფუნქცია უცნაურია.

კვადრატული ტრინომიალი

ფორმის განტოლება ნაჯახი 2 + bx + გ = 0, სადაც ა , ბდა თან - რამდენიმე რიცხვი დაa≠ 0, დარეკა კვადრატი.

კვადრატულ განტოლებაშინაჯახი 2 + bx + გ = 0 კოეფიციენტი ადაურეკა პირველი კოეფიციენტი ბ - მეორე კოეფიციენტებით - თავისუფალი წევრი.

ფესვის ფორმულა კვადრატული განტოლებააქვს ფორმა:

.

გამოთქმა ე.წ დისკრიმინანტი კვადრატული განტოლება და აღინიშნებად .

თუ დ = 0, მაშინ არის მხოლოდ ერთი რიცხვი, რომელიც აკმაყოფილებს განტოლებას ნაჯახი 2 + bx + გ = 0. თუმცა, ჩვენ შევთანხმდით იმის თქმაზე, რომ ამ შემთხვევაში კვადრატულ განტოლებას აქვს ორი თანაბარი რეალური ფესვი და თავად რიცხვი დაურეკა ორმაგი ფესვი.

თუ დ < 0, то квадратное уравнение не имеет действительных корней.

თუ დ > 0, მაშინ კვადრატულ განტოლებას აქვს ორი განსხვავებული ნამდვილი ფესვები.

მიეცით კვადრატული განტოლებანაჯახი 2 + bx + გ = 0. ვინაიდან a≠ 0, შემდეგ ორივე ნაწილის გაყოფა მოცემული განტოლება onA, ვიღებთ განტოლებას . სჯეროდა და , მივდივართ განტოლებამდე , რომელშიც პირველი კოეფიციენტი უდრის 1. ასეთი განტოლება ე.წმოცემული.

ზემოაღნიშნული კვადრატული განტოლების ფესვების ფორმულა არის:

.

ფორმის განტოლებები

ა x 2 + bx = 0, ნაჯახი 2 + ს = 0, ა x 2 = 0

უწოდებენ არასრული კვადრატული განტოლებები. არასრული კვადრატული განტოლებები იხსნება განტოლების მარცხენა მხარის ფაქტორინგით.

ვიეტას თეორემა .

კვადრატული განტოლების ფესვების ჯამი უდრის მეორე კოეფიციენტის შეფარდებას პირველთან, აღებული საპირისპირო ნიშნით, ხოლო ფესვების ნამრავლი არის თავისუფალი წევრის შეფარდება პირველ კოეფიციენტთან, ე.ი.

ურთიერთობის თეორემა.

თუ რომელიმე ორი რიცხვის ჯამიX 1 და X 2 ტოლია და მათი პროდუქტი ტოლია, მაშინ ეს რიცხვები კვადრატული განტოლების ფესვებიაოჰ 2 + ბ x + c = 0.

ფორმის ფუნქცია ოჰ 2 + ბ x + cდაურეკა კვადრატული ტრინომიალი. ამ ფუნქციის ფესვები არის შესაბამისი კვადრატული განტოლების ფესვებიოჰ 2 + ბ x + c = 0.

თუ დისკრიმინანტი კვადრატული ტრინომიალიარის ნულზე მეტი, მაშინ ეს ტრინომი შეიძლება წარმოდგენილი იყოს როგორც:

ოჰ 2 + ბ x + c = a(x-x 1 ) (x-x 2 )

სად X 1 და X 2 - ტრინომის ფესვები

თუ კვადრატული ტრინომის დისკრიმინანტი ნულის ტოლი, მაშინ ეს ტრინომი შეიძლება წარმოდგენილი იყოს როგორც:

ოჰ 2 + ბ x + c = a(x-x 1 ) 2

სად X 1 - ტრინომის ფესვი.

Მაგალითად, 3x 2 - 12x + 12 = 3 (x - 2) 2 .

ფორმის განტოლება ოჰ 4 + ბ X 2 + ს= 0 ეწოდება ბიკვადრატული. ცვლადის ჩანაცვლების გამოყენება ფორმულის გამოყენებითX 2 = წ იგი მცირდება კვადრატულ განტოლებამდეა წ 2 + მიერ + s = 0.

კვადრატული ფუნქცია

კვადრატული ფუნქცია არის ფუნქცია, რომელიც შეიძლება დაიწეროს ფორმის ფორმულითწ = ნაჯახი 2 + bx + გ , სად x - დამოუკიდებელი ცვლადი,ა , ბ და გ - რამდენიმე რიცხვი დაა ≠ 0.

ფუნქციის თვისებები და მისი გრაფიკის ტიპი განისაზღვრება ძირითადად კოეფიციენტის მნიშვნელობებითა და დისკრიმინაციული.

კვადრატული ფუნქციის თვისებები

დომენი:რ;

მნიშვნელობების დიაპაზონი:

ზე ა > 0 [- დ/(4 ა); ∞)

ზე ა < 0 (-∞; - დ/(4 ა)];

ლუწი, კენტი:

ზე ბ = 0 ლუწი ფუნქცია

ზე ბ ≠ 0 ფუნქცია არც ლუწია და არც კენტი

ზე დ> 0 ორი ნული: ,

ზე დ= 0 ერთი ნული:

ზე დ < 0 нулей нет

მონიშნეთ მუდმივობის ინტერვალები:

თუ a > 0, დ> 0, მაშინ

თუ a > 0, დ= 0, მაშინ

ეთუ a > 0, დ < 0, то

თუ< 0, დ> 0, მაშინ

თუ< 0, დ= 0, მაშინ

თუ< 0, დ < 0, то

- ერთფეროვნების ინტერვალები

> 0-ისთვის

ზე ა< 0

კვადრატული ფუნქციის გრაფიკი არისპარაბოლა - სიმეტრიული მრუდი სწორი ხაზის მიმართ , პარაბოლის წვეროზე გავლისას (პარაბოლის წვერო არის პარაბოლის გადაკვეთის წერტილი სიმეტრიის ღერძთან).

კვადრატული ფუნქციის გრაფიკისთვის საჭიროა:

1) იპოვეთ პარაბოლის წვეროს კოორდინატები და მონიშნეთ იგი კოორდინატულ სიბრტყეში;

2) ააგეთ პარაბოლას კუთვნილი კიდევ რამდენიმე წერტილი;

3) შეაერთეთ მონიშნული წერტილები გლუვი ხაზით.

პარაბოლის წვეროს კოორდინატები განისაზღვრება ფორმულებით:

; .

ფუნქციის გრაფიკების კონვერტაცია

1. გაჭიმვა გრაფიკული ხელოვნებაy = x 2 ღერძის გასწვრივზე ვ|ა| ჯერ (ზე|ა| < 1 არის შეკუმშვა 1/|ა| ერთხელ).

თუ და< 0, произвести, кроме того, სარკის ანარეკლიგრაფიკა ღერძის შესახებX (პარაბოლას ტოტები მიმართული იქნება ქვემოთ).

შედეგი: ფუნქციის გრაფიკიy = აჰ 2 .

2. პარალელური გადაცემა ფუნქციური გრაფიკაy = აჰ 2 ღერძის გასწვრივX on| მ | (მარჯვნივ, როცა

მ > 0 და მარცხნივ, როდესაცთ< 0).

შედეგი: ფუნქციის გრაფიკიy = a(x - t) 2 .

3. პარალელური გადაცემა ფუნქციური გრაფიკა ღერძის გასწვრივზე on| ნ | (ზევითp> 0 და ქვემოთპ< 0).

შედეგი: ფუნქციის გრაფიკიy = a(x - t) 2 + გვ.

კვადრატული უტოლობები

ფორმის უტოლობებიოჰ 2 + ბ x + c > 0 დაოჰ 2 + bx + c< 0, სადაცX - ცვლადი,ა , ბ დათან - რამდენიმე რიცხვი დაa≠ 0 ეწოდება მეორე ხარისხის უტოლობებს ერთი ცვლადით.

მეორე ხარისხის უტოლობის ამოხსნა ერთ ცვლადში შეიძლება ჩაითვალოს როგორც იმ ინტერვალების პოვნა, რომლებშიც შესაბამისი კვადრატული ფუნქცია იღებს დადებით ან უარყოფით მნიშვნელობებს.

ფორმის უტოლობების ამოხსნაოჰ 2 + bx + c > 0 დაოჰ 2 + bx + c< 0 გააგრძელეთ შემდეგნაირად:

1) იპოვეთ კვადრატული სამწევრის დისკრიმინანტი და გაარკვიეთ აქვს თუ არა ტრინომს ფესვები;

2) თუ ტრინომს აქვს ფესვები, მაშინ მონიშნეთ ისინი ღერძზეX და მონიშნული წერტილების მეშვეობით სქემატურად იხატება პარაბოლა, რომლის ტოტები მიმართულია ზემოთ.ა > 0 ან ქვემოთ, როდესაცა< 0; თუ ტრინომს არ აქვს ფესვები, მაშინ სქემატურად გამოსახეთ პარაბოლა, რომელიც მდებარეობს ზედა ნახევარ სიბრტყეშია > 0 ან უფრო დაბალი atა < 0;

3) ნაპოვნია ღერძზეX ინტერვალები, რომლებისთვისაც პარაბოლის წერტილები განლაგებულია ღერძის ზემოთX (თუ უთანასწორობა მოგვარებულიაოჰ 2 + bx + c > 0) ან ღერძის ქვემოთX (თუ უთანასწორობა მოგვარებულიაოჰ 2 + bx + c < 0).

მაგალითი:

მოვაგვაროთ უტოლობა .

განიხილეთ ფუნქცია

მისი გრაფიკი არის პარაბოლა, რომლის ტოტები მიმართულია ქვემოთ (რადგან ).

მოდით გავარკვიოთ, როგორ მდებარეობს გრაფიკი ღერძის მიმართX. მოდით ამოვხსნათ განტოლება . ჩვენ ამას მივიღებთx = 4. განტოლებას აქვს ერთი ფესვი. ეს ნიშნავს, რომ პარაბოლა ეხება ღერძსX.

პარაბოლის სქემატურად გამოსახვით ვხვდებით, რომ ფუნქცია ნებისმიერს უარყოფით მნიშვნელობებს იღებსX, გარდა 4.

პასუხი შეიძლება დაიწეროს ასე:X - ნებისმიერი რიცხვი, რომელიც არ არის 4-ის ტოლი.

უტოლობების ამოხსნა ინტერვალის მეთოდით

გადაწყვეტის დიაგრამა

1. იპოვე ნულები ფუნქცია უტოლობის მარცხენა მხარეს.

2. მონიშნეთ ნულების მდებარეობა რიცხვთა ღერძზე და დაადგინეთ მათი სიმრავლე (თუკ მე არის ლუწი, მაშინ ნული არის ლუწი სიმრავლე თუკ მე კენტი კენტია).

3. იპოვეთ ფუნქციის ნიშნები მის ნულებს შორის ინტერვალებში, დაწყებული ყველაზე მარჯვენა ინტერვალიდან: ამ ინტერვალში უტოლობის მარცხენა მხარეს ფუნქცია ყოველთვის დადებითია უტოლობების მოცემული ფორმისთვის. მარჯვნიდან მარცხნივ გადაადგილებისას ფუნქციის ნულზე ერთი ინტერვალიდან მიმდებარე ინტერვალზე უნდა გავითვალისწინოთ:

თუ ნული კენტია სიმრავლე, ფუნქციის ნიშანი იცვლება,

თუ ნული ლუწია სიმრავლე, შენარჩუნებულია ფუნქციის ნიშანი.

4. დაწერეთ პასუხი.

მაგალითი:

(x + 6) (x + 1) (X - 4) < 0.

ნაპოვნია ფუნქცია ნულები. ისინი თანაბარია:X 1 = -6; X 2 = -1; X 3 = 4.

კოორდინატთა წრფეზე ფუნქციის ნულები აღვნიშნოთვ ( x ) = (x + 6) (x + 1) (X - 4).

ვიპოვოთ ამ ფუნქციის ნიშნები თითოეულ ინტერვალში (-∞; -6), (-6; -1), (-1; 4) და

ნახატიდან ირკვევა, რომ უტოლობის ამონახსნების სიმრავლე არის (-∞; -6) და (-1; 4) ინტერვალების გაერთიანება.

პასუხი: (-∞ ; -6) და (-1; 4).

უტოლობების ამოხსნის განხილულ მეთოდს ე.წინტერვალის მეთოდი.

განსაზღვრების დომენი და ფუნქციის მნიშვნელობების დიაპაზონი. IN ელემენტარული მათემატიკაფუნქციები შესწავლილია მხოლოდ რეალური რიცხვების სიმრავლეზე რეს ნიშნავს, რომ ფუნქციის არგუმენტს შეუძლია მიიღოს მხოლოდ ის რეალური მნიშვნელობები, რომლებისთვისაც არის განსაზღვრული ფუნქცია, ე.ი. ის ასევე იღებს მხოლოდ რეალურ ღირებულებებს. Რამოდენიმე Xყველა მოქმედებს რეალური ღირებულებებიარგუმენტი x, რისთვისაც ფუნქცია წ= ვ(x) განისაზღვრა, მოუწოდა ფუნქციის დომენი. Რამოდენიმე იყველა რეალური ღირებულება წ, რომელსაც ფუნქცია იღებს, ეწოდება ფუნქციის დიაპაზონი. ახლა შეგიძლიათ მეტი მისცეთ ზუსტი განმარტებაᲛახასიათებლები: წესიX და Y სიმრავლეს შორის შესაბამისობის (კანონი)., რომლის მიხედვითაც სიმრავლიდან თითოეული ელემენტისთვისX-ს შეუძლია მოძებნოს ერთი და მხოლოდ ერთი ელემენტი Y სიმრავლიდან, რომელსაც ფუნქცია ეწოდება.

ამ განმარტებიდან გამომდინარეობს, რომ ფუნქცია განიხილება განსაზღვრულად, თუ:

მითითებულია ფუნქციის დომენი X ;

მითითებულია ფუნქციის დიაპაზონი ი ;

მიმოწერის წესი (კანონი) ცნობილია და ისეთი, რომ თითოეული

მხოლოდ ერთი ფუნქციის მნიშვნელობა შეიძლება მოიძებნოს არგუმენტის მნიშვნელობისთვის.

ფუნქციის გაურკვევლობის ეს მოთხოვნა სავალდებულოა.

მონოტონური ფუნქცია.თუ არგუმენტის რომელიმე ორი მნიშვნელობისთვის x 1 და x 2 მდგომარეობა x 2 > x 1 მოყვება ვ(x 2) > ვ(x 1), შემდეგ ფუნქცია ვ(x) ეწოდება იზრდება; თუ რომელიმესთვის x 1 და x 2 მდგომარეობა x 2 > x 1 მოყვება ვ(x 2) < ვ(x 1), შემდეგ ფუნქცია ვ(x) ეწოდება მცირდება. ფუნქციას, რომელიც მხოლოდ იზრდება ან მხოლოდ მცირდება, ეწოდება ერთფეროვანი.

შეზღუდული და შეუზღუდავი ფუნქციები.ფუნქციას ეძახიან შეზღუდული, თუ ასეთი რამ არსებობს დადებითი რიცხვი მრა | ვ(x) | მყველა ღირებულებისთვის x.თუ ასეთი რიცხვი არ არსებობს, მაშინ ფუნქცია არის შეუზღუდავი.

მაგალითები.

3-ზე ნაჩვენები ფუნქცია შეზღუდულია, მაგრამ არა მონოტონური. 4-ში მოცემული ფუნქცია არის საპირისპირო, მონოტონური, მაგრამ შეუზღუდავი. (განმარტეთ ეს გთხოვთ!).

უწყვეტი და უწყვეტი ფუნქციები.ფუნქცია წ = ვ (x) ეწოდება უწყვეტი წერტილშიx = ა, თუ:

1) ფუნქცია განისაზღვრება, როდესაც x = ა, ე.ი. ვ (ა) არსებობს;

2) არსებობს სასრულილიმიტის ლიმიტი ვ (x) ;

x→ა

(იხ. ფუნქციის ლიმიტები)

3) ვ (ა) = ლიმ ვ (x) .

x→ა

თუ ამ პირობებიდან ერთი მაინც არ არის დაკმაყოფილებული, მაშინ ფუნქცია გამოიძახება ასაფეთქებელიწერტილში x = ა.

თუ ფუნქცია უწყვეტია დროს ყველას მისი განმარტების სფეროს წერტილები, მაშინ ე.წ უწყვეტი ფუნქცია.

ლუწი და კენტი ფუნქციები.თუ ამისთვის ნებისმიერი x ვ(- x) = ვ (x), შემდეგ ფუნქცია გამოიძახება თუნდაც; თუ ეს მოხდება: ვ(- x) = - ვ (x), შემდეგ ფუნქცია გამოიძახება კენტი. ლუწი ფუნქციის გრაფიკი სიმეტრიული Y ღერძის მიმართ(სურ. 5), კენტი ფუნქციის გრაფიკი სიმმეტრიკა წარმოშობის მიმართ(ნახ. 6).

პერიოდული ფუნქცია.ფუნქცია ვ (x) - პერიოდული, თუ ასეთი რამ არსებობს არანულოვანინომერი თრისთვის ნებისმიერი xფუნქციის განსაზღვრის დომენიდან მოქმედებს შემდეგი: ვ (x + თ) = ვ (x). ეს სულ მცირენომერს ეძახიან ფუნქციის პერიოდი. ყველა ტრიგონომეტრიული ფუნქციებიპერიოდულია.

მაგალითი 1. დაამტკიცე ეს ცოდვა xაქვს 2 პერიოდი.

გამოსავალი: ჩვენ ვიცით, რომ ცოდვა ( x+ 2ნ) = ცოდვა x, სად ნ= 0, ± 1, ± 2, ...

ამიტომ, დამატება 2 ნარა სინუს არგუმენტამდე

ცვლის მის მნიშვნელობას. არის სხვა ნომერი ამით?

იგივე ქონება?

მოდი ვიჩვენოთ, რომ პ- ასეთი რიცხვი, ე.ი. თანასწორობა:

ცოდვა ( x+P) = ცოდვა x,

მოქმედებს ნებისმიერი ღირებულებისთვის x. მაგრამ შემდეგ აქვს

ადგილი და დრო x= / 2, ე.ი.

ცოდვა (/2 + პ) = ცოდვა / 2 = 1.

მაგრამ შემცირების ფორმულის მიხედვით sin (/2 + პ) = cos პ. მაშინ

ბოლო ორი ტოლობიდან გამომდინარეობს, რომ cos პ= 1, მაგრამ ჩვენ

ჩვენ ვიცით, რომ ეს მართალია მხოლოდ მაშინ პ = 2ნ. ვინაიდან ყველაზე პატარა

არანულოვანი რიცხვი 2-დან ნარის 2, მაშინ ეს რიცხვი

და არის პერიოდის ცოდვა x. ანალოგიურად შეიძლება დადასტურდეს, რომ 2საწყისი ნარის , ასე რომ, ეს არის ცოდვის 2 პერიოდი x.

ფუნქცია ნულები.არგუმენტის მნიშვნელობა, რომლის დროსაც ფუნქცია 0-ის ტოლია, გამოძახებულია ნული (root) ფუნქცია. ფუნქციას შეიძლება ჰქონდეს მრავალი ნული, მაგალითად, ფუნქცია წ = x (x + 1) (x-3) აქვს სამი ნული: x= 0, x= -1, x= 3. გეომეტრიულად null ფუნქცია - ეს არის ფუნქციის გრაფიკის ღერძთან გადაკვეთის წერტილის აბსცისა X .

ნახაზი 7 გვიჩვენებს ფუნქციის გრაფიკს ნულებით: x= ა, x = ბდა x= გ.

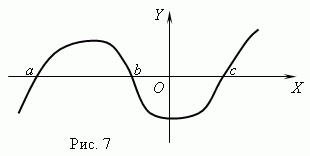
ასიმპტოტი.თუ ფუნქციის გრაფიკი განუსაზღვრელი ვადით უახლოვდება გარკვეულ ხაზს, რადგან ის საწყისს შორდება, მაშინ ამ წრფეს ე.წ. ასიმპტოტი.

განმარტება: რიცხვითი ფუნქცია არის კორესპონდენცია, რომელიც აკავშირებს თითოეულ x რიცხვს მოცემული სიმრავლიდან მხოლობითიწ.

Დანიშნულება:

სადაც x არის დამოუკიდებელი ცვლადი (არგუმენტი), y არის დამოკიდებული ცვლადი (ფუნქცია). x-ის მნიშვნელობების სიმრავლეს ეწოდება ფუნქციის დომენი (აღნიშნულია D(f)). y-ის მნიშვნელობების სიმრავლეს ეწოდება ფუნქციის მნიშვნელობების დიაპაზონი (აღნიშნულია E(f)). ფუნქციის გრაფიკი არის წერტილების სიმრავლე სიბრტყეში კოორდინატებით (x, f(x))

ფუნქციის მითითების მეთოდები.

1. ანალიტიკური მეთოდი (მათემატიკური ფორმულის გამოყენებით);
2. ცხრილის მეთოდი (ცხრილის გამოყენებით);
3. აღწერითი მეთოდი (სიტყვიერი აღწერის გამოყენებით);
4. გრაფიკული მეთოდი (გრაფიკის გამოყენებით).

ფუნქციის ძირითადი თვისებები.

1. ლუწი და კენტი

ფუნქცია იწოდება მაშინაც კი, თუ
– ფუნქციის განსაზღვრის დომენი სიმეტრიულია ნულის მიმართ
f(-x) = f(x)

ლუწი ფუნქციის გრაფიკი სიმეტრიულია ღერძის მიმართ 0 წ

ფუნქციას ეწოდება კენტი თუ
– ფუნქციის განსაზღვრის დომენი სიმეტრიულია ნულის მიმართ
– ნებისმიერი x-ისთვის განმარტების დომენიდან f(-x) = –f(x)

განრიგი უცნაური ფუნქციასიმეტრიული წარმოშობის მიმართ.

2. სიხშირე

ფუნქცია f(x) ეწოდება პერიოდულ პერიოდს, თუ რომელიმე x-ისთვის განსაზღვრების სფეროდან f(x) = f(x+T) = f(x-T) .

განრიგი პერიოდული ფუნქციაშედგება შეუზღუდავად განმეორებადი იდენტური ფრაგმენტებისგან.

3. ერთფეროვნება (მზარდი, კლებადი)

ფუნქცია f(x) იზრდება P სიმრავლეზე, თუ რომელიმე x 1 და x 2 ამ სიმრავლიდან ისე, რომ x 1

ფუნქცია f(x) მცირდება P სიმრავლეზე, თუ რომელიმე x 1 და x 2 ამ სიმრავლიდან, ისე, რომ x 1 f(x 2) .

4. უკიდურესობები

X max წერტილს უწოდებენ f(x) ფუნქციის მაქსიმალურ წერტილს, თუ X max-ის რომელიმე სამეზობლოდან ყველა x-ისთვის დაკმაყოფილებულია უტოლობა f(x) f(X max).

მნიშვნელობა Y max =f(X max) ეწოდება ამ ფუნქციის მაქსიმუმს.

X max – მაქსიმალური ქულა
მაქსიმუმ - მაქსიმუმ

X min წერტილი ეწოდება f(x) ფუნქციის მინიმალურ წერტილს, თუ X min-ის რომელიმე უბნის ყველა x-ისთვის დაკმაყოფილებულია უტოლობა f(x) f(X min).

მნიშვნელობა Y min =f(X min) ეწოდება ამ ფუნქციის მინიმუმს.

X წთ – მინიმალური ქულა
Y წთ – მინიმალური

X min , X max – ექსტრემალური წერტილები
Y min , Y max – ექსტრემა.

5. ფუნქციის ნულები

y = f(x) ფუნქციის ნული არის x არგუმენტის მნიშვნელობა, რომლის დროსაც ფუნქცია ხდება ნული: f(x) = 0.

X 1, X 2, X 3 – y = f(x) ფუნქციის ნულები.

ამოცანები და ტესტები თემაზე "ფუნქციის ძირითადი თვისებები"

• ფუნქციის თვისებები - რიცხვითი ფუნქციებიმე-9 კლასი

  გაკვეთილი: 2 დავალება: 11 ტესტი: 1

• ლოგარითმების თვისებები - ექსპონენციალური და ლოგარითმული ფუნქციების კლასი 11

  გაკვეთილი: 2 დავალება: 14 ტესტი: 1

• კვადრატული ფესვის ფუნქცია, მისი თვისებები და გრაფიკი - ფუნქცია კვადრატული ფესვი. კვადრატული ფესვის მე-8 კლასის თვისებები

  გაკვეთილები: 1 დავალება: 9 ტესტი: 1

• სიმძლავრის ფუნქციები, მათი თვისებები და გრაფიკები - გრადუსები და ფესვები. დენის ფუნქციები 11 კლასი

  გაკვეთილი: 4 დავალება: 14 ტესტი: 1

• ფუნქციები - მნიშვნელოვანი თემებიამისთვის ერთიანი სახელმწიფო გამოცდის განმეორებამათემატიკა

  ამოცანები: 24

ამ თემის შესწავლის შემდეგ თქვენ უნდა შეძლოთ განსაზღვრების დომენის პოვნა სხვადასხვა ფუნქციები, გრაფიკების გამოყენებით ფუნქციის ერთფეროვნების ინტერვალების დადგენა, ტოლობისა და უცნაურობის ფუნქციების შემოწმება. განვიხილოთ გამოსავალი მსგავსი ამოცანებიშემდეგი მაგალითების გამოყენებით.

მაგალითები.

1. იპოვეთ ფუნქციის განსაზღვრის დომენი.

გამოსავალი:ფუნქციის განსაზღვრის დომენი გვხვდება მდგომარეობიდან

ამ თემის გასაგებად განვიხილოთ გრაფიკზე გამოსახული ფუნქცია // ვაჩვენოთ, როგორ გაძლევს ფუნქციის გრაფიკი მისი თვისებების განსაზღვრის საშუალებას.

მოდით შევხედოთ ფუნქციის თვისებებს მაგალითის გამოყენებით

ფუნქციის განსაზღვრის დომენი არის span [3.5; 5.5].

ფუნქციის მნიშვნელობების დიაპაზონი არის span [1; 3].

1. x = -3, x = - 1, x = 1,5, x = 4,5 დროს, ფუნქციის მნიშვნელობა არის ნული.

არგუმენტის მნიშვნელობას, რომლის დროსაც ფუნქციის მნიშვნელობა არის ნული, ეწოდება ფუნქცია ნული.

//ისინი. ამ ფუნქციისთვის რიცხვებია -3;-1;1,5; 4.5 არის ნული.

2. ინტერვალებით [4.5; 3) და (1; 1.5) და (4.5; 5.5] f ფუნქციის გრაფიკი მდებარეობს აბსცისის ღერძის ზემოთ, ხოლო (-3; -1) და (1.5; 4.5) ინტერვალებში აბსცისის ღერძის ქვემოთ, ის. აიხსნება ასე - ინტერვალებით[4.5; 3) და (1; 1.5) და (4.5; 5.5] ფუნქცია იღებს დადებით მნიშვნელობებს, ხოლო ინტერვალებზე (-3; -1) და (1.5; 4.5) უარყოფით მნიშვნელობებს.

თითოეულ მითითებულ ინტერვალს (სადაც ფუნქცია იღებს იმავე ნიშნის მნიშვნელობებს) ეწოდება f.//ე.ი. ფუნქციის მუდმივი ნიშნის ინტერვალი. მაგალითად, თუ ავიღებთ ინტერვალს (0; 3), მაშინ ეს არ არის ამ ფუნქციის მუდმივი ნიშნის ინტერვალი.

მათემატიკაში, ფუნქციის მუდმივი ნიშნის ინტერვალების ძიებისას, ჩვეულებრივ მიეთითება მაქსიმალური სიგრძის ინტერვალები. //ამათ. ინტერვალი (2; 3) არის ნიშნის მუდმივობის ინტერვალიფუნქცია f, მაგრამ პასუხი უნდა მოიცავდეს ინტერვალს [4.5; 3) რომელიც შეიცავს ინტერვალს (2; 3).

3. თუ გადაადგილდებით x ღერძის გასწვრივ 4.5-დან 2-მდე, შეამჩნევთ, რომ ფუნქციის გრაფიკი ქვევით მიდის, ანუ ფუნქციის მნიშვნელობები მცირდება. //მათემატიკაში მიღებულია იმის თქმა, რომ ინტერვალზე [4.5; 2] ფუნქცია მცირდება.

x იზრდება 2-დან 0-მდე, ფუნქციის გრაფიკი მაღლა იწევს, ე.ი. ფუნქციის მნიშვნელობები იზრდება. //მათემატიკაში მიღებულია იმის თქმა, რომ ინტერვალზე [ 2; 0] ფუნქცია იზრდება.

ფუნქცია f იწოდება, თუ არგუმენტის x1 და x2 ნებისმიერი ორი მნიშვნელობისთვის ამ ინტერვალიდან ისეთი, რომ x2 > x1, მოქმედებს უტოლობა f (x2) > f (x1). // ან ფუნქციას ეძახიან იზრდება გარკვეული ინტერვალით, თუ ამ ინტერვალიდან არგუმენტის რომელიმე მნიშვნელობისთვის, არგუმენტის უფრო დიდი მნიშვნელობა შეესაბამება ფუნქციის უფრო დიდ მნიშვნელობას.//ე.ი. რაც მეტი x, მეტი y.

ფუნქცია f ეწოდება მცირდება გარკვეული ინტერვალით, თუ არგუმენტის ნებისმიერი ორი მნიშვნელობისთვის x1 და x2 ამ ინტერვალიდან ისეთი, რომ x2 > x1, უტოლობა f(x2) მცირდება რაღაც ინტერვალზე, თუ არგუმენტის რომელიმე მნიშვნელობისთვის ამ ინტერვალიდან უფრო დიდი მნიშვნელობა არგუმენტი შეესაბამება ფუნქციის უფრო მცირე მნიშვნელობას. //ისინი. რაც მეტი x მით ნაკლებია y.

თუ ფუნქცია იზრდება განსაზღვრების მთელ დომენზე, მაშინ მას უწოდებენ იზრდება.

თუ ფუნქცია მცირდება განსაზღვრების მთელ დომენზე, მაშინ მას უწოდებენ მცირდება.

მაგალითი 1.მზარდი და კლებადი ფუნქციების გრაფიკი, შესაბამისად.

მაგალითი 2.

განსაზღვრეთ ფენომენი. წრფივი ფუნქცია f(x) = 3x + 5 იზრდება თუ კლებადი?

მტკიცებულება. მოდით გამოვიყენოთ განმარტებები. მოდით x1 და x2 იყოს არგუმენტის თვითნებური მნიშვნელობები და x1< x2., например х1=1, х2=7

საზღვრები და უწყვეტობა

კომპლექტი

ქვეშ ბევრიგაგებულია, როგორც ერთგვაროვანი ობიექტების ერთობლიობა. ობიექტებს, რომლებიც ქმნიან კომპლექტს, ეწოდება ელემენტებიან წერტილებიამ სიმრავლის. კომპლექტები აღნიშნავენ დიდი ასოებითდა მათი ელემენტები მცირეა. თუ ანაკრების ელემენტია ა, მაშინ ჩანაწერი გამოიყენება აÎ ა. თუ ბარ არის ნაკრების ელემენტი ა, შემდეგ ასე წერია: ბ Ï ა. სიმრავლეს, რომელიც არ შეიცავს ერთ ელემენტს, ეწოდება ცარიელი სიმრავლე და აღინიშნება შემდეგნაირად: Ø.

თუ კომპლექტი ბშედგება ნაკრების ელემენტების ნაწილისგან აან ემთხვევა მას, მაშინ კომპლექტი ბდაურეკა ქვეჯგუფიადგენს და აღნიშნავს ბÌ ა.

ორი კომპლექტი ე.წ თანაბარი, თუ ისინი შედგება ერთი და იგივე ელემენტებისაგან.

ასოციაციაორი კომპლექტი ადა ბკომპლექტს უწოდებენ C, რომელიც შედგება ყველა ელემენტისგან, რომელიც მიეკუთვნება მინიმუმ ერთ კომპლექტს: C=აÈ ბ.

გადაკვეთითორი კომპლექტი ადა ბკომპლექტს უწოდებენ C, რომელიც შედგება ყველა ელემენტისგან, რომელიც ეკუთვნის თითოეულ ამ კომპლექტს: C=აÇ ბ.

განსხვავებითკომპლექტი ადა ბკომპლექტს უწოდებენ ე ა, რომლებიც არ მიეკუთვნება კომპლექტს ბ: .

დანამატიკომპლექტი აÌ ბკომპლექტს უწოდებენ C, რომელიც შედგება ნაკრების ყველა ელემენტისგან ბ, არ ეკუთვნის ა.

კომპლექტები, რომელთა ელემენტებია რეალური რიცხვები, უწოდებენ რიცხვითი:

სადაც ნÌ ზÌ ქÌ რ, მეÌ რდა რ=მეÈ ქ.

Რამოდენიმე X, რომლის ელემენტები აკმაყოფილებენ უტოლობას ეწოდება სეგმენტი(სეგმენტი) და აღინიშნება [ ა; ბ]; უთანასწორობა ა<x<ბ – ინტერვალიდა აღინიშნება ()-ით; უტოლობები და - ნახევარი ინტერვალებითდა აღინიშნება და შესაბამისად. ასევე ხშირად გიწევს საქმე უსასრულო ინტერვალებთან და ნახევარინტერვალებთან: , , , და . მოსახერხებელია ყველას დარეკვა ინტერვალებით .

ინტერვალი, ე.ი. უტოლობის დამაკმაყოფილებელი პუნქტების ნაკრები (სად), წერტილის სამეზობლო ეწოდება ა.

ფუნქციის კონცეფცია. ფუნქციის ძირითადი თვისებები

თუ თითოეული ელემენტი xკომპლექტი Xერთი ელემენტი ემთხვევა წკომპლექტი ი, მერე ამას გადასაღებ მოედანზე ამბობენ Xმოცემული ფუნქცია წ=ვ(x). სადაც xდაურეკა დამოუკიდებელი ცვლადიან არგუმენტი, ა წ – დამოკიდებული ცვლადიან ფუნქცია, ა ვაღნიშნავს შესაბამისობის კანონს. Რამოდენიმე Xდაურეკა განმარტების სფეროფუნქციები და ნაკრები ი – ღირებულებების დიაპაზონიფუნქციები.

ფუნქციების დაზუსტების რამდენიმე გზა არსებობს.

1) ანალიტიკური მეთოდი - ფუნქცია მოცემულია ფორმის ფორმულით წ=ვ(x).

2) ტაბულური მეთოდი - ფუნქცია მითითებულია ცხრილით, რომელიც შეიცავს არგუმენტების მნიშვნელობებს და შესაბამისი ფუნქციის მნიშვნელობებს წ=ვ(x).

3) გრაფიკული მეთოდი - ფუნქციის გრაფიკის გამოსახვა, ე.ი. ქულების ნაკრები ( x; წ) საკოორდინაციო თვითმფრინავი, რომელთა აბსციები წარმოადგენს არგუმენტის მნიშვნელობებს, ხოლო ორდინატები წარმოადგენს შესაბამის ფუნქციის მნიშვნელობებს წ=ვ(x).

4) ვერბალური მეთოდი - ფუნქცია აღწერილია მისი შემადგენლობის წესით. მაგალითად, დირიხლეს ფუნქცია იღებს მნიშვნელობას 1 if xრაციონალური რიცხვია და 0 თუ x- ირაციონალური რიცხვი.

გამოირჩევა ფუნქციების შემდეგი ძირითადი თვისებები.

1 ლუწი და კენტიფუნქცია წ=ვ(x) ეწოდება თუნდაც, თუ რაიმე მნიშვნელობისთვის xმისი განმარტების სფეროდან დაკმაყოფილებულია ვ(–x)=ვ(x), და კენტი, თუ ვ(–x)=–ვ(x). თუ არცერთი ზემოთ ჩამოთვლილი თანასწორობა არ არის დაკმაყოფილებული, მაშინ წ=ვ(x) ეწოდება ზოგადი ფუნქცია. ლუწი ფუნქციის გრაფიკი სიმეტრიულია ღერძის მიმართ ოიდა კენტი ფუნქციის გრაფიკი სიმეტრიულია წარმოშობის მიმართ.

2 ერთფეროვნებაფუნქცია წ=ვ(x) ეწოდება იზრდება (მცირდება) ინტერვალზე X, თუ ამ ინტერვალიდან უფრო დიდი არგუმენტის მნიშვნელობა შეესაბამება უფრო დიდ (პატარა) ფუნქციის მნიშვნელობას. დაე x 1 ,x 2 Î X, x 2 >x 1 . შემდეგ ფუნქცია იზრდება ინტერვალზე X, თუ ვ(x 2)>ვ(x 1) და მცირდება, თუ ვ(x 2)<ვ(x 1).

მზარდი და კლებადი ფუნქციების პარალელურად განიხილება არაკლებადი და არამზარდი ფუნქციები. ფუნქციას ეძახიან არ კლებულობს (არ მზარდი), თუ ზე x 1 ,x 2 Î X, x 2 >xმოქმედებს 1 უტოლობა ვ(x 2)≥ვ(x 1) (ვ(x 2)≤ვ(x 1)).

მზარდი და კლებადი ფუნქციები, ისევე როგორც არამზარდი და შეუმცირებელი ფუნქციები მონოტონურია.

3 შეზღუდულიფუნქცია წ=ვ(x) ინტერვალზე შეზღუდული ეწოდება X, თუ არის ასეთი დადებითი რიცხვი მ>0, რა | ვ(x)|≤მვინმესთვის xÎ X. IN წინააღმდეგ შემთხვევაშინათქვამია, რომ ფუნქცია შეუზღუდავია X.

4 სიხშირეფუნქცია წ=ვ(x) ეწოდება პერიოდულ პერიოდს თ≠0, თუ რომელიმე xფუნქციის დომენიდან ვ(x+თ)=ვ(x). შემდეგში, პერიოდში ვგულისხმობთ ფუნქციის უმცირეს პოზიტიურ პერიოდს.

ფუნქციას ეძახიან გამოკვეთილითუ იგი მოცემულია ფორმის ფორმულით წ=ვ(x). თუ ფუნქცია მოცემულია განტოლებით ფ(x, წ)=0, დაუშვებელია დამოკიდებული ცვლადის მიმართ წ, მაშინ ე.წ იმპლიციტური.

დაე წ=ვ(x) არის კომპლექტზე განსაზღვრული დამოუკიდებელი ცვლადის ფუნქცია Xდიაპაზონით ი. მოდით დავამთხვიოთ თითოეული წÎ იერთი მნიშვნელობა xÎ X, რომელიც ვ(x)=წ.მაშინ მიღებული ფუნქცია x=φ (წ), განსაზღვრულია კომპლექტში იდიაპაზონით X, დაურეკა საპირისპიროდა დანიშნულია წ=ვ –1 (x). გრაფიკები ორმხრივად შებრუნებული ფუნქციებისიმეტრიული შედარებით პირველი და მესამე კოორდინატთა მეოთხედის ბისექტორთან.

დაუშვით ფუნქცია წ=ვ(u) არის ცვლადის ფუნქცია u, განსაზღვრული კომპლექტში უდიაპაზონით იდა ცვლადი uთავის მხრივ არის ფუნქცია u=φ (x), განსაზღვრულია ნაკრებზე Xდიაპაზონით უ. შემდეგ გადაცემულია Xფუნქცია წ=ვ(φ (x)) ეწოდება რთული ფუნქცია (ფუნქციების შედგენა, ფუნქციების სუპერპოზიცია, ფუნქციის ფუნქცია).

ელემენტარული ფუნქციები

ძირითადი ელემენტარული ფუნქციები მოიცავს:

• დენის ფუნქცია წ=x n; წ=x–nდა წ=x 1/ ნ;
• ექსპონენციალური ფუნქცია წ=ნაჯახი;
• ლოგარითმული ფუნქცია წ= ჟურნალი ნაჯახი;
• ტრიგონომეტრიული ფუნქციები წ=ცოდვა x, წ= cos x, წ= tg xდა წ=ctg x;
• შებრუნებული ტრიგონომეტრიული ფუნქციები წ= რკალი x, წ=არქოსი x, წ=arctg xდა წ=arcctg x.

მთავარი ელემენტარული ფუნქციებიახალი ფუნქციების მიღება შესაძლებელია გამოყენებით ალგებრული ოპერაციებიდა ფუნქციების სუპერპოზიცია.

ძირითადი ელემენტარული ფუნქციებიდან აგებულ ფუნქციებს ალგებრული მოქმედებების სასრული რაოდენობის და სუპერპოზიციის ოპერაციების სასრული რაოდენობის გამოყენებით ე.წ. ელემენტარული.

ალგებრულიეწოდება ფუნქცია, რომელშიც არგუმენტი ხორციელდება საბოლოო ნომერიალგებრული ოპერაციები. ალგებრული ფუნქციები მოიცავს:

· მთლიანი რაციონალური ფუნქცია(პოლინომი ან მრავალწევრი)

· წილადი რაციონალური ფუნქცია(ორი მრავალწევრის თანაფარდობა)

· ირაციონალური ფუნქცია(თუ არგუმენტზე ოპერაციები მოიცავს ფესვის ამოღებას).

ნებისმიერ არაალგებრულ ფუნქციას ეწოდება ტრანსცენდენტული. ტრანსცენდენტურ ფუნქციებში შედის ექსპონენციალური, ლოგარითმული, ტრიგონომეტრიული და შებრუნებული ტრიგონომეტრიული ფუნქციები.