ბურთის განმარტება. მათემატიკა

ბურთი არის სხეული, რომელიც შედგება სივრცის ყველა წერტილისგან, რომლებიც მდებარეობს მოცემული წერტილიდან მოცემულზე არაუმეტეს მანძილზე. ამ წერტილს ბურთის ცენტრი ეწოდება, ხოლო ამ მანძილს ბურთის რადიუსი. ბურთის საზღვარს სფერულ ზედაპირს ან სფეროს უწოდებენ. სფეროს წერტილები არის ბურთის ყველა წერტილი, რომელიც ამოღებულია ცენტრიდან რადიუსის ტოლ მანძილზე. ნებისმიერ სეგმენტს, რომელიც აკავშირებს ბურთის ცენტრს სფერული ზედაპირის წერტილთან, ასევე ეწოდება რადიუსი. სეგმენტს, რომელიც გადის ბურთის ცენტრში და აკავშირებს სფერულ ზედაპირზე ორ წერტილს, ეწოდება დიამეტრი. ნებისმიერი დიამეტრის ბოლოებს ბურთის დიამეტრულად საპირისპირო წერტილებს უწოდებენ.

ბურთი არის რევოლუციის სხეული, ისევე როგორც კონუსი და ცილინდრი. ბურთი მიიღება მისი დიამეტრის გარშემო ნახევარწრიული ღერძის სახით ბრუნვით.

ბურთის ზედაპირის ფართობი შეგიძლიათ იხილოთ ფორმულების გამოყენებით:

სადაც r არის ბურთის რადიუსი, d არის ბურთის დიამეტრი.

ბურთის მოცულობა გამოითვლება ფორმულით:

V = 4 / 3 πr 3,

სადაც r არის ბურთის რადიუსი.

თეორემა. სიბრტყით ბურთის ყოველი მონაკვეთი არის წრე. ამ წრის ცენტრი არის ბურთის ცენტრიდან საჭრელ სიბრტყეზე გამოყვანილი პერპენდიკულარულის საფუძველი.

ამ თეორემიდან გამომდინარე, თუ ბურთი O ცენტრით და R რადიუსით იკვეთება α სიბრტყით, მაშინ განივი კვეთის შედეგად მიიღება r რადიუსის წრე K ცენტრით. სიბრტყით ბურთის მონაკვეთის რადიუსი შეიძლება იყოს. ნაპოვნია ფორმულით

ფორმულიდან ირკვევა, რომ ცენტრიდან თანაბარი სიბრტყეები კვეთენ ბურთს თანაბარ წრეებში. მონაკვეთის რადიუსი უფრო დიდია, რაც უფრო ახლოს არის ჭრის თვითმფრინავი ბურთის ცენტრთან, ანუ მით უფრო მცირეა მანძილი OK. ყველაზე დიდ რადიუსს აქვს სიბრტყის მონაკვეთი, რომელიც გადის ბურთის ცენტრში. ამ წრის რადიუსი უდრის ბურთის რადიუსს.

ბურთის ცენტრში გამავალ თვითმფრინავს ცენტრალური სიბრტყე ეწოდება. ბურთის მონაკვეთს დიამეტრული სიბრტყით ეწოდება დიდი წრე, ხოლო სფეროს მონაკვეთს - დიდი წრე, ხოლო სფეროს მონაკვეთს - დიდი წრე.

თეორემა. ბურთის ნებისმიერი დიამეტრული სიბრტყე არის მისი სიმეტრიის სიბრტყე. ბურთის ცენტრი მისი სიმეტრიის ცენტრია.

სიბრტყეს, რომელიც გადის სფერული ზედაპირის A წერტილში და პერპენდიკულარულია A წერტილამდე მიყვანილი რადიუსზე, ტანგენტური სიბრტყე ეწოდება. A წერტილს ტანგენტს უწოდებენ.

თეორემა. ტანგენტის სიბრტყეს აქვს მხოლოდ ერთი საერთო წერტილი ბურთთან - შეხების წერტილი.

სწორ ხაზს, რომელიც გადის სფერული ზედაპირის A წერტილში ამ წერტილამდე მიყვანილი რადიუსის პერპენდიკულარულად, ტანგენსი ეწოდება.

თეორემა. ტანგენტების უსასრულო რაოდენობა გადის სფერული ზედაპირის ნებისმიერ წერტილში და ყველა მათგანი დევს ბურთის ტანგენტურ სიბრტყეში.

სფერული სეგმენტი არის ბურთის ნაწილი, რომელიც მოწყვეტილია მისგან თვითმფრინავით. წრე ABC არის სფერული სეგმენტის საფუძველი. ABC წრის N ცენტრიდან სფერულ ზედაპირთან კვეთამდე გამოყვანილი MN პერპენდიკულარული სეგმენტი არის სფერული სეგმენტის სიმაღლე. წერტილი M არის სფერული სეგმენტის წვერო.

სფერული სეგმენტის ზედაპირის ფართობი შეიძლება გამოითვალოს ფორმულის გამოყენებით:

სფერული სეგმენტის მოცულობა შეგიძლიათ იხილოთ ფორმულის გამოყენებით:

V = πh 2 (R – 1/3h),

სადაც R არის დიდი წრის რადიუსი, h არის სფერული სეგმენტის სიმაღლე.

სფერული სექტორი მიიღება სფერული სეგმენტიდან და კონუსიდან შემდეგნაირად. თუ სფერული სეგმენტი უფრო მცირეა ვიდრე ნახევარსფერო, მაშინ სფერულ სეგმენტს ავსებს კონუსი, რომლის წვერო ბურთის ცენტრშია, ხოლო ფუძე არის სეგმენტის საფუძველი. თუ სეგმენტი უფრო დიდია ვიდრე ნახევარსფერო, მაშინ მითითებული კონუსი ამოღებულია მისგან.

სფერული სექტორი არის ბურთის ნაწილი, რომელიც შემოსაზღვრულია სფერული სეგმენტის მრუდი ზედაპირით (ჩვენს ფიგურაში ეს არის AMCB) და კონუსური ზედაპირით (ჩვენს ფიგურაში ეს არის OABC), რომლის ფუძე არის ფუძე. სეგმენტი (ABC), ხოლო წვერო არის ბურთის ცენტრი O.

სფერული სექტორის მოცულობა გამოიხატება ფორმულით:

V = 2/3 πR 2 H.

სფერული ფენა არის ბურთის ნაწილი, რომელიც ჩაკეტილია ორ პარალელურ სიბრტყეს შორის (სიბრტყეები ABC და DEF ფიგურაში), რომლებიც კვეთენ სფერულ ზედაპირს. სფერული ფენის მრუდე ზედაპირს სფერული სარტყელი (ზონა) ეწოდება. წრეები ABC და DEF არის სფერული სარტყლის საფუძველი. მანძილი NK სფერული სარტყლის ფუძეებს შორის არის მისი სიმაღლე.

ვებსაიტზე, მასალის სრულად ან ნაწილობრივ კოპირებისას საჭიროა წყაროს ბმული.

ბურთი და სფერო, პირველ რიგში, გეომეტრიული ფიგურებია და თუ ბურთი გეომეტრიული სხეულია, მაშინ სფერო არის ბურთის ზედაპირი. ეს ციფრები საინტერესო იყო ჩვენს წელთაღრიცხვამდე მრავალი ათასი წლის წინ.

შემდგომში, როდესაც გაირკვა, რომ დედამიწა არის ბურთი და ცა არის ციური სფერო, შეიქმნა ახალი მომხიბლავი მიმართულება გეომეტრიაში - გეომეტრია სფეროზე ან სფერული გეომეტრია. იმისათვის, რომ ვისაუბროთ ბურთის ზომაზე და მოცულობაზე, ჯერ ის უნდა განისაზღვროს.

ბურთი

R რადიუსის ბურთი, რომელსაც აქვს ცენტრი O წერტილში გეომეტრიაში არის სხეული, რომელიც იქმნება სივრცის ყველა წერტილით, რომლებსაც აქვთ საერთო თვისება. ეს წერტილები განლაგებულია მანძილით, რომელიც არ აღემატება ბურთის რადიუსს, ანუ ისინი ავსებენ მთელ სივრცეს ბურთის რადიუსზე ნაკლებს მისი ცენტრიდან ყველა მიმართულებით. თუ გავითვალისწინებთ მხოლოდ იმ წერტილებს, რომლებიც თანაბარი მანძილით არიან დაშორებული ბურთის ცენტრიდან, განვიხილავთ მის ზედაპირს ან ბურთის გარსს.

როგორ მივიღო ბურთი? შეგვიძლია ქაღალდიდან გამოვჭრათ წრე და დავიწყოთ მისი შემობრუნება საკუთარი დიამეტრის გარშემო. ანუ წრის დიამეტრი იქნება ბრუნვის ღერძი. ჩამოყალიბებული ფიგურა იქნება ბურთი. ამიტომ, ბურთს ასევე უწოდებენ რევოლუციის სხეულს. რადგან ის შეიძლება ჩამოყალიბდეს ბრტყელი ფიგურის – წრის ბრუნვით.

ავიღოთ თვითმფრინავი და ამით დავჭრათ ჩვენი ბურთი. ისევე, როგორც დანით დავჭრათ ფორთოხალი. ნაწილს, რომელიც ჩვენ ვწყვეტთ ბურთს, ეწოდება სფერული სეგმენტი.

ძველ საბერძნეთში მათ იცოდნენ, თუ როგორ ემუშავათ არა მხოლოდ ბურთთან და სფეროსთან, როგორც გეომეტრიული ფიგურები, მაგალითად, მათი გამოყენება მშენებლობაში, არამედ იცოდნენ როგორ გამოეთვალათ ბურთის ზედაპირის ფართობი და ბურთის მოცულობა.

სფერო არის ბურთის ზედაპირის სხვა სახელი. სფერო არ არის სხეული - ეს არის რევოლუციის სხეულის ზედაპირი. თუმცა, რადგან დედამიწასაც და ბევრ სხეულსაც აქვს სფერული ფორმა, მაგალითად, წყლის წვეთი, ფართოდ გავრცელდა გეომეტრიული ურთიერთობების შესწავლა სფეროს შიგნით.

მაგალითად, თუ სფეროს ორ წერტილს დავუკავშირებთ ერთმანეთს სწორი ხაზით, მაშინ ამ სწორ ხაზს ეძახიან აკორდი და თუ ეს აკორდი გადის სფეროს ცენტრში, რომელიც ემთხვევა ბურთის ცენტრს, მაშინ აკორდი დაერქმევა სფეროს დიამეტრს.

თუ დავხაზავთ სწორ ხაზს, რომელიც ეხება სფეროს მხოლოდ ერთ წერტილში, მაშინ ამ წრფეს ტანგენსი ეწოდება. გარდა ამისა, სფეროს ეს ტანგენსი ამ წერტილში პერპენდიკულარული იქნება შეხების წერტილამდე მიყვანილი სფეროს რადიუსზე.

თუ აკორდს სფეროდან ერთი მიმართულებით ან მეორე მიმართულებით გავაგრძელებთ სწორ ხაზს, მაშინ ამ აკორდს სეკანტი დაერქმევა. ან შეიძლება სხვანაირად ვთქვათ - სფეროს სეკანტი თავის აკორდს შეიცავს.

ბურთის მოცულობა

ბურთის მოცულობის გამოთვლის ფორმულა არის:

სადაც R არის ბურთის რადიუსი.

თუ თქვენ გჭირდებათ სფერული სეგმენტის მოცულობის პოვნა, გამოიყენეთ ფორმულა:

V seg =πh 2 (R-h/3), h არის სფერული სეგმენტის სიმაღლე.

ბურთის ან სფეროს ზედაპირის ფართობი

სფეროს ან ბურთის ზედაპირის ფართობის გამოსათვლელად (ისინი იგივეა):

სადაც R არის სფეროს რადიუსი.

არქიმედეს ძალიან უყვარდა ბურთი და სფერო, მან სთხოვა კიდეც დაეტოვებინა ნახატი მის საფლავზე, რომელშიც ბურთი იყო ჩაწერილი ცილინდრში. არქიმედეს სჯეროდა, რომ ბურთისა და მისი ზედაპირის მოცულობა ტოლია ცილინდრის მოცულობის და ზედაპირის ორი მესამედისა, რომელშიც ბურთია ჩაწერილი“.

ბურთი (სფერო)

სფერული ზედაპირი. ბურთი (სფერო). ბურთის სექციები: წრეები.

არქიმედეს თეორემა. ბურთის ნაწილები: სფერული სეგმენტი,

სფერული ფენა, სფერული სარტყელი, სფერული სექტორი.

სფერული ზედაპირი - ეს წერტილების ლოკუსი(იმათ. ბევრიყველა ქულის რაოდენობა)სივრცეში, ერთი წერტილიდან თანაბარ მანძილზე ო , რომელსაც სფერული ზედაპირის ცენტრს უწოდებენ (სურ.90). რადიუსი AOi დიამეტრი AB განისაზღვრება ისევე, როგორც წრეში.

ბურთი (სფერო) - ეს სფერული ზედაპირით შემოსაზღვრული სხეული.შეუძლია მიიღეთ ბურთი ნახევარწრიულის როტაციით (ან წრე ) დიამეტრის გარშემო. ბურთის ყველა თვითმფრინავი არის წრეები (სურ.90 ). ყველაზე დიდი წრე დევს განყოფილებაში, რომელიც გადის ბურთის ცენტრში და ე.წ დიდი წრე. მისი რადიუსი უდრის ბურთის რადიუსს. ნებისმიერი ორი დიდი წრე იკვეთება ბურთის დიამეტრის გასწვრივ ( AB, სურ.91 ).ეს დიამეტრი ასევე არის დიდი წრეების გადაკვეთის დიამეტრი. სფერული ზედაპირის ორი წერტილის გავლით, რომელიც მდებარეობს იმავე დიამეტრის ბოლოებზე(A და B, სურ.91 ), შეგიძლიათ დახაზოთ უამრავი დიდი წრე. მაგალითად, უსასრულო რაოდენობის მერიდიანების დახატვა შესაძლებელია დედამიწის პოლუსებში.

სფეროს მოცულობა ერთნახევარჯერ ნაკლებია მის გარშემო შემოხაზული ცილინდრის მოცულობაზე. (სურ.92 ), ა ბურთის ზედაპირი ერთი და ნახევარი ჯერ ნაკლებია იმავე ცილინდრის მთლიან ზედაპირზე ( არქიმედეს თეორემა):

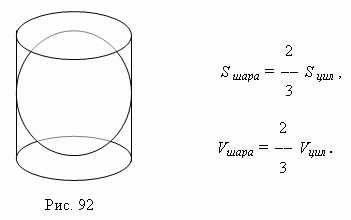
Აქ ს ბურთი და ვ ბურთი - ბურთის ზედაპირი და მოცულობა, შესაბამისად;

ს ცილი და ვ ცილი - შემოხაზული ცილინდრის მთლიანი ზედაპირი და მოცულობა.

ბურთის ნაწილები. ბურთის ნაწილი (სფერო) ), მოწყვიტა მას რაიმე თვითმფრინავით ( ABC, სურ.93), დაურეკა ბურთი(სფერული ) სეგმენტი. წრე ABC დაურეკა საფუძველიბურთის სეგმენტი. ხაზის სეგმენტი MN ცენტრიდან გამოყვანილი პერპენდიკულარული N წრე ABC სანამ ის არ იკვეთება სფერულ ზედაპირთან, ე.წ სიმაღლებურთის სეგმენტი. Წერტილიმ დაურეკა ზედაბურთის სეგმენტი.

სფეროს ნაწილი, რომელიც ჩაკეტილია ორ პარალელურ სიბრტყეს შორის ABC და DEF, რომლებიც კვეთენ სფერულ ზედაპირს (ნახ. 93), დაურეკა სფერული ფენა; სფერული ფენის მრუდი ზედაპირი ეწოდება ბურთის ქამარი(ზონა). წრეები ABC და DEF – საფუძველიბურთის ქამარი. მანძილინ.კ. სფერული სარტყლის ფუძეებს შორის - მისი სიმაღლე. ბურთის ნაწილი, რომელიც შემოსაზღვრულია სფერული სეგმენტის მრუდი ზედაპირით ( AMCB, სურ.93) და კონუსური ზედაპირი OABC , რომლის საფუძველია სეგმენტის საფუძველი ( ABC ), ხოლო წვერო არის ბურთის ცენტრიო , დაურეკა სფერული სექტორი.

როდესაც ადამიანებს ეკითხებიან განსხვავებას სფეროსა და ბურთს შორის, ბევრი უბრალოდ იჩეჩავს მხრებს, ფიქრობენ, რომ სინამდვილეში ისინი ერთი და იგივეა (წრისა და წრის ანალოგია). მართლაც, ყველა ჩვენგანმა კარგად ვიცით გეომეტრია სასკოლო სასწავლო გეგმიდან და შეუძლია ამ კითხვაზე დაუყოვნებლივ პასუხის გაცემა? სფეროს აქვს გარკვეული განსხვავებები ბურთისგან, რომელიც არა მხოლოდ სკოლის მოსწავლეებმა უნდა იცოდნენ, რომ კარგი შეფასება მიიღონ დემონსტრირებული ცოდნისთვის, არამედ მრავალი სხვა ადამიანიც, მაგალითად, რომელთა ნამუშევარი პირდაპირ კავშირშია ნახატებთან.

განმარტება

ბურთი- სივრცეში ყველა წერტილის ნაკრები. ყველა ეს წერტილი განლაგებულია გეომეტრიული სხეულის ცენტრიდან არაუმეტეს მოცემული მანძილით. ამ მანძილს თავად რადიუსი ეწოდება. ბურთი, როგორც გეომეტრიული სხეული, იქმნება შემდეგნაირად: ნახევარწრე ბრუნავს მის დიამეტრთან ახლოს. რაც შეეხება სფეროს, ეს არის ბურთის ზედაპირი (მაგალითად, დახურული ბურთი მოიცავს მას, ღია - არა). ბურთის ფართობის ან მოცულობის გამოთვლა მოიცავს მთელ გეომეტრიულ ფორმულებს, რომლებიც ძალიან რთულია, მიუხედავად თავად გეომეტრიული ფიგურის აშკარა სიმარტივისა.

სფეროროგორც ზემოთ აღინიშნა, არის ბურთის ზედაპირი, მისი გარსი. სივრცეში ყველა წერტილი თანაბარი მანძილითაა დაშორებული სფეროს ცენტრიდან. რაც შეეხება გეომეტრიული სხეულის რადიუსს, მას უწოდებენ ნებისმიერ სეგმენტს, რომლის ერთი წერტილი უშუალოდ სფეროს ცენტრია, ხოლო მეორე შეიძლება განთავსდეს ზედაპირის ნებისმიერ წერტილში. შეიძლება ითქვას, რომ სფერო არის ბურთის გარსი ყოველგვარი შინაარსის გარეშე (უფრო კონკრეტული მაგალითები მოცემულია ქვემოთ). ბურთის მსგავსად, სფერო არის ბრუნვის სხეული. სხვათა შორის, ბევრს ასევე აინტერესებს რა განსხვავებაა წრესა და წრეს შორის სფეროდან და ბურთიდან. აქ ყველაფერი მარტივია: პირველ შემთხვევაში ეს არის ფიგურები თვითმფრინავზე, მეორეში - სივრცეში.

შედარება

უკვე ითქვა, რომ სფერო არის ბურთის ზედაპირი, რაც უკვე იძლევა განსხვავების ერთ მნიშვნელოვან ნიშანზე საუბარი. განსხვავება ორ გეომეტრიულ სხეულს შორის შეინიშნება სხვა ასპექტებში:

• ბურთის ყველა წერტილი მდებარეობს ცენტრიდან ერთსა და იმავე მანძილზე, ხოლო სხეული შეზღუდულია ზედაპირით (სფერო, რომელიც შიგნით ცარიელია). სხვა სიტყვებით რომ ვთქვათ, სფერო ღრუა. როგორც წესი, გასაგებად მარტივი მაგალითია მოყვანილი ბუშტით და ბილიარდის ბურთით. ორივე ამ ობიექტს ბურთულებს უწოდებენ, მაგრამ პირველ შემთხვევაში საქმე გვაქვს სფეროსთან, მეორეში კი სრულფასოვან ბურთთან თავისი შიგთავსით.
• სფეროს აქვს თავისი ფართობი, მაგრამ მას არ აქვს მოცულობა. სფერო საპირისპიროა: მისი მოცულობა შეიძლება გამოითვალოს, ხოლო ფართობი არ აქვს. ზოგიერთმა შეიძლება თქვას, რომ ეს არის განსხვავების მთავარი ნიშანი, მაგრამ ის მხოლოდ მაშინ ჩნდება, თუ საჭიროა გარკვეული გამოთვლების გაკეთება (რთული გეომეტრიული ფორმულები). მაშასადამე, მთავარი განსხვავება ისაა, რომ სფერო ღრუა, ხოლო ბურთი არის სხეული შიგნით შიგთავსით.
• კიდევ ერთი განსხვავება მდგომარეობს რადიუსში. მაგალითად, სფეროს რადიუსი არ არის მხოლოდ წერტილების მანძილი ცენტრამდე. რადიუსი შეიძლება იყოს ნებისმიერი სეგმენტი, რომელიც აკავშირებს სფეროს წერტილს მის ცენტრთან. ყველა ეს სეგმენტი ერთმანეთის ტოლია. რაც შეეხება ბურთს, მის შიგნით მდებარე წერტილები ცენტრიდან რადიუსზე ნაკლებია დაშორებული (ზუსტად მის შემოსაზღვრული სფეროს გამო).

დასკვნების საიტი

1. სფერო ღრუა, ხოლო ბურთი შიგნით სავსე სხეულია. მაგალითად, ჰაერის ბუშტი არის სფერო, ბილიარდის ბურთი არის სრულფასოვანი ბურთი.
2. სფეროს აქვს ფართობი და არ აქვს მოცულობა, მაგრამ სფერო საპირისპიროს აკეთებს.
3. მესამე განსხვავება არის ორი გეომეტრიული სხეულის რადიუსის გაზომვა.

განმარტება.

სფერო შეიძლება შეფასდეს, როგორც სამგანზომილებიანი ფიგურა, რომელიც იქმნება მისი დიამეტრის გარშემო წრის 180°-ით ან ნახევარწრიული დიამეტრის გარშემო 360°-ით ბრუნვით.

განმარტება.

ბურთი შეიძლება შეფასდეს, როგორც სამგანზომილებიანი ფიგურა, რომელიც იქმნება მისი დიამეტრის გარშემო წრის 180°-ით ან მისი დიამეტრის გარშემო ნახევარწრიულის 360°-ით ბრუნვით.

განმარტება. სფეროს რადიუსი (ბურთი)(R) არის მანძილი სფეროს ცენტრიდან (ბურთი) ოსფეროს ნებისმიერ წერტილამდე (ბურთის ზედაპირი).

განმარტება. სფეროს (ბურთის) დიამეტრი(D) არის სეგმენტი, რომელიც აკავშირებს სფეროს ორ წერტილს (ბურთის ზედაპირს) და გადის მის ცენტრში.

ფორმულა. სფეროს მოცულობა:

ფორმულა. სფეროს ზედაპირის ფართობირადიუსის ან დიამეტრის მეშვეობით:

S = 4π R 2 = π D 2

სფეროს განტოლება

1. სფეროს განტოლება R რადიუსით და ცენტრით დეკარტის კოორდინატთა სისტემის სათავეში:

x 2 + y 2 + z 2 = R 2

2. სფეროს განტოლება რადიუსით R და ცენტრით წერტილში კოორდინატებით (x 0, y 0, z 0) დეკარტის კოორდინატულ სისტემაში:

(x - x 0) 2 + (y - y 0) 2 + (z - z 0) 2 = R 2

განმარტება. დიამეტრალურად საპირისპირო წერტილებიარის ნებისმიერი ორი წერტილი ბურთის (სფეროს) ზედაპირზე, რომლებიც დაკავშირებულია დიამეტრით.

სფეროსა და ბურთის ძირითადი თვისებები

1. სფეროს ყველა წერტილი ერთნაირად დაშორებულია ცენტრიდან.

2. სფეროს ნებისმიერი მონაკვეთი სიბრტყით არის წრე.

3. ბურთის ნებისმიერი მონაკვეთი სიბრტყით არის წრე.

4. სფეროს აქვს ყველაზე დიდი მოცულობა ერთნაირი ზედაპირის მქონე ყველა სივრცულ ფიგურას შორის.

5. ნებისმიერი ორი დიამეტრალურად საპირისპირო წერტილის მეშვეობით შეგიძლიათ დახაზოთ მრავალი დიდი წრე სფეროსთვის ან წრეები ბურთისთვის.

6. ნებისმიერი ორი წერტილის მეშვეობით, გარდა დიამეტრულად საპირისპირო წერტილებისა, შეგიძლიათ დახაზოთ მხოლოდ ერთი დიდი წრე სფეროსთვის ან დიდი წრე ბურთისთვის.

7. ერთი ბურთის ნებისმიერი ორი დიდი წრე იკვეთება სწორი ხაზის გასწვრივ, რომელიც გადის ბურთის ცენტრში და წრეები იკვეთება ორ დიამეტრალურად საპირისპირო წერტილზე.

8. თუ რომელიმე ორი ბურთის ცენტრებს შორის მანძილი ნაკლებია მათი რადიუსების ჯამზე და მეტია მათი რადიუსების სხვაობის მოდულზე, მაშინ ასეთი ბურთულები იკვეთება, და წრე გადაკვეთის სიბრტყეში იქმნება.

სფეროს სეკანტი, აკორდი, სეკანტური სიბრტყე და მათი თვისებები

განმარტება. სფეროს სეკანტიარის სწორი ხაზი, რომელიც კვეთს სფეროს ორ წერტილში. გადაკვეთის წერტილები ე.წ პირსინგის წერტილებიზედაპირები ან შესასვლელი და გასასვლელი წერტილები ზედაპირზე.

განმარტება. სფეროს აკორდი (ბურთი)- ეს არის სეგმენტი, რომელიც აკავშირებს ორ წერტილს სფეროზე (ბურთის ზედაპირი).

განმარტება. ჭრის თვითმფრინავიარის სიბრტყე, რომელიც კვეთს სფეროს.

განმარტება. დიამეტრული სიბრტყე- ეს არის სეკანტური სიბრტყე, რომელიც გადის სფეროს ან ბურთის ცენტრში, განყოფილება შესაბამისად იქმნება დიდი წრედა დიდი წრე. დიდ წრეს და დიდ წრეს აქვს ცენტრი, რომელიც ემთხვევა სფეროს (ბურთის) ცენტრს.

ნებისმიერი აკორდი, რომელიც გადის სფეროს (ბურთის) ცენტრში, არის დიამეტრი.

აკორდი არის სეგმენტური ხაზის სეგმენტი.

მანძილი d სფეროს ცენტრიდან სეკანტამდე ყოველთვის ნაკლებია სფეროს რადიუსზე:

დ< R

მანძილი m ჭრის სიბრტყესა და სფეროს ცენტრს შორის ყოველთვის ნაკლებია R რადიუსზე:

მ< R

ჭრის სიბრტყის მონაკვეთის მდებარეობა სფეროზე ყოველთვის იქნება პატარა წრე, და ბურთზე განყოფილება იქნება პატარა წრე. მცირე წრეს და პატარა წრეს აქვს საკუთარი ცენტრები, რომლებიც არ ემთხვევა სფეროს (ბურთის) ცენტრს. ასეთი წრის r რადიუსი შეგიძლიათ იხილოთ ფორმულის გამოყენებით:

r = √R 2 - მ 2,

სადაც R არის სფეროს (ბურთის) რადიუსი, m არის მანძილი ბურთის ცენტრიდან ჭრის სიბრტყემდე.

განმარტება. ნახევარსფერო (ნახევარსფერო)- ეს არის სფეროს (ბურთის) ნახევარი, რომელიც წარმოიქმნება დიამეტრული სიბრტყით მოჭრისას.

ტანგენსი, სფეროზე ტანგენსი სიბრტყე და მათი თვისებები

განმარტება. სფეროს ტანგენტიარის სწორი ხაზი, რომელიც ეხება სფეროს მხოლოდ ერთ წერტილში.

განმარტება. ტანგენტური სიბრტყე სფეროზეარის თვითმფრინავი, რომელიც ეხება სფეროს მხოლოდ ერთ წერტილში.

ტანგენტის ხაზი (სიბრტყე) ყოველთვის პერპენდიკულარულია შეხების წერტილამდე გამოყვანილი სფეროს რადიუსზე.

მანძილი სფეროს ცენტრიდან ტანგენტის ხაზამდე (სიბრტყე) უდრის სფეროს რადიუსს.

განმარტება. ბურთის სეგმენტი- ეს არის ბურთის ნაწილი, რომელიც მოწყვეტილია ბურთს საჭრელი თვითმფრინავით. სეგმენტის საფუძველიუწოდეს წრე, რომელიც ჩამოყალიბდა მონაკვეთის ადგილზე. სეგმენტის სიმაღლე h არის სეგმენტის ფუძის შუა ნაწილიდან სეგმენტის ზედაპირამდე დახატული პერპენდიკულარულის სიგრძე.

ფორმულა. სფეროს სეგმენტის გარე ზედაპირის ფართობი h სიმაღლით R სფეროს რადიუსში:

S = 2πRh