ボールの定義。 数学

ボールは、特定の点から特定の距離以下の距離にある空間内のすべての点で構成される物体です。 この点はボールの中心と呼ばれ、この距離はボールの半径と呼ばれます。 ボールの境界を球面または球と呼びます。 球の点は、中心から半径に等しい距離だけ離れたボールのすべての点です。 ボールの中心と球面上の点を結ぶ線分も半径と呼ばれます。 ボールの中心を通り、球面上の2点を結んだ線分を直径といいます。 任意の直径の端は、ボールの正反対の点と呼ばれます。

ボールは、円錐や円柱と同じように回転体です。 ボールは、その直径を軸として半円を回転させると得られます。

ボールの表面積は次の式で求められます。

ここで、r はボールの半径、d はボールの直径です。

ボールの体積は次の式で求められます。

V = 4 / 3 πr 3、

ここで、r はボールの半径です。

定理。 ボールの平面によるすべての部分は円です。 この円の中心は、ボールの中心から切断面に引いた垂線の底辺です。

この定理に基づいて、中心 O、半径 R のボールが平面 α と交差する場合、その断面は中心 K を持つ半径 r の円になります。平面によるボールの断面の半径は次のようになります。式で求めた

この公式から、中心から等距離にある平面がボールと等しい円で交差することがわかります。 断面の半径が大きいほど、切断面がボールの中心に近くなり、距離が小さくなるほど OK になります。 最大半径は、ボールの中心を通る平面による断面を有する。 この円の半径はボールの半径と同じです。

ボールの中心を通る平面を中心面といいます。 直径面による球の断面は大円と呼ばれ、球の断面は大円と呼ばれ、球の断面は大円と呼ばれます。

定理。 ボールの直径面はすべて対称面です。 ボールの中心が対称の中心です。

球面の点 A を通り、点 A に描かれた半径に垂直な平面を接平面と呼びます。 点Aを接点といいます。

定理。 接平面にはボールとの共通点が 1 つだけあり、それは接触点です。

球面の点Aを通り、そこに引く半径に垂直な直線を接線といいます。

定理。 無数の接線が球面上の任意の点を通過し、それらはすべてボールの接平面内にあります。

球セグメントは、ボールの一部を平面で切り取ったものです。 円 ABC は球形セグメントの底辺です。 円ABCの中心Nから球面との交点に引いた垂線MNが球面の高さになります。 点 M は球セグメントの頂点です。

球形セグメントの表面積は、次の式を使用して計算できます。

球状セグメントの体積は、次の式を使用して求めることができます。

V = πh 2 (R – 1/3h)、

ここで、R は大円の半径、h は球セグメントの高さです。

球形扇形は、次のように球形セグメントと円錐から得られます。 球状セグメントが半球よりも小さい場合、球状セグメントは円錐によって補完され、その頂点はボールの中心にあり、底面はセグメントの底面になります。 セグメントが半球より大きい場合は、指定された円錐が半球から削除されます。

球形セクターは、球形セグメントの曲面 (この図では AMCB) と円錐面 (この図では OABC) で囲まれたボールの一部であり、その底面が球面の底面です。セグメント (ABC) であり、頂点はボール O の中心です。

球状セクターの体積は次の式で求められます。

V = 2/3 πR 2 H。

球面層とは、球面と交差する２つの平行な面（図ではＡＢＣ面とＤＥＦ面）に挟まれたボールの一部である。 球面層の曲面を球面帯（ゾーン）と呼びます。 円ABCとDEFは球面ベルトの底辺です。 球面ベルトの底面間の距離 NK がその高さになります。

ウェブサイトのコンテンツの全部または一部をコピーする場合は、ソースへのリンクが必要です。

ボールと球はまず幾何学的図形であり、ボールが幾何学的な物体であれば、球はボールの表面です。 これらの数字は紀元前何千年も前から興味深いものでした。

その後、地球が球で空が天球であることが発見されたとき、幾何学の新しい興味深い方向性、つまり球上の幾何学または球面幾何学が開発されました。 ボールのサイズと体積について話すには、まずボールを定義する必要があります。

ボール

幾何学における点 O を中心とする半径 R の球は、共通の特性を持つ空間内のすべての点によって作成される物体です。 これらの点は、ボールの半径を超えない距離に配置されます。つまり、ボールの中心から全方向にボールの半径未満の空間全体を占めます。 ボールの中心から等距離にある点のみを考慮する場合は、ボールの表面またはシェルを考慮します。

どうすればボールを手に入れることができますか？ 紙から円を切り取り、その直径を中心に回転させ始めます。 つまり、円の直径が回転軸になります。 形成された図形はボールになります。 したがって、ボールは回転体とも呼ばれます。 平らな図形、つまり円を回転させることで形成できるからです。

飛行機に乗ってボールをカットしましょう。 ちょうどオレンジをナイフで切るのと同じように。 ボールから切り取った部分を球状セグメントと呼びます。

古代ギリシャでは、ボールや球を幾何学的図形として扱う方法、たとえば建築に使用する方法だけでなく、ボールの表面積やボールの体積を計算する方法も知っていました。

球とは、ボールの表面の別名です。 球は物体ではありません - それは回転体の表面です。 しかし、地球も多くの物体も、たとえば水滴などの球形をしているため、球内の幾何学的関係の研究が広く行われるようになりました。

たとえば、球の2点を直線で結んだ場合、この直線は弦と呼ばれ、この弦が球の中心（ボールの中心と一致する）を通過すると、その場合、弦は球の直径と呼ばれます。

球と一点だけで接する直線を引くと、この線は接線と呼ばれます。 さらに、この点での球の接線は、接触点に描かれた球の半径に対して垂直になります。

球面から一方向または別の方向に弦を直線に延長すると、この弦はセカントと呼ばれます。 あるいは、別の言い方をすることもできます。球の正割にはその弦が含まれています。

ボールの体積

ボールの体積を計算する公式は次のとおりです。

ここで、R はボールの半径です。

球状セグメントの体積を求める必要がある場合は、次の式を使用します。

Ｖ ｓｅｇ ＝πｈ ２ （Ｒ－ｈ／３）、ｈは球状セグメントの高さである。

ボールまたは球の表面積

球の面積またはボールの表面積を計算するには (これらは同じものです):

ここで、R は球の半径です。

アルキメデスはボールと球体がとても好きで、自分の墓に円筒の中にボールを刻んだ絵を残してほしいとさえ頼みました。 アルキメデスは、ボールの体積とその表面は、ボールが内接する円柱の体積と表面の 3 分の 2 に等しいと信じていました。」

ボール（球体）

球面。 ボール（球体）。 ボールセクション: サークル。

アルキメデスの定理。 ボールのパーツ: 球状セグメント、

球状層、球状ベルト、球状セクター。

球面 - これ 点の軌跡(それらの。 多くの全点の数)空間内で、一点から等距離にある ○ 、球面の中心と呼ばれます (図90)。 半径あおい 直径 AB 円と同じ方法で決定されます。

ボール（球体） - これ 球面で囲まれた物体。できる 半円を回転させてボールを取得します (またはサークル ）直径の周り。 ボールのすべての平面セクションは、 サークル (図90 ）。 最大の円はボールの中心を通る部分にあり、 大きな円。 その半径はボールの半径と同じです。 2 つの大きな円はボールの直径に沿って交差します ( AB、図91 ).この直径は、交差する大円の直径でもあります。 同じ直径の端にある球面の 2 点を通る(A と B、図 91 ）、大きな円を無数に描くことができます。 たとえば、地球の極を通る子午線は無限に引くことができます。

球の体積は、その周囲に外接する円柱の体積の 1.5 分の 1 です。 (図92 ), あ ボールの表面積は、同じ円柱の全表面積の 1.5 分の 1 です ( アルキメデスの定理):

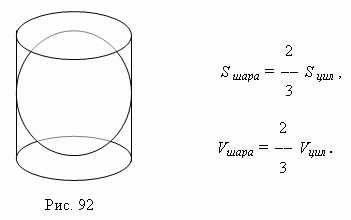
ここ S ボール そして V ボール - それぞれボールの表面と体積。

S シル そして V シル - 外接する円柱の総表面積と体積。

ボールのパーツ。 ボール（球体）の一部 )、何らかの平面によってそこから切り離されます ( ABC、図93)、 呼ばれた ボール(球状 ) セグメント。 サークルABC 呼ばれた 基礎ボールセグメント。 線分ミネソタ州 中心から引いた垂線 NサークルABC 球面と交わるまでを といいます。 身長ボールセグメント。 ドット M 呼ばれた 上ボールセグメント。

2 つの平行な平面の間に囲まれた球の一部球面と交差するABCとDEF(図93)、 呼ばれた 球状層; 球状層の曲面をといいます。 ボールベルト(ゾーン). サークル ABCとDEF – 根拠ボールベルト。 距離 N.K. 球状ベルトの基部の間 - その 身長。 球セグメントの曲面で囲まれたボールの部分 ( AMCB、 Fig.93) と円錐面 OABC 、そのベースがセグメントのベースになります ( ABC )、頂点はボールの中心です○ 、と呼ばれる 球状扇形.

球とボールの違いを尋ねられると、多くの人は単に肩をすくめ、実際には同じものだと考えます (円と円の類似)。 実際、私たち全員が学校のカリキュラムで幾何学をよく知っており、この質問にすぐに答えることができるでしょうか? 球にはボールとはいくつかの違いがあり、学童だけでなく、たとえば絵を描くことに直接関係する仕事をしている多くの人も、その知識を知っておく必要があります。

意味

ボール– 空間内のすべての点の集合。 これらすべての点は、幾何学的本体の中心から所定の距離以下の距離に位置します。 この距離自体を半径と呼びます。 幾何学的な物体としてのボールは次のように形成されます。半円がその直径近くで回転します。 球に関しては、これはボールの表面です (たとえば、閉じたボールにはそれが含まれますが、開いたボールには含まれません)。 ボールの面積または体積の計算には、幾何学図形自体の見かけの単純さにもかかわらず、非常に複雑な幾何学式全体が含まれます。

球上で述べたように、ボールの表面、つまりシェルです。 空間内のすべての点は球の中心から等距離にあります。 幾何学的ボディの半径に関しては、任意のセグメントと呼ばれ、その 1 つの点は球の中心に直接なり、もう 1 つは表面上の任意の点に配置できます。 球は内容のないボールの殻であると言えます (より具体的な例は以下に示します)。 ボールと同じように、球体も回転体です。 ちなみに、円と円、球とボールの違いは何なのか疑問に思う人も多いでしょう。 ここではすべてが単純です。最初の場合、これらは平面上の図であり、2番目の場合、空間内の図です。

比較

球はボールの表面であるとすでに述べましたが、これにより、違いの 1 つの重要な兆候について話すことができます。 2 つの幾何学的ボディの違いは、他のいくつかの側面でも観察されます。

• ボールのすべての点は中心から同じ距離にありますが、本体は表面 (内部が空の球) によって制限されています。 言い換えれば、球体は中空です。 通常、理解を容易にするために、風船とビリヤード ボールを使った簡単な例が示されます。 これらのオブジェクトはどちらもボールと呼ばれますが、前者の場合は球を扱い、後者の場合は内部に独自の内容を含む本格的なボールを扱います。
• 球には独自の面積がありますが、体積はありません。 球はその逆です。球には面積がありませんが、その体積は計算できます。 これが差異の主な兆候であると言う人もいるかもしれませんが、これは何らかの計算 (複雑な幾何学的公式) を行う必要がある場合にのみ表示されます。 したがって、主な違いは、球は中空であり、ボールは内部に内容物を含む本体であることです。
• もう一つの違いは半径にあります。 たとえば、球の半径は中心までの点の距離だけではありません。 半径は、球上の点をその中心に接続する任意のセグメントにすることができます。 これらすべてのセグメントは互いに等しい。 ボールに関しては、その内側にある点は中心から半径よりも小さく除去されます (正確には球が境界を定めているため)。

結論のウェブサイト

1. 球は中空ですが、ボールは内部が満たされた物体です。 たとえば、熱気球は球体、ビリヤードのボールは本格的なボールです。
2. 球には面積がありますが体積はありませんが、球はその逆です。
3. 3 番目の違いは、2 つの幾何学的ボディの半径の測定です。

意味。

球は、円をその直径の周りに 180 度回転させることによって、または半円をその直径の周りに 360 度回転させることによって形成される 3 次元の図形として説明できます。

意味。

ボールは、円を直径を中心に 180 度、または半円を直径を中心に 360 度回転して形成される 3 次元の図形として説明できます。

意味。 球（ボール）の半径(R)は球（ボール）の中心からの距離です。 ○球上の任意の点（ボールの表面）に。

意味。 球（ボール）の直径(D)は球(ボールの表面)の2点を結び、その中心を通る線分です。

式。 球体積:

式。 球の表面積半径または直径:

S = 4π R 2 = π D 2

球の方程式

1. デカルト座標系の原点を中心とし、半径が R の球の方程式:

x 2 + y 2 + z 2 = R 2

2. デカルト座標系の座標 (x 0, y 0, z 0) の点を中心とし、半径 R の球の方程式:

(x - x 0) 2 + (y - y 0) 2 + (z - z 0) 2 = R 2

意味。 正反対の点は、直径によって接続されたボール (球) の表面上の任意の 2 点です。

球とボールの基本的な性質

1. 球のすべての点は中心から等距離にあります。

2. 球の平面による断面はすべて円です。

3. ボールの平面による断面は円です。

4. 球体は、同じ表面積を持つすべての空間図形の中で最大の体積を持ちます。

5. 正反対の 2 つの点を介して、球の場合は大円を、またはボールの場合は円を多数描くことができます。

6. 正反対の点を除く任意の 2 点を通して、球の場合は大きな円を 1 つだけ、ボールの場合は大きな円を 1 つだけ描くことができます。

7. 1 つのボールの任意の 2 つの大円は、ボールの中心を通る直線に沿って交差し、円は正反対の 2 点で交差します。

8. 2 つのボールの中心間の距離がそれらの半径の合計より小さく、半径の差の係数より大きい場合、そのようなボールは 交差する、交差面に円が形成されます。

球の割線、弦、割面とその特性

意味。 球の割線は球と 2 点で交差する直線です。 交点は次のように呼ばれます。 ピアスポイントサーフェスまたはサーフェス上の入口点と出口点。

意味。 球（ボール）の弦- これは球 (ボールの表面) 上の 2 点を結ぶ線分です。

意味。 切断面球と交差する平面です。

意味。 直径面- これは球またはボールの中心を通過する割平面であり、それに応じて断面が形成されます。 大きな円そして 大きな円。 大円と大円の中心は球（ボール）の中心と一致します。

球 (ボール) の中心を通過する弦は直径です。

コードは割線のセグメントです。

球の中心から割線までの距離 d は、常に球の半径より小さくなります。

d< R

切断面と球の中心の間の距離 m は、常に半径 R より小さくなります。

メートル< R

球上の切断面の断面の位置は常に次のようになります。 小さな円、ボール上のセクションは次のようになります。 小さな円。 小円と小円はそれぞれ中心があり、球（ボール）の中心とは一致しません。 このような円の半径 r は、次の式を使用して求めることができます。

r = √R 2 - 平方メートル,

ここで、R は球 (ボール) の半径、m はボールの中心から切断面までの距離です。

意味。 半球（半球）- これは球 (ボール) の半分であり、直径方向の平面で切断すると形成されます。

球の接線、接平面とそのプロパティ

意味。 球の接線は球と一点だけで接する直線です。

意味。 球の接平面は球と一点だけで接する平面です。

接線(平面)は常に接点に描かれた球の半径に対して垂直になります。

球の中心から接線（平面）までの距離は球の半径と等しくなります。

意味。 ボールセグメント- これは、切断面によってボールから切り取られるボールの部分です。 セグメントの基礎セクションの場所に形成されたサークルと呼ばれます。 セグメントの高さ h は、セグメントの底面の中央からセグメントの表面に引いた垂線の長さです。

式。 球セグメントの外表面積球の半径 R を通る高さ h の場合:

S = 2πRh