機械波動公式の周波数の計算方法 v．発振周波数とは何ですか? 問題の例と解決策

地球上のあらゆるものには独自の周波数があります。あるバージョンによると、それは私たちの世界の基礎を形成しているとも言われています。残念ながら、この理論は 1 冊の出版物で紹介するには複雑すぎるため、独立した動作として振動の周波数のみを考慮します。この記事の枠組みの中で、この物理プロセス、その測定単位、および計測コンポーネントの定義が示されます。最後に、日常生活における普通の音の重要性の一例を考えてみましょう。私たちは彼が何者であり、彼の性質が何であるかを学びます。

発振周波数を何といいますか？

これは、周期的なプロセスを特徴付けるために使用される物理量を意味します。これは、1 単位時間内での特定のイベントの繰り返しまたは発生の数に相当します。この指標は、これらのインシデントの発生期間に対するインシデントの数の比率として計算されます。世界の各要素には独自の振動周波数があります。物体、原子、道路橋、電車、飛行機、それらはすべて特定の動きをしており、それをそう呼んでいます。これらのプロセスは目には見えませんが、存在します。発振周波数を計算する測定単位はヘルツです。それらの名前は、ドイツ出身の物理学者ハインリヒ・ヘルツに敬意を表して付けられました。

瞬時周波数

周期信号は、係数までの位相変化率である瞬間周波数によって特徴付けることができます。これは、独自の一定振動を持つ高調波スペクトル成分の合計として表すことができます。

サイクリック周波数

理論物理学、特に電磁気学のセクションで使用すると便利です。周期周波数 (半径方向、円周方向、角度方向とも呼ばれます) は、振動または回転運動の原点の強度を示すために使用される物理量です。 1 つ目は、1 秒あたりの回転数または振動数で表されます。回転運動中、周波数は角速度ベクトルの大きさに等しくなります。

この指標はラジアン/秒で表されます。周期周波数の次元は時間の逆数です。数値的には、2π 秒間に発生した振動または回転の数に等しくなります。これを導入すると、エレクトロニクスや理論物理学のさまざまな範囲の公式を大幅に簡素化することができます。最も一般的な使用例は、発振 LC 回路の共振周期周波数を計算することです。他の式は大幅に複雑になる可能性があります。

離散イベントレート

この値は、単位時間内に発生する離散的なイベントの数に等しい値を意味する。理論的には、通常使用される指標は 2 から 1 乗を引いたものです。実際には、通常、パルス周波数を表すためにヘルツが使用されます。

回転周波数

これは、単位時間内に発生する完全な回転数に等しい物理量として理解されます。ここで使用される指標も、2 乗から 1 乗を引いたものです。行われた仕事量を示すには、分、時間、日、月、年などの回転数などの表現を使用できます。

単位

発振周波数はどのように測定されますか? SI システムを考慮する場合、ここでの測定単位はヘルツです。もともとは 1930 年に国際電気標準会議によって導入されました。そして、1960 年の第 11 回度量衡総会では、この指標の SI 単位としての使用が統合されました。「理想」として掲げられたものは何でしょうか？ 1秒で1サイクルが完了する周波数です。

しかし、生産についてはどうでしょうか？キロサイクル、メガサイクル/秒などの任意の値が割り当てられました。したがって、GHz で動作するデバイス (コンピュータープロセッサなど) を手に取ると、それが実行するアクションの数を大まかに想像できます。人の時間の流れはとてもゆっくりと感じられるでしょう。しかし、このテクノロジーは、同じ期間内に 1 秒あたり数百万、さらには数十億の操作を実行することができます。 1 時間の間に、コンピューターはすでに非常に多くのアクションを実行しているため、ほとんどの人はそれらを数値的に想像することさえできません。

計量学的側面

発振周波数は計測学にも応用されています。さまざまなデバイスには多くの機能があります。

パルス周波数が測定されます。電子計数方式とコンデンサ方式で代表されます。
スペクトル成分の周波数が決定されます。ヘテロダイン型と共振型があります。
スペクトル解析が行われます。
必要な周波数を所定の精度で再現します。この場合、標準、シンセサイザー、信号発生器、およびこの方向の他の技術など、さまざまな手段を使用できます。
得られた振動の指標は比較され、この目的にはコンパレータまたはオシロスコープが使用されます。

作品例：音

上に書いたことはすべて、物理学の無味乾燥な言語を使用したため、理解するのが非常に難しい場合があります。提供される情報を理解するために、例を挙げることができます。現代生活の事例の分析に基づいて、すべてが詳細に説明されます。これを行うには、振動の最も有名な例である音を考えてみましょう。その特性、および媒体内での機械的弾性振動の実装の特徴は、周波数に直接依存します。

人間の聴覚器官は、20 Hz ～ 20 kHz の範囲の振動を検出できます。また、年齢とともに上限は徐々に下がっていきます。音の振動の周波数が 20 Hz (mi 下請けに相当) を下回ると、超低周波音が発生します。このタイプは、ほとんどの場合、私たちには聞こえませんが、人々は触覚で感じることができます。 20 キロヘルツの制限を超えると、超音波と呼ばれる振動が発生します。周波数が 1 GHz を超える場合、この場合はハイパーサウンドを扱います。ピアノなどの楽器を考えると、27.5 Hz から 4186 Hz の範囲の振動が発生する可能性があります。楽音は基本周波数だけで構成されているわけではなく、倍音や倍音も混合されていることに注意してください。これらすべてが音色を決定します。

結論

皆さんも学ぶ機会があったように、振動周波数は私たちの世界が機能するために非常に重要な要素です。彼女のおかげで、私たちは彼女の支援によってコンピュータが動作し、その他多くの有用なことが達成されたと聞くことができます。しかし、発振周波数が最適限界を超えると、特定の破壊が始まる可能性があります。したがって、クリスタルが 2 倍のパフォーマンスで動作するようにプロセッサに影響を与えると、すぐに故障してしまいます。

同様のことが人間の生命にも言え、高周波で鼓膜が破裂することがあります。他にも体にマイナスの変化が起こり、特定の問題、さらには死に至ることもあります。さらに、物理的な性質の特殊性により、このプロセスはかなり長期間に渡って続きます。ちなみに、この要素を考慮して、軍は将来の兵器を開発するための新たな機会を検討しています。

1. 機械波、波の周波数。縦波と横波。

2. 波面。スピードと波長。

3. 平面波方程式。

4. 波のエネルギー特性。

5. いくつかの特殊な種類の波。

6. ドップラー効果と医療におけるその利用。

7. 表面波の伝播中の異方性。生体組織に対する衝撃波の影響。

8. 基本的な概念と公式。

9. タスク。

2.1. 機械波、波の周波数。縦波と横波

弾性媒体（固体、液体、気体）のどこかでその粒子の振動が励起されると、粒子間の相互作用により、この振動は媒体中を粒子から粒子へと一定の速度で伝播し始めます。 v.

たとえば、振動体が液体または気体の媒体中に置かれる場合、振動体の振動運動は、それに隣接する媒体の粒子に伝達されます。さらに、隣接する粒子を振動運動などに巻き込みます。この場合、媒体のすべての点は同じ周波数、つまり物体の振動周波数と同じで振動します。この周波数はと呼ばれます 波の周波数。

波弾性媒体内で機械的振動が伝播するプロセスです。

波の周波数は、波が伝播する媒体の点の振動の周波数です。

波は、振動源から媒体の周辺部分への振動エネルギーの伝達に関連しています。同時に、環境の中で次のようなことが起こります。

波によって媒質内のある点から別の点に伝わる周期的な変形。媒体の粒子自体は波とともに移動しませんが、平衡位置の周りで振動します。したがって、波動の伝播は物質の移動を伴いません。

周波数に応じて、機械波はさまざまな範囲に分けられ、表にリストされています。 2.1.

表2.1。メカニカルウェーブスケール

波の伝播方向に対する粒子の振動の方向に応じて、縦波と横波が区別されます。

縦波- 波。伝播中に媒体の粒子が波の伝播と同じ直線に沿って振動します。この場合、圧縮領域と希薄化領域が媒体内で交互に現れます。

縦方向の機械波が発生する可能性がある 全部で媒体（固体、液体、気体）。

横波- 波。伝播中に粒子が波の伝播方向に対して垂直に振動します。この場合、媒体内で周期的なせん断変形が発生します。

液体や気体では、弾性力は圧縮時にのみ発生し、せん断時には発生しないため、これらの媒体では横波は形成されません。例外は、液体表面の波です。

2.2. 波面。速度と波長

自然界には、無限の高速で伝播するプロセスは存在しないため、媒体内のある点での外部の影響によって生じた撹乱は、すぐに別の点に到達するのではなく、しばらくしてから到達します。この場合、媒質は 2 つの領域に分割されます。1 つは点がすでに振動運動に関与している領域、もう 1 つは点が平衡状態にある領域です。これらの領域を分離する表面はと呼ばれます 波面。

波面 -振動（媒質の摂動）がこの瞬間に到達する点の幾何学的軌跡。

波が伝播するとき、その前面は一定の速度で移動しますが、これを波速といいます。

波の速度 (v) は、その前線が移動する速度です。

波の速度は、媒体の特性と波の種類によって異なります。固体内の横波と縦波は異なる速度で伝播します。

あらゆる種類の波の伝播速度は、波の減衰が弱い条件下で次の式で求められます。

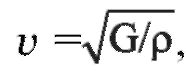ここで、G は有効弾性率、ρ は媒体の密度です。

媒質中の波の速度を、波の過程に関与する媒質の粒子の移動速度と混同しないでください。例えば、音波が空気中を伝播するとき、その分子の平均振動速度は約10cm/s、通常の状態での音波の速度は約330m/sです。

波面の形状によって、波の幾何学的タイプが決まります。これに基づく最も単純なタイプの波は次のとおりです。 フラットそして 球状。

フラットは、その正面が伝播方向に垂直な平面である波です。

平面波は、たとえば、ガスが入った閉じたピストンシリンダー内でピストンが振動するときに発生します。

平面波の振幅は実質的に変化しません。波源からの距離に応じてそのわずかな減少は、液体または気体の媒体の粘度に関連しています。

球状前面が球の形をしている波と呼ばれます。

これは、たとえば、脈動する球状の源によって液体または気体の媒体中に引き起こされる波です。

球面波の振幅は、音源からの距離に応じて、距離の二乗に反比例して減少します。

干渉や回折などの多くの波動現象を説明するには、波長と呼ばれる特別な特性が使用されます。

波長は、媒体の粒子の振動周期に等しい時間内にその前面が移動する距離です。

ここ v- 波の速度、T - 振動周期、 ν - 媒体内の点の振動の周波数、 ω - サイクリック周波数。

波の伝播速度は媒質の性質に依存するため、波長は λ ある環境から別の環境に移動するときの頻度は変化しますが、 ν 同じまま。

この波長の定義には重要な幾何学的解釈があります。図を見てみましょう。 2.1 a。ある時点での媒体内の点の変位を示します。波面の位置は点 A と B でマークされます。

1 振動周期に等しい時間 T が経過すると、波面が移動します。その位置は図に示されています。 2.1、b は A 1 と B 1 を指します。図からわかるように、波長は λ これは、同じ位相で振動する隣接する点間の距離、たとえば、外乱の 2 つの隣接する最大値または最小値間の距離に等しい。

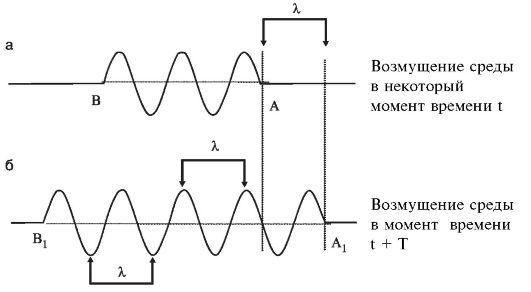米。 2.1.波長の幾何学的解釈

2.3. 平面波方程式

波は、環境に対する定期的な外部影響の結果として発生します。配分を考える フラット音源の調和振動によって生成される波:

ここで、x とは音源の変位、A は振動の振幅、ω は振動の円周周波数です。

媒質内の特定の点が音源から距離 s 離れていて、波の速度が次の場合、 v、その場合、発生源によって生成された外乱は、時間 τ = s/v 後にこの点に到達します。したがって、時刻 t における問題の点の振動の位相は、時刻における音源の振動の位相と同じになります。 (t - s/v)、そして振動の振幅は実質的に変化しません。結果として、この点の振動は次の方程式によって決定されます。

ここでは円周波数の公式を使用しました。 (ω = 2π/T) と波長 (λ = vた）。

この式を元の式に代入すると、次のようになります。

式 (2.2) は、いつでも媒体内の任意の点の変位を決定するものと呼ばれます。 平面波方程式。コサインの引数は大きさです φ = ωt - 2 π s /λ - 呼ばれた 波の位相。

2.4. 波のエネルギー特性

波が伝播する媒体には機械的エネルギーがあり、これはすべての粒子の振動運動のエネルギーの合計です。質量 m 0 の 1 つの粒子のエネルギーは、式 (1.21) に従って求められます。 E 0 = m 0 Α 2ω 2/2。媒体の単位体積には n = が含まれます。 p/m 0 粒子 (ρ - 媒体の密度)。したがって、媒体の単位体積はエネルギー w р = nЕ 0 = を持ちます。 ρ Α 2ω 2 /2.

体積エネルギー密度(\\р) - 単位体積に含まれる媒質の粒子の振動運動のエネルギー:

ここで、ρ は媒体の密度、A は粒子振動の振幅、ω は波の周波数です。

波が伝播するにつれて、波源によって与えられたエネルギーが遠くの領域に伝達されます。

エネルギー伝達を定量的に説明するために、次の量が導入されます。

エネルギーの流れ(F) - 単位時間当たりに与えられた表面を通って波によって伝達されるエネルギーに等しい値:

波の強さまたはエネルギー束密度 (I) - 波の伝播方向に垂直な単位面積を通って波によって伝達されるエネルギー束に等しい値。

波の強度は、その伝播速度と体積エネルギー密度の積に等しいことがわかります。

2.5. いくつかの特別な品種

波

1. 衝撃波。音波が伝播するとき、粒子の振動速度は数 cm/s を超えません。それは波の速度の数百分の１です。強い外乱（爆発、超音速での物体の動き、強力な放電）下では、媒体の振動粒子の速度が音速に匹敵することがあります。これにより、衝撃波と呼ばれる効果が発生します。

爆発中、高温に加熱された高密度製品は膨張し、周囲の空気の薄い層を圧縮します。

衝撃波 -超音速で伝播する薄い遷移領域。この領域では、圧力、密度、物質の移動速度が急激に増加します。

衝撃波はかなりのエネルギーを持つ可能性があります。したがって、核爆発中、総爆発エネルギーの約 50% が環境内での衝撃波の形成に費やされます。衝撃波は物体に到達し、破壊を引き起こす可能性があります。

2. 表面波。連続媒体中の実体波に加えて、拡張された境界が存在する場合、境界付近に局在する波が存在する可能性があり、これが導波管の役割を果たします。これらは、特に、19 世紀の 90 年代に英国の物理学者 W. ストラット (レイリー卿) によって発見された、液体および弾性媒体中の表面波です。理想的な場合、レイリー波は半空間の境界に沿って伝播し、横方向に指数関数的に減衰します。その結果、表面波は、表面上で生じた擾乱のエネルギーを比較的狭い表面近くの層に局所化します。

表面波 -物体の自由表面に沿って、または物体の他の媒体との境界に沿って伝播し、境界からの距離とともに急速に減衰する波。

このような波の例としては、地殻内の波（地震波）があります。表面波の侵入深さは数波長です。波長 λ に等しい深さでは、波の体積エネルギー密度は表面での体積密度の約 0.05 になります。変位振幅は表面から離れるにつれて急速に減少し、数波長の深さで事実上消失します。

3. 活性媒体中の励起波。

積極的に興奮可能な環境、またはアクティブな環境は、それぞれがエネルギーを蓄えている多数の要素で構成される連続的な環境です。

この場合、各要素は 3 つの状態のいずれかになります: 1 - 励起、2 - 不応性 (励起後の一定時間非励起性)、3 - 静止。元素は静止状態からのみ励起されます。活性媒体中の励起波は自己波と呼ばれます。 オートウェーブ -これらは活性媒体中で自立する波であり、媒体中に分散されたエネルギー源によりその特性を一定に維持します。

定常状態における自動波の特性 (周期、波長、伝播速度、振幅、形状) は、媒質の局所的な特性にのみ依存し、初期条件には依存しません。テーブル内 2.2 は、自動波と通常の機械波の類似点と相違点を示しています。

オートウェーブは、草原での火災の広がりにたとえることができます。炎はエネルギーが分散された領域 (乾いた草) に広がります。後続の各要素 (乾いた草の葉) は、前の要素から点火されます。したがって、励起波 (炎) の前面は活性媒体 (乾いた草) を通って伝播します。 2つの火が出会うと、エネルギー貯蔵量が使い果たされ、草がすべて燃え尽きるため、炎は消えます。

活性媒体における自己波の伝播プロセスの説明は、神経および筋線維に沿った活動電位の伝播を研究するために使用されます。

表2.2。オートウェーブと通常のメカニカルウェーブの比較

2.6. ドップラー効果と医療におけるその利用

クリスチャン・ドップラー (1803-1853) - オーストリアの物理学者、数学者、天文学者、世界初の物理学研究所の所長。

ドップラー効果振動の発生源と観察者の相対的な動きにより、観察者が知覚する振動の周波数の変化で構成されます。

この効果は音響と光学で観察されます。

波の発信源と受信機が、それぞれ速度 v I と v P で同じ直線に沿って媒体に対して移動する場合のドップラー効果を説明する式を取得しましょう。 ソース平衡位置に対して周波数 ν 0 の調和振動を実行します。これらの振動によって生成された波は、媒体中をある速度で伝播します。 v.この場合、どのような周波数の振動が記録されるかを調べてみましょう。 受信機。

ソースの振動によって発生した外乱は、媒体を通って伝播し、受信機に到達します。時間 t 1 = 0 で始まる、ソースの 1 つの完全な振動を考えてみましょう。

そして、t 2 = T 0 の瞬間に終了します（T 0 はソースの発振周期です）。これらの瞬間に生じた環境の乱れは、それぞれ瞬間 t" 1 と t" 2 で受信機に到達します。この場合、受信機は周期と周波数の発振を記録します。

発信元と受信機が動いている場合の瞬間 t" 1 と t" 2 を求めてみましょう。 に向かってそれらの間の初期距離は S に等しくなります。t 2 = T 0 の時点で、この距離は S - (v И + v П)T 0 に等しくなります (図 2.2)。

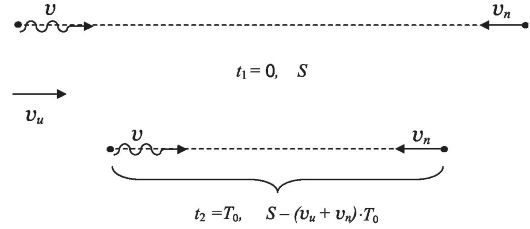米。 2.2.時刻 t 1 および t 2 における発信源と受信機の相対位置

この公式は、速度 v と v p が方向付けられている場合に有効です。 に向かってお互い。一般的に引っ越しの際には、

ソースとレシーバーを 1 つの直線に沿って配置すると、ドップラー効果の公式は次の形式になります。

ソースの速度 v And は、受信機の方向に移動する場合は「+」記号で取得され、そうでない場合は「-」記号で取得されます。受信機の場合も同様です（図2.3）。

米。 2.3.波の発信元と受信機の速度の標識の選択

ドップラー効果を医療に使用する特殊なケースを 1 つ考えてみましょう。超音波発生器を、媒体に対して固定された何らかの技術システムの形で受信機と組み合わせるとします。発生器は周波数 ν 0 の超音波を放射し、超音波は速度 v で媒体中を伝播します。 に向かってある物体が速度vtの系で動いている。まずシステムが役割を実行します ソース (v AND= 0)、本体は受信者の役割です (vTL=vT)。その後、波は物体から反射され、固定受信装置によって記録されます。この場合、v И = vT、そしてv p = 0。

式 (2.7) を 2 回適用すると、放射信号の反射後にシステムによって記録される周波数の式が得られます。

で 近づいてくる反射信号のセンサー周波数に対するオブジェクト 増加し、そしていつ 除去 - 減少します。

ドップラー周波数シフトを測定すると、式 (2.8) から反射体の移動速度を求めることができます。

「+」記号は、エミッターに向かう体の動きに対応します。

ドップラー効果は、血流の速度、心臓の弁と壁 (ドップラー心エコー検査) およびその他の器官の動きの速度を測定するために使用されます。血流速度を測定するための対応する設備の図を図に示します。 2.4.

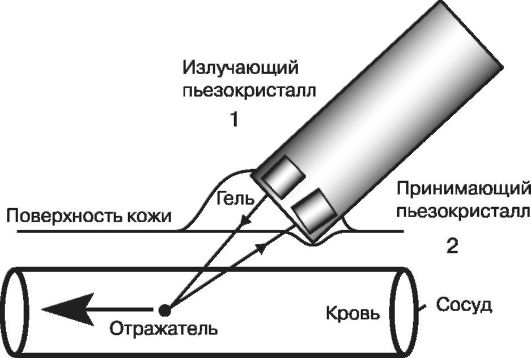米。 2.4.血流速度を測定するための設置図: 1 - 超音波源、2 - 超音波受信機

この装置は 2 つの圧電結晶で構成され、1 つは超音波振動 (逆圧電効果) の生成に使用され、もう 1 つは血液によって散乱された超音波 (直接圧電効果) を受信するために使用されます。

例。超音波の逆反射を利用して動脈内の血流速度を測定します。 (ν 0 = 100 kHz = 100,000 Hz、 v = 1500 m/s) 赤血球からドップラー周波数シフトが発生します νD = 40 Hz。

解決。式 (2.9) を使用すると、次のようになります。

v 0 = v D v /2v0 = 40バツ 1500/(2バツ 100,000) = 0.3 m/秒。

2.7. 表面波の伝播中の異方性。生体組織に対する衝撃波の影響

1. 表面波伝播の異方性。周波数 5 ～ 6 kHz の表面波 (超音波と混同しないでください) を使用して皮膚の機械的特性を研究すると、皮膚の音響異方性が現れます。これは、物体の垂直 (Y) 軸と水平 (X) 軸に沿った、互いに垂直な方向における表面波の伝播速度が異なるという事実で表されます。

音響異方性の深刻度を定量化するには、次の式で計算される機械的異方性係数が使用されます。

どこ vy- 垂直軸に沿った速度、 vx- 水平軸に沿って。

次の場合、異方性係数は正 (K+) として扱われます。 vy> vxで vy < vx係数は負 (K -) として扱われます。肌における表面波の速度や異方性の度合いを数値化したものは、肌をはじめとするさまざまな効果を評価するための客観的な基準となります。

2. 生体組織に対する衝撃波の影響。生体組織（器官）への衝撃の多くの場合、その衝撃波を考慮する必要があります。

たとえば、鈍器が頭に当たると衝撃波が発生します。したがって、保護ヘルメットを設計する際には、正面衝突の際に衝撃波を吸収し、後頭部を保護するように注意が払われます。この目的はヘルメットの内側のテープによって実現されますが、一見すると換気のためだけに必要であるように見えます。

組織が高強度のレーザー放射にさらされると、組織内で衝撃波が発生します。多くの場合、この後、皮膚に瘢痕 (またはその他) の変化が生じ始めます。これは、たとえば美容処置の際に起こります。したがって、衝撃波の有害な影響を軽減するには、放射線と皮膚自体の物理的特性を考慮して、事前に被ばく線量を計算する必要があります。

米。 2.5.放射状衝撃波の伝播

衝撃波は放射状衝撃波療法に使用されます。図では、図 2.5 は、アプリケーターからの放射状衝撃波の伝播を示しています。

このような波は、特別なコンプレッサーを備えたデバイスで作成されます。放射状の衝撃波は空気圧方式で生成されます。マニピュレータ内にあるピストンは、制御された圧縮空気パルスの影響を受けて高速で動きます。ピストンがマニピュレーターに取り付けられたアプリケーターに衝突すると、その運動エネルギーが衝撃を受けた体の領域の機械エネルギーに変換されます。この場合、アプリケーターと皮膚の間にある空隙での波の伝達時の損失を減らし、衝撃波の良好な伝導性を確保するために、コンタクトジェルが使用されます。通常動作モード: 周波数 6 ～ 10 Hz、動作圧力 250 kPa、セッションあたりのパルス数 - 最大 2000。

1. 船上で、霧の中で信号を発するサイレンがオンになり、t = 6.6 秒後にエコーが聞こえます。反射面までの距離はどれくらいですか? 空気中の音速 v= 330 m/秒。

解決

時間 t で、音は 2S の距離を進みます: 2S = vt →S = vt/2 = 1090 m。 答え：南＝1090メートル。

2. コウモリが 100,000 Hz センサーを使用して検出できる物体の最小サイズはどれくらいですか? イルカが 100,000 Hz の周波数を使用して検出できる物体の最小サイズはどれくらいですか?

解決

物体の最小寸法は波長に等しくなります。

λ1= 330 m/s / 10 5 Hz = 3.3 mm。これはコウモリが餌とする昆虫のサイズとほぼ同じです。

λ2= 1500 m/s / 10 5 Hz = 1.5 cm イルカは小魚を感知できます。

答え：λ1= 3.3 mm; λ2= 1.5cm。

3. まず、人は稲妻の閃光を目にし、8秒後に雷鳴が聞こえます。彼からどのくらいの距離で稲妻が光りましたか?

解決

S = v スター t = 330 バツ 8 = 2640 メートル。 答え： 2640メートル。

4. 2 つの音波は、一方の波長が他方の 2 倍であることを除いて、同じ特性を持っています。どちらがより多くのエネルギーを運ぶでしょうか？何回ですか？

解決

波の強度は周波数の二乗 (2.6) に正比例し、波長の二乗に反比例します。 (ω = 2πv/λ ). 答え：波長が短いもの。 4回。

5. 周波数 262 Hz の音波は空気中を 345 m/s の速度で伝わります。 a) その波長は何ですか? b) 空間内の特定の点での位相が 90°変化するのにどれくらい時間がかかりますか? c) 6.4 cm 離れた点間の位相差 (度) はいくらですか?

解決

A) λ = v /ν = 345/262 = 1.32 メートル;

V) Δφ = 360°s/λ= 360 バツ 0.064/1.32 = 17.5°。 答え： A) λ = 1.32メートル; b) t = T/4; V) Δφ = 17.5°。

6. 伝播速度がわかっている場合、空気中の超音波の上限 (周波数) を推定します。 v= 330 m/秒。空気分子のサイズが d = 10 -10 m 程度であると仮定します。

解決

空気中では、機械波は縦方向であり、波長は分子の最も近い 2 つの濃度（または希薄化）の間の距離に対応します。凝縮間の距離は決して分子のサイズよりも小さくすることはできないため、d = λ. これらの考慮事項から、 ν = v /λ = 3,3バツ 10～12Hz。 答え：ν = 3,3バツ 10～12Hz。

7. 2 台の車が速度 v 1 = 20 m/s および v 2 = 10 m/s で互いに向かって移動しています。最初のマシンは、ある周波数の信号を発します。 ν 0 = 800Hz。音速 v= 340 m/秒。 2 番目の車のドライバーはどの周波数の信号を聞くことになりますか: a) 車が合流する前。 b) 車が合流した後?

8. 列車が通過すると、汽笛の周波数が ν 1 = 1000 Hz (列車が近づくとき) から ν 2 = 800 Hz (列車が遠ざかるとき) に変化するのが聞こえます。電車の速度はどれくらいですか?

解決

この問題は、音源 (電車) の速度が分からず、その信号の周波数 ν 0 が分からないという点で、前の問題とは異なります。したがって、2 つの未知数を含む連立方程式が得られます。

解決

させて v・風速、人（受信機）から音源に向かって吹きます。それらは地面に対して静止していますが、空気に対しては両方とも速度 u で右に移動します。

式 (2.7) を使用して、音の周波数を取得します。人によって認識される。変更されていません:

答え：周波数は変わりません。

周期的に繰り返される動きを振動と呼びます。したがって、振動中の物体の座標と速度の時間依存性は、時間の周期関数によって記述されます。学校の物理の授業では、物体の依存関係や速度が三角関数である振動を考えます。 , またはそれらの組み合わせ。ここで、は特定の数です。このような振動は調和(関数)と呼ばれます。そしてしばしば調和関数と呼ばれます)。物理の統一国家試験のプログラムに含まれる振動の問題を解くには、振動の振幅、周期、周波数、円周波 (または周期) 周波数、位相といった振動運動の主な特性の定義を知る必要があります。これらの定義を与え、リストされた量を物体座標の時間依存性のパラメーターと結び付けましょう。調和振動の場合、これは常に次の形式で表すことができます。

ここで、とは数値です。

振動の振幅は、振動体の平衡位置からの最大偏差です。 (11.1) の余弦の最大値と最小値は ±1 に等しいため、(11.1) で振動する本体の振動の振幅はに等しくなります。振動周期とは、物体の動きが繰り返される最小時間です。依存関係(11.1)の場合、以下の点を考慮して期間を設定できます。コサインは周期を伴う周期関数です。したがって、このような値を通じて動作が完全に繰り返されます。ここから得られるのは、

振動の円周 (または周期) 周波数は、単位時間あたりに実行される振動の数です。式 (11.3) から、円周波数は式 (11.1) の量であると結論付けられます。

振動位相は、時間に対する座標の依存性を表す三角関数の引数です。式 (11.1) から、依存性 (11.1) によってその動きが記述される物体の振動の位相は、次と等しいことがわかります。。時間 = 0 における発振位相の値は、初期位相と呼ばれます。依存性 (11.1) の場合、振動の初期位相はに等しい。明らかに、振動の初期位相は時間基準点 (モーメント = 0) の選択に依存しますが、これは常に条件付きです。時間の原点を変更することで、振動の初期位相を常にゼロに「変える」ことができ、式 (11.1) のサインをコサインに「変換」したり、その逆を行うことができます。

統一国家試験のプログラムには、ばねの振動数の公式と数学的な振り子の知識も含まれています。ばね振り子は通常、ばねの作用により滑らかな水平面上で振動できる本体と呼ばれ、その第 2 端は固定されています (左の図)。数学的な振り子は、その寸法が無視できる巨大な物体であり、無重力で伸縮性のない長い糸の上で振動します (右図)。このシステムの名前「数学振り子」は、抽象的なものを表すという事実に由来しています。 数学的実際のモデル ( 物理的な) 振り子。ばねの振動の周期（または周波数）と数学的な振り子の公式を覚えておく必要があります。スプリング振り子の場合

ここで、は糸の長さ、は重力加速度です。問題解決の例を使用して、これらの定義と法則の適用を考えてみましょう。

負荷の振動の周期周波数を求めるには タスク11.1.1まず振動の周期を求めて、式(11.2)を使いましょう。 10m28sは628sであり、この間に負荷が100回振動するので、負荷の振動周期は6.28sとなります。したがって、振動の周期周波数は 1 s -1 (答え 2 ）。で 問題11.1.2負荷は 600 秒間に 60 回振動したため、振動周波数は 0.1 秒 -1 になります (答え) 1 ).

荷物が 2.5 周期で移動する距離を理解するには ( 問題11.1.3）、彼の動きを追ってみましょう。一定期間が経過すると、荷重は最大たわみ点に戻り、完全な振動が完了します。したがって、この間、荷重は 4 つの振幅に等しい距離を移動します。平衡位置まで - 1 つの振幅、平衡位置から他の方向の最大偏差点まで - 2 つ目、平衡位置に戻る - 3番目、平衡位置から開始点まで - 4番目。 2 番目の期間では、負荷は再び 4 つの振幅を通過し、期間の残りの半分では 2 つの振幅を通過します。したがって、移動距離は 10 振幅に等しくなります (答え 4 ).

体の移動量は始点から終点までの距離です。 2.5期以上 タスク11.1.4体には完全な振動を 2 回半完了する時間があります。は最大偏差になりますが、平衡位置の反対側にあります。したがって、変位の大きさは 2 つの振幅に等しくなります (答え 3 ).

定義により、振動の位相は、振動体の座標の時間依存性を記述する三角関数の引数です。したがって、正しい答えは、 問題11.1.5 - 3 .

周期とは、完全に振動する時間のことです。これは、体が動き始めた同じ点に戻ることは、一定期間が経過したことを意味するわけではないことを意味します。体は同じ速度で同じ点に戻らなければなりません。たとえば、平衡位置から振動を開始した物体には、一方向に最大量逸脱して元に戻り、他の方向に最大量逸脱して再び元に戻る時間があります。したがって、この期間中、体は平衡位置から最大量だけ逸れてから元に戻る時間が2回あります。したがって、平衡位置から最大偏差点までの経過 ( 問題11.1.6) 体は周期の 4 分の 1 を費やします (答え 3 ).

調和振動は、振動体の座標の時間依存性が時間の三角関数 (サインまたはコサイン) で表される振動です。で タスク11.1.7これらは関数とですが、それらに含まれるパラメータは 2 と 2 として指定されています。この関数は時間の二乗の三角関数です。したがって、量だけの振動と調和振動です（答え 4 ).

調和振動中、物体の速度は法則に従って変化します。ここで、は速度振動の振幅です (時間基準点は振動の初期位相がゼロに等しくなるように選択されます)。ここから、体の運動エネルギーの時間依存性がわかります。
(問題11.1.8）。よく知られている三角関数の公式をさらに使用すると、次のようになります。

この式から、調和振動中に物体の運動エネルギーも調和の法則に従って変化しますが、周波数が 2 倍になることがわかります (答え) 2 ).

荷重の運動エネルギーとばねの位置エネルギーの関係の背後にある ( 問題11.1.9) は、次の考慮事項から簡単に理解できます。物体が平衡位置から最大量だけたわむとき、物体の速度はゼロであるため、ばねの位置エネルギーは負荷の運動エネルギーよりも大きくなります。逆に、物体が平衡位置を通過するとき、ばねの位置エネルギーはゼロであるため、運動エネルギーは位置エネルギーよりも大きくなります。したがって、平衡位置を通過してから最大たわみに達するまでの間に、運動エネルギーと位置エネルギーが 1 回比較されます。そして、物体は 1 周期の間に 4 回平衡位置から最大たわみまで、またはその逆に通過するため、その期間中、荷重の運動エネルギーとばねの位置エネルギーが 4 回比較されます (答え) 2 ).

速度変動の振幅 ( タスク11.1.10) は、エネルギー保存則を使用して見つけるのが最も簡単です。最大たわみ点では、振動系のエネルギーはばねの位置エネルギーに等しくなります。、ここで、はバネの剛性係数、は振動振幅です。平衡位置を通過するとき、体のエネルギーは運動エネルギーに等しいここで、は物体の質量、は平衡位置を通過するときの物体の速度であり、これは振動プロセス中の物体の最大速度であり、したがって速度振動の振幅を表します。これらのエネルギーを同等にすると、次のようになります。

（答え 4 ).

式 (11.5) から次の結論が得られます ( 問題11.2.2)、その周期は数学的な振り子の質量に依存せず、長さが 4 倍増加すると、振動の周期は 2 倍増加します (答え 1 ).

時計は、時間の間隔を測定するために使用される振動プロセスです ( 問題11.2.3）。「時計が急いでいる」という言葉は、このプロセスの時間が本来よりも短いことを意味します。したがって、これらのクロックの進み具合を明確にするには、処理の周期を長くする必要があります。式(11.5)によれば、振り子の振動周期を長くするには、振り子の長さを長くする必要があります(答え) 3 ).

振動の振幅を求めるには、 問題11.2.4、身体座標の時間依存性を単一の三角関数の形式で表す必要があります。条件で指定された関数については、追加の角度を導入することでこれを行うことができます。この関数を乗算および除算すると、三角関数を追加する公式を使用すると、次のようになります。

そのような角度はどこですか。この式から、物体振動の振幅は次のようになります。（答え 4 ).

調和振動は、サインとコサインの法則に従って行われる振動です。次の図は、余弦の法則に従った、時間の経過に伴う点の座標の変化のグラフを示しています。

写真

発振振幅

調和振動の振幅は、平衡位置からの物体の変位の最大値です。振幅はさまざまな値をとることができます。それは、最初の瞬間に体を平衡位置からどれだけ変位させるかによって決まります。

振幅は初期条件、つまり最初の瞬間に身体に与えられるエネルギーによって決まります。サインとコサインは -1 から 1 までの範囲の値を取ることができるため、方程式には振動の振幅を表す係数 Xm が含まれている必要があります。調和振動の運動方程式:

x = Xm*cos(ω0*t)。

発振周期

振動の周期は、1 つの完全な振動が完了するまでにかかる時間です。振動の周期は文字 T で示されます。周期の測定単位は時間の単位に対応します。つまり、SI では秒です。

発振周波数は、単位時間当たりに実行される発振の数です。発振周波数は文字 ν で示されます。発振周波数は発振周期で表すことができます。

ν = 1/T。

周波数の単位は SI 1/秒です。この測定単位はヘルツと呼ばれます。 2*pi 秒間の振動数は次のようになります。

ω0 = 2*pi* ν = 2*pi/T。

発振周波数

この量は振動の周期周波数と呼ばれます。一部の文献では、循環周波数という名前が表示されます。振動系の固有周波数は、自由振動の周波数です。

固有振動の周波数は、次の式を使用して計算されます。

固有振動の周波数は、材料の特性と負荷の質量によって異なります。ばねの剛性が大きいほど、ばね自身の振動の周波数も大きくなります。負荷の質量が大きくなるほど、固有振動の周波数は低くなります。

これら 2 つの結論は明らかです。スプリングが硬ければ硬いほど、システムのバランスが崩れたときに体に加わる加速度は大きくなります。物体の質量が大きいほど、この物体の速度の変化は遅くなります。

自由発振期間:

T = 2*pi/ ω0 = 2*pi*√(m/k)

小さい偏向角では、ばね上の本体の振動周期と振り子の振動周期が振動の振幅に依存しないことは注目に値します。

数学的な振り子の自由振動の周期と周波数の公式を書き留めてみましょう。

そうすれば期間は等しくなります

T = 2*pi*√(l/g)。

この式は、偏向角が小さい場合にのみ有効です。式から、振り子の糸の長さが増加すると、振動周期が増加することがわかります。長さが長いほど本体の振動は遅くなります。

振動の周期は負荷の質量にはまったく依存しません。ただし、それは自由落下の加速度に依存します。 g が減少すると、発振周期は増加します。この性質は実際に広く使用されています。たとえば、自由加速度の正確な値を測定します。

線速度は均一に方向を変えるため、円運動は均一とは言えず、均一に加速されます。

角速度

円上の点を選択しましょう 1 。半径を構築しましょう。単位時間内に、点は点に移動します 2 。この場合、半径は角度を表します。角速度は、数値的には単位時間あたりの半径の回転角度に等しくなります。

期間と頻度

自転周期 T- これは、体が 1 回転する時間です。

回転数とは、1秒あたりの回転数のことです。

周波数と周期は次の関係にあります。

角速度との関係

線速度

円上の各点は一定の速度で移動します。この速度を線形と呼びます。 線速度ベクトルの方向は常に円の接線と一致します。たとえば、研削盤の下からの火花は瞬間的な速度の方向を繰り返しながら移動します。

1 回転する円上の点を考えます。費やした時間が周期です。 T。点が移動する経路が円周です。

向心加速度

円内を移動する場合、加速度ベクトルは常に速度ベクトルに対して垂直になり、円の中心に向かって方向を向きます。

前述の式を使用すると、次の関係を導き出すことができます。

円の中心から伸びる同じ直線上にある点 (たとえば、これらは車輪のスポーク上にある点である可能性があります) は、同じ角速度、周期、および周波数を持ちます。つまり、同じ方向に回転しますが、線速度は異なります。点が中心から離れるほど、その点の移動速度は速くなります。

速度の加算の法則は回転運動にも当てはまります。物体または基準系の動きが均一でない場合、この法則は瞬間速度に適用されます。たとえば、回転するカルーセルの端に沿って歩く人の速度は、カルーセルの端の回転の線形速度と人の速度のベクトル和に等しくなります。

地球は、日周運動 (地軸の周り) と軌道運動 (太陽の周り) という 2 つの主な回転運動に参加します。地球が太陽の周りを一周する周期は1年または365日です。地球は地軸の周りを西から東に回転し、この回転の周期は 1 日または 24 時間です。緯度は、赤道面と地球の中心から地表上の点に向かう方向との間の角度です。

ニュートンの第 2 法則によれば、加速度の原因は力です。移動体が向心加速度を経験する場合、この加速度を引き起こす力の性質は異なる可能性があります。たとえば、物体がそれに結び付けられたロープの上を円を描くように動く場合、作用する力は弾性力です。