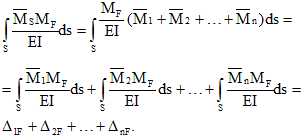Számítsunk ki egy lapos statikailag határozatlan rúdrendszert! Statikailag határozatlan rendszerek számítása erőmódszerrel

Az erőmódszer kanonikus egyenletei

Számítási algoritmus erőmódszerrel

Az elsődleges rendszer kiválasztása

Kanonikus egyenletek együtthatóinak és szabad tagjának számítása

A kanonikus egyenletek együtthatóinak és szabad feltételeinek univerzális ellenőrzése

A statikusan határozatlan rendszerek olyan rúdrendszerek, amelyekben az egyensúlyi egyenletek önmagukban nem elegendőek a hordozók reakcióinak meghatározásához. Kinematikai szempontból ezek olyan rúdrendszerek, amelyek szabadsági foka kisebb, mint a kapcsolatok száma. Az ilyen rendszerek statikus határozatlanságának feltárásához további egyenleteket kell alkotni az alakváltozások kompatibilitására. Az ilyen egyenletek számát a rúdrendszer statikus határozatlansági száma határozza meg. A 8.14. ábra statikusan határozatlan gerendákra és keretekre mutat példákat.

A 8.14b ábrán látható gerendát ún folyamatos gerenda. Ez az elnevezés onnan ered, hogy a közbenső támasz csak a gerendát támasztja alá. Az alátámasztási ponton a gerendát nem vágja be a csuklópánt, a csuklópánt nincs belevágva a gerenda testébe. Ezért a gerenda bal oldali fesztávon fellépő feszültségek és deformációk hatása a jobb fesztávra is hatással van. Ha a közbenső támasz helyén csuklópántot vágunk a gerenda testébe, akkor ennek eredményeként a rendszer statikailag meghatározott lesz - egy gerendából két egymástól független gerendát kapunk, amelyek mindegyike statikailag meghatározott lesz. . Megjegyzendő, hogy a folytonos gerendák kevésbé anyagigényesek, mint az osztott gerendák, mivel racionálisabban osztják el a hajlítónyomatékokat hosszuk mentén. Ebben a tekintetben a folytonos gerendákat széles körben használják az építőiparban és a gépészetben. A folytonos gerendák azonban, mivel statikailag határozatlanok, speciális számítási technikát igényelnek, amely magában foglalja a rendszer deformációit is.

A statikusan határozatlan rendszerek számításának megkezdése előtt meg kell tanulni, hogyan határozható meg statikus határozatlanságuk mértéke. A statikus határozatlanság mértékének meghatározásának egyik legegyszerűbb szabálya a következő:

, (8.3)

Ahol  a szerkezetre kifejtett kapcsolatok száma;  a vizsgált rendszerre összeállítható lehetséges független egyensúlyi egyenletek száma.

Használjuk a (8.3) egyenletet a 8.14. ábrán látható rendszerek statikus határozatlanságának mértékére.

A 8.14a ábrán látható gerenda egyszer statikusan határozatlan, mivel három csatlakozása van a bal tartón és egy csatlakozás a jobb tartón. Egy ilyen nyalábra csak három független egyensúlyi egyenlet szerkeszthető. Így a sugár statikus határozatlanságának mértéke
. A 8.14b ábrán látható folytonos gerenda is egyszer statikailag határozatlan, mivel két csatlakozása van a bal oldali tartón és egy-egy csatlakozása a közbenső tartón és a jobb oldali tartón - összesen négy csatlakozás. Így a statikus határozatlanságának mértéke
.

ábrán látható keret. 8.14c, háromszor statikailag határozatlan, mivel hat csatlakozása van a tartókban. Ehhez a kerethez csak három független egyensúlyi egyenlet szerkeszthető. Így ennek a keretnek a statikus meghatározatlansági foka a (8.3) egyenletből egyenlő:
. A 8.18d ábrán látható keret statikus határozatlanságának mértéke négy, mivel a keret hét csatlakozással rendelkezik a tartókon. Következésképpen a statikus határozatlanságának mértéke egyenlő
.

A statikus határozatlanság mértékének meghatározására szolgáló (8.3) szabály csak egyszerű rendszerekre vonatkozik. Bonyolultabb esetekben ez a szabály nem működik. A 8.15. ábrán egy keret látható, amelynek statikus határozatlanságának mértéke nem határozható meg a (8.3) egyenlettel.

Külsőleg a 8.15. ábrán látható rendszer ötször statikusan határozatlan. Ez könnyen megállapítható a (8.3) egyenlettel: hat külső kapcsolatból (három az A szakaszban, három a B szakaszban és kettő a C részben) három lehetséges egyensúlyi egyenletet vonunk le. Ennek a rendszernek azonban van belső statikus határozatlansága is. A belső statikus meghatározatlanságot nem lehet figyelembe venni a (8.3) egyenlet segítségével. Mielőtt rátérnénk a 8.15. ábrán látható keret statikus határozatlanság fokának meghatározására, bemutatunk néhány definíciót. A meghatározások közül az első tartalmazza az egyszerű csuklópánt fogalmát.

Egyszerű két rudat összekötő csuklópántnak nevezzük (8.16. ábra).

8.16. ábra. Egyszerű zsanér

Több rudat összekötő csuklópántot nevezünk összetett(8.17. ábra).

8.17. ábra. Komplex zsanér

Az egy összetett csuklópánt helyettesítésére alkalmas egyszerű zsanérok számát a képlet határozza meg:

, (8.4)

Ahol
- a szerelvényben lévő rudak száma.

Számítsuk át a 8.17. ábrán látható összetett csuklópántot az egyszerű csuklópántok számára a (8.4) képlet segítségével:
. Így a 8.17. ábrán látható összetett zsanér négy egyszerű csuklópánttal helyettesíthető.

Mutassunk be még egy fogalmat - zártláncú.

Bizonyítsuk be a tételt: bármely zárt körvonal háromszor statikailag határozatlan.

A tétel bizonyításához tekintsünk egy külső erőkkel terhelt zárt hurkot (8.18. ábra).

Vágjunk egy zárt kontúrt függőleges metszettel, és mutassuk be a metszetnél fellépő belső erőtényezőket. Mindegyik szakaszban három belső tényező lép fel: a nyíróerő , hajlítási nyomaték
és hosszanti erő
. Összességében a kontúr minden egyes levágott részén a külső erők mellett hat belső tényező hat (8.18. ábra, b, c). Figyelembe véve az egyik levágott rész egyensúlyát, például a bal oldali (8.18. ábra, b), azt találjuk, hogy a feladat háromszoros statikailag határozatlan, mivel a levágott részre konstruálható csak három független egyensúlyi egyenlet, és hat ismeretlen erő hat a levágási részre. Így egy zárt hurok statikus határozatlanságának mértéke egyenlő
. A tétel bizonyítást nyert.

Most az egyszerű csuklópánt és a zárt hurok fogalmát használva megfogalmazhatunk egy másik szabályt a statikus határozatlanság mértékének meghatározására:

, (8.5)

Ahol
 zárt hurkok száma;
 zsanérok száma az egyszerűeknél (8,4).

A (8.5) egyenlet segítségével meghatározzuk a 8.15. ábrán látható keret statikus határozatlanságának mértékét. A keretnek öt kontúrja van
, beleértve a tartórudak által alkotott kontúrt. A D csomópont csuklópántja egyszerű, mivel két rudat köt össze. A K szakasz csuklópántja összetett, mert négy rudat köt össze. Azon egyszerű zsanérok száma, amelyek helyettesíthetik a csuklópántot a K szakaszban, egyenlő a (8.4) képlet szerint:
. A C csukló azért is összetett, mert három rudat köt össze. Ehhez a zsanérhoz
. Ezen kívül a rendszernek van még két egyszerű zsanérja, amelyekkel az alaphoz rögzíthető. Így a rendszerben lévő egyszerű csuklópántok száma egyenlő
. A zárt kontúrok számának helyettesítése
és az egyszerű zsanérok száma
a (8.5) képletben meghatározzuk a keret statikus határozatlanságának mértékét:
. Így az ábrán látható. 8,15 képkocka, hétszer statikusan határozatlan. Ez azt jelenti, hogy egy ilyen rendszer kiszámításához a három egyensúlyi egyenlet mellett hét alakváltozási kompatibilitási egyenletet kell összeállítani. Az így kapott 10-es egyenletrendszer megoldásával az egyenletekben szereplő ismeretlenekre, meghatározható mind a külső kapcsolatokban fellépő reakciók nagysága, mind a keretben fellépő belső erők mértéke. A probléma megoldásának eljárása némileg leegyszerűsíthető, ha az egyensúlyi egyenleteket kivesszük az egyenletrendszerből. Ez a megközelítés azonban speciális megoldási módszerek alkalmazását igényli, amelyek közül az egyik az erők módszere.

Statikailag határozatlan rendszerek azok a rendszerek, amelyekben a belső erők nem határozhatók meg csak az egyensúlyi egyenletekből (statikus egyenletek).

A statikailag határozatlan szerkezetek ún külön- kommunikáció. Előfordulhatnak tartókban, rudakban és más elemekben. Az ilyen kapcsolatokat „feleslegesnek” nevezik, mivel nem szükségesek a szerkezet egyensúlyának biztosításához, hanem a szilárdságra és merevségre vonatkozó követelmények határozzák meg. Az ilyen extra kapcsolatokat ún külső. Ezenkívül szükségtelen csatlakozások is felmerülhetnek magának a tervezésnek a sajátosságai miatt. Például egy zárt keret kontúr (46. ábra, G) minden szakaszában három ismeretlen belső erő van, pl. összesen hat van, és ebből három „extra”. Ezt az extra erőfeszítést ún belső. A külső vagy belső „extra” kapcsolatok száma alapján létesítenek a rendszer statikus határozatlanságának mértéke. Ez egyenlő a meghatározandó ismeretlenek száma és a statikus egyenletek száma közötti különbséggel. Egy „extra” ismeretlennel a rendszer egyszer, vagy egyszer statikusan határozatlannak, kettővel – kétszer statikusan határozatlannak stb.

ábrán látható kialakítás. 46, A, egyszer statikailag határozatlan, és az ábrán látható szerkezetek. 46, bÉs V, - kétszer statikailag határozatlan, az ábrán. 46, g - háromszor statikailag határozatlan szerkezettel.

Statikailag határozatlan feladatok megoldásánál a statikai egyenletek mellett olyan egyenleteket alkalmaznak, amelyek figyelembe veszik a szerkezeti elemek alakváltozásait.

Számos módszer létezik a statikusan határozatlan problémák megoldására: elmozdulás összehasonlító módszer, erő módszer, elmozdulás módszer.

Kényszer módszer

Statikailag határozatlan rendszerek kiszámításakor az erőket ismeretlennek tekintjük.

Számítás szerint erő módszer a következő sorrendben hajtjuk végre:

1. Határozza meg a statikus határozatlanság mértékét!
2. Az „extra” kapcsolatok eltávolításával cserélje ki az eredeti rendszert egy statikusan meghatározhatóra, ún. fő rendszer. Több ilyen rendszer is megépíthető, figyelemmel a földrajzi helyzetükre

metrikus megváltoztathatatlanság.

3. A fő rendszert adott külső erők és „extra” ismeretlen erők terhelik, amelyek helyettesítik a távoli kapcsolatok működését, ami egyenértékű rendszer.
4. Az eredeti és a főrendszer egyenértékűségének biztosítása érdekében az ismeretlen erőket úgy kell megválasztani, hogy a főrendszer alakváltozásai ne térjenek el az eredeti statikailag határozatlan rendszer alakváltozásaitól. Az alkalmazási pontok ilyen mozgásához a működésük irányában lévő „extra” ismeretlenek nullával egyenlőek. Az így kapott további egyenletek alapján meghatározzák az „extra” ismeretlen erőfeszítések értékeit. A megfelelő pontok elmozdulásának meghatározása bármilyen módon elvégezhető, de célszerű a legáltalánosabb Mohr-módszert használni.
5. Az „extra” ismeretlen erők értékeinek meghatározása után meghatározzuk a reakciókat és elkészítjük a belső erők diagramjait, kiválasztjuk a metszeteket és a szokásos módon ellenőrizzük a szilárdságot.

Az erőmódszer kanonikus egyenletei

Az „extra” ismeretlenek irányában az elmozdulás nullával való egyenlőségét kifejező további eltolási egyenletek kényelmesen összeállíthatók az ún. kanonikus forma, azok. egy bizonyos minta szerint. Mutassuk meg ezt a legegyszerűbb statikailag határozatlan rendszer megoldásának példáján (47. ábra, A).

Fő rendszernek válasszuk a konzolt, a zsanértámaszt elvetve. Egy ekvivalens rendszert kapunk a T 7 külső erő és az „extra” ismeretlen alkalmazása után x(47. ábra, b).

Kanonikus egyenlet, amely a ponteltolódás egyenlőségét fejezi ki nullával BAN BEN F erőitől X, akarat

A rendelkezésünkre álló egyenletből

Egy két „extra” kapcsolattal rendelkező rendszer esetében a kanonikus egyenletrendszer a következőképpen alakul:

8 11 X 1 + b 12 ^2 + ^1
621-^1 + 622^2 "I" ^20-

Mozdulatok A[r A kanonikus egyenletekben szereplő b[y-t pedig Mohr módszerével határozzuk meg.

Az egyenes vonalú elemekből álló rendszerek esetében kényelmes az elmozdulások kiszámítása Vereschagin módszerével.

ábrán látható probléma esetén például. A 47. ábra diagramjait megszorozva (48. ábra) megkapjuk a kanonikus egyenlet együtthatóit:

1 2 I 3 1 I/I 2 1 5 I1 3

E]b LL =-/ / -/ = -, E]A LR =-------- +-------.

1 11 2 3 3 1 1Р 2 2 2 2 3 2/ 48 E]

Kapunk Hl - - = - E.

Miután meghatározta az erőt X, valóban megtaláltuk a támogató reakciót Én benne vagyok. Ezután a belső erőtényezők meghatározásának problémája a szokásos módon megoldható a metszet módszerrel.

AZ OROSZ Föderáció OKTATÁSI MINISZTÉRIUMA

KORMÁNYINTÉZMÉNY

KUZBASS ÁLLAMI MŰSZAKI EGYETEM

Anyagszilárdsági Osztály

SZTATIKUSAN MEGHATÁROZOTT SZÁNTRUDA RENDSZEREK KISZÁMÍTÁSA FESZÜLTSÉG ALATT

Útmutató a számítási és grafikai feladatok anyagerősségen történő elvégzéséhez minden szakos hallgató számára

Összeállította: V.D. Moiseenko

Tanszéki ülésen jóváhagyva Jegyzőkönyv 2001. június 29-i 8. sz

Egy elektronikus példány a KuzSTU Állami Egyetem főépületének könyvtárában található

Kemerovo 2002

Bevezetés. A megbízás köre és célja

Statikailag határozatlan csuklórúd rendszer az, amelyben a pálcákban fellépő erők és a tartókban zajló reakciók nem határozhatók meg csak az egyensúlyi állapotból.

Az 1. ábra egy hagyományos konzolt mutat, amely két rúdból áll. Az N 1 és N 2 erők ennek a tartónak a rúdjaiban könnyen meghatározhatók a kivágott C csomópontra ható konvergáló erőrendszer egyensúlyi állapotából, mivel erre az erőrendszerre két egyenlet két ismeretlennel van megoldva.

Ha a konzol kialakítását bonyolítja egy másik rúd hozzáadása (1. ábra, b), akkor a pálcákban lévő erők nem határozhatók meg ugyanúgy, mivel a C csomópontra továbbra is csak két statikus egyensúlyi egyenletet lehet létrehozni ( ΣХ = 0; ΣY = 0), és az ismeretlen erőfeszítések száma három. Van egy egyszer statikusan határozatlan rendszerünk.

A tervezés bonyolításával és új rudak bevezetésével kétszer (lásd 1. ábra c), háromszor stb. lehet statikailag határozatlan rendszert kapni. Következésképpen n-szeres statikusan határozatlan rendszer alatt olyan rendszert értünk, amelyben a kapcsolatok száma n egységgel meghaladja a független statikus egyenletek számát.

A probléma megoldásához szükséges további egyenletek a rendszer deformált állapotának figyelembevételével és a szerkezeti elemek elmozdulásai és alakváltozásai közötti összefüggések megállapításával kereshetők meg. Az így kapott egyenleteket deformációs kompatibilitási egyenleteknek nevezzük.

A 2. ábrán néhány statikusan határozatlan rendszer diagramja látható.

2. ábra. A statikusan határozatlan rendszerek bizonyos típusai

A „Statikusan határozatlan rúdrendszerek” fejezet tanulmányozása és a számítási és grafikai feladat elvégzése során a hallgatónak meg kell tanulnia a statikusan határozatlan rendszerek jellemzőit; készségeket szerezni a statikus határozatlanság feltárásában, a szerkezeti elemekben lévő erők meghatározásában és a szilárdsági viszonyokból keresztmetszeti területek kiválasztásában.

A feladatban a hallgatónak az alábbi feladatokat kell elvégeznie:

- határozza meg a rudak erőit, és válassza ki a keresztmetszeti területeket a külső terhelések hatására;

- meghatározza a hőmérsékletváltozások miatti további feszültségeket a rudaknál;

- a rudak pontatlan gyártása által okozott további beépítési feszültségek meghatározása;

- válasszuk ki a rudak keresztmetszeteit a határállapotnak megfelelően.

A számítási és grafikai feladat végrehajtásának volumene és formája a tanult tárgy mennyiségétől függ, és a gyakorlati órákon a tanár megbeszéli.

1. Rövid elméleti információk

Statikailag határozatlan feladatok megoldásánál a következő sorrendet kell követni:

1.1. Tekintsük a probléma statikus oldalát. Készítsen erőtervet és alkosson statikus egyenleteket.

1.2. Tekintsük a probléma geometriai oldalát. Készítsen utazási tervet. Hozzon létre további alakváltozás-kompatibilitási egyenleteket olyan mennyiségben, hogy minden ismeretlen erő megtalálható legyen.

1.3. Vegye figyelembe a probléma fizikai oldalát. A fizika törvényei szerint (hőmérséklet-számításoknál) és Hooke törvénye szerint fejezze ki a deformációkat kompatibilitási egyenletekben a rudakba ható ismeretlen erők révén:

∆l t =α ∆t l	∆l N =
		E.F.

1.4. Végezze el a statika, geometria, fizika egyenletek együttes megoldását, és határozza meg az ismeretlen erőket!

1.5. Nyomó- vagy szakítószilárdsági feltételek alkalmazása N/F = [σ], válassza ki a rudak keresztmetszeti területeit.

1.6. A rudak ismert erőivel és elfogadott keresztmetszeti területekkel számítsa ki a normál feszültségeket a képlet segítségével

σ = N F .

2. Példa

Adott: Abszolút merev AB gerenda van megtámasztva, a 3. ábrán látható módon, egyenletesen elosztott P terheléssel és erővel terhelve.

3. ábra. Statikailag határozatlan rendszer diagramja

Kiinduló adatok a számításhoz

Anyag

[σ ]Р ,

[σ] SJ,

α ,

F ST

2 105

125 10-7

1 105

165 10-7

Kívánt:

Határozza meg az erőket (N CT; N M), a keresztmetszeti területeket (F CT;

F M) és feszültség (σ C r T; σ M r) acél (ST) és réz (M) rúd-

nyakh P és q külső terhelések hatására.

;σ М t

Határozza meg a rudak további feszültségeit (σ ST t

∆ t = + 20 o C hőmérsékletváltozástól.

Határozza meg a rudak által okozott járulékos feszültségeket

pontatlanság a függőleges rúd gyártásánál ∆ = 0,1 cm.

4. Határozza meg a terhelések, hőmérséklet-változások és gyártási pontatlanságok miatt a rudak összes feszültségét.

2.1. Statikailag határozatlan csuklós rúdrendszer számítása külső terhelésre

P = 30 kN q = 15 kN/m

A C B

4. ábra. Kezdeti számítási séma

2.1.1. A probléma statikus oldala

A probléma statikus oldalát az erőterv veszi figyelembe. Az erőterv egy számítási diagram, amely bemutatja a csuklórúd-rendszer azon elemére ható összes erőt (az ismert és ismeretlen), amelynek egyensúlyát vizsgáljuk (esetünkben ez az AB merev gerenda). Vágjuk le az acél- és rézrudakat, és belső erőkkel pótoljuk kidobott alsó részeiket (5. ábra).

P = 30 kN q = 15 kN/m

A C B

60°

	a =2 m
N st
		B = 4 m

Rizs. 5. Külső terhelésből származó erők terve

Az erőtervből (lásd 5. ábra) írjuk fel a statikus egyensúly egyenleteit. A probléma első kérdésének megválaszolásához ismernie kell a rudak - acél és réz - erőit. Ebben az esetben nem kell számolni a csuklós rögzített támasz reakcióját. Ezért a háromból

lehetséges statikus egyenleteket (ΣX = 0; ΣY = 0; Σm c = 0) írjuk fel

amely nem tartalmazza a csuklós-rögzített támasz reakcióit C:

∑ mC = 0

− N CT a + q a 2 2 + p a + NM sin60o b = 0,

− N ST 2 + 15 2 2 2 + 30 2 − NM 0,866 4 = 0,

Az algebrai műveletek után az egyensúlyi egyenlet alakot ölt

NCT + 1,73 NM = 45.

2.1.2. A probléma geometriai oldala

A probléma geometriai oldalát az eltolási terv veszi figyelembe. Az elmozdulási terv egy számítási diagram, amely bemutatja a csuklópánt-rúd rendszer helyzetét terhelés előtt és után. A mozgástervben feltüntetjük a nyalábpontok mozgását (AA1 és BB1),

réz- és acélrudak abszolút alakváltozásai (∆ l ST; ∆ l M)

(6. ábra). Sőt, a kis alakváltozások miatt a gerendapontokat függőlegesen felfelé vagy lefelé mozgatjuk, a ferde rudak alakváltozásait pedig merőlegesen jelöljük.

		60°

∆l st
∆l st		∆l m
		∆l m

	4 m
	4 m

Rizs. 6. Külső terhelések miatti elmozdulások terve

Az eltolási terv segítségével elkészítjük az alakváltozás-kompatibilitási egyenletet. Először is írjuk fel a gerenda pontjainak elmozdulásának arányát az AA1 C és CBB1 háromszögek hasonlóságából (6. ábra):

A gerenda pontjainak (AA1 és BB1) elmozdulásait alakváltozásokkal fejezzük ki

rudak (∆ l CT; ∆ l M):
AA1 = ∆ l ST
A BB1 B2 háromszögből a következőket fejezzük ki:
BB=	B1 B2	∆l M
BB=	sin60o	sin60o.
	sin60o	sin60o.

A (2.3) és (2.4) kifejezéseket behelyettesítjük a (2.2) relációba:


∆ lCT sin 60o

∆l M

	∆ lCT 0,866
		∆l M

		0,866 ∆ lST =	0,5∆ lМ.
Ez az egyenlet
		deformációs kompatibilitás.

2.1.3. A probléma fizikai oldala

Az így kapott (2.5) alakváltozási kompatibilitási egyenlet ebben a formában nem oldható meg a (2.1) egyensúlyi egyenlettel, mert a bennük szereplő ismeretlen mennyiségek eltérő jellegűek.

A (2.5) egyenletben szereplő ∆ l CT és ∆ l M abszolút alakváltozások kifejezhetők

a rudakban lévő erők révén a Hooke-törvény szerint:

∆l =

N ST l ST

NM lМ

E ST F ST

E M F M

Helyettesítsük be a kezdeti adatok számértékeit, és fejezzük ki az F ST-t

F M-ig a kiindulási adatok szerint:

F ST

4, ahonnan F ST = 4 F M = 0,75 F M,

NST 1,2

NM 1.9

és megkapjuk

105 0,75 F

1105 F

Az aritmetikai műveletek elvégzése után a következőket kapjuk:

0,67NCT = 0,95 NM.

Az alakváltozások kompatibilitási egyenletét kaptuk, amelyet a rudak erőivel írtunk fel.

2.1.4. Szintézis

Oldjuk meg együtt a (2.1) egyensúlyi egyenletet és a (2.6) deformációs kompatibilitási egyenletet.

NCT + 1,73 NM = 45

0,67NCT = 0,95 NM.

A rendszer második egyenletéből kifejezzük az N ST erőt:

N ST +		NM = 1,42 NM

és behelyettesítjük a rendszer első egyenletébe.

Az N ST és N M pozitív eredménye megerősíti az acélrúd összenyomására és a rézrúd feszültségére vonatkozó feltételezéseinket, ami azt jelenti, hogy a rudak erői:

NST = –20,3 kN;

NM = 14,3 kN.

2.1.5. A rudak keresztmetszete kiválasztása

A rudak keresztmetszete kiválasztását a szakítószilárdság - összenyomódás feltételei szerint végezzük:

N F ≤ [σ] .

a) Meghatározzuk az acélrúd szilárdsági állapotból szükséges keresztmetszeti területét:

N ST

≥ 1,7 10− 4

[ σ ST ] tömörít

F ST

Ráadásul az adott területarány szerint

4 terület

réz rúdnak egyenlőnek kell lennie:

4 1,7 10− 4

2,27 10− 4

b) Meghatározzuk a rézrúd szilárdsági állapotból szükséges keresztmetszeti területét:

Ebben az esetben az adott területaránynak megfelelően az acélrúd területének egyenlőnek kell lennie:

FST = 4 3 FM = 4 3 1,7 10−4 = 1,275 10−4 m2 ..

Nagy keresztmetszetű rudakat fogadunk el:

FST = 1,7 10−4 m2;

FM = 2,27 10−4 m2.

A réz- és acélrudak elfogadott keresztmetszeti területeit figyelembe véve meghatározzuk ezekben a rudak feszültségeit.

		N ST	− 20,3 10− 3 MN		= −119,4 MPa,
				1,7 10− 4 m2
		F ST
	p N M			14,3 10−3 MN	63 MPa.
σМ =				2,27 10− 4 m2

2.2. Statikailag határozatlan csuklórúd rendszer hőmérséklet számítása

A hőmérsékletszámítás célja a réz- és acélrudakban a hőmérséklet-változások miatti további feszültségek meghatározása.

Tegyük fel, hogy a rendszer ∆ t = 20 o C-kal melegszik fel. A megoldási algoritmus változatlan marad. A kezdeti tervezési diagram a ábrán látható. 7.

Az olyan rúdrendszereket, támaszreakciókat és belső erőtényezőket nevezzük, amelyekben nem lehet pusztán egyensúlyi egyenletekből megállapítani statikailag határozatlan.

Az ismeretlen erők száma és a független egyensúlyi egyenletek közötti különbség határozza meg a rendszer statikus határozatlanságának mértéke. A statikus határozatlanság mértéke mindig megegyezik a redundáns (felesleges) kapcsolatok számával, amelyek eltávolításával egy statikailag határozatlan rendszer statikailag meghatározható geometriailag megváltoztathatatlan rendszerré válik. Mind a külső (támasztó) csatlakozások, mind a belsőek redundánsak lehetnek, bizonyos korlátozásokat szabva a rendszerszakaszok egymáshoz viszonyított mozgására.

Geometriailag megváltoztathatatlan olyan rendszer, amelynek alakja csak elemeinek deformációi miatt változhat.

Geometriailag változó olyan rendszer, amelynek elemei külső erők hatására deformáció nélkül mozoghatnak (mechanizmus).

ábrán látható. 12.1 a keret hét külső (támasztó) hivatkozással rendelkezik. Az ezekben az összefüggésekben (támasztóreakciókban) fellépő erők meghatározásához mindössze három független egyensúlyi egyenletet hozhat létre. Ebből következően ennek a rendszernek négy redundáns kapcsolata van, ami azt jelenti, hogy négyszer statikusan határozatlan. Így a lapos keretek statikus határozatlanságának mértéke egyenlő:

Ahol R- támogató reakciók száma.

Zártnak nevezzük azt a körvonalat, amely több (egyenes vagy ívelt) elemből áll, amelyek mereven (csuklópántok nélkül) kapcsolódnak egymáshoz és zárt kört alkotnak. . A 12.2. ábrán látható téglalap alakú keret zárt hurok. Háromszor statikailag határozatlan, hiszen ahhoz, hogy statikailag meghatározhatóvá alakíthassuk, egy elemét le kell vágni és három többletkapcsolatot meg kell szüntetni. Ezen kötések reakciói a következők: a vágás helyén ható hosszirányú erő, keresztirányú erő és hajlítónyomaték; nem határozhatók meg statikus egyenletekkel. Hasonló feltételek mellett, a statikus határozatlanság értelmében, létezik bármely zárt kontúr, amely mindig háromszor statikailag határozatlan.

A csuklópánt beépítése egy olyan keretszerelvénybe, amelyben két rúd találkozik, vagy a rúd tengelyén bárhol elhelyezhető, eltávolít egy kapcsolatot, és eggyel csökkenti a statikus határozatlanság általános mértékét. Az ilyen csuklópántot egyszeresnek vagy egyszerűnek nevezik (12.3. ábra).

Általánosságban elmondható, hogy minden zsanér egy csomópontban van összekötve c rudak, csökkenti a statikus bizonytalanság mértékét c-1 , mivel egy ilyen zsanér helyettesíti c-1 egyszeres zsanérok (12.3. ábra). Így a rendszer statikus határozatlanságának mértékét zárt körvonalak jelenlétében a képlet határozza meg.

A statikusan határozatlan olyan rendszer, amelyet nem lehet pusztán statikus egyenletekkel kiszámítani, mivel szükségtelen kapcsolatai vannak. Az ilyen rendszerek kiszámításához további egyenleteket állítanak össze, amelyek figyelembe veszik a rendszer deformációit.

Statikailag határozatlan rendszerek számos jellemző tulajdonsággal rendelkezik:

1. Statikailag határozatlan szerkezetek merevebbek, mint a megfelelőek statikailag meghatározható, mivel további kapcsolataik vannak.
2. B statikailag határozatlan rendszerekhez képest kisebb a belső erő, ami meghatározza a hatékonyságukat statikailag meghatározható rendszerek azonos külső terhelés alatt.
3. Felesleges kapcsolatok feltörése statikailag határozatlan A rendszer nem mindig vezet tönkretételhez, miközben a kommunikáció megszakad statikailag meghatározható rendszer geometriailag változóvá teszi.
4. Számításhoz statikailag határozatlan rendszereket először az elemek keresztmetszeteinek geometriai jellemzőivel kell meghatározni, pl. valójában az alakjuk és a méretük, mivel változásuk a kapcsolatokban fellépő erők megváltozásához és az erők új eloszlásához vezet a rendszer minden elemében.
5. Számításkor statikailag határozatlan rendszerek esetén előre ki kell választani az építőanyagot, mivel ismerni kell annak rugalmassági modulusait.
6. B statikailag határozatlan rendszerek, hőmérsékleti hatások, támasztékok lerakódása, gyártási és szerelési pontatlanságok további erőket okoznak.

Fő számítási módszerekstatikailag határozatlan rendszerek a következők:

1. Kényszer módszer. Itt az erőfeszítéseket – erőket és pillanatokat – ismeretlennek tekintik.
2.Mozgásos módszer. Ismeretlenek a deformációs tényezők - elfordulási szögek és lineáris elmozdulások.
3.Vegyes módszer. Itt az ismeretlenek egy része az erőfeszítést, a másik része pedig az elmozdulást jelenti.
4. Kombinált módszer. Az aszimmetrikus terhelések szimmetrikus rendszereinek kiszámításakor használják. Ebből kiderül, hogy egy adott terhelés szimmetrikus összetevőjére célszerű a rendszert eltolásos módszerrel, a fordítottan szimmetrikus komponensre pedig erőmódszerrel számolni.
A különösen összetett rendszerek számításánál a fenti analitikai módszerek mellett különféle numerikus módszereket is alkalmaznak.

Az előző bekezdésben tárgyalt további egyenletek megszerzéséhez először a megadott n-szeres transzformációt kell végezni statikailag határozatlan rendszert statikusan meghatározott rendszerré alakítani, eltávolítva belőle a szükségtelen kapcsolatokat. Az így kapott statikusan definiálható rendszert ún alapvető. Vegye figyelembe, hogy egy adott rendszer statikailag meghatározhatóvá alakítása nem kötelező. Néha az erőmódszer módosítását alkalmazzák, amelyben a fő rendszer lehet statikailag határozatlan ennek a kérdésnek a bemutatása azonban túlmutat a kézikönyv keretein. Az esetleges kapcsolatok kiküszöbölése nem változtatja meg a rendszer belső erőit és deformációit, ha további erők és nyomatékok hatnak rá, amelyek a kiselejtezett kapcsolatok reakciói. Ez azt jelenti, hogy ha egy adott terhelést és a távoli kapcsolatok reakcióit alkalmazzuk a fő rendszerre, akkor a fő és az adott rendszer válik egyenértékű.

Egy adott rendszerben a meglévő merev kötések irányában nem történhetnek mozgások, ideértve azokat is, amelyek a főrendszerre való áttérés során el lettek dobva, ezért a főrendszerben a kiselejtezett kapcsolatok irányába történő mozgást kell végezni. egyenlő nullával. Ehhez pedig az eldobott kötések reakcióinak szigorúan meghatározott értékekkel kell rendelkezniük.

A nulla elmozdulás feltétele az n-ből bármely i-edik kapcsolat irányában az erőhatások függetlenségének elve alapján a következőképpen alakul:

ahol az első index a mozgás irányát és a kiselejtezett kapcsolat számát jelenti, a második pedig a mozgást okozó okot, pl. a k-edik kötés reakciója által az i-edik kötés irányába történő elmozdulás; - elmozdulás az i-edik kapcsolat irányába, amelyet a teljes külső terhelés egyidejű hatása okoz.

Az erőmódszerben a k-edik kötés reakcióját általában Xk-vel jelöljük. Figyelembe véve ezt a megjelölést és a Hooke-törvény érvényessége miatt, az elmozdulások a következőképpen ábrázolhatók:

ahol az i-edik kötés irányában a reakció által okozott egységnyi (vagy specifikus) elmozdulás, azaz. olyan reakció, amely egybeesik az Xk irányával, de egyenlő az egységgel.

Ha a (2)-t (1) behelyettesítjük, a következőt kapjuk:

Fizikai jelentés(3) egyenlet: a főrendszerben az i-edik eldobott kapcsolat irányában a mozgás nulla.

Ha a (3)-hoz hasonló kifejezéseket írunk az elvetett kapcsolatok teljes halmazára, azt kapjuk kanonikus egyenletrendszererő módszer:

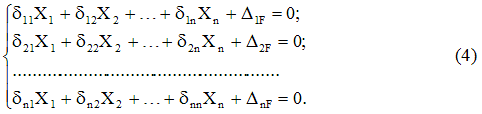
A (4) egyenlet alakja, i.e. az egyes tagok számát és teljes számát csak a rendszer statikus határozatlanságának mértéke határozza meg, és nem függ annak sajátosságaitól.

A kanonikus egyenletrendszer (4) együtthatóit a Mohr-Vereshchagin módszerrel határozzuk meg a megfelelő diagramok szorzásával. Mindezek az együtthatók, amint azt fentebb említettük, elmozdulásokat jelentenek; az ismeretlenekhez tartozó együtthatók egységeltolódások, a szabad tagok pedig azok teherszállítás. Az egységmozgások fel vannak osztva a főbbek, a főátló mentén helyezkedik el, és azonos indexekkel és oldal(). A fő mozgások mindig pozitívak, ellentétben a másodlagos mozgásokkal. A szimmetrikusan elhelyezkedő elmozdulások az elmozdulások reciprocitásáról szóló tételnek megfelelően egyenlőek egymással, azaz. .

A vizsgált tervezés jellemzőitől függetlenül a következő számítási sorrendet különböztethetjük meg statikusan határozatlan rendszerekre erő módszer:

1. Határozza meg statikus határozatlanság foka.
2. Válassza ki a fő rendszert.
3. Alkossunk egy ekvivalens rendszert.
4. Rögzítse a rendszert kanonikus egyenletek.
5. Készítse el a vizsgált szerkezet elemeiben fellépő belső erőtényezők egység- és terhelési diagramjait.
6. Számítsa ki a kanonikus egyenletrendszer ismeretlenek együtthatóit és szabad tagját!
7. Készítsen teljes egységdiagramot!
8. Végezze el az ismeretlen és szabad kifejezések együtthatóinak univerzális ellenőrzését.
9. Oldja meg a (4) rendszert, azaz. meghatározza az extra kapcsolatok reakcióit.
10. Készítsen diagramokat a kialakuló belső erőtényezőkről egy adott rendszerre (más szóval végső diagramok).
11. Végezzen statikus és kinematikai ellenőrzéseket.
Vegye figyelembe, hogy a fenti algoritmus 7., 8., 11. pontjai nem feltétlenül szükségesek, bár lehetővé teszik a számítás helyességének ellenőrzését. Az egy extra csatlakozással rendelkező rendszerek esetében pedig a 7. és 8. pont egyszerűen értelmetlen, mivel ebben az esetben a teljes egységdiagram egybeesik az egységgel.
Nézzünk meg részletesebben a fenti számítási szakaszok közül néhányat.

Ez a számítás legfontosabb szakasza, mivel a főrendszer ésszerű megválasztása jelentősen leegyszerűsíti a számítási munkát. Tekintsük a szükségtelen kapcsolatok eltávolításának lehetséges módjait, amelyek meghatározzák a fő rendszer típusát.

1. A szükségtelen csatlakozások eltávolítása egyes támasztékok teljes eltávolításával vagy kevesebb csatlakozású támasztékokkal való helyettesítésével történik. Az eldobott kötések irányába ható reakciók extra ismeretlenek. Az 1. b, c, d ábra az ezzel a módszerrel kapott ekvivalens rendszer különféle változatait mutatja a kerethez (1. ábra, a).

2. A csuklópántok elhelyezése a rudak közbenső szakaszaiban lehetővé teszi az egyes ilyen szakaszokon a hajlítónyomatéknak megfelelő kapcsolat kialakítását. Ezek a pillanatok szükségtelen ismeretlenek. Az n=3 statikus határozatlansági fokú kerethez (2. ábra, a) a főrendszer kiválasztásakor három zsanér beépítése szükséges. Ezeknek a csuklópántoknak a helyzete tetszőleges lehet, de kielégíti a rendszer geometriai változhatatlanságának követelményét (2.b ábra).

3. A rúd elvágása megszünteti az M, Q, N belső erőknek megfelelő három csatlakozást (2. ábra, c). Egyes esetekben (2. ábra, d) egy rúd csuklópánt mentén történő elvágása két csatlakozást szabadít fel (2. ábra, e), és egy egyenes rúd vágásakor csuklópántokkal a végén egy csatlakozás szabadul fel (2. ábra, f).

A statikailag határozatlan rendszer összefüggései között különbséget tesznek a feltétlenül szükséges és a feltételesen szükséges között. A feltétlenül szükséges kapcsolatok közé tartoznak azok a kapcsolatok, amelyek eltávolítása esetén a rendszer geometriailag változtathatóvá válik. Egy feltétlenül szükséges összefüggést a benne lévő erőfeszítés statikus meghatározhatósága jellemez, azaz. egy ilyen kötés reakciója az egyensúlyi feltételből számítható ki. A fő rendszer kiválasztásakor a feltétlenül szükséges csatlakozásokat nem lehet elvetni.

A kapcsolatokat, ha eltávolítják, a rendszer geometriailag továbbra is változatlan marad, feltételesen szükségesnek nevezzük. Az a rendszer, amelyről az ilyen kapcsolatot eltávolították, lehet az elsődleges rendszer erő módszer.

A számítás ezen szakaszát a belső erőtényezők egység- és terhelési diagramjainak felépítése előzi meg (gerendákhoz és keretekhez - a hajlítónyomatékok diagramjai). Az egységdiagramok egy dimenzió nélküli egységerő vagy egy dimenzió nélküli egységnyomaték hatásából épülnek fel, amelyek irányában egybeesnek az ekvivalens rendszerben a megfelelő extra ismeretlen irányával, és jelölésükkel, az egységdiagramot pedig -vel jelöljük.

A terhelési diagram a fő rendszerre gyakorolt külső terhelésből készült. Ebben az esetben az összes külső terhelés egyidejű hatásából egy diagramot vagy több diagramot készíthet, külön az egyes alkalmazott terhelésektől. Egy terhelési diagram ilyen felosztása több egyszerűbbre általában csak akkor tanácsos, ha a ható terhelések között egyenletesen eloszlik, és az alatta lévő megfelelő szakaszban a nyomatékok diagramja váltakozik előjelben. Ebben az esetben minden kanonikus egyenletben a szabad tagok száma megegyezik a megszerkesztett terhelési diagramok számával.

Az egység- és terheléselmozdulások (a kanonikus egyenletek együtthatói és szabadtagjai) általános esetben Mohr-módszerrel számíthatók ki. Gerendák és keretek esetében ezt Verescsagin szabályával lehet megtenni.

1,42 NM + 1,73 NM = 45

3,15 NM = 45,

14,3 kN tehát

NST = 1,42 14,3 = 20,3 kN.

Az univerzális ellenőrzés elvégzéséhez össze kell állítani egy teljes egységdiagramot - a fő rendszerre alkalmazott összes egységerő egyidejű hatásából származó pillanatok diagramját:

Szorozzuk meg a teljes egységdiagramot a diagrammal:

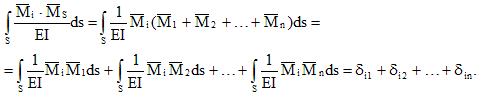
Így a teljes és az i-edik egységdiagram szorzásának eredménye az i-edik kapcsolat irányába történő elmozdulás az egyes extra ismeretlenek együttes hatásából. Ez az eltolás egyenlő az i-edik kanonikus egyenlet együtthatóinak összegével:

Ezt a csekket hívják Vonalról vonalraés minden kanonikus egyenletre teljesül.
n soronkénti ellenőrzés helyett leggyakrabban egyet hajtanak végre - univerzális ellenőrzés, amely abból áll, hogy a teljes egységdiagramot megszorozzuk önmagával és ellenőrizzük a feltételt:

Ha az univerzális ellenőrzést végrehajtják, akkor az egység mozgásait helyesen számítják ki; ha nem, akkor soronkénti ellenőrzéseket kell végezni, amelyek lehetővé teszik annak tisztázását, hogy a számítás során melyik elmozdulás hibázott.

A rakomány mozgásának ellenőrzéséhez meg kell szorozni a hajlítónyomatékok teljes mértékegységét és terhelési diagramjait:

Így a (4) kanonikus egyenletrendszer szabad tagjainak ellenőrzése a feltétel teljesüléséből áll.