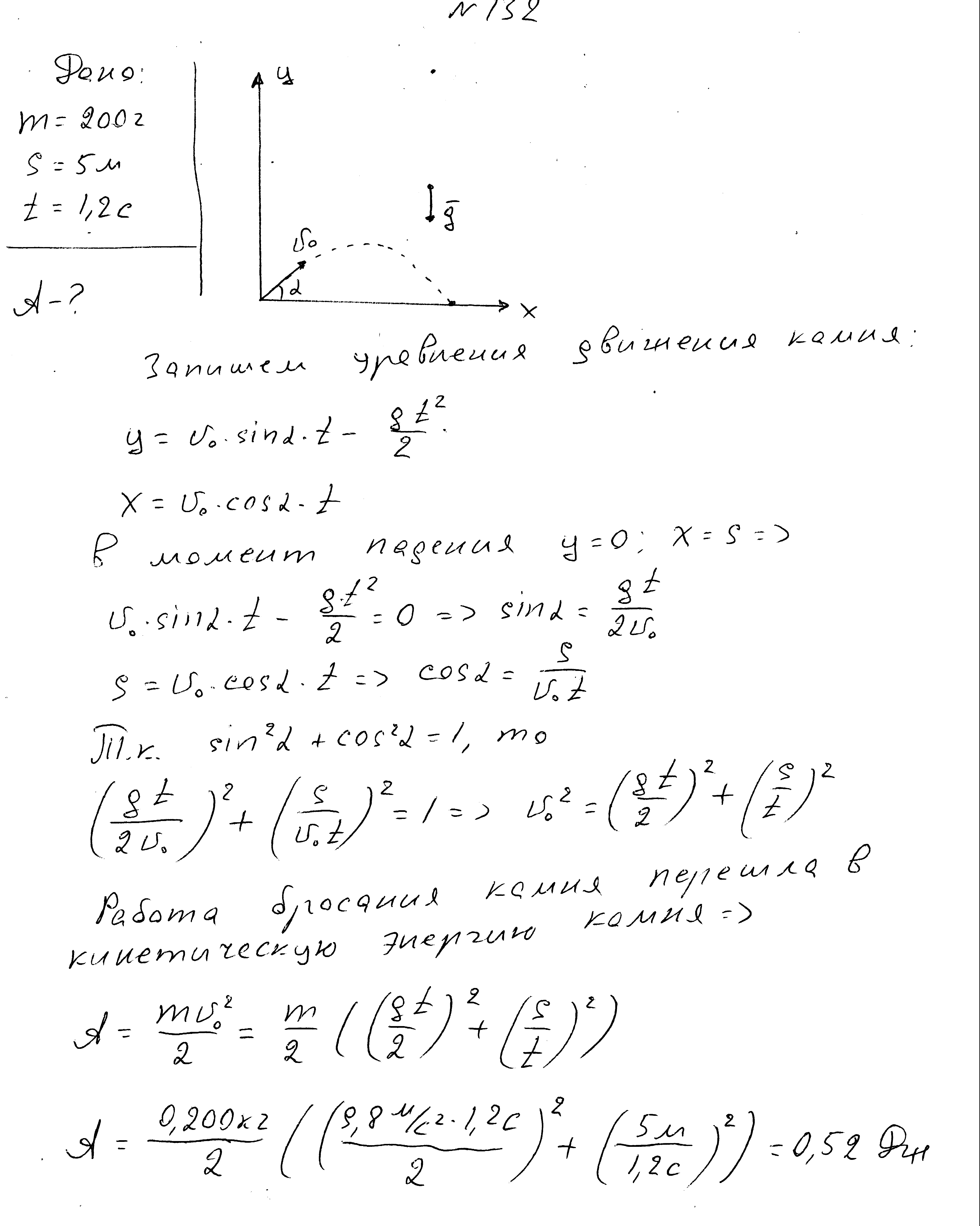A vízszintessel szögben bedobott test mozgásának tanulmányozása. A vízszinteshez képest szögben bedobott test mozgása! Fizika: a vízszintessel szöget bezárt test mozgása

Ha egy testet a horizonthoz képest szögben dobnak, akkor repülés közben a gravitációs erő és a légellenállás ereje hat rá. Ha az ellenállási erőt figyelmen kívül hagyjuk, akkor az egyetlen erő marad a gravitáció. Ezért Newton 2. törvényének köszönhetően a test a gravitáció gyorsulásával egyenlő gyorsulással mozog; gyorsulás vetületei a koordináta tengelyekre ax = 0, ay = - g.

1. ábra A vízszintessel szögben bedobott test kinematikai jellemzői

Egy anyagi pont bármely összetett mozgása a koordinátatengelyek mentén független mozgások szuperpozíciójaként ábrázolható, és a különböző tengelyek irányában a mozgás típusa eltérő lehet. Esetünkben egy repülő test mozgása két független mozgás szuperpozíciójaként ábrázolható: a vízszintes tengely mentén egyenletes mozgás (X-tengely) és egyenletesen gyorsított mozgás a függőleges tengely mentén (Y-tengely) (1. ábra). .

A test sebesség-előrejelzései ezért az idő múlásával a következőképpen változnak:

ahol $v_0$ a kezdeti sebesség, $(\mathbf \alpha )$ a dobási szög.

Az origó választásunkkal a kezdeti koordináták (1. ábra) $x_0=y_0=0$. Akkor kapjuk:

(1)

Elemezzük az (1) képleteket. Határozzuk meg a kidobott test mozgási idejét. Ehhez állítsuk az y koordinátát nullára, mert a leszállás pillanatában a test magassága nulla. Innen kapjuk a repülési időt:

A második időérték, amelynél a magasság nulla, nulla, ami megfelel a dobás pillanatának, azaz. ennek az értéknek fizikai jelentése is van.

A repülési távolságot az (1) első képletből kapjuk. A repülési távolság az x koordináta értéke a repülés végén, azaz. $t_0$ időpontban. Ha az (1) első képletbe behelyettesítjük a (2) értéket, a következőt kapjuk:

Ebből a képletből látható, hogy a legnagyobb repülési távolságot 45 fokos dobási szög mellett érjük el.

A dobott test maximális emelési magasságát a második képletből (1) kaphatjuk meg. Ehhez a képletbe a repülési idő felével egyenlő időértéket kell behelyettesíteni (2), mert A repülési magasság a pálya felezőpontján van a legnagyobb. Számításokat végezve azt kapjuk

Az (1) egyenletekből megkaphatjuk a test röppályájának egyenletét, azaz. egy egyenlet, amely a test x és y koordinátáit rögzíti mozgás közben. Ehhez ki kell fejeznie az időt az első egyenletből (1):

és behelyettesítjük a második egyenletbe. Akkor kapjuk:

Ez az egyenlet a mozgási pálya egyenlete. Látható, hogy ez egy parabola egyenlete lefelé ágakkal, amint azt a másodfokú tag előtti „-” jel jelzi. Figyelembe kell venni, hogy a $\alpha $ dobási szög és függvényei itt egyszerűen állandók, azaz. állandó számok.

Egy testet v0 sebességgel $(\mathbf \alpha )$ szögben dobnak a horizonthoz. Repülési idő $t = 2 s$. Hmax mekkora magasságra emelkedik a test?

$$t_B = 2 s$$ $$H_max - ?$$

A test mozgásának törvénye a következőképpen alakul:

$$\left\( \begin(array)(c) x=v_(0x)t \\ y=v_(0y)t-\frac(gt^2)(2) \end(array) \right.$ $

A kezdeti sebességvektor $(\mathbf \alpha )$ szöget zár be az OX tengellyel. Ennélfogva,

\ \ \

Egy követ dobnak a hegy tetejéről = 30$()^\circ$ szögben a horizonthoz $v_0 = 6 m/s$ kezdeti sebességgel. Ferde síkszög = 30$()^\circ$. Milyen messze fog leszállni a kő a dobási ponttól?

$$ \alpha =30()^\circ$$ $$v_0=6\ m/s$$ $$S - ?$$

Helyezzük a koordináták origóját a dobási pontba, OX - a ferde sík mentén lefelé, OY - merőlegesen a ferde síkra felfelé. A mozgás kinematikai jellemzői:

A mozgás törvénye:

$$\left\( \begin(array)(c) x=v_0t(cos 2\alpha +g\frac(t^2)(2)(sin \alpha \ )\ ) \\ y=v_0t(sin 2 \alpha \ )-\frac(gt^2)(2)(cos \alpha \ ) \end(array) \right.$$ \

A kapott $t_В$ értéket behelyettesítve $S$-t kapunk:

3 másodperc volt hátra az 1972-es müncheni olimpia kosárlabdatornája zárómérkőzéséig. Az amerikaiak – az amerikai csapat – már győzelmüket ünnepelték! Csapatunk - a Szovjetunió válogatottja - mintegy 10 ponttal nyert a nagy álomcsapat ellen...

Pár perccel a meccs vége előtt. De miután minden előnyét elveszítette, már egy pontot veszített 49:50 arányban. Aztán megtörtént a hihetetlen! Ivan Edeshko a végvonal mögül dobja a labdát az egész pályán az amerikai gyűrű alatt, ahol Alekszandr Belov centerünk fogadja a labdát két ellenféltől megkörnyékezve, és kosárba teszi. 51:50 – Olimpiai bajnokok vagyunk!!!

Gyerekként a legerősebb érzelmeket éltem át – először csalódást és haragot, majd őrült örömöt! Ennek az epizódnak az érzelmi emléke életem végéig bevésődött a tudatomba! Nézze meg a videót az interneten „Alexander Belov aranydobása” kérésre, nem fogja megbánni.

Az amerikaiak ezután nem ismerték el a vereséget, és nem voltak hajlandók ezüstérmet kapni. Meg lehet csinálni három másodperc alatt, amit a játékosaink? Emlékezzünk a fizikára!

Ebben a cikkben megvizsgáljuk a horizonthoz képest szögben elvetett test mozgását, készítünk Excelben egy programot a probléma megoldására a bemeneti adatok különféle kombinációival, és megpróbálunk válaszolni a fent feltett kérdésre.

Ez egy meglehetősen jól ismert probléma a fizikában. Esetünkben a vízszinteshez képest szögben bedobott test egy kosárlabda. Kiszámoljuk egy Ivan Edeshko által az egész pályán átdobott és Alekszandr Belov kezébe kerülő labda kezdeti sebességét, idejét és röppályáját.

A kosárlabda repülés matematikája és fizikája.

Az alábbiakban bemutatott képletek és számításokexcel univerzálisak a horizonthoz képest szögben elvetett testekkel kapcsolatos problémák széles köréhez, amelyek parabola pályán repülnek, anélkül, hogy figyelembe vennék a légsúrlódás hatását.

A számítási diagram az alábbi ábrán látható. Indítsa el az MS Excelt vagy az OOo Calc programot.

Kiinduló adatok:

1. Mivel a Föld bolygón vagyunk, és egy ballisztikai problémát fontolgatunk - a testek mozgását a Föld gravitációs mezőjében, ezért először is felírjuk a gravitációs tér fő jellemzőjét - a szabadesés gyorsulását. g m/s 2-ben

D3 cellába: 9,81

2. A kosárlabdapálya méretei: 28 méter hosszú és 15 méter széles. A labda vízszintes távolsága szinte a teljes pályától a gyűrűig az ellenkező alapvonaltól xírd méterben

D4 cellába: 27,000

3. Ha feltételezzük, hogy Edeshko körülbelül két méteres magasságból dobta be, és Belov éppen valahol a karika magasságában fogta el a labdát, akkor 3,05 méteres kosárlabdakarikával a kiindulási és érkezési pontok közötti függőleges távolság. a labda 1 méteres lesz. Írjuk fel a függőleges elmozdulást y méterben

a D5 cellához: 1,000

4. A videófelvételen mért méréseim szerint a labda kilövési szöge α 0 Edeshko kezétől nem haladta meg a 20°-ot. Írjuk be ezt az értéket

a D6 cellához: 20,000

Számítási eredmények:

Alapvető egyenletek, amelyek leírják a horizonttal szögben bedobott test mozgását a légellenállás figyelembevétele nélkül:

x =v 0*kötözősaláta α 0 *t

y =v 0*bűn α 0 *t -g *t 2 /2

5. Kifejezzük az időt t az első egyenletből helyettesítse be a másodikba, és számítsa ki a labda kezdeti sebességét v 0 m/s-ban

a D8 cellában: =(D3*D4^2/2/COS (RADIANS(D6))^2/(D4*TAN (RADIANS(D6)) -D5))^0,5 =21,418

v 0 =(g *x 2 /(2*(cosα 0 ) 2 *(x *tgα 0 -y )) 0,5

6. Labdarepülési idő Edeshko kezéből Belov kezébe t Számoljunk másodpercekben, most tudva v 0 , az első egyenletből

a D9 cellában: =D4/D8/COS (RADIÁNOK(D6)) =1,342

t = x /(v 0 * kötözősalátaα 0 )

7. Határozzuk meg a labda repülési sebességének irányszögét α én a számunkra érdekes pályaponton. Ehhez írjuk fel a kezdeti egyenletpárt a következő formában:

y =x *tgα 0 -g *x 2 /(2*v 0 2*(kötözősalátaα 0 ) 2)

Ez a parabola egyenlete - egy repülési útvonal.

Meg kell találnunk a számunkra érdekes pontban a parabola érintőjének dőlésszögét - ez lesz a szög α én. Ehhez vegye a deriváltot, amely az érintőszög érintője:

y' =tgα 0 -g *x /(v 0 2*(kötözősalátaα 0 ) 2)

Számítsuk ki a labda Belov kezébe érkezési szögét α én fokokban

a D10 cellában: =ATAN (TAN (RADIANS(D6)) -D3*D4/D8^2/COS (RADIANS(D6))^2)/PI()*180 =-16,167

α én = arctgy ’ = arctg(tgα 0 — g * x /(v 0 2 *(kötözősalátaα 0 ) 2))

A számítás Excelben lényegében kész.

Egyéb fizetési lehetőségek:

Az írott program segítségével gyorsan és egyszerűen végezhet számításokat a kezdeti adatok más kombinációival.

Legyen adott vízszintes x = 27 méter , függőleges y = 1 méteres repülési távolság és kezdeti sebesség v 0 = 25 m/s.

Meg kell találnunk a repülési időt tés indulási szögek α 0 és érkezés α én

Használjuk az MS Excel „Parameter Selection” szolgáltatását. Több blogcikkben többször is részletesen elmagyaráztam, hogyan kell használni. A szolgáltatás használatáról bővebben olvashat.

A D8 cellában lévő értéket 25 000-re állítjuk úgy, hogy a D6 cellában lévő értéket megváltoztatjuk annak kiválasztásával. Az eredmény az alábbi képen látható.

A számítás ezen változatában az Excelben (ahogy az előzőben is) a forrásadatok kék kerettel, az eredmények pedig piros téglalap alakú keretekkel vannak kiemelve!

Beállítás a táblázatbanExcel valamilyen érdekes érték az egyik halványsárga kitöltésű cellában, ha az egyik világos türkiz kitöltésű cellában egy megváltozott értéket választ ki, általában tíz különböző lehetőséget kaphat a rádobott test mozgásának problémájának megoldására. szög a horizonthoz tíz különböző halmaz eredeti adatához!!!

Válasz a kérdésre:

Válaszoljunk a cikk elején feltett kérdésre. Ivan Edeshko által küldött labda számításaink szerint 1,342 másodperc alatt repült Belovhoz. Alekszandr Belov elkapta a labdát, landolt, ugrott és dobott. Rengeteg ideje volt minderre - 1,658 másodperc! Ez valóban elegendő szabadidő! A videófelvételek részletes áttekintése megerősíti a fentieket. Játékosainknak három másodpercük volt arra, hogy a végvonalukról az ellenfél palánkjára szállítsák a labdát és bedobják a karikába, így nevüket arannyal írták be a kosárlabda történetébe!

Könyörgöm tiszteletteljes szerző munkája fájl letöltése előfizetés után cikkhirdetésekre!

Szabadesés az egyenletesen gyorsított mozgás speciális esetét képviseli kezdeti sebesség nélkül. Ennek a mozgásnak a gyorsulása megegyezik a gravitáció gyorsulásával, amelyet gravitációs gyorsulásnak is neveznek. Erre a mozgásra a következő képletek érvényesek:

u t
g
h- a magasság, ahonnan a test leesik
t- az idő, amely alatt az esés folytatódott

Jegyzet:

• A légellenállást ezekben a képletekben nem veszik figyelembe.
• A gravitációs gyorsulás adott értékű (9,81 (m/s?)) a földfelszín közelében. A g értéke a Föld felszínétől más távolságban is változik!

Függőlegesen felfelé dobott test mozgása

A függőlegesen felfelé dobott test egyenletesen lassan, kezdeti sebességgel mozog u0és a gyorsulás a = -g. A test időbeli mozgása t az emelési magasságot jelenti h.E mozgásra a következő képletek érvényesek:

U0- a test mozgásának kezdeti sebessége
U- az a sebesség, amellyel a test idővel leesik t
g- szabadesési gyorsulás, 9,81 (m/s?)
h- az a magasság, amelyre a test idővel fel fog emelkedni t
t- idő

A test sebessége egy bizonyos magasságban:

Maximális emelési magasság:

A maximális magasságra való felemelkedés ideje:

Egymáshoz képest szögben irányított mozgások összeadása.

A test egyszerre több transzlációs mozgásban is részt vehet. Mivel a gyorsulás, a sebesség és az elmozdulás vektormennyiségek, a vektoros (geometriai) összeadás törvényei szerint összeadhatók. Azok. paralelogramma szabály szerint.

Bármely mozgási karakterisztika eredő értéke kiszámítható.

Ha:
Fel- a kapott pillanatnyi sebesség,
U1- az első mozgás pillanatnyi sebessége,
U2- a második mozgás pillanatnyi sebessége,
? - a sebességvektorok által alkotott szög u1És u2,
Ekkor a koszinusz tételt használva a következőt kapjuk:

Ha az 1. és 2. mozgás derékszögben történik egymásra, akkor a képlet leegyszerűsíti, mert

Vízszintesen eldobott test mozgása.

A vízszintesen dobott test mozgása két egymásra merőleges mozgás kombinációja:
- vízszintes (egyenletes) mozgás,
- függőleges (szabadesés)

Vízszintesen elhajított test röppályájának egyenlete

Ha egy vízszintesen dobott test pályáját megszerkesztjük a koordinátarendszerben xy, a dobási pontot figyelembe véve a koordináták origójának, és az ordináta tengelyének irányát egybeesik a szabadesés gyorsulási vektor irányával, akkor a pálya egyes pontjainak koordinátái a test vízszintes irányú mozgását jelentik (állandó sebességű mozgás U0) és függőleges irányban (egyenletesen gyorsított mozgás gyorsulással g)

x, y- test koordinátái,
u0
g
t- utazási idő(k)

Vízszintesen elhajított test röppályájának egyenlete alábbiak szerint:

gés a test kezdeti sebessége u0állandó mennyiségek, akkor a koordináta y négyzetével arányos x, azaz a mozgás pályája egy parabola, amelynek csúcsa a mozgás kezdőpontjában van.

Vízszintesen dobott test vektorpozíciója, képlet

A vízszintesen dobott test pályájának minden pontjának helyzete a helyzetvektorral adható meg r, amely a kapott elmozdulást jelenti:

vagy Pozícióvektor:

x-koordináta:

Y-koordináta:

Megjegyzés: A képletek nem veszik figyelembe a légellenállást.

A vízszintessel szöget zárt test mozgásegyenlete.

A pályapont koordinátáit a következő egyenletek írják le:

x, y- a test koordinátái
U0- kezdeti testsebesség (m/s)
? - az a szög, amelynél a test a horizonthoz viszonyul (°)
g- szabadesési gyorsulás 9,81 (m/s2)
t- utazási idő(k)

A képletekből a t paraméteren keresztül levezetjük az általánost a vízszintessel szöget zárt test mozgásegyenlete

A gravitáció gyorsulása óta g, ? - a test horizonthoz viszonyított szöge és a test kezdeti sebessége u0állandó mennyiségek, akkor a koordináta y négyzetével arányos x, azaz a mozgás pályája egy parabola, a kiindulási pont az egyik ágán van, a parabola csúcsa pedig a test maximális magassági pontja.

A horizonttal szögben eldobott test maximális magasságáig való felemelkedésének ideje.

A maximális magasságra való felemelkedés idejét abból a feltételből határozzuk meg, hogy a pillanatnyi sebesség függőleges összetevője nulla

ebből az egyenletből a következőket kapjuk:

U0- a test kezdeti sebessége (m/s),
?
g- szabadesési gyorsulás 9,81 (m/s2),
thmax- a maximális magasságra való felemelkedés ideje (s)

A vízszintessel szögben elhajított test dobási távolsága.

Dobási tartomány vagy rombolási sugár a teljes mozgási idő képletei és a testkoordináták képlete határozzák meg

helyettesítő tsmax a kifejezésbe és leegyszerűsítve a következőket kapjuk:

U0- a test kezdeti sebessége (m/s),
? - az a szög, amelyben a test a horizonthoz képest el van vetve (°),
g- szabadesési gyorsulás 9,81 (m/s2),
tsmax- teljes utazási idő (s)

A vízszinteshez képest szögben bedobott test mozgása

Tekintsük a V 0 sebességgel dobott test mozgását, amelynek vektora a horizonttal α szöget zár be, az XOY síkban, a testet a dobás pillanatában a koordináták origójába helyezve, amint az ábra mutatja. az 1. ábrán.

Ellenállási erők hiányában a horizonthoz képest szögben bedobott test mozgása a gravitáció hatására a görbe vonalú mozgás speciális esetének tekinthető. Newton 2. törvényének alkalmazása

Az 1. ábra felfelé néz, abban az esetben, ha az OY tengely lefelé irányul, akkor a vektor vetülete

2 a műveleti erősítő tengelyén pozitív lesz(a problémák feltételeit elolvasva, saját maga válassza ki a tengelyek irányát, ha ez a feltételek között nincs feltüntetve).

Az a gyorsulásvektor vetületeinek értékei az OX és az OU tengelyeken okot adnak arra, hogy

a következő kimenet:

∙ a vízszintessel szögben bedobott test egyidejűleg két mozgásban vesz részt - vízszintesen egyenletesen és mentén egyenletesen változó

Egyenletesen változó mozgás esetén a sebesség és az elmozdulás időfüggőségét a következő egyenletek adják meg:

a test koordinátái a t időpontban.

A t mozgása során (a dobás pillanatától a ráesés pillanatáig

szint) a test felemelkedik egy maximális hmax magasságra, leereszkedik róla és L távolságra (repülési távolság) elrepül a dobási ponttól - lásd az 1. ábrát.

1) Testmozgási idő t megtalálható a Sy in testkoordináták értékeinek figyelembevételével

Voy és (14) értékét behelyettesítve a (13) rendszer második egyenletébe, megkapjuk

2) Repülési tartomány L megtalálható, figyelembe véve a test koordinátáit Sх in

kezdeti időpillanat és t időpont (lásd 1. ábra)

Vox és (17) értékét behelyettesítve a (13) rendszer első egyenletébe, megkapjuk

3) Maximális emelési magasság h max érték alapján megtalálható

V testsebesség a test maximális emelési pontjában

A (16) és (22) értékek összehasonlítása alapot ad a következtetésre

· mozgás ideje a maximális testemelés magasságáig (t alatt ) egyenlő a test leereszkedésének idejével (tп) erről a magasságról, és egyenlő a test teljes mozgásának idejének felével, a dobás pillanatától az azonos szintre zuhanás pillanatáig

A V 0 sebességgel dobott test mozgásának tanulmányozása, amelynek vektora a vízszinteshez képest α szöget zár be, az XOY síkban nagyon jól látható számítógépes modellen.

"Testek szabadesése" az "Open Physics" számítógépes modellek gyűjteményében

PHYSIKON cég. Ebben a modellben különböző kezdeti feltételeket állíthat be.

Például az általunk vizsgált esetet meg kell adni (a „Clear” parancs) a kezdeti h = 0 feltétellel, és kiválasztani a V0 és α értékeket. A "Start" parancs bemutatja a test mozgását, és képet ad a mozgás pályájáról és a test sebességvektorainak irányáról meghatározott időpillanatokban.

2. ábra. A "Testek szabad esése" című számítógépmodell párbeszédablakja a részben

"Mechanika"; egy test elmozdul az origótól és ugyanarra a szintre esik.

Ha a probléma feltétele eltér az általunk vizsgált esettől, akkor szükséges

a probléma megoldásához a tengelyek irányát választva helyezze el a testet a kezdeti pillanatban

idő, ábrázolja a test pályáját az esésig, így

a test koordinátáinak meghatározásával az idő kezdeti és végső pillanatában. Akkor

használja a (3), (5), (8) és (9) egyenleteket a megoldás alapjául, és a fent tárgyalt

algoritmus a probléma megoldására.

Nézzünk speciális eseteket.

6 1. A testet nagy sebességgel dobták ki V 0 , amelynek vektora szögben van irányítvaα to

horizonton, h magasságból és a dobás pontjától L távolságra esett. y kezdőbetűre

és a fennmaradó koordináták értékei ugyanúgy lesznek kiválasztva, mint mi.

3. ábra. A "Testek szabad esése" című számítógépmodell párbeszédablakja a részben

"Mechanika"; a test h = 50m pontból elmozdul és nulla szintre esik.

2. Egy testet V 0 sebességgel vízszintesen dobtak h magasságból, és a dobás pontjától L távolságra esett. Az általunk vizsgált esethez képest az a különbség, hogy a test értékei S-t koordinálnak y a kezdeti pillanatban szintén a (25) egyenlet határozza meg,

és a fennmaradó koordináták értékei ugyanúgy lesznek kiválasztva, mint mi. De ebben az esetben a test kezdeti sebessége az OU tengelyre vetítve nullával egyenlő (mivel α = 0), azaz.

a kezdeti sebességvektor vetületei az OX és OU tengelyekre egyenlők

4. ábra. A "Testek szabad esése" című számítógépmodell párbeszédablakja a részben

"Mechanika"; egy vízszintesen eldobott test h = 50m pontból elmozdul és nulla szintre esik.

Az alábbiakban a problémák feltételeit és a szkennelt megoldásokat ismertetjük. Ha meg kell oldania egy problémát ebben a témában, itt találhat egy hasonló feltételt, és analógia útján oldja meg a sajátját. Az oldal betöltése eltarthat egy ideig a képek nagy száma miatt. Ha problémamegoldásra vagy online segítségre van szüksége fizikában, keressen minket, szívesen segítünk.

E problémák megoldásának elve az, hogy egy szabadon eső test sebességét két komponensre - vízszintesre és függőlegesre - bontják. A sebesség vízszintes összetevője állandó, a függőleges mozgás a szabadesés g=9,8 m/s 2 gyorsulásával történik. Alkalmazható a mechanikai energia megmaradásának törvénye is, amely szerint a test potenciális és mozgási energiájának összege ebben az esetben állandó.

Egy anyagi pontot 15 m/s kezdeti sebességgel a horizonthoz képest szögben dobnak. A kezdeti kinetikus energia 3-szor nagyobb, mint a pálya felső pontjában lévő pont kinetikus energiája. Milyen magasra emelkedett a pont?

Egy testet a vízszinteshez képest 40 fokos szögben dobnak 10 m/s kezdeti sebességgel. Határozza meg a távolságot, amelyet a test repül a zuhanás előtt, az emelkedés magasságát a pálya felső pontjában és a repülési időt.

Egy testet vetünk le a H magasságú toronyból, a vízszinteshez képest α szögben, v kezdősebességgel. Keresse meg a távolságot a torony és a hely között, ahol a test leesett.

Egy 0,5 kg tömegű testet a Föld felszínéről a vízszinteshez képest 30 fokos szögben, 10 m/s kezdeti sebességgel dobnak ki. Határozza meg a test potenciális és kinetikus energiáit 0,4 s után!

Egy anyagi pontot a Föld felszínéről a horizonthoz képest szögben felfelé dobnak 10 m/s kezdeti sebességgel. Határozzuk meg egy 3 m magasságban lévő pont sebességét!

Egy testet 60 fokos szögben felfelé dobnak a Föld felszínéről 10 m/s kezdeti sebességgel. Határozza meg az ütközési pont távolságát, a test sebességét az ütközési pontban és a repülési időt.

Egy testet a vízszinteshez képest szögben felfelé dobnak 20 m/s kezdeti sebességgel. Az esési pont távolsága a maximális emelési magasság 4-szerese. Keresse meg azt a szöget, amelybe a testet bedobják.

Egy testet 5 m magasságból a vízszinteshez képest 30 fokos szögben dobnak ki 22 m/s kezdeti sebességgel. Határozza meg a test repülési hatótávolságát és a test repülési idejét!

Egy testet 30 m/s kezdeti sebességgel dobnak ki a Föld felszínéről a horizonthoz képest szögben. Határozza meg a test tangenciális és normál gyorsulását a dobás utáni 1 másodperccel!

A Zesli felszínéről a vízszinteshez képest 30 fokos szögben egy testet dobnak ki 14,7 m/s kezdeti sebességgel. Határozza meg a test tangenciális és normál gyorsulását 1,25 másodperccel a dobás után!

Egy testet a vízszinteshez képest 60 fokos szögben dobnak 20 m/s kezdeti sebességgel. Mennyi idő múlva lesz a sebesség és a horizont szöge 45 fok?

Dobott labda az edzőteremben a horizonthoz képest szögben,20 m/s kezdeti sebességgel a pálya felső pontján 8 m magasságban a mennyezetet érintette és a dobás helyétől bizonyos távolságra leesett. Határozza meg ezt a távolságot és azt a szöget, amelyen a test el van vetve.

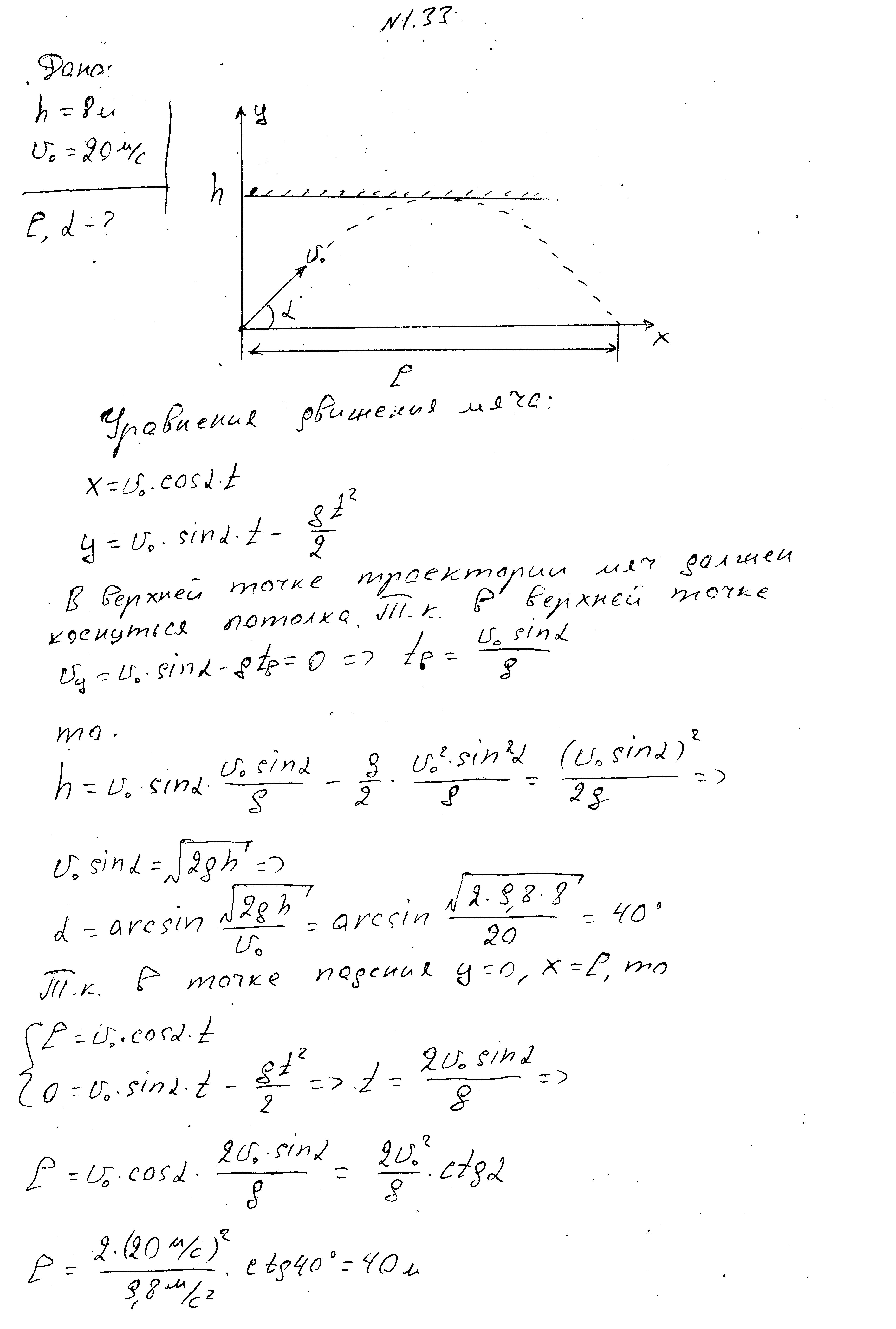
A Föld felszínéről a horizonthoz képest szögben kidobott test 2,2 s után leesett. Keresse meg a test maximális emelési magasságát.

Egy követ a vízszinteshez képest 30 fokos szögben dobnak. A kő kétszer is elért egy bizonyos magasságot – 1 és 3 másodperccel az eldobás után. Határozza meg ezt a magasságot és a kő kezdeti sebességét.

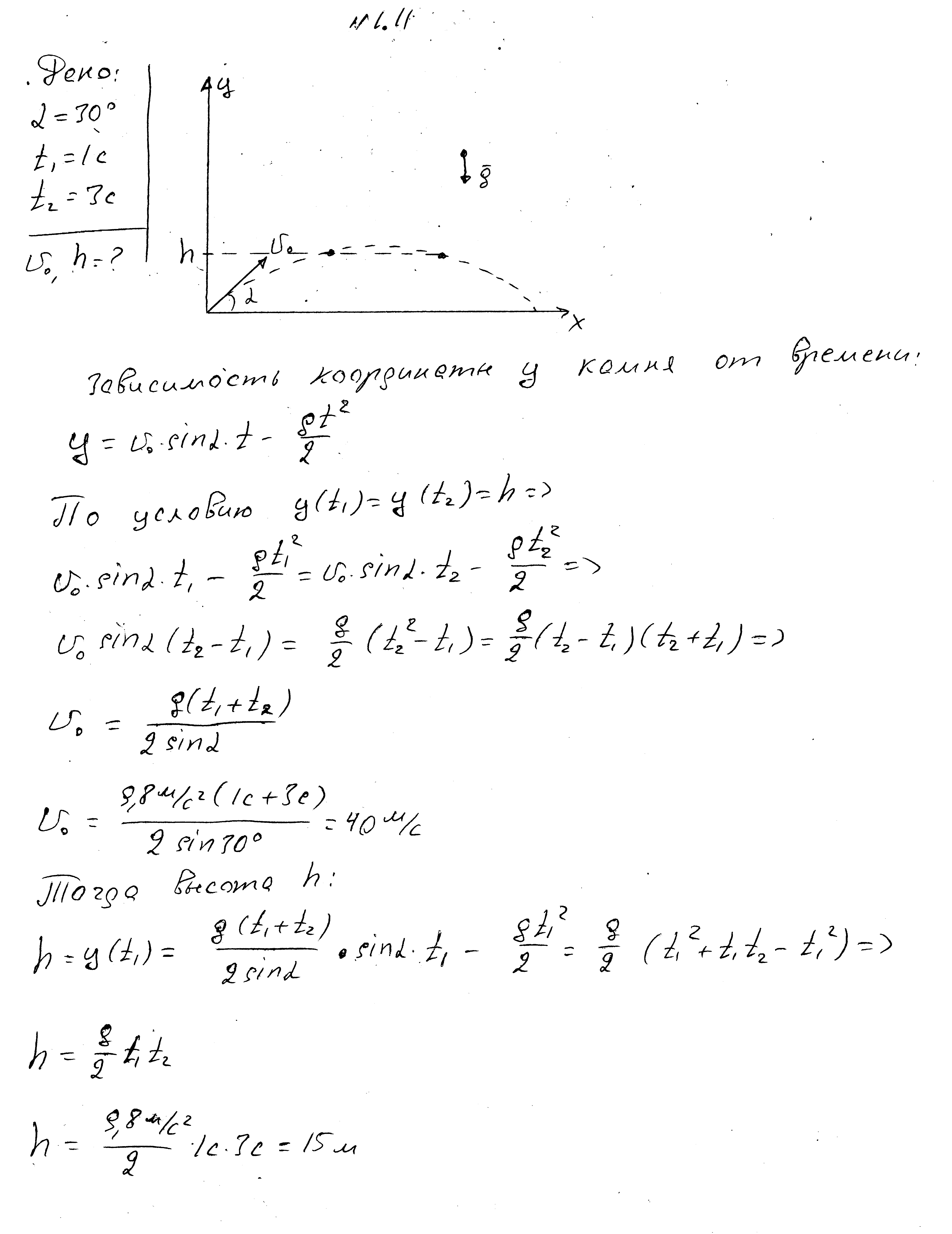
Egy követ a vízszinteshez képest 30 fokos szögben dobnak 10 m/s kezdeti sebességgel. Határozza meg a dobási pont és a kő távolságát 4 s után.

A lövedéket abban a pillanatban sütötték ki, amikor a gép a látóhatárhoz képest szögben 500 m/s kezdeti sebességgel átrepül a fegyver fölött. A lövedék 10 másodperccel a kilövés után 3,5 km-es magasságban érte a gépet. Mekkora a repülőgép sebessége?

A Föld felszínéről a vízszinteshez képest 60 fokos szögben egy 5 kg súlyú ágyúgolyót dobnak ki. A tömeg felgyorsítására fordított energia 500 J. Határozza meg a repülési távolságot és a repülési időt.

Egy testet 100 m magasságból a vízszinteshez képest 30 fokos szögben 5 m/s kezdeti sebességgel dobnak le. Keresse meg a test repülési tartományát.

Egy 200 g tömegű, a Föld felszínéről a horizonthoz képest szögben kidobott test 1,2 másodperc múlva 5 m távolságra esett. Keress egy testdobó munkát.