Чем неопределенный интеграл отличается от определенного. Определённый интеграл с переменным верхним пределом

Решение интегралов - задача легкая, но только для избранных. Эта статья для тех, кто хочет научиться понимать интегралы, но не знает о них ничего или почти ничего. Интеграл... Зачем он нужен? Как его вычислять? Что такое определенный и неопределенный интегралы? Если единственное известное вам применение интеграла – доставать крючком в форме значка интеграла что-то полезное из труднодоступных мест, тогда добро пожаловать! Узнайте, как решать интегралы и почему без этого никак нельзя обойтись.

Изучаем понятие "интеграл"

Интегрирование было известно еще в Древнем Египте. Конечно, не в современном виде, но все же. С тех пор математики написали очень много книг по этой теме. Особенно отличились Ньютон и Лейбниц , но суть вещей не изменилась. Как понять интегралы с нуля? Никак! Для понимания этой темы все равно понадобятся базовые знания основ математического анализа. Сведения о , необходимые и для понимания интегралов, уже есть у нас в блоге.

Неопределенный интеграл

Пусть у нас есть какая-то функция f(x) .

Неопределенным интегралом функции f(x) называется такая функция F(x) , производная которой равна функции f(x) .

Другими словами интеграл – это производная наоборот или первообразная. Кстати, о том, как читайте в нашей статье.

Первообразная существует для всех непрерывных функций. Также к первообразной часто прибавляют знак константы, так как производные функций, различающихся на константу, совпадают. Процесс нахождения интеграла называется интегрированием.

Простой пример:

Чтобы постоянно не высчитывать первообразные элементарных функций, их удобно свести в таблицу и пользоваться уже готовыми значениями:

Определенный интеграл

Имея дело с понятием интеграла, мы имеем дело с бесконечно малыми величинами. Интеграл поможет вычислить площадь фигуры, массу неоднородного тела, пройденный при неравномерном движении путь и многое другое. Следует помнить, что интеграл – это сумма бесконечно большого количества бесконечно малых слагаемых.

В качестве примера представим себе график какой-нибудь функции. Как найти площадь фигуры, ограниченной графиком функции?

С помощью интеграла! Разобьем криволинейную трапецию, ограниченную осями координат и графиком функции, на бесконечно малые отрезки. Таким образом фигура окажется разделена на тонкие столбики. Сумма площадей столбиков и будет составлять площадь трапеции. Но помните, что такое вычисление даст примерный результат. Однако чем меньше и уже будут отрезки, тем точнее будет вычисление. Если мы уменьшим их до такой степени, что длина будет стремиться к нулю, то сумма площадей отрезков будет стремиться к площади фигуры. Это и есть определенный интеграл, который записывается так:

Точки а и b называются пределами интегрирования.

Кстати! Для наших читателей сейчас действует скидка 10% на

Правила вычисления интегралов для чайников

Свойства неопределенного интеграла

Как решать неопределенный интеграл? Здесь мы рассмотрим свойства неопределенного интеграла, которые пригодятся при решении примеров.

• Производная от интеграла равна подынтегральной функции:

• Константу можно выносить из-под знака интеграла:

• Интеграл от суммы равен сумме интегралов. Верно также для разности:

Свойства определенного интеграла

• Линейность:

• Знак интеграла изменяется, если поменять местами пределы интегрирования:

• При любых точках a , b и с :

Мы уже выяснили, что определенный интеграл - это предел суммы. Но как получить конкретное значение при решении примера? Для этого существует формула Ньютона-Лейбница:

Примеры решения интегралов

Ниже рассмотрим несколько примеров нахождения неопределенных интегралов. Предлагаем самостоятельно разобраться в тонкостях решения, а если что-то непонятно, задавайте вопросы в комментариях.

Для закрепления материала посмотрите видео о том, как решаются интегралы на практике. Не отчаиваетесь, если интеграл не дается сразу. Обратитесь в профессиональный сервис для студентов, и любой тройной или криволинейный интеграл по замкнутой поверхности станет вам по силам.

Сегодня слово «Интеграл» можно услышать довольно часто, причем, зачастую, в самых неожиданных местах, например на биржевом канале по телевизору, или по новостям. Нередко мы слышим словосочетание «интегральные показатели» , слово «интегрированный», «интегративный» и тому подобное. Ну, по большому счету, чиновники и телеведущие, вообще, очень любят разные умные слова, правда вряд ли они понимают их истинное значение. А мы сегодня поговорим о том, что же такое интеграл, какие виды интеграла существуют и в чем их отличия.

Что такое интеграл

Интеграл- это латинское слово, которое пришло к нам из античности, и означает оно «Целый», или «Полный». То есть, ясно, что если про некий объект, например, сосуд молока говорили «интегер», это означало, что он полный, и молока в нем сколько было, столько и осталось.

Со временем это слово стали употреблять в совершенно разных дисциплинах- в философии, политике, экономике, в алгебре и геометрии. Но наиболее простую интерпретацию интегралу дает математика.

Итак, интеграл -это некая сумма отдельных частей. Вот наиболее простые примеры для, более четкого понимания сути этого термина:

1. Предмет — это интеграл(сумма) молекул.
2. Лист в клетку — это интеграл(сумма) клеток.
3. Солнечная система — это интеграл(сумма) солнца и планет.
4. Общество — это интеграл людей.
5. Отрезок- это интеграл (сумма) метров. Если маленький отрезок, то сантиметров, миллиметров или микроскопических отрезков.
6. Площадь какой-либо поверхности — это интеграл квадратных метров, квадратных сантиметров или миллиметров, а также микроскопических площадей.
7. Объем- это интеграл кубических метров или, как их еще называют — литров.

Что такое определенный и неопределенный интегралы?

Начнем с определенного, так как его смысл поддается пониманию легче.

Геометрия изучает площади . Например, если вы хотите поклеить дома обои, вам надо знать площадь стен, чтобы узнать, сколько обоев вы должны купить. Тогда вы просто умножаете длину стены на высоту и получаете ее площадь. В данном случае, эта площадь является интегралом квадратных метров или сантиметров, в зависимости от того, в каких единицах вы ее измеряли. Но поверхности, площадь которых нам требуется вычислить далеко не всегда имеют форму прямоугольника, квадрата, или даже круга. В большинстве случаев — это сложные фигуры с волнистыми сторонами. Наиболее распространенный пример — площадь фигуры под кривой, имеющей уравнение y=1/x . Дело в том, что найти ее площадь при помощи обычных формул, которыми мы находим площадь квадрата, круга или даже сферы — невозможно. Для этой цели был разработан определенный интеграл.

Суть метода в том, что нашу сложную фигуру нужно разбить на очень узкие прямоугольники, настолько узкие, что высота каждых двух соседних практически равна. Ясно, что по сути, можно уменьшать толщину этих прямоугольников бесконечно, поэтому для обозначения их толщины используется размер dx. X — это координата, а приставка d — это обозначение бесконечно уменьшаемой величины. Поэтому, когда мы пишем dx — это значит, что мы берем отрезок по оси x , длина которого очень мала, практически равна нулю.

Итак, мы уже условились, что площадь любой фигуры- это интеграл квадратных метров или любых других фигур с более мелкими площадями. Тогда наша фигура, площадь которой мы ищем, представляет собой интеграл или сумму тех бесконечно тонких прямоугольников, на которые мы ее разбили. А ее площадь- это сумма их площадей. То есть вся наша задача сводится к тому, чтобы найти площадь каждого из этих прямоугольников, а затем их все сложить- это и есть определенный интеграл.

Теперь поговорим о неопределенном интеграле. Только, для того, чтобы понять, что это такое, сначала нужно узнать о производной. Итак, начнем.

Производная — это угол наклона касательной к какому-либо графику в какой-нибудь ее точке. Иными словами — производная — это то, насколько график наклонен в данном его месте. К примеру, прямая линия в любой точке имеет один и тот же наклон, а кривая- разный, но он может повторяться. Для вычисления производной существуют специальные формулы, а процесс ее вычисления называют дифференцированием. Т.е. дифференцирование — это определение угла наклона графика в данной точке.

А для того, чтобы сделать наоборот — узнать формулу графика по углу ее наклона, прибегают к операции интегрирования, или суммирования данных обо всех точках. Интегрирование и дифференцирование- два взаимообратных процесса. Только здесь уже пользуются не тем интегралом, который был в первом пункте (для определения площади), а другим — неопределенным, то есть, не имеющим пределов.

Предположим, что нам известно, что производная некоей функции равна 5. 5 — это угол наклона графика к оси х в данной точке. Тогда, проинтегрировав производную, мы узнаем, что функция этой производной, которую еще называют первообразной — у=5х+с, где с- любое число. Для интегрирования, так же как и для дифференцирования есть специальные формулы, которые можно найти в таблицах.

Заключение

В заключение прорезюмируем, что основное отличие определенного интеграла от неопределенного — в их назначениях. Определенные интегралы используются для вычисления ограниченных параметров, таких как площадь, длина или объем, а неопределенный — при вычислении параметров, не имеющих границ, то есть функций.

Интересное видео на эту тему:

Определённым интегралом от непрерывной функции f (x ) на конечном отрезке [a , b ] (где ) называется приращение какой-нибудь её первообразной на этом отрезке. (Вообще, понимание заметно облегчится, если повторить тему неопределённого интеграла) При этом употребляется запись

Как видно на графиках внизу (приращение первообразной функции обозначено ), определённый интеграл может быть как положительным, так и отрицательным числом (Вычисляется как разность между значением первообразной в верхнем пределе и её же значением в нижнем пределе, т. е. как F (b ) - F (a )).

Числа a и b называются соответственно нижним и верхним пределами интегрирования, а отрезок [a , b ] – отрезком интегрирования.

Таким образом, если F (x ) – какая-нибудь первообразная функция для f (x ), то, согласно определению,

(38)

Равенство (38) называется формулой Ньютона-Лейбница . Разность F (b ) – F (a ) кратко записывают так:

Поэтому формулу Ньютона-Лейбница будем записывать и так:

(39)

Докажем, что определённый интеграл не зависит от того, какая первообразная подынтегральной функции взята при его вычислении. Пусть F (x ) и Ф(х ) – произвольные первообразные подынтегральной функции. Так как это первообразные одной и той же функции, то они отличаются на постоянное слагаемое: Ф(х ) = F (x ) + C . Поэтому

Тем самым установлено, что на отрезке [a , b ] приращения всех первообразных функции f (x ) совпадают.

Таким образом, для вычисления определённого интеграла необходимо найти любую первообразную подынтегральной функции, т.е. сначала следует найти неопределённый интеграл. Постоянная С из последующих вычислений исключается. Затем применяется формула Ньютона-Лейбница: в первообразную функцию подставляется значение верхнего предела b , далее - значение нижнего предела a и вычисляется разность F(b) - F(a) . Полученное число и будет определённым интегралом. .

При a = b по определению принимается

Пример 1.

Решение. Сначала найдём неопределённый интеграл:

Применяя формулу Ньютона-Лейбница к первообразной

(при С = 0), получим

Однако при вычислении определённого интеграла лучше не находить отдельно первообразную, а сразу записывать интеграл в виде (39).

Пример 2. Вычислить определённый интеграл

Решение. Используя формулу

Свойства определённого интеграла

Теорема 2. Величина определённого интеграла не зависит от обозначения переменной интегрирования , т.е.

(40)

Пусть F (x ) – первообразная для f (x ). Для f (t ) первообразной служит та же функция F (t ), в которой лишь иначе обозначена независимая переменная. Следовательно,

На основании формулы (39) последнее равенство означает равенство интегралов

Теорема 3. Постоянный множитель можно выносить за знак определённого интеграла , т.е.

(41)

Теорема 4. Определённый интеграл от алгебраической суммы конечного числа функций равен алгебраической сумме определённых интегралов от этих функций , т.е.

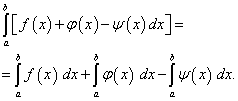(42)

Теорема 5. Если отрезок интегрирования разбит на части, то определённый интеграл по всему отрезку равен сумме определённых интегралов по его частям , т.е. если

(43)

Теорема 6. При перестановке пределов интегрирования абсолютная величина определённого интеграла не меняется, а изменяется лишь его знак , т.е.

(44)

Теорема 7 (теорема о среднем). Определённый интеграл равен произведению длины отрезка интегрирования на значение подынтегральной функции в некоторой точке внутри его , т.е.

(45)

Теорема 8. Если верхний предел интегрирования больше нижнего и подынтегральная функция неотрицательна (положительна), то и определённый интеграл неотрицателен (положителен), т.е. если

Теорема 9. Если верхний предел интегрирования больше нижнего и функции и непрерывны, то неравенство

можно почленно интегрировать , т.е.

(46)

Свойства определённого интеграла позволяют упрощать непосредственное вычисление интегралов.

Пример 5. Вычислить определённый интеграл

Используя теоремы 4 и 3, а при нахождении первообразных – табличные интегралы (7) и (6), получим

Определённый интеграл с переменным верхним пределом

Пусть f (x ) – непрерывная на отрезке [a , b ] функция, а F (x ) – её первообразная. Рассмотрим определённый интеграл

(47)

а через t обозначена переменная интегрирования, чтобы не путать её с верхней границей. При изменении х меняется и опредёленный интеграл (47), т.е. он является функцией верхнего предела интегрирования х , которую обозначим через Ф (х ), т.е.

(48)

Докажем, что функция Ф (х ) является первообразной для f (x ) = f (t ). Действительно, дифференцируя Ф (х ), получим

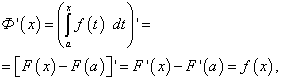
так как F (x ) – первообразная для f (x ), а F (a ) – постояная величина.

Функция Ф (х ) – одна из бесконечного множества первообразных для f (x ), а именно та, которая при x = a обращается в нуль. Это утверждение получается, если в равенстве (48) положить x = a и воспользоваться теоремой 1 предыдущего параграфа.

Вычисление определённых интегралов методом интегрирования по частям и методом замены переменной

где, по определению, F (x ) – первообразная для f (x ). Если в подынтегральном выражении произвести замену переменной

то в соответствии с формулой (16) можно записать

В этом выражении

первообразная функция для

В самом деле, её производная, согласно правилу дифференцирования сложной функции , равна

Пусть α и β – значения переменной t , при которых функция

принимает соответственно значения a и b , т.е.

Но, согласно формуле Ньютона-Лейбница, разность F (b ) – F (a ) есть

В дифференциальном исчислении рассматривались задачи, решение которых требовало отыскания производной данной функции. В ряде случаев приходится решать обратную задачу: по заданной производной отыскивать функцию, которую дифференцировали. Задачи такого рода решаются в разделе математического анализа, называемом интегральным исчислением . Методы интегрального исчисления позволяют решать задачи на вычисление площадей плоских фигур, длин дуг, объемов тел и другие геометрические и физические задачи.

Пример 1. Пусть скорость {v} движения точки в момент времени {t} равна 2t . Найдем выражение для координаты точки в момент времени {t} (точка движется по прямой).

Решение. Известно, что v=\frac{dx}{dt} . Так как в данном случае \frac{dx}{dt}=2t , то ответом к задаче могут быть функции x=t^2; x=t^2+3 и т.д.; в общем виде ответ на поставленный вопрос записывается в виде x=t^2+C , где C - произвольная постоянная.

Из приведенного примера видно, что обратная задача имеет бесконечное множество решений. Чтобы получить определенный закон движения, необходимо знать, например, положение точки в момент времени t=0 . Если при t=0 имеем x=0 , то 0=0+C , и потому C=0 .

Перемещение точки за промежуток времени равно (b^2+C)-(a^2+C)=b^2-a^2 , и, следовательно, оно не зависит от C .

Первообразная функция

Определение 1. Пусть на некотором промежутке X задана функция y=f(x) . Функция y=F(x) называется первообразной для f(x) на этом промежутке, если для всех x\in X

F"(x)=f(x).

Термин "первообразная" был введен французским математиком Ж. Л. Лагранжем (1736-1813).

Следующая теорема позволяет свести нахождение всех первообразных данной функции к отысканию одной из них.

Теорема 1. Если функция y=f(x) имеет на промежутке X первообразную F(x) , то и все функции вида F(x)+C будут для нее первообразными на том же промежутке. Обратно, любая первообразная \Phi(x) для функции y=f(x),\,x\in X , может быть представлена в виде \Phi(x)+C , где F(x) - одна из первообразных функций, а C - произвольная постоянная.

Доказательство. По определению первообразной имеем F"(x)=f(x) . Учитывая, что производная постоянной равна нулю, получаем:

(F(x)+C)"=F"(x)+C"=F"(x)=f(x).

Это и означает, что F(x)+C является первообразной для y=f(x) на промежутке X .

Покажем теперь, что если функция y=f(x) задана на промежутке F и F(x) - одна из первообразных для f(x) , то любая первообразная \Phi(x) может быть представлена в виде \Phi(x)=F(x)+C .

В самом деле, по определению первообразной имеем: \Phi"(x)=f(x) и F"(x)=f(x) . Но две функции, имеющие на промежутке X равные производные, отличаются лишь на постоянное слагаемое. Значит, \Phi(x)=F(x)+C , что и требовалось доказать.

Определения неопределенного и определенного интегралов

Определение 2. Множество всех первообразных для функции y=f(x) на промежутке X называется неопределенным интегралом для f(x) и обозначается .

Функцию y=f(x) называют подынтегральной функцией для \textstyle{\int f(x)\,dx} , а произведение f(x)\,dx - подынтегральным выражением .

Таким образом, \int f(x)\,dx=\{F(x)+C\mid C\in \mathbb{R}\} . На практике принята более короткая запись: \int f(x)\,dx=F(x)+C .

Часто говорят: "взять неопределенный интеграл" или "вычислить неопределенный интеграл", понимая под этим следующее: найти множество всех первообразных для подынтегральной функции.

Мы видели, что если функция имеет хоть одну первообразную, то она имеет бесконечно много первообразных. На практике часто приходится искать разность значений первообразной в точках b и a . Эта разность не зависит от выбора произвольной постоянной C . В самом деле, если \Phi(x)=F(x)+C , то

\Phi(b)-\Phi(b)=(F(b)+C)-(F(a)+C)=F(b)-F(a).

Итак, \Phi(b)-\Phi(b)=F(b)-F(a) , что и требовалось доказать.

Поскольку разность значений первообразной в точках b и a не зависит от того, какую именно первообразную функции y=f(x) мы выбираем, эту разность называют определенным интегралом от функции по отрезку .

Определение 3. Пусть функция y=f(x) задана на отрезке и имеет на нем первообразную y=F(x) . Разность F(b)-F(a) называют определенным интегралом функции f(x) по отрезку и обозначают \textstyle{\int\limits_{a}^{b}f(x)\,dx} . Итак,

\int\limits_{a}^{b}f(x)\,dx=F(b)-F(a).

Разность F(b)-F(a) записывают в виде \Bigl.{F(x)}\Bigr|_{a}^{b} , тогда \textstyle{\int\limits_{a}^{b} f(x)\,dx= \Bigl.{F(x)}\Bigr|_{a}^{b}} . Числа a и b называют пределами интегрирования .

Например, y=\frac{x^3}{3} одна из первообразных для функции y=x^2 . Поэтому

\int\limits_{a}^{b}x^2\,dx=\left.{\frac{x^3}{3}}\right|_{a}^{b}=\frac{b^3}{3}-\frac{a^3}{3}=\frac{b^3-a^3}{3}\,.

Остановимся на геометрическом смысле введенных понятий. Пусть F(x) является первообразной для f(x) . Угловой коэффициент касательной в каждой точке графика функции y=F(x) равен F"(x) , т. е. f(x) . Поэтому задача о нахождении первообразной геометрически означает следующее: зная угловой коэффициент касательной в каждой точке, найти кривую . Так как при параллельном переносе вдоль оси ординат угловой коэффициент касательной в точке с заданной абсциссой не изменяется, то, найдя одну такую кривую, все остальные искомые кривые получают из нее параллельным переносом в направлении оси ординат. Это семейство кривых (рис. 1) и представляет собой геометрическую иллюстрацию неопределенного интеграла.

Определенный интеграл \textstyle{\int\limits_{a}^{b}f(x)\,dx=F(b)-F(a)} показывает изменение ординаты каждой из кривых y=F(x)+C при переходе от точки a к точке b . Так как все эти кривые получаются друг из друга параллельным переносом в направлении оси ординат, то указанное изменение ординаты для всех кривых одно и то же (рис. 2).

Рассмотрим задачи, решение которых сводится к вычислению определенных интегралов.

Задача 1. Пусть точка M движется по прямой и пусть известна скорость v=v(t) движения этой точки в любой момент {x} времени {t} промежутка . Найдем перемещение {s} точки M за этот промежуток времени.

Решение. Мы знаем, что если x=x(t) - закон движения точки, то v(t)=x"(t) . Поэтому x(t) - одна из первообразных для функции v=v(t) . Но перемещение {s} точки M за промежуток времени равно разности ее координат в моменты времени b и a , т.е. равно x(b)-x(a) . Иными словами, это перемещение равно разности значений первообразной для функции v=v(t) в моменты времени b и a . Таким образом, s=\textstyle{\int\limits_{a}^{b}v(t)\,dt} .

Так, например, скорость тела при свободном падении выражают формулой v=gt . В этом случае путь, пройденный падающим телом за b секунд с начала падения, вычисляется так:

S=\int\limits_{0}^{b}gt\,dt= \left.{\frac{gt^2}{2} }\right|_{0}^{b}= \frac{gb^2}{2}\,.

Задача 2. Найдем площадь криволинейной трапеции aA\,Bb , ограниченной осью абсцисс, прямыми x=a и x=b и графиком непрерывной на функции y=f(x) , принимающей на этом отрезке только неотрицательные значения (рис. 3).

Прежде чем переходить к решению задачи, заметим, что здесь мы используем наглядное представление о площади плоской фигуры (более детально вопрос об определении площади).

Решение. Обозначим через S(x) площадь криволинейной трапеции aA\,Nx\,(a

Дадим абсциссе x приращение \Delta x (положим для определенности \Delta x>0 ), тогда площадь получит приращение \Delta S . Обозначим через m наименьшее значение функции y=f(x) на отрезке , а через M - наибольшее значение той же функции на том же отрезке. Ясно, что тогда m\cdot\Delta x\leqslant\Delta S\leqslant M\cdot\Delta x , а значит, m\leqslant\frac{\Delta S}{\Delta x}\leqslant M .

Если \Delta x\to 0 , то в силу непрерывности функции y=f(x) будем иметь:

\lim_{\Delta x\to0}m=\lim_{\Delta x\to0}=f(x).

Значит, существует и \lim\frac{\Delta S}{\Delta x} , причем этот предел равен f(x) . Таким образом, S"(x)=f(x) .

Полученное равенство означает, что S(x) - одна из первообразных для функции y=f(x) . Поскольку прямая x=a "отсекает" от трапеции aABb фигуру нулевой площади, то S(a)=0 . С другой стороны, S(b) - площадь всей криволинейной трапеции aABb . Значит, искомая площадь S равна (S(b)-S(a)) , т.е. равна разности значений одной из первообразных для функции y=f(x) в точках b и a . Это означает, что

\boldsymbol{S=\int\limits_{a}^{b}f(x)\,dx\,.}

Пример 2. Найдем площадь фигуры, ограниченной осью абсцисс и одной полуволной синусоиды y=\sin{x} (рис. 4).

Решение. Искомая площадь S выражается формулой \textstyle{S= \int\limits_{0}^{\pi}\sin{x}\,dx} . Одной из первообразных для функции y=\sin{x} является (-\cos{x}) , так как (-\cos{x})"=\sin{x}) . Значит,

S= \int\limits_{0}^{\pi}\sin{x}\,dx=\Bigl.{-\cos{x}}\Bigr|_{0}^{\pi}= -(\cos\pi-\cos0)=-(-1-1)=2.

В заключение данного пункта остановимся на двух свойствах неопределенного интеграла, легко получающихся из определения.

1°. Дифференциал от неопределенного интеграла равен подынтегральному выражению, а производная неопределенного интеграла равна подынтегральной функции:

D\!\left(\int f(x)\,dx\right)= f(x)\,dx,\quad \left(\int f(x)\,dx\right)"=f(x).

Доказательство. Так как \textstyle{\int f(x)\,dx=F(x)+C} , где F"(x)=f(x) , то \textstyle{\left(\int f(x)\,dx\right)"= \bigl(F(x)+C\bigr)"=F"(x)+C"=f(x)} .

Но тогда \textstyle{d\!\left(\int f(x)\,dx\right)= \left(\int f(x)\,dx\right)"dx=f(x)\,dx} .

Это утверждение часто используется для проверки результата интегрирования. Пусть, например, нужно показать, что

\int5x\,dx=\frac{5}{2}\,x^2+C\quad (C=\text{const}).

Дифференцируя правую часть равенства, получим подынтегральную функцию:

\left(\frac{5}{2}\,x^2+C\right)"=\frac{5}{2}\cdot 2x+0=5x . Значит, \int5x\,dx=\frac{5}{2}\,x^2+C .

2°. Неопределенный интеграл от производной некоторой функции равен этой функции, сложенной с произвольной постоянной:

\int F"(x)\,dx=F(x)+C.

Доказательство. Так как \bigl(F(x)+C\bigr)"=F"(x) , то по определению неопределенного интеграла \textstyle{\int F"(x)\,dx=F(x)+C} , что и требовалось доказать.

Учитывая, что F"(x)\,dx=d\bigl(F(x)\bigr) , свойство 2° можно записать и так: \textstyle{\int d\bigl(F(x)\bigr)=F(x)+C} .

Таблица основных интегралов

Пользуясь свойством 1° из предыдущего пункта, можно по таблице производных составить таблицу основных интегралов. Например, так как

(\sin{x})"=\cos{x} , то \int\cos{x}\,dx=\sin{x}+C. .

Докажем, что \int\dfrac{1}{x}\,dx=\ln|x|+C . В самом деле, если x>0 , то |x|=x и, следовательно, \bigl(\ln|x|\bigr)"=\bigl(\ln{x}\bigr)"=\frac{1}{x}\, .

Если x<0 , то |x|=-x и, следовательно, \bigl(\ln|x|\bigr)"=\bigl(\ln(-x)\bigr)"= \frac{1}{-x}\cdot(-1)=\frac{1}{x} .

Итак, \bigl(\ln|x|\bigr)"=\frac{1}{x} , а значит, \int\frac{1}{x}\,dx=\ln|x|+C .

Эту формулу можно применять или на открытом луче (0;+\infty) , или на открытом луче (-\infty;0) .

Таблица основных интегралов

\begin{aligned}&\boldsymbol{1.}\quad \int 0\,dx=C; &\quad &\boldsymbol{2.}\quad \int 1\,dx=\int dx=x+C;\\ &\boldsymbol{3.}\quad \int x^{a}\,dx=\frac{x^{a+1}}{a+1}+C,~a\ne-1; &\quad &\boldsymbol{4.}\quad \int \frac{dx}{x}=\ln{x}+C;\\ &\boldsymbol{5.}\quad \int \frac{dx}{a^2+x^2}=\frac{1}{a}\operatorname{arctg}\frac{x}{a}+C; &\quad &\boldsymbol{6.}\quad \int \frac{dx}{\sqrt{a^2-x^2}}=\arcsin\frac{x}{a}+C;\\ &\boldsymbol{7.}\quad \int a^x\,dx=\frac{a^x}{\ln a}+C; &\quad &\boldsymbol{8.}\quad \int e^x\,dx=e^x+C;\\ &\boldsymbol{9.}\quad \int \sin{x}\,dx=-\cos{x}+C; &\quad &\boldsymbol{10.}\quad \int \cos{x}\,dx=\sin{x}+C;\\ &\boldsymbol{11.}\quad \int \frac{dx}{\sin^2x}=-\operatorname{ctg}x+C; &\quad &\boldsymbol{12.}\quad \int \frac{dx}{\cos^2x}=\operatorname{tg}x+C;\\ &\boldsymbol{13.}\quad \int \frac{dx}{x^2-a^2}=\frac{1}{2a}\ln\! \left|\frac{x-a}{x+a}\right|+C; &\quad &\boldsymbol{14.}\quad \int \frac{dx}{\sqrt{x^2\pm a^2}}=\ln \bigl|x+\sqrt{x^2\pm a^2}\bigr|+C.\\ \end{aligned}

Заметим, что переменную x , входящую в эти формулы, можно заменить любой другой. Например, вместо формулы \textstyle{\int\cos{x}\,dx= \sin{x}+C} можно написать \textstyle{\int\cos{t}\,dt= \sin{t}+C} и т.д.

Пример 3. Вычислим неопределённые интегралы от различных дробей:

\mathsf{1)}~\int\frac{dx}{\sqrt{x}}\,;\quad \mathsf{2)}~\int\frac{dx}{x^2+16}\,;\quad \mathsf{3)}~\int\frac{dx}{x^2-16}\,;\quad \mathsf{4)}~\int\frac{dx}{\sqrt{3-x^2}}\,;\quad \mathsf{5)}~\int\frac{dx}{\sqrt{x^2-3}}\,.

Решение. 1) Воспользуемся формулой 3 из таблицы интегралов:

\int\frac{dx}{\sqrt{x}}= \int x^{-1/3}\,dx= \frac{x^{-1/3+1}}{-1/3+1}+C= \frac{3}{2}\,x^{2/3}+C;

2) Воспользуемся формулой 5: \int\frac{dx}{x^2+16}= \int\frac{dx}{x^2+4^2}=\frac{1}{4} \operatorname{arctg}\frac{x}{2}+C; .

3) Воспользуемся формулой 12: \int\frac{dx}{x^2-16}= \int\frac{dx}{x^2-4^2}= \frac{1}{8}\ln\!\left|\frac{x-4}{x+4}\right|+C; .

4) Воспользуемся формулой 6: \int\frac{dx}{\sqrt{3-x^2}}= \int\frac{dx}{\sqrt{(\sqrt{3})^2-x^2}}= \arcsin\frac{x}{\sqrt{3}}+C; .

5) Воспользуемся формулой 13: \int\frac{dx}{\sqrt{x^2-3}}= \ln\Bigl|x+\sqrt{x^2-3}\Bigr|+C. .