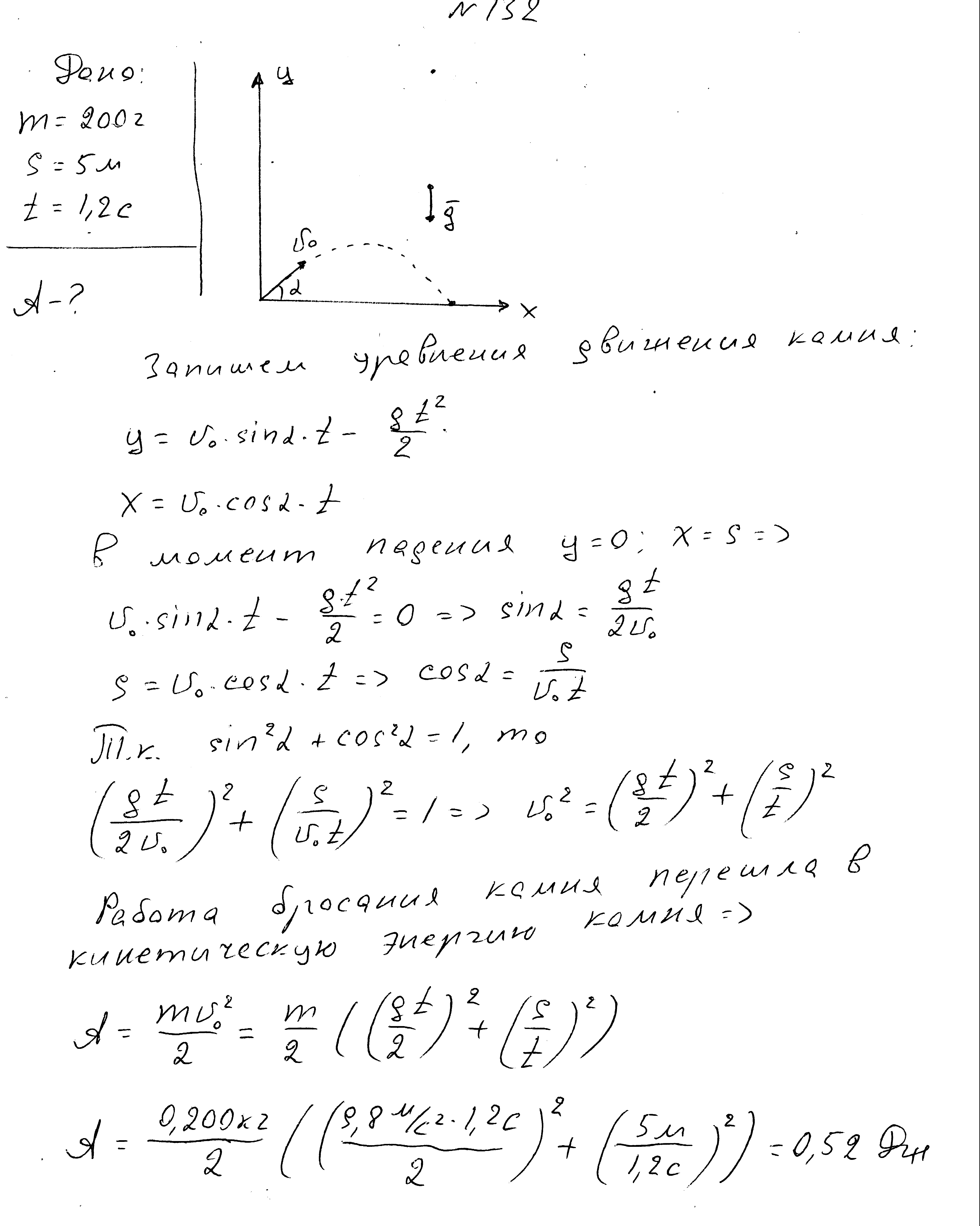Proučavanje kretanja tijela bačenog pod uglom u odnosu na horizontalu. Kretanje tijela bačenog pod uglom u odnosu na horizontalu! Fizika: kretanje tijela bačenog pod uglom u odnosu na horizontalu

Ako je tijelo bačeno pod uglom prema horizontu, tada u letu na njega djeluju sila gravitacije i sila otpora zraka. Ako se zanemari sila otpora, jedina preostala sila je gravitacija. Prema tome, zbog 2. Newtonovog zakona, tijelo se kreće ubrzanjem jednakom ubrzanju gravitacije; projekcije ubrzanja na koordinatne ose ax = 0, ay = - g.

Slika 1. Kinematske karakteristike tijela bačenog pod uglom u odnosu na horizontalu

Svako složeno kretanje materijalne tačke može se predstaviti kao superpozicija nezavisnih kretanja duž koordinatnih osa, a u pravcu različitih osa tip kretanja se može razlikovati. U našem slučaju, kretanje letećeg tela može se predstaviti kao superpozicija dva nezavisna kretanja: ravnomerno kretanje duž horizontalne ose (X-osa) i jednoliko ubrzano kretanje duž vertikalne ose (Y-osa) (Sl. 1) .

Stoga se projekcije brzine tijela mijenjaju s vremenom na sljedeći način:

gdje je $v_0$ početna brzina, $(\mathbf \alpha )$ je ugao bacanja.

Uz naš izbor ishodišta, početne koordinate (slika 1) su $x_0=y_0=0$. tada dobijamo:

(1)

Analizirajmo formule (1). Odredimo vrijeme kretanja bačenog tijela. Da bismo to učinili, postavimo y koordinatu jednaku nuli, jer u trenutku sletanja visina tela je nula. Odavde dobijamo za vrijeme leta:

Druga vremenska vrijednost na kojoj je visina nula je nula, što odgovara trenutku bacanja, tj. ova vrijednost ima i fizičko značenje.

Domet leta dobijamo iz prve formule (1). Domet leta je vrijednost x koordinate na kraju leta, tj. u vrijeme jednako $t_0$. Zamjenom vrijednosti (2) u prvu formulu (1) dobijamo:

Iz ove formule se vidi da se najveći domet leta postiže pri kutu bacanja od 45 stepeni.

Maksimalna visina dizanja bačenog tijela može se dobiti iz druge formule (1). Da biste to učinili, morate u ovu formulu zamijeniti vrijednost vremena jednaku polovini vremena leta (2), jer Maksimalna je visina leta u sredini putanje. Provodeći proračune, dobijamo

Iz jednačina (1) može se dobiti jednačina putanje tijela, tj. jednačina koja povezuje x i y koordinate tijela tokom kretanja. Da biste to učinili, trebate izraziti vrijeme iz prve jednačine (1):

i zamijenite ga u drugu jednačinu. tada dobijamo:

Ova jednadžba je jednadžba putanje kretanja. Može se vidjeti da je ovo jednačina parabole sa granama prema dolje, što je označeno znakom “-” ispred kvadratnog člana. Treba imati na umu da su kut bacanja $\alpha $ i njegove funkcije ovdje jednostavno konstante, tj. konstantni brojevi.

Tijelo je bačeno brzinom v0 pod uglom $(\mathbf \alpha )$ prema horizontu. Vrijeme leta $t = 2 s$. Do koje visine Hmax će se tijelo podići?

$$t_B = 2 s$$ $$H_max - ?$$

Zakon kretanja tijela ima oblik:

$$\left\( \begin(array)(c) x=v_(0x)t \\ y=v_(0y)t-\frac(gt^2)(2) \end(array) \right.$ $

Početni vektor brzine formira ugao $(\mathbf \alpha )$ sa OX osom. dakle,

\ \ \

Kamen je bačen sa vrha planine pod uglom = 30$()^\circ$ prema horizontu početnom brzinom od $v_0 = 6 m/s$. Ugao nagnute ravni = 30$()^\circ$. Koliko daleko od tačke bacanja će kamen pasti?

$$ \alpha =30()^\circ$$ $$v_0=6\ m/s$$ $$S - ?$$

Postavimo ishodište koordinata u tačku bacanja, OX - duž nagnute ravni nadole, OY - okomito na nagnutu ravan nagore. Kinematske karakteristike kretanja:

zakon kretanja:

$$\left\( \begin(array)(c) x=v_0t(cos 2\alpha +g\frac(t^2)(2)(sin \alpha \ )\ ) \\ y=v_0t(sin 2 \alpha \ )-\frac(gt^2)(2)(cos \alpha \ ) \end(niz) \right.$$ \

Zamjenom rezultirajuće vrijednosti $t_V$, nalazimo $S$:

Ostale su 3 sekunde do kraja finalne utakmice košarkaškog turnira Olimpijskih igara u Minhenu 1972. godine. Amerikanci - reprezentacija SAD-a - već su slavili svoju pobjedu! Naš tim - reprezentacija SSSR-a - pobedio je sa oko 10 poena razlike protiv velikog Dream Teama...

Nekoliko minuta prije kraja utakmice. Ali, pošto je na kraju izgubila svu prednost, već je gubila jedan poen 49:50. Onda se desilo neverovatno! Ivan Edeško ubacuje loptu iza krajnje linije preko celog terena ispod američkog obruča, gde naš centar Aleksandar Belov prima loptu, okružen dvojicom protivnika, i ubacuje je u koš. 51:50 – mi smo olimpijski prvaci!!!

Kao dijete tada sam doživljavao najjače emocije - prvo razočarenje i ogorčenost, pa ludo oduševljenje! Emocionalno sjećanje na ovu epizodu urezano je u moju svijest do kraja života! Pogledajte video na internetu na zahtjev "Zlatno bacanje Aleksandra Belova", nećete požaliti.

Amerikanci tada nisu priznali poraz i odbili su primiti srebrne medalje. Da li je moguće za tri sekunde uraditi ono što su naši igrači uradili? Prisjetimo se fizike!

U ovom članku ćemo pogledati kretanje tijela bačenog pod kutom prema horizontu, kreirati program u Excelu za rješavanje ovog problema s različitim kombinacijama ulaznih podataka i pokušati odgovoriti na gore postavljeno pitanje.

Ovo je prilično poznat problem u fizici. U našem slučaju, tijelo bačeno pod uglom u odnosu na horizontalu je košarkaška lopta. Izračunat ćemo početnu brzinu, vrijeme i putanju lopte koju je Ivan Edeshko bacio preko cijelog terena i koja je pala u ruke Aleksandra Belova.

Matematika i fizika košarkaškog leta.

Formule i proračuni predstavljeni u nastavku suexcel univerzalni su za širok spektar problema o tijelima bačenim pod uglom u odnosu na horizont i koja lete duž paraboličke putanje bez uzimanja u obzir utjecaja zračnog trenja.

Dijagram proračuna je prikazan na donjoj slici. Pokrenite MS Excel ili OOo Calc.

Početni podaci:

1. Pošto se nalazimo na planeti Zemlji i razmatramo balistički problem - kretanje tela u Zemljinom gravitacionom polju, prvo što ćemo uraditi je da zapišemo glavnu karakteristiku gravitacionog polja - ubrzanje slobodnog pada g u m/s 2

do ćelije D3: 9,81

2. Dimenzije košarkaškog terena su 28 metara dužine i 15 metara širine. Horizontalna udaljenost lopte od gotovo cijelog terena do prstena od suprotne osnovne linije x pisati u metrima

do ćelije D4: 27,000

3. Ako pretpostavimo da je Edeshko izveo bacanje sa visine od oko dva metra, a Belov je uhvatio loptu baš negdje u nivou obruča, onda je sa košarkaškim obručem visine 3,05 metara vertikalna udaljenost između tačaka polaska i dolaska od lopte će biti 1 metar. Zapišimo vertikalni pomak y u metrima

do ćelije D5: 1,000

4. Prema mojim mjerenjima na video snimku, ugao lansiranja lopte α 0 iz Edeshovih ruku nije prelazio 20°. Unesite ovu vrijednost

do ćelije D6: 20,000

Rezultati proračuna:

Osnovne jednadžbe koje opisuju kretanje tijela bačenog pod uglom prema horizontu bez uzimanja u obzir otpora zraka:

x =v 0*cos α 0 *t

y =v 0*sin α 0 *t -g *t 2 /2

5. Hajde da izrazimo vreme t iz prve jednačine, zamijenite je drugom i izračunajte početnu brzinu lopte v 0 u m/s

u ćeliji D8: =(D3*D4^2/2/COS (RADIANS(D6))^2/(D4*TAN (RADIANS(D6)) -D5))^0.5 =21,418

v 0 =(g *x 2 /(2*(cosα 0 ) 2 *(x *tgα 0 -y )) 0.5

6. Vrijeme leta lopte od Edeškovih ruku do Belovih ruku t Izračunajmo u sekundama, znajući sada v 0 , iz prve jednačine

u ćeliji D9: =D4/D8/COS (RADIANS(D6)) =1,342

t = x /(v 0 * cosα 0 )

7. Nađimo ugao smjera brzine leta lopte α i na tački putanje koja nas zanima. Da bismo to učinili, pišemo početni par jednadžbi u sljedećem obliku:

y =x *tgα 0 -g *x 2 /(2*v 0 2*(cosα 0 ) 2)

Ovo je jednadžba parabole - putanja leta.

Moramo pronaći ugao nagiba tangente na parabolu u tački koja nas zanima - to će biti ugao α i. Da biste to učinili, uzmite derivaciju, koja je tangenta kuta tangente:

y' =tgα 0 -g *x /(v 0 2*(cosα 0 ) 2)

Izračunajmo ugao dolaska lopte u Belove ruke α i u stepenima

u ćeliji D10: =ATAN (TAN (RADIANS(D6)) -D3*D4/D8^2/COS (RADIANS(D6))^2)/PI()*180 =-16,167

α i = arctgy ’ = arctg(tgα 0 — g * x /(v 0 2 *(cosα 0 ) 2))

Izračun u Excelu je u osnovi završen.

Ostale opcije plaćanja:

Koristeći napisani program, možete brzo i jednostavno izvršiti proračune sa drugim kombinacijama početnih podataka.

Neka zadana horizontala x = 27 metara , vertikalno y = Domet leta 1 metar i početna brzina v 0 = 25 m/s.

Moramo pronaći vrijeme leta t i uglovi odlaska α 0 i dolazak α i

Koristimo MS Excel uslugu “Odabir parametara”. Više puta sam detaljno objasnio kako ga koristiti u nekoliko članaka na blogu. Možete pročitati više o korištenju ove usluge.

Postavljamo vrijednost u ćeliji D8 na 25.000 mijenjajući vrijednost u ćeliji D6 tako što ćemo je odabrati. Rezultat je na slici ispod.

Izvorni podaci u ovoj verziji proračuna u Excel-u (kao i u prethodnoj) označeni su plavim okvirima, a rezultati crvenim pravokutnim okvirima!

Postavka u tabeliExcel neku vrijednost od interesa u jednoj od ćelija sa svijetložutim punjenjem odabirom promijenjene vrijednosti u jednoj od ćelija sa svijetlotirkiznim ispunom, općenito možete dobiti deset različitih opcija za rješavanje problema kretanja tijela bačenog na ugao prema horizontu za deset različitih skupova originalnih podataka!!!

Odgovor na pitanje:

Odgovorimo na pitanje postavljeno na početku članka. Lopta koju je poslao Ivan Edeško do Belova je, prema našim proračunima, odletela za 1,342 sekunde. Alexander Belov je uhvatio loptu, sletio, skočio i bacio. Imao je dosta vremena za sve ovo - 1,658 sekundi! Ovo je zaista dovoljno slobodnog vremena! Detaljan pregled video snimka potvrđuje gore navedeno. Naši igrači su imali tri sekunde da loptu sa svoje krajnje linije isporuče do protivničke table i ubace je u obruč, ispisavši svoja imena zlatom u istoriji košarke!

molim poštovanjem autorski rad preuzimanje datoteka nakon pretplate za najave članaka!

Slobodan pad predstavlja poseban slučaj jednoliko ubrzanog kretanja bez početne brzine. Ubrzanje ovog kretanja jednako je ubrzanju gravitacije, koje se naziva i ubrzanje gravitacije. Za ovo kretanje vrijede formule:

u t
g
h- visina sa koje tijelo pada
t- vrijeme tokom kojeg se pad nastavio

Bilješka:

• Otpor zraka se ne uzima u obzir u ovim formulama.
• Ubrzanje gravitacije ima zadatu vrijednost (9,81 (m/s?)) u blizini zemljine površine. Vrijednost g se mijenja na drugim udaljenostima od Zemljine površine!

Kretanje tijela bačenog okomito prema gore

Tijelo bačeno okomito prema gore kreće se ravnomjerno sporo početnom brzinom u0 i ubrzanje a = -g. Kretanje tijela tokom vremena t predstavlja visinu podizanja h.Za ovo kretanje vrijede sljedeće formule:

U0- početna brzina kretanja tijela
U- brzina kojom tijelo pada nakon vremena t
g- ubrzanje slobodnog pada, 9,81 (m/s?)
h- visina na koju će se tijelo vremenom podići t
t- vrijeme

Brzina tijela na određenoj visini:

Maksimalna visina podizanja:

Vrijeme za podizanje do maksimalne visine:

Zbrajanje pokreta usmjerenih pod uglom jedan prema drugom.

Tijelo može istovremeno sudjelovati u nekoliko translacijskih pokreta. Budući da su ubrzanje, brzina i pomak vektorske veličine, mogu se sabirati prema zakonima vektorskog (geometrijskog) sabiranja. One. prema pravilu paralelograma.

Rezultirajuća vrijednost bilo koje karakteristike kretanja može se izračunati.

ako:
Gore- rezultujuća trenutna brzina,
U1- trenutna brzina prvog pokreta,
U2- trenutna brzina drugog pokreta,
? - ugao formiran od vektora brzina u1 I u2,
Zatim, koristeći kosinus teoremu, dobijamo:

Ako se pokreti 1 i 2 odvijaju pod pravim kutom jedno u odnosu na drugo, formula se pojednostavljuje jer

Kretanje tijela vodoravno bačenog.

Gibanje tijela vodoravno bačenog je kombinacija dvaju gibanja međusobno okomitih jedno na drugo:
- horizontalno (ujednačeno) kretanje,
- okomito (slobodan pad)

Jednadžba putanje tijela bačenog vodoravno

Ako konstruišemo putanju tela bačenog horizontalno u koordinatnom sistemu xy, uzimajući točku bacanja kao ishodište koordinata, a smjer ordinatne ose poklapa se sa smjerom vektora ubrzanja slobodnog pada, tada koordinate svake tačke putanje predstavljaju kretanje tijela u horizontalnom smjeru (kretanje konstantnom brzinom U0) i u vertikalnom smjeru (jednako ubrzano kretanje s ubrzanjem g)

x, y- koordinate tijela,
u0
g
t- vrijeme putovanja (s)

Jednadžba putanje tijela bačenog horizontalno kao što slijedi:

g i početnu brzinu tijela u0 su konstantne veličine, zatim koordinata y proporcionalno kvadratu x, tj. trajektorija kretanja je parabola, čiji je vrh u početnoj tački kretanja.

Vektorski položaj tijela bačenog vodoravno, formula

Položaj svake tačke putanje tijela bačenog horizontalno može se odrediti vektorom položaja r, što predstavlja rezultirajući pomak:

ili Vektor položaja:

x-koordinata:

Y-koordinata:

Napomena: Otpor zraka se ne uzima u obzir u formulama.

Jednačina kretanja tijela bačenog pod uglom u odnosu na horizontalu.

Koordinate točke putanje opisane su jednadžbama:

x, y- koordinate tijela
U0- početna brzina tijela (m/s)
? - ugao pod kojim je tijelo bačeno prema horizontu (°)
g- ubrzanje slobodnog pada 9,81 (m/s2)
t- vrijeme putovanja (s)

Iz formula preko parametra t izvodimo opšte jednadžba kretanja tijela bačenog pod uglom u odnosu na horizontalu

Od ubrzanja gravitacije g, ? - ugao pod kojim je tijelo bačeno prema horizontu i početna brzina tijela u0 su konstantne veličine, zatim koordinata y proporcionalno kvadratu x, tj. trajektorija kretanja je parabola, početna tačka je na jednoj od njenih grana, a vrh parabole je tačka najveće elevacije tela.

Vrijeme izlaska na maksimalnu visinu tijela bačenog pod uglom prema horizontu.

Vrijeme podizanja do maksimalne visine određuje se iz uslova da je vertikalna komponenta trenutne brzine nula

iz ove jednačine dobijamo:

U0- početna brzina tijela (m/s),
?
g- ubrzanje slobodnog pada 9,81 (m/s2),
thmax- vrijeme za podizanje na maksimalnu visinu (s)

Udaljenost tijela bačenog pod uglom u odnosu na horizontalu.

Domet bacanja ili radijus oštećenja određena formulama za ukupno vrijeme kretanja i formulom za koordinate tijela

zamjena tsmax u izraz i pojednostavljenje dobijamo:

U0- početna brzina tijela (m/s),
? - ugao pod kojim je tijelo bačeno prema horizontu (°),
g- ubrzanje slobodnog pada 9,81 (m/s2),
tsmax- ukupno vrijeme putovanja (s)

Kretanje tijela bačenog pod uglom u odnosu na horizontalu

Razmotrimo kretanje tijela bačenog brzinom V 0, čiji je vektor usmjeren pod uglom α prema horizontu, u ravnini XOY, postavljajući tijelo u trenutku bacanja u ishodište koordinata, kao što je prikazano na slici 1.

U nedostatku sila otpora, kretanje tijela bačenog pod uglom prema horizontu može se smatrati posebnim slučajem krivolinijskog kretanja pod utjecajem gravitacije. Primjena Newtonovog 2. zakona

Slika 1 je usmjerena prema gore, u slučaju kada je os OY usmjerena prema dolje, tada je projekcija vektora

2 a na osi op-amp će biti pozitivan(čitajući uslove zadataka, sami odaberite smjer osi, ako to nije navedeno u uvjetima).

Vrijednosti projekcija vektora ubrzanja a na osi OX i OU daju razlog za izradu

sljedeći izlaz:

∙ tijelo bačeno pod uglom u odnosu na horizontalu istovremeno sudjeluje u dva pokreta - jednoliko horizontalno i jednoliko promjenjivo duž

Za jednoliko promjenjivo kretanje, ovisnosti brzine i pomaka o vremenu date su jednadžbama:

koordinate tijela u trenutku t.

Tokom njegovog kretanja t (od trenutka bacanja do trenutka pada na isti

nivo) tijelo se podiže na maksimalnu visinu hmax, spušta se s njega i odleti od točke bacanja na udaljenosti L (domet leta) - vidi sliku 1.

1) Vrijeme kretanja tijela t može se naći uzimajući u obzir vrijednosti koordinata tijela Sy in

Zamjenom vrijednosti Voy i (14) u drugu jednačinu sistema (13) dobijamo

2) Domet leta L može se pronaći, uzimajući u obzir vrijednosti koordinata tijela Sh in

početni trenutak vremena i u trenutku t (vidi sliku 1)

Zamjenom vrijednosti Vox i (17) u prvu jednačinu sistema (13) dobijamo

3) Maksimalna visina dizanja h max može se naći s obzirom na vrijednost

brzina tijela V u tački maksimalnog podizanja tijela

Poređenje vrijednosti (16) i (22) daje osnovu za zaključak

· vrijeme kretanja do visine maksimalnog podizanja tijela (t pod ) jednako je vremenu spuštanja tijela (tp) sa ove visine i jednako je polovini vremena cjelokupnog kretanja tijela od trenutka bacanja do trenutka pada na isti nivo

Proučavanje kretanja tijela bačenog brzinom V 0, čiji je vektor usmjeren pod uglom α prema horizontali, u ravni XOY, vrlo je jasno na kompjuterskom modelu

"Slobodni pad tijela" u kolekciji kompjuterskih modela "Otvorena fizika"

Kompanija PHYSIKON. U ovom modelu možete postaviti različite početne uslove.

Na primjer, slučaj koji smo razmatrali mora biti specificiran (komanda "Obriši") sa početnim uvjetom h = 0 i odabranim V0 i α. Komanda "Start" će pokazati kretanje tijela i dati sliku putanje kretanja i smjera vektora brzine tijela u fiksnim vremenskim trenucima.

Fig.2. Dijaloški prozor kompjuterskog modela "Slobodan pad tijela" u sekciji

"Mehanika"; tijelo se kreće od početka i pada na istom nivou.

Ako se stanje problema razlikuje od slučaja koji smo razmatrali, onda je to neophodno

da biste riješili problem, birajući smjer osi, postavite tijelo u početni trenutak

vrijeme, oslikavaju putanju tijela do tačke pada, dakle

određivanjem koordinata tijela u početnom i konačnom trenutku vremena. Onda

koristiti jednadžbe (3), (5), (8) i (9) kao osnovu za rješenje o kojima se raspravljalo gore

algoritam za rešavanje problema.

Razmotrimo posebne slučajeve.

6 1. Telo je odbačeno velikom brzinom V 0 , čiji je vektor usmjeren pod uglomα to

horizonta, sa visine h i pao je na udaljenosti L od tačke bacanja. y do inicijala

a vrijednosti preostalih koordinata bit će odabrane na isti način kao što smo odabrali.

Fig.3. Dijaloški prozor kompjuterskog modela "Slobodan pad tijela" u sekciji

"Mehanika"; tijelo se kreće od tačke h = 50m i pada na nulti nivo.

2. Telo je bačeno horizontalno brzinom V 0 sa visine h i ono je palo na rastojanje L od tačke bacanja. Razlika od slučaja koji smo razmatrali je u tome što su vrijednosti koordinata tijela S y u početnom trenutku će takođe biti određen jednačinom (25),

a vrijednosti preostalih koordinata bit će odabrane na isti način kao što smo odabrali. Ali u ovom slučaju, početna brzina tijela u projekciji na osu OU jednaka je nuli (pošto je α = 0), tj.

projekcije vektora početne brzine na ose OX i OU su jednake

Fig.4. Dijaloški prozor kompjuterskog modela "Slobodan pad tijela" u sekciji

"Mehanika"; tijelo bačeno horizontalno kreće se od tačke h = 50m i pada na nulti nivo.

Ispod su uvjeti problema i skenirana rješenja. Ako trebate riješiti problem na ovu temu, ovdje možete pronaći sličan uvjet i analogno riješiti svoj. Učitavanje stranice može potrajati neko vrijeme zbog velikog broja slika. Ako trebate rješavanje problema ili online pomoć u fizici, kontaktirajte nas, rado ćemo vam pomoći.

Princip rješavanja ovih problema je da se brzina tijela koje slobodno pada na dvije komponente - horizontalnu i vertikalnu. Horizontalna komponenta brzine je konstantna, vertikalno kretanje se odvija uz ubrzanje slobodnog pada g=9,8 m/s 2 . Može se primijeniti i zakon održanja mehaničke energije prema kojem je zbir potencijalne i kinetičke energije tijela u ovom slučaju konstantan.

Materijalna tačka se baca pod uglom u odnosu na horizont početnom brzinom od 15 m/s. Početna kinetička energija je 3 puta veća od kinetičke energije tačke u gornjoj tački putanje. Koliko se visoko podigla tačka?

Tijelo se baca pod uglom od 40 stepeni u odnosu na horizontalu početnom brzinom od 10 m/s. Pronađite udaljenost koju će tijelo preletjeti prije pada, visinu uspona u gornjoj tački putanje i vrijeme leta.

Tijelo je bačeno sa tornja visine H, pod uglom α prema horizontali, početnom brzinom v. Pronađite udaljenost od tornja do mjesta gdje je tijelo palo.

Tijelo mase 0,5 kg bačeno je sa površine Zemlje pod uglom od 30 stepeni u odnosu na horizontalu, početnom brzinom od 10 m/s. Pronađite potencijalnu i kinetičku energiju tijela nakon 0,4 s.

Materijalna tačka se izbacuje naviše sa Zemljine površine pod uglom prema horizontu početnom brzinom od 10 m/s. Odrediti brzinu tačke na visini od 3 m.

Tijelo je izbačeno naviše sa Zemljine površine pod uglom od 60 stepeni početnom brzinom od 10 m/s. Pronađite udaljenost do tačke udara, brzinu tijela na mjestu udara i vrijeme leta.

Tijelo je bačeno prema gore pod uglom u odnosu na horizontalu početnom brzinom od 20 m/s. Udaljenost do tačke pada je 4 puta veća od maksimalne visine podizanja. Pronađite ugao pod kojim je tijelo bačeno.

Tijelo se baca sa visine od 5 m pod uglom od 30 stepeni u odnosu na horizontalu početnom brzinom od 22 m/s. Pronađite domet leta tijela i vrijeme leta tijela.

Tijelo je bačeno sa Zemljine površine pod uglom prema horizontu početnom brzinom od 30 m/s. Pronađite tangencijalno i normalno ubrzanje tijela 1s nakon bacanja.

Tijelo je bačeno sa površine Zeslija pod uglom od 30 stepeni u odnosu na horizontalu početnom brzinom od 14,7 m/s. Pronađite tangencijalno i normalno ubrzanje tijela 1,25 s nakon bacanja.

Tijelo se baca pod uglom od 60 stepeni u odnosu na horizontalu početnom brzinom od 20 m/s. Nakon kojeg vremena će ugao između brzine i horizonta postati 45 stepeni?

Lopta bačena u teretani pod uglom prema horizontu,sa početnom brzinom od 20 m/s, u gornjoj tački putanje dodirnuo je plafon na visini od 8 m i pao na određenoj udaljenosti od mjesta bacanja. Pronađite ovu udaljenost i ugao pod kojim je tijelo bačeno.

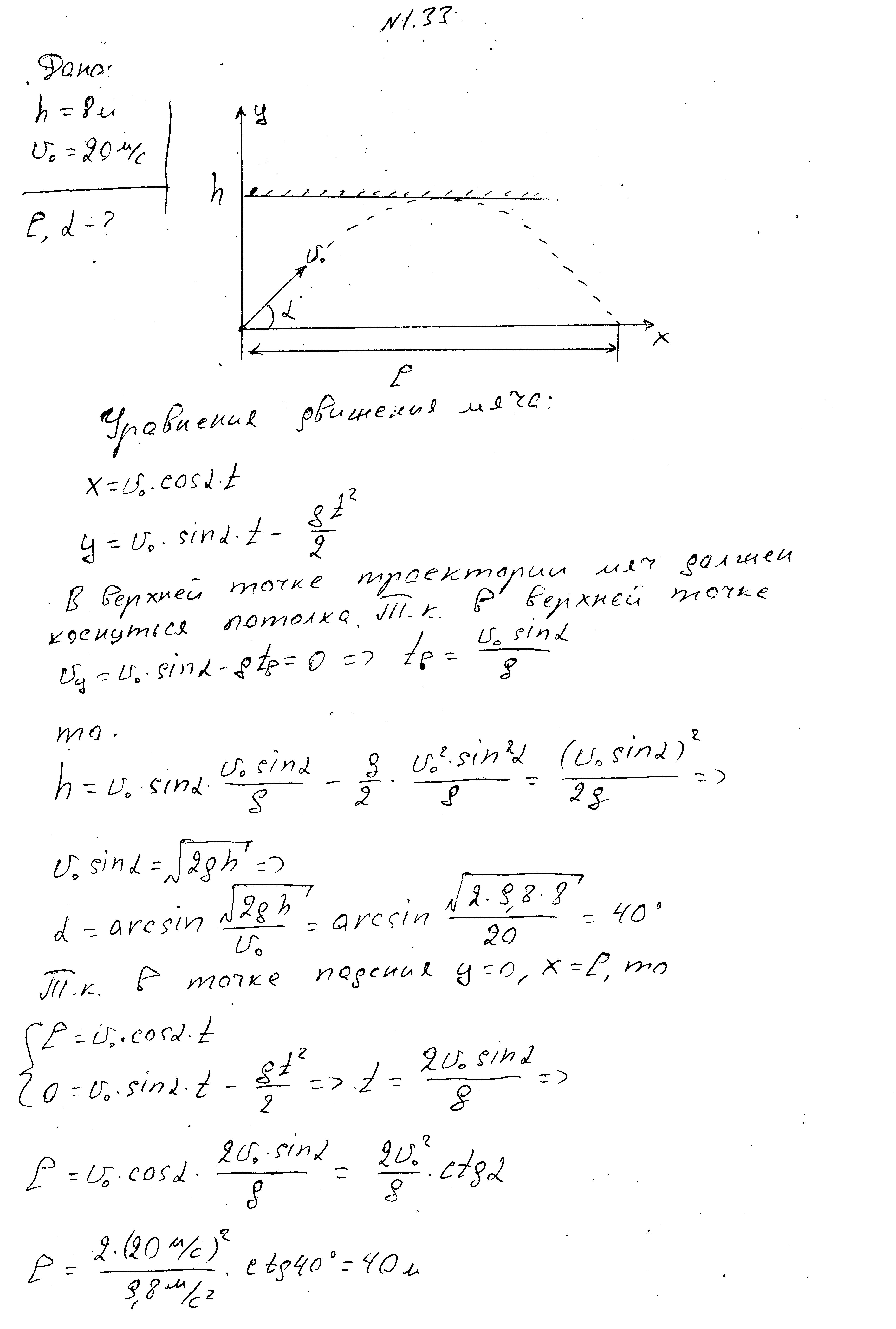
Tijelo bačeno sa površine Zemlje pod uglom prema horizontu palo je nakon 2,2 s. Pronađite maksimalnu visinu dizanja tijela.

Kamen se baca pod uglom od 30 stepeni u odnosu na horizontalu. Kamen je dva puta dostigao određenu visinu - 1 s i 3 s nakon što je bačen. Pronađite ovu visinu i početnu brzinu kamena.

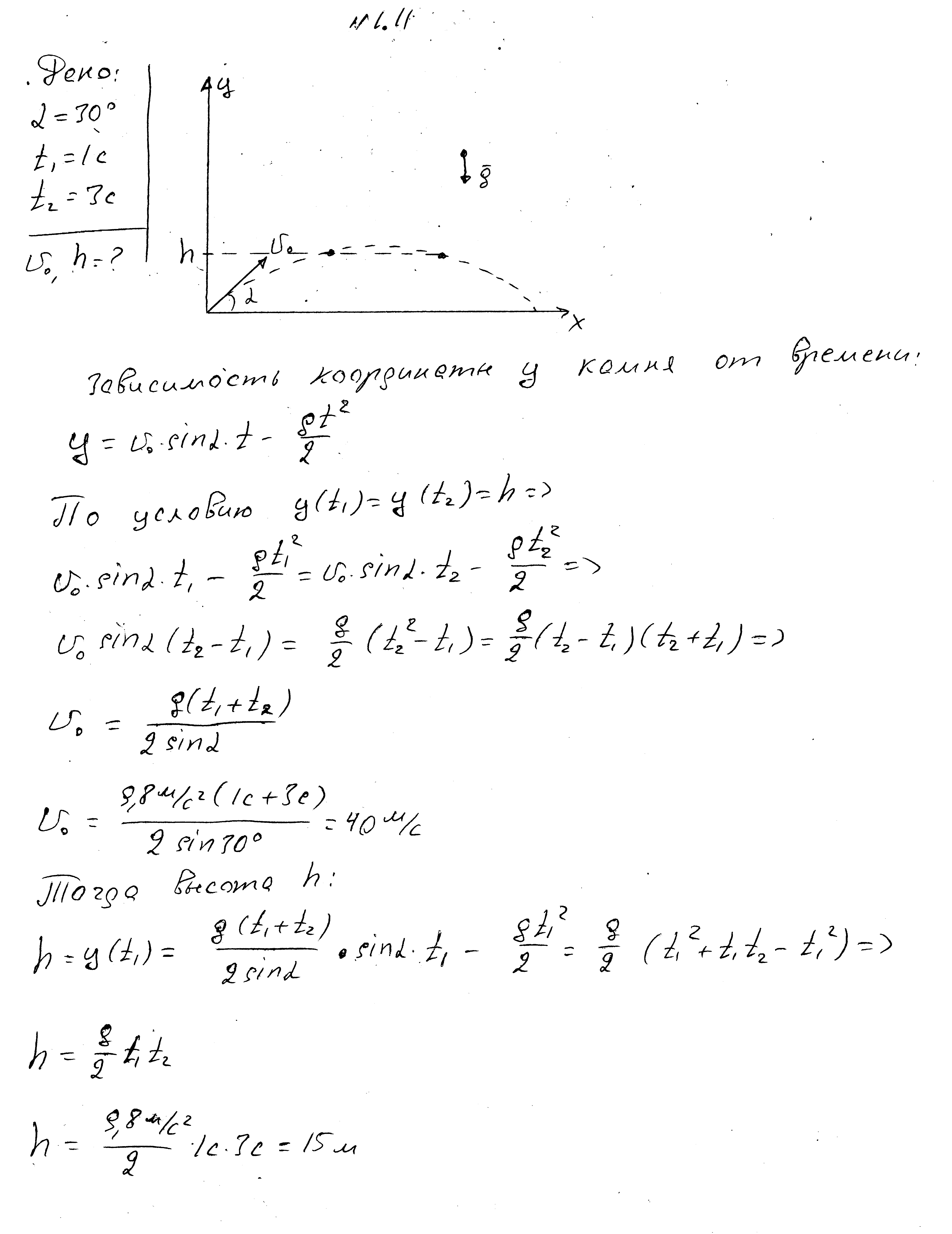
Kamen se baca pod uglom od 30 stepeni u odnosu na horizontalu početnom brzinom od 10 m/s. Pronađite udaljenost od točke bacanja do kamena nakon 4 s.

Projektil se ispaljuje u trenutku kada avion leti iznad topa, pod uglom prema horizontu, početnom brzinom od 500 m/s. Granata je pogodila avion na visini od 3,5 km 10 sekundi nakon što je ispaljena. Kolika je brzina aviona?

Topovska kugla težine 5 kg bačena je sa površine Zemlje pod uglom od 60 stepeni u odnosu na horizontalu. Energija utrošena za ubrzanje težine je 500 J. Odredite domet leta i vrijeme leta.

Tijelo se baca sa visine od 100 m pod uglom od 30 stepeni u odnosu na horizontalu početnom brzinom od 5 m/s. Pronađite domet leta tijela.

Tijelo mase 200 g, bačeno sa površine Zemlje pod uglom prema horizontu, palo je na udaljenosti od 5 m nakon vremena od 1,2 s. Nađi posao bacanja tijela.