Сумма углов треугольника. Полные уроки — Гипермаркет знаний

Доказательство

Пусть ABC" - произвольный треугольник. Проведем через вершину B прямую, параллельную прямой AC (такая прямая называется прямой Евклида). Отметим на ней точку D так, чтобы точки A и D лежали по разные стороны от прямой BC .Углы DBC и ACB равны как внутренние накрест лежащие, образованные секущей BC с параллельными прямыми AC и BD . Поэтому сумма углов треугольника при вершинах B и С равна углу ABD .Сумма всех трех углов треугольника равна сумме углов ABD и BAC . Так как эти углы внутренние односторонние для параллельных AC и BD при секущей AB , то их сумма равна 180°. Теорема доказана.

Следствия

Из теоремы следует, что у любого треугольника два угла острые. Действительно, применяя доказательство от противного , допустим, что у треугольника только один острый угол или вообще нет острых углов. Тогда у этого треугольника есть, по крайней мере, два угла, каждый из которых не меньше 90°. Сумма этих углов не меньше 180°. А это невозможно, так как сумма всех углов треугольника равна 180°. Что и требовалось доказать.

Обобщение в симплекс теории

Где -угол между i и j гранями симплекса.

Примечания

• На сфере сумма углов треугольника всегда превышает 180°, разница называется сферическим избытком и пропорциональна площади треугольника.
• В плоскости Лобачевского сумма углов треугольника всегда меньше 180°. Разность также пропорциональна площади треугольника.

См. также

Wikimedia Foundation . 2010 .

Смотреть что такое "Теорема о сумме углов треугольника" в других словарях:

Свойство многоугольников в евклидовой геометрии: Сумма углов n угольника равна 180°(n 2). Содержание 1 Доказательство 2 Замечание … Википедия

Теорема Пифагора одна из основополагающих теорем евклидовой геометрии, устанавливающая соотношение между сторонами прямоугольного треугольника. Содержание 1 … Википедия

Теорема Пифагора одна из основополагающих теорем евклидовой геометрии, устанавливающая соотношение между сторонами прямоугольного треугольника. Содержание 1 Формулировки 2 Доказательства … Википедия

Теорема косинусов обобщение теоремы Пифагора. Квадрат стороны треугольника равен сумме квадратов двух других его сторон без удвоенного произведения этих сторон на косинус угла между ними. Для плоского треугольника со сторонами a,b,c и углом α… … Википедия

У этого термина существуют и другие значения, см. Треугольник (значения). Треугольник (в евклидовом пространстве) это геометрическая фигура, образованная тремя отрезками, которые соединяют три не лежащие на одной прямой точки. Три точки,… … Википедия

Стандартные обозначения Треугольник простейший многоугольник, имеющий 3 вершины (угла) и 3 стороны; часть плоскости, ограниченная тремя точками, не лежащими на одной прямой, и тремя отрезками, попарно соединяющими эти точки. Вершины треугольника … Википедия

Древнегреческий математик. Работал в Александрии в III в. до н. э. Главный труд «Начала» (15 книг), содержащий основы античной математики элементарной геометрии, теории чисел, общей теории отношений и метода определения площадей и объёмов,… … Энциклопедический словарь

- (умер между 275 и 270 до н. э.) древнегреческий математик. Сведения о времени и месте его рождения до нас не дошли, однако известно, что Евклид жил в Александрии и расцвет его деятельности приходится на время царствования в Египте Птолемея I… … Большой Энциклопедический словарь

Геометрия, сходная с геометрией Евклида в том, что в ней определено движение фигур, но отличающаяся от евклидовой геометрии тем, что один из пяти ее постулатов (второй или пятый) заменен его отрицанием. Отрицание одного из евклидовых постулатов… … Энциклопедия Кольера

>>Геометрия: Сумма углов треугольника. Полные уроки

ТЕМА УРОКА: Сумма углов треугольника.

Цели урока:

• Закрепление и проверка знаний учащихся по теме: «Сумма углов треугольника»;
• Доказательство свойства углов треугольника;
• Применение этого свойства при решении простейших задач;
• Использование исторического материала для развития познавательной активности учащихся;
• Привитие навыка аккуратности при построении чертежей.

Задачи урока:

• Проверить умение учащихся решать задачи.

План урока:

1. Треугольник;
2. Теорема о сумме углов треугольника;
3. Пример задач.

Треугольник.

Файл:O.gif Треугольник - простейший многоугольник, имеющий 3 вершины (угла) и 3 стороны; часть плоскости, ограниченная тремя точками, и тремя отрезками, попарно соединяющими эти точки.
Трём точкам пространства, не лежащим на одной прямой, соответствует одна и только одна плоскость.
Любой многоугольник можно разбить на треугольники - этот процесс называется триангуляция .
Существует раздел математики, целиком посвящённый изучению закономерностей треугольников - Тригонометрия .

Теорема о сумме углов треугольника.

Файл:T.gif Теорема о сумме углов треугольника - классическая теорема евклидовой геометрии, утверждает что cумма углов треугольника равна 180°.

Доказательство":

Пусть дан Δ ABC. Проведем через вершину B прямую, параллельную (AC) и отметим на ней точку D так, чтобы точки A и D лежали по разные стороны от прямой BC. Тогда угол (DBC) и угол (ACB) равны как внутренние накрест лежащие при параллельных прямых BD и AC и секущей (BC). Тогда сумма углов треугольника при вершинах B и C равна углу (ABD). Но угол (ABD) и угол (BAC) при вершине A треугольника ABC являются внутренними односторонними при параллельных прямых BD и AC и секущей (AB), и их сумма равна 180°. Следовательно, сумма углов треугольника равна 180°. Теорема доказана.

Следствия.

Внешний угол треугольника равен сумме двух углов треугольника, не смежных с ним.

Доказательство:

Пусть дан Δ ABC. Точка D лежит на прямой AC так, что A лежит между C и D. Тогда BAD – внешний к углу треугольника при вершине A и A + BAD = 180°. Но A + B + C = 180°, и, следовательно, B + C = 180° – A. Отсюда BAD = B + C. Следствие доказано.

Следствия.

Внешний угол треугольника больше любого угла треугольника, не смежного с ним.

Задача.

Внешним углом треугольника называется угол, смежный с каким-нибудь углом этого треугольника. Докажите, что внешний угол треугольника равен сумме двух углов треугольника, не смежных с ним.
(Рис.1)

Решение:

Пусть в Δ АВС ∠DАС – внешний (Рис.1). Тогда ∠DАС=180°-∠ВАС (по свойству смежных углов), по теореме о сумме углов треугольника ∠В+∠С =180°-∠ВАС. Из этих равенств получим ∠DАС=∠В+∠С

Интересный факт:

Сумма углов треугольника":

В геометрии Лобачевского сумма углов треугольника всегда меньше 180. В геометрии Эвклида она всегда равна 180 . В геометрии Римана сумма углов треугольника всегда больше 180.

Из истории математики:

Евклид (III в до н.э) в труде «Начала» приводит такое определение: «Параллельные суть прямые, которые находятся в одной плоскости и, будучи продолжены в обе стороны неограниченно, ни с той, ни с другой стороны между собой не встречаются».
Посидоний (I в до н.э) «Две прямые, лежащие в одной плоскости, равноотстоящие друг от друга»
Древнегреческий учёный Папп (III в до н.э) ввёл символ параллельных прямых- знак =. Впоследствии английский экономист Рикардо (1720-1823) этот символ использовал как знак равенства.
Только в XVIII веке стали использовать символ параллельности прямых - знак ||.
Ни на миг не прерывается живая связь между поколениями, ежедневно мы усваиваем опыт, накопленный нашими предками. Древние греки на основе наблюдений и из практического опыта делали выводы, высказывали гипотезы, а затем, на встречах учёных – симпозиумах (буквально « пиршество») – эти гипотезы пытались обосновать и доказать. В то время и сложилось утверждение: « В споре рождается истина».

Вопросы:

1. Что такое треугольник?
2. Что гласит теорема о сумме углов треугольника?
3. Чему равен внешний угол треугольника?

Сумма углов треугольника - важная, но достаточно простая тема, которую проходят в 7 классе на геометрии. Тема состоит из теоремы, короткого доказательства и нескольких логичных следствий. Знание этой темы помогает в решении геометрических задач при последующем изучении предмета.

Теорема - чему равны сложенные между собой углы произвольного треугольника?

Теорема гласит - если взять любой треугольник вне зависимости от его вида, сумма всех углов неизменно составит 180 градусов. Доказывается это следующим образом:

• для примера берут треугольник АВС, через расположенную на вершине точку В проводят прямую линию и обозначают ее, как «а», прямая «а» при этом строго параллельна стороне АС;
• между прямой «а» и сторонами АВ и ВС обозначают углы, маркируя их цифрами 1 и 2;
• угол 1 признают равным углу А, а угол 2 - равным углу С, поскольку эти углы считаются накрест лежащими;
• таким образом, сумма между углами 1, 2 и 3 (который обозначается на месте угла В) признается равной развернутому углу с вершиной В - и составляет 180 градусов.

Если сумма углов, обозначенных цифрами, составляет 180 градусов, то и сумма углов А, В и С признается равной 180 градусам. Это правило верно для любого треугольника.

Что следует из геометрической теоремы

Принято выделять несколько следствий из приведенной теоремы.

• Если в задаче рассматривается треугольник с прямым углом, то один из его углов будет по умолчанию равен 90 градусам, а сумма острых углов также составит 90 градусов.
• Если речь идет о прямоугольном равнобедренном треугольнике, то его острые углы, в сумме составляющие 90 градусов, по отдельности будут равны 45 градусам.
• Равносторонний треугольник состоит из трех равных углов, соответственно, каждый из них будет равен 60 градусам, а в сумме они составят 180 градусов.
• Внешний угол любого треугольника будет равняться сумме между двумя внутренними углами, не прилегающими к нему.

Можно вывести следующее правило - в любом из треугольников есть как минимум два острых угла. В некоторых случаях треугольник состоит из трех острых углов, а если их только два, то третий угол будет тупым либо прямым.

Разделы: Математика

Презентация . (Слайд 1)

Тип урока: урок изучения нового материала.

Цели урока:

• Образовательные :
  • рассмотреть теорему о сумме углов треугольника,
  • показать применение теоремы при решении задач.
• Воспитательные :
  • воспитание положительного отношения учащихся к знаниям,
  • воспитывать в учащихся средствами урока уверенность в своих силах.
• Развивающие :
  • развитие аналитического мышления,
  • развитие «умений учиться»: использовать знания, умения и навыки в учебном процессе,
  • развитие логического мышления, способности четко формулировать свои мысли.

Оборудование: интерактивная доска, презентация, карточки.

ХОД УРОКА

I. Организационный момент

– Сегодня на уроке мы вспомним определения прямоугольного, равнобедренного, равностороннего треугольников. Повторим свойства углов треугольников. Применяя свойства внутренних односторонних и внутренних накрест лежащих углов докажем теорему о сумме углов треугольника и научимся применять ее при решении задач.

II. Устно (Слайд 2)

1) Найти на рисунках прямоугольный, равнобедренный, равносторонний треугольники.
2) Дать определение этим треугольникам.
3) Сформулировать свойства углов равностороннего и равнобедренного треугольника.

4) На рисунке KE II NH. (слайд 3)

– Укажите секущие для этих прямых
– Найти внутренние односторонние углы, внутренние накрест лежащие углы, назвать их свойства

III. Объяснение нового материала

Теорема. Сумма углов треугольника равна 180 о

По формулировке теоремы, ребята строят чертеж, записывают условие, заключение. Отвечая на вопросы, самостоятельно доказывают теорему.

Дано: Доказать:

Доказательство:

1. Через вершину В треугольника проведем прямую BD II AC.
2. Указать секущие для параллельных прямых.
3. Что можно сказать об углах CBD и ACB? (сделать запись)
4. Что мы знаем об углах CAB и ABD? (сделать запись)
5. Заменим угол CBD углом ACB
6. Сделать вывод.

IV. Закончи предложение. (Слайд 4)

1. Сумма углов треугольника равна …
2. В треугольнике один из углов равен, другой, третий угол треугольника равен …
3. Сумма острых углов прямоугольного треугольника равна …
4. Углы равнобедренного прямоугольного треугольника равны …
5. Углы равностороннего треугольника равны...
6. Если угол между боковыми сторонами равнобедренного треугольника равен 1000, то углы при основании равны …

V. Немного истории. (Слайды 5-7)

Треугольник. Остроугольный, тупоугольный и прямоугольный треугольник.

Катеты и гипотенуза. Равнобедренный и равносторонний треугольник.

Сумма углов треугольника.

Внешний угол треугольника. Признаки равенства треугольников.

Замечательные линии и точки в треугольнике: высоты, медианы,

биссектрисы,срединны e перпендикуляры, ортоцентр,

центр тяжести, центр описанного круга, центр вписанного круга.

Теорема Пифагора. Соотношение сторон в произвольномтреугольнике.

Треугольник – это многоугольник с тремя сторонами (или тремя углами). Стороны треугольника обозначаются часто малыми буквами, которые соответствуют заглавным буквам, обозначающим противоположные вершины.

Если все три угла острые (рис.20 ), то это остроугольный треугольник . Если один из углов прямой ( C, рис.21), то это прямоугольный треугольник ; стороны a , b , образующие прямой угол, называются катетами ; сторона c , противоположная прямому углу, называется гипотенузой . Если один из углов тупой ( B, рис.22), то это тупоугольный треугольник.


Треугольник ABC (рис.23) - равнобедренный , если две его стороны равны (a = c ); эти равные стороны называются боковыми , третья сторона называется основанием треугольника. Треугольник ABC (рис.24) – равносторонний , если все его стороны равны (a = b = c ). В общем случае (a ≠ b ≠ c ) имеем неравносторонний треугольник.

Основные свойства треугольников. В любом треугольнике:

1. Против большей стороны лежит больший угол, и наоборот.

2. Против равных сторон лежат равные углы, и наоборот.

В частности, все углы в равностороннем треугольнике равны.

3. Сумма углов треугольника равна 180 º .

Из двух последних свойств следует, что каждый угол в равностороннем

треугольнике равен 60 º.

4. Продолжая одну из сторон треугольника (AC, рис.25), получаем внешний

угол BCD. Внешний угол треугольника равен сумме внутренних углов,

не смежных с ним : BCD = A + B.

5. Любая сторона треугольника меньше суммы двух других сторон и больше

их разности (a < b + c , a > b – c ;b < a + c , b > a – c ;c < a + b ,c > a – b ).

Признаки равенства треугольников.

Треугольники равны, если у них соответственно равны:

a ) две стороны и угол между ними;

b ) два угла и прилегающая к ним сторона;

c ) три стороны.

Признаки равенства прямоугольных треугольников.

Д ва прямоугольных треугольника равны, если выполняется одно из следующих условий:

1) равны их катеты;

2) катет и гипотенуза одного треугольника равны катету и гипотенузе другого;

3) гипотенуза и острый угол одного треугольника равны гипотенузе и острому углу другого;

4) катет и прилежащий острый угол одного треугольника равны катету и прилежащему острому углу другого;

5) катет и противолежащий острый угол одного треугольника равны катету и противолежащему острому углу другого.

Замечательные линии и точки в треугольнике.

Высота треугольника - это перпендикуляр, опущенный из любой вершины на противоположную сторону ( или её продолжение ). Эта сторона называется основанием треугольника . Три высоты треугольника всегда пересекаются в одной точке , называемой ортоцентром треугольника. Ортоцентр остроугольного треугольника (точка O , рис.26) расположен внутри треугольника, а ортоцентр тупоугольного треугольника (точка O , рис.27) – снаружи; ортоцентр прямоугольного треугольника совпадает с вершиной прямого угла.

Медиана – это отрезок , соединяющий любую вершину треугольника с серединой противоположной стороны. Три медианы треугольника (AD , BE , CF , рис.28) пересекаются в одной точке O , всегда лежащей внутри треугольника и являющейся его центром тяжести. Эта точка делит каждую медиану в отношении 2:1, считая от вершины.

Биссектриса – это отрезок биссектрисы угла от вершины до точки пересечения с противоположной стороной. Три биссектрисы треугольника (AD , BE , CF , рис.29) пересекаются в одной точке О, всегда лежащей внутри треугольника и являющейся центром вписанного круга (см. раздел «Вписанные и описанные многоугольники»).

Биссектриса делит противоположную сторону на части, пропорциональные прилегающим сторонам ; например, на рис.29 AE : CE = AB : BC .

Срединный перпендикуляр – это перпендикуляр, проведенный из средней точки отрезка (стороны). Три срединных перпендикуляра треугольника АВС (KO , MO , NO , рис.30 ) пересекаются в одной точке О, являющейся центром описанного круга (точки K , M , N – середины сторон треугольника ABC ).

В остроугольном треугольнике эта точка лежит внутри треугольника; в тупоугольном – снаружи; в прямоугольном - в середине гипотенузы. Ортоцентр, центр тяжести, центр описанного и центр вписанного круга совпадают только в равностороннем треугольнике.

Теорема Пифагора. В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.

Доказательство теоремы Пифагора с очевидностью следует из рис.31. Рассмотрим прямоугольный треугольник ABC с катетами a , b и гипотенузой c .

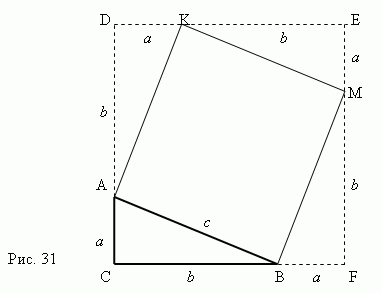
Построим квадрат AKMB , используя гипотенузу AB как сторону. Затем продолжим стороны прямоугольного треугольника ABC так, чтобы получить квадрат CDEF , сторона которого равна a + b . Теперь ясно, что площадь квадрата CDEF равна (a + b ) 2 . С другой стороны, эта площадь равна сумме площадей четырёх прямоугольных треугольников и квадрата AKMB , то есть

c 2 + 4 (ab / 2) = c 2 + 2 ab ,

отсюда ,

c 2 + 2 ab = (a + b ) 2 ,

и окончательно имеем:

c 2 = a 2 + b 2 .

Соотношение сторон в произвольном треугольнике.

В общем случае (для произвольного треугольника) имеем:

c 2 = a 2 + b 2 – 2ab · cos C,

где C – угол между сторонами a и b .