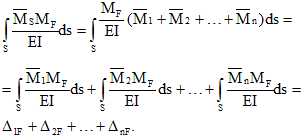Izračunajte ploščati statično nedoločen palični sistem. Izračun statično nedoločenih sistemov z metodo sil

Statično nedoločene sisteme imenujemo palični sistemi, za določanje reakcij nosilcev, pri katerih samo enačbe ravnotežja niso dovolj. S kinematičnega vidika so to takšni palični sistemi, katerih število prostostnih stopinj je manjše od števila vezi. Za razkritje statične nedoločenosti takih sistemov je potrebno sestaviti dodatne enačbe združljivosti deformacij. Število takih enačb je določeno s številom statične nedoločenosti paličnega sistema. Slika 8.14 prikazuje primere statično nedoločenih nosilcev in okvirjev.

Žarek, prikazan na sliki 8.14b, se imenuje neprekinjenožarek. To ime izhaja iz dejstva, da vmesna podpora podpira le žarek. Na mestu podpore nosilec ni prerezan s tečajem, tečaj ni vrezan v telo nosilca. Zato vpliv napetosti in deformacij, ki jih ima nosilec na levem razponu, vpliva tudi na desni razpon. Če v telo nosilca na mestu vmesne podpore vrežemo šarnir, bo posledično sistem postal statično determiniran - iz enega nosilca bomo dobili dva med seboj neodvisna nosilca, od katerih bo vsak statično determiniran. . Treba je opozoriti, da so neprekinjeni nosilci manj materialno intenzivni v primerjavi z razcepljenimi nosilci, saj bolj racionalno porazdelijo upogibne momente po svoji dolžini. V zvezi s tem se neprekinjeni nosilci pogosto uporabljajo v gradbeništvu in inženirstvu. Vendar pa zvezni nosilci, ki so statično nedoločeni, zahtevajo posebno tehniko izračuna, ki vključuje uporabo sistemskih deformacij.

Preden nadaljujemo z izračunom statično nedoločenih sistemov, se je treba naučiti, kako določiti stopnjo njihove statične nedoločenosti. Eno najpreprostejših pravil za določanje stopnje statične nedoločenosti je naslednje:

, (8.3)

kje  število vezi, naloženih na strukturo;  število možnih neodvisnih ravnotežnih enačb, ki jih je mogoče sestaviti za obravnavani sistem.

Za določitev stopnje statične nedoločenosti sistemov, prikazanih na sliki 8.14, uporabimo enačbo (8.3).

Nosilec, prikazan na sliki 8.14a, je nekoč statično nedoločen, saj ima na levem kraku tri vezice, na desnem kraku pa eno vezico. Za tak žarek obstajajo samo tri neodvisne ravnotežne enačbe. Tako je stopnja statične nedoločenosti žarka
. Kontinuirani nosilec, prikazan na sliki 8.14b, je prav tako enkrat statično nedoločen, saj ima dve vezi na levem nosilcu in po eno povezavo na vmesnem nosilcu in na desnem nosilcu - skupaj štiri povezave. Torej stopnja njegove statične nedoločenosti
.

Okvir, prikazan na sl. 8.14c, je trikrat statično nedoločen, saj ima v nosilcih šest vezi. Za ta okvir obstajajo samo tri neodvisne ravnotežne enačbe. Tako je stopnja statične negotovosti za ta okvir iz enačbe (8.3):
. Stopnja statične nedoločenosti okvirja, prikazanega na sliki 8.18, d, je enaka štirim, saj ima okvir sedem povezav na nosilcih. Zato je stopnja njegove statične nedoločenosti enaka
.

Pravilo (8.3) za določanje stopnje statične nedoločenosti se uporablja samo za enostavne sisteme. V bolj zapletenih primerih to pravilo ne deluje. Slika 8.15 prikazuje okvir, katerega stopnje statične negotovosti ni mogoče določiti z enačbo (8.3).

Navzven je sistem, prikazan na sliki 8.15, petkrat statično nedoločen. To je enostavno ugotoviti z uporabo enačbe (8.3): od šestih zunanjih vezi (tri v odseku A, tri v odseku B in dve v odseku C) se odštejejo tri možne ravnotežne enačbe. Vendar ima ta sistem tudi notranjo statično nedoločenost. Z enačbo (8.3) ni mogoče upoštevati notranje statične nedoločenosti. Preden preidemo na določanje stopnje statične nedoločenosti okvirja, prikazanega na sliki 8.15, uvedemo več definicij. Prva od teh definicij vključuje pojem enostavnega tečaja.

Enostavno imenovan tečaj, ki povezuje dve palici (slika 8.16).

Sl.8.16. preprost tečaj

Imenuje se tečaj, ki povezuje več palic težko(Slika 8.17).

Sl.8.17. kompleksen tečaj

Število preprostih tečajev, ki lahko nadomestijo en kompleksen tečaj, se določi po formuli:

, (8.4)

kje
- število palic, vključenih v vozlišče.

Kompleksni tečaj, prikazan na sliki 8.17, preračunamo v število preprostih tečajev z uporabo formule (8.4):
. Tako lahko zapleten tečaj, prikazan na sliki 8.17, nadomestimo s štirimi preprostimi tečaji.

Predstavimo še en koncept - zaprta zanka.

Dokažimo izrek: vsaka zaprta zanka je trikrat statično nedoločena.

Za dokaz teorema razmislimo o zaprtem krogu, obremenjenem z zunanjimi silami (slika 8.18).

Izrežemo zaprto konturo z navpičnim prerezom in pokažimo faktorje notranje sile, ki nastanejo na mestu prereza. V vsakem od odsekov se pojavijo trije notranji dejavniki: strižna sila , upogibni moment
in vzdolžna sila
. Skupaj na vsakega od odrezanih delov konture poleg zunanjih sil vpliva šest notranjih dejavnikov (slika 8.18, b, c). Če upoštevamo ravnotežje enega od odrezanih delov, na primer levega (slika 8.18, b), ugotovimo, da je problem trikrat statično nedoločen, saj je za rez mogoče sestaviti samo tri neodvisne ravnotežne enačbe. -off del, na odrezani del pa deluje šest neznanih sil. Tako je stopnja statične nedoločenosti zaprte zanke enaka
. Izrek je dokazan.

Zdaj lahko z uporabo koncepta preprostega tečaja in zaprte zanke oblikujemo še eno pravilo za določanje stopnje statične nedoločenosti:

, (8.5)

kje
 število sklenjenih zank;
 število tečajev glede na enostavne (8,4).

Z enačbo (8.5) določimo stopnjo statične nedoločenosti okvirja, prikazanega na sliki 8.15. Okvir ima pet kontur
, vključno s konturo, ki jo tvorijo podporne palice. Tečaj na vozlišču D je preprost, saj povezuje dve palici. Tečaj v delu K je kompleksen, saj povezuje štiri palice. Število preprostih tečajev, ki bi lahko nadomestili tečaj v odseku K, je po formuli (8.4):
. Tečaj C je tudi zapleten, saj povezuje tri palice. Za ta tečaj
. Poleg tega ima sistem še dva preprosta tečaja, s katerima je pritrjen na podlago. Tako je število preprostih tečajev v sistemu
. Zamenjava števila zaprtih zank
in število preprostih tečajev
v formuli (8.5) določimo stopnjo statične nedoločenosti okvirja:
. Tako je prikazano na sl. 8.15 okvir, sedemkrat statično nedoločen. In to pomeni, da je za izračun takšnega sistema potrebno poleg treh ravnotežnih enačb sestaviti še sedem enačb združljivosti deformacij. Z reševanjem tako dobljenega sistema 10 enačb glede na neznanke, vključene v te enačbe, je mogoče določiti tako velikost reakcij v zunanjih vezeh kot notranje sile, ki nastajajo v okvirju. Postopek reševanja tega problema lahko nekoliko poenostavimo, če iz sistema enačb izločimo ravnotežne enačbe. Vendar ta pristop zahteva uporabo posebnih metod reševanja, med katerimi je tudi metoda sile.

Statično nedoločene sisteme imenujemo sistemi, v katerih notranjih sil ni mogoče določiti samo iz enačb ravnotežja (statične enačbe).

Statično nedoločene konstrukcije imajo t.i odveč povezave. Lahko se pojavijo v nosilcih, palicah in drugih elementih. Takšne povezave se imenujejo "odvečne", ker niso potrebne za zagotavljanje ravnovesja konstrukcije, ampak jih določajo zahteve za njegovo trdnost in togost. Takšne dodatne povezave se imenujejo zunanji. Poleg tega lahko nastanejo nepotrebne povezave zaradi značilnosti same zasnove. Na primer zaprta kontura okvirja (slika 46, G) ima v vsakem odseku tri neznane notranje sile, tj. le šest, od tega trije »ekstra«. Ta dodatni napor se imenuje notranji. Glede na število zunanjih ali notranjih "dodatnih" povezav, ki jih vzpostavijo stopnja statične nedoločenosti sistema. Enako je razliki med številom neznank, ki jih je treba določiti, in številom statičnih enačb. Z eno "dodatno" neznanko se sistem imenuje enkrat ali enkrat statično nedoločen, z dvema - dvakrat statično nedoločen itd.

Zasnova, prikazana na sl. 46, a, je enkrat statično nedoločen in konstrukcije, prikazane na sl. 46, b in v, - dvojno statično nedoločeno, na sl. 46, d - trikrat s statično nedoločeno konstrukcijo.

Pri reševanju statično nedoločenih problemov se poleg statičnih enačb uporabljajo tudi enačbe, ki upoštevajo deformacije konstrukcijskih elementov.

Obstaja več metod za reševanje statično nedoločenih problemov: metoda primerjave pomikov, metoda sile, metoda pomikov.

metoda sile

Pri izračunu statično nedoločenih sistemov sile vzamemo kot neznanke.

Izračun po metoda sile izvajajo v naslednjem zaporedju:

• 1. Nastavite stopnjo statične negotovosti.
• 2. Z odstranitvijo »odvečnih« povezav se prvotni sistem nadomesti s statično determiniranim, t.i. glavni sistem. Lahko se zgradi več takšnih sistemov, pri čemer je treba upoštevati stanje njihove geo

nespremenljivost metrike.

• 3. Glavni sistem je obremenjen z danimi zunanjimi silami in "dodatnimi" neznanimi silami, ki nadomestijo delovanje oddaljenih povezav, kar povzroči enakovreden sistem.
• 4. Za zagotovitev enakovrednosti izvirnega in glavnega sistema je treba neznane sile izbrati tako, da se deformacije glavnega sistema ne razlikujejo od deformacij prvotnega statično nedoločenega sistema. V ta namen se premik točk uporabe "odvečnih" neznank v smeri njihovega delovanja izenači z nič. Iz tako dobljenih dodatnih enačb se določijo vrednosti "dodatnih" neznanih sil. Določanje premikov ustreznih točk je možno na kakršen koli način, vendar je bolje uporabiti najbolj splošno Mohrovo metodo.
• 5. Po določitvi vrednosti "dodatnih" neznanih sil se določijo reakcije in narišejo diagrami notranjih sil, izberejo se odseki in preveri trdnost na običajen način.

Kanonične enačbe metode sil

Dodatne enačbe pomikov, ki izražajo enakost pomikov na nič v smereh "dodatnih" neznank, je mogoče priročno sestaviti v t.i. kanonična oblika tiste. po določenem vzorcu. Pokažimo to na primeru reševanja najenostavnejšega statično nedoločenega sistema (sl. 47, a).

Kot glavni sistem izberemo konzolo, zavržemo zgibno oporo. Ekvivalentni sistem bo dobljen po uporabi njegove zunanje sile T 7 in "ekstra" neznanke X(Slika 47, b).

Kanonična enačba, ki izraža ničelni premik točke AT od sil F in X, bo

Iz enačbe, ki jo imamo

Za sistem, ki ima dve "dodatni" povezavi, ima sistem kanoničnih enačb obliko:

• 8 11 X 1 + b 12 ^2 + ^1
• 621-^1 + 622^2 "I" ^20-

Gibanja A [str In b [y, vključeni v kanonične enačbe, so določeni z Mohrovo metodo.

Za sisteme, sestavljene iz premočrtnih elementov, je priročno izračunati premike po Vereščaginovi metodi.

Na primer, za nalogo, prikazano na sl. 47, z množenjem diagramov (sl. 48), dobimo koeficiente kanonične enačbe:

1 2 I 3 1 I /I 2 1 5 I1 3

E]L LL =-/ / -/ = -, E]A LR =-------- +-------.

1 11 2 3 3 1 1R 2 2 2 2 3 2/ 48 E]

Dobiti Chl - - = - E.

Definiranje moči X, dejansko smo našli odziv podpore Sem za. Nadalje lahko problem določanja notranjih faktorjev sile rešimo, kot običajno, z uporabo metode odsekov.

MINISTRSTVO ZA ŠOLSTVO RUSKE FEDERACIJE

DRŽAVNA INSTITUCIJA

DRŽAVNA TEHNIČNA UNIVERZA KUZBAS

Oddelek za trdnost materialov

IZRAČUN STATIČNO NEDOLOČENIH ZGONSKIH SISTEMOV POD NAPETO - STISKANJEM

Navodila za izvajanje računske in grafične naloge o trdnosti materialov za študente vseh specialnosti

Sestavil: V.D. Moiseenko

Odobreno na seji oddelka, zapisnik št. 8 z dne 29.06.01

Elektronska kopija je v knjižnici glavne stavbe KuzGTU

Kemerovo 2002

Uvod. Obseg in namen naloge

Statično nedoločen sistem tečaj-palica je tisti, pri katerem sil v palicah in reakcij v nosilcih ni mogoče določiti samo iz ravnotežnega pogoja.

Slika 1 prikazuje običajen nosilec, sestavljen iz dveh palic. Sili N 1 in N 2 v palicah tega nosilca je enostavno določiti iz pogoja ravnotežja za sistem konvergentnih sil, ki delujejo na izrezano vozlišče C, saj sta rešeni dve enačbi za ta sistem sil z dvema neznankama.

Če je zasnova nosilca zapletena z dodajanjem še ene palice (slika 1, b), potem sil v palicah ni mogoče določiti na enak način, saj je za vozlišče C še vedno mogoče sestaviti samo dve enačbi statičnega ravnotežja (ΣХ = 0; ΣY = 0), število neznanih sil pa je tri. Enkrat imamo statično nedoločen sistem.

S kompliciranjem zasnove in uvedbo novih palic lahko dobimo statično nedoločen sistem dvakrat (glej sliko 1c), trikrat itd. Zato pod n-krat statično nedoločenim sistemom razumemo tak sistem, v katerem število povezav presega število neodvisnih enačb statike za n enot.

Dodatne enačbe, potrebne za rešitev problema, lahko najdemo z obravnavo sistema v deformiranem stanju in ugotavljanjem povezav med pomiki in deformacijami strukturnih elementov. Nastale enačbe imenujemo enačbe združljivosti deformacij.

Slika 2 prikazuje diagrame nekaterih statično nedoločenih sistemov.

Slika 2. Nekatere vrste statično nedoločenih sistemov

Pri študiju razdelka "Statično nedoločeni palični sistemi" in izvajanju te računske in grafične naloge mora študent spoznati značilnosti statično nedoločenih sistemov; osvojijo veščine razkrivanja statične nedoločenosti, določanja sil v konstrukcijskih elementih in izbire prečnih površin iz trdnostnega pogoja.

Naloga od študenta zahteva, da naredi naslednje:

- določiti sile v palicah in izbrati površine preseka od delovanja zunanjih obremenitev;

- določi dodatne napetosti v palicah zaradi temperaturnih sprememb;

- določite dodatne pritrdilne napetosti, ki jih povzroči netočnost pri izdelavi palic;

- izberite odseke palic glede na mejno stanje.

Obseg in oblika izvajanja računske in grafične naloge sta odvisna od obsega predmeta, ki se preučuje, in ju učitelj pogaja pri praktičnem pouku.

1. Kratke teoretične informacije

Pri reševanju statično nedoločenih problemov je treba upoštevati naslednji vrstni red:

1.1. Razmislite o statični strani problema. Sestavite načrt sil in zapišite enačbe statike.

1.2. Razmislite o geometrijski plati problema. Sestavite načrt potovanja. Sestavite dodatne enačbe združljivosti deformacij v taki količini, da je mogoče najti vse neznane sile.

1.3. Razmislite o fizični plati problema. Po fizikalnih zakonih (z izračunom temperature) in po Hookovem zakonu izrazite deformacije v enačbah njihove združljivosti z neznanimi silami, ki delujejo v palicah:

1.4. Izdelajte skupno rešitev enačb statike, geometrije, fizike in določite neznane sile.

1.5. Uporaba pogojev tlačne ali natezne trdnosti N/F = [ σ ], izberite površine preseka palic.

1.6. Z znanimi silami v palicah in sprejetimi površinami preseka izračunajte normalne napetosti po formuli

σ = N F .

2. Primer

Podano: Absolutno tog nosilec AB počiva, kot je prikazano na sliki 3, obremenjen z enakomerno porazdeljeno obremenitvijo in silo P.

Slika 3. Diagram statično nedoločenega sistema

Začetni podatki za izračun

4. Določite skupne napetosti v palicah zaradi delovanja obremenitev, temperaturnih sprememb in proizvodnih netočnosti.

2.1. Izračun statično nedoločenega zgibnega paličnega sistema za zunanjo obremenitev

P = 30 kN q = 15 kN/m

A C B

Slika 4. Začetna načrtovalna shema

2.1.1. Statična stran problema

Statično stran problema obravnava načrt sil. Načrt sil je konstrukcijska shema, ki prikazuje vse sile (tako znane kot neznane), ki delujejo na element sistema zgibne palice, katerega ravnotežje je upoštevano (v našem primeru je to togi nosilec AB). Prerežemo jeklene in bakrene palice in nadomestimo njihove odpadne spodnje dele z notranjimi silami (slika 5).

P = 30 kN q = 15 kN/m

A C B

60°

riž. 5. Načrt sil zunanjih obremenitev

Iz načrta sil (glej sliko 5) zapišemo enačbe statičnega ravnovesja. Za odgovor na prvo vprašanje naloge je treba poznati sile v palicah - jekleni in bakreni. V tem primeru ni treba izračunati reakcije zgibne podpore. Torej od treh

možne enačbe statike (ΣX = 0; ΣY = 0 ; Σm c = 0) zapišemo

tisti, ki ne vključuje reakcij vrtljivo pritrjene podpore C:

∑ mC = 0

− N CT a + q a 2 2 + p a + NM sin60o b = 0,

− N ST 2 + 15 2 2 2 + 30 2 − NM 0,866 4 = 0,

Po algebraičnih operacijah bo ravnotežna enačba dobila obliko

2.1.2. Geometrična stran problema

Geometrična plat problema je obravnavana s premičnim načrtom. Načrt premikov je konstrukcijski diagram, ki prikazuje položaj sistema zgibne palice pred in po obremenitvi. Na načrtu pomikov označimo pomike točk žarka (AA1 in BB1),

absolutne deformacije bakrenih in jeklenih palic (∆ l ST ; ∆ l M )

(slika 6). Poleg tega zaradi majhnih deformacij premikamo konice žarka navpično navzgor ali navzdol, deformacije nagnjenih palic pa označimo s pravokotno.

riž. 6. Načrt pomikov od delovanja zunanjih obremenitev

Po načrtu pomikov sestavimo enačbo za združljivost deformacij. Najprej zapišemo razmerje pomikov točk žarka iz podobnosti trikotnikov AA1 C in CBB1 (slika 6):

Premiki točk nosilca (AA1 in BB1) so izraženi z deformacijami

Izraza (2.3) in (2.4) nadomestimo v relacijo (2.2):

2.1.3. Fizična stran problema

Dobljene enačbe združljivosti deformacij (2.5) v tej obliki ni mogoče rešiti z ravnotežno enačbo (2.1), ker so neznane količine, ki so v njih vključene, drugačne narave.

Absolutni deformaciji ∆ l CT in ∆ l M v enačbi (2.5) izrazimo

Dobili smo enačbo združljivosti deformacij, zapisano v terminih sil v palicah.

2.1.4. Sinteza

Skupaj rešimo enačbe ravnotežja (2.1) in enačbo združljivosti deformacij (2.6).

NCT + 1,73 NM = 45

0,67 NCT \u003d 0,95 NM.

Iz druge enačbe sistema izrazimo silo N ST:

in nadomestimo v prvo enačbo sistema.

Pozitiven rezultat N ST in N M potrjuje naše predpostavke o stiskanju jeklene palice in napetosti bakrene palice, kar pomeni, da bodo sile v palicah:

2.1.5. Izbira prerezov palic

Izbira prerezov palic se izvede glede na pogoj natezne trdnosti - stiskanje:

N F ≤ [σ] .

a) Prečni prerez jeklene palice, ki se zahteva glede na pogoj trdnosti, bo določen:

b) Prečni prerez bakrene palice, ki se zahteva glede na trdnost, bo določen:

V tem primeru mora biti glede na dano razmerje površin površina jeklene palice enaka:

FCT = 4 3 FM = 4 3 1,7 10- 4 = 1,275 10- 4 m2 ..

Sprejemamo velike preseke palic:

S sprejetimi površinami preseka bakrenih in jeklenih palic določimo napetosti v teh palicah.

2.2. Temperaturni izračun statično nedoločenega sistema zgib-palica

Namen temperaturnega izračuna je določiti dodatne napetosti v bakrenih in jeklenih palicah zaradi temperaturnih sprememb.

Recimo, da se sistem segreje za ∆ t = 20 o C . Algoritem rešitve ostaja enak. Začetna konstrukcijska shema je prikazana na sl. 7.

Imenujejo se palični sistemi, pri katerih podpornih reakcij in faktorjev notranjih sil ni mogoče najti samo iz enačb ravnotežja statično nedoločen.

Razlika med številom zahtevanih neznanih sil in neodvisnimi ravnotežnimi enačbami določa stopnja statične nedoločenosti sistema. Stopnja statične nedoločenosti je vedno enaka številu redundantnih (odvečnih) povezav, katerih odstranitev spremeni statično nedoločen sistem v statično določljiv geometrijsko nespremenljiv sistem. Odvečne so lahko tako zunanje (referenčne) povezave kot notranje, ki nalagajo določene omejitve gibanja sistemskih odsekov relativno drug proti drugemu.

Geometrijsko nespremenljiv imenujemo tak sistem, katerega sprememba oblike je možna le v povezavi z deformacijami njegovih elementov.

Geometrijsko spremenljiv imenujemo tak sistem, katerega elementi se lahko premikajo pod vplivom zunanjih sil brez deformacije (mehanizem).

Prikazano na sl. 12.1 okvir ima sedem zunanjih (podpornih) povezav. Za določitev sil v teh vezeh (opornih reakcij) je mogoče sestaviti samo tri neodvisne ravnotežne enačbe. Zato ima ta sistem štiri redundantne povezave, kar pomeni, da je štirikrat statično nedoločen. Tako je stopnja statične negotovosti za ravne okvirje:

kje R- število odzivov podpore.

Kontura, sestavljena iz številnih elementov (ravnih ali krivuljnih), togo (brez tečajev), povezanih med seboj in tvorijo zaprt krog, se imenuje zaprt krog. . Pravokotni okvir, prikazan na sliki 12.2, je zaprta zanka. Je trikrat statično nedoločen, saj je za njegovo statično nedoločenost treba odrezati enega od njegovih elementov in odstraniti tri dodatne povezave. Reakcije teh vezi so: vzdolžna sila, prečna sila in upogibni moment, ki delujejo na mestu reza; jih ni mogoče določiti z enačbami statike. V podobnih pogojih, v smislu statične nedoločenosti, obstaja katera koli zaprta zanka, ki je vedno trikrat statično nedoločen.

Vključitev tečaja v vozlišče okvirja, v katerem se zbližata dve palici, ali postavitev na poljubno mesto na osi palice odstrani eno povezavo in zmanjša skupno stopnjo statične nedoločenosti za eno. Tak tečaj se imenuje enojni ali preprost (slika 12.3).

Na splošno je vsak tečaj vključen v povezovalno vozlišče c palice, zmanjša stopnjo statične negotovosti za c-1 , saj tak tečaj zamenja c-1 enojni tečaji (slika 12.3). Tako je stopnja statične nedoločenosti sistema v prisotnosti zaprtih zank določena s formulo.

Takšen sistem imenujemo statično nedoločen, če ga ni mogoče izračunati samo z enačbami statike, saj ima nepotrebne povezave. Za izračun takih sistemov se sestavijo dodatne enačbe, ki upoštevajo deformacije sistema.

Statično nedoločeni sistemi imajo številne značilne lastnosti:

1. statično nedoločen strukture so bolj toge od ustreznih statično določena, saj imajo dodatne povezave.
2. V statično nedoločen sistemov so notranje sile manjše, kar določa njihovo učinkovitost v primerjavi z statično določena sistemov pod enakimi zunanjimi obremenitvami.
3. Kršitev nepotrebnih povezav v statično nedoločen sistem ne vodi vedno v uničenje, medtem ko izguba komunikacije v statično določena sistem ga naredi geometrijsko spremenljivega.
4. Za izračun statično nedoločen sistemov, je potrebno predhodno določiti geometrijske značilnosti prerezov elementov, tj. pravzaprav njihova oblika in velikost, saj njihova sprememba povzroči spremembo sil v povezavah in novo porazdelitev naporov v vseh elementih sistema.
5. Pri izračunu statično nedoločen sistemov, je treba material izdelave izbrati vnaprej, saj je treba poznati njegove module elastičnosti.
6. V statično nedoločen sistemov, temperaturni vplivi, posedanje nosilcev, netočnosti pri izdelavi in ​​montaži povzročajo dodatne napore.

Glavni metode izračunastatično nedoločen sistemi so:

1. metoda sile. Tu so sile obravnavane kot neznanke - sile in momenti.
2.Metoda gibanja. Neznani so dejavniki deformacije - koti vrtenja in linearni pomiki.
3.mešana metoda. Pri tem del neznank predstavlja napore, drugi del pa premike.
4. Kombinirana metoda. Uporablja se pri izračunu simetričnih sistemov za nesimetrične obremenitve. Izkazalo se je, da je sistem za simetrično komponento dane obremenitve priporočljivo izračunati z metodo premika, za obratno simetrično komponento pa z metodo sile.
Poleg navedenih analiznih metod se pri izračunu posebej kompleksnih sistemov uporabljajo različne numerične metode.

Kanonične enačbe metode sil

Za pridobitev dodatnih enačb, ki smo jih omenili v prejšnjem odstavku, morate dano najprej n-krat obrniti statično nedoločen sistem v statično determiniran tako, da iz njega odstranimo nepotrebne povezave. Nastali statično določen sistem se imenuje osnovni. Upoštevajte, da transformacija danega sistema v statično določenega ni obvezna. Včasih se uporabi modifikacija metode sile, v kateri je lahko osnovni sistem statično nedoločen vendar pa predstavitev tega vprašanja presega obseg tega priročnika. Izločitev morebitnih vezi ne spremeni notranjih sil in deformacij sistema, če nanj delujejo dodatne sile in momenti, ki so reakcije zavrženih vezi. To pomeni, da če se dana obremenitev in reakcije oddaljenih povezav uporabijo za glavni sistem, bosta glavni in dani sistem postala enakovreden.

V danem sistemu ne more biti premikov vzdolž smeri obstoječih togih členov, vključno s tistimi členi, ki se pri prehodu v glavni sistem zavržejo, zato morajo v glavnem sistemu premiki vzdolž smeri zavrženih členov biti enak nič. In za to morajo imeti reakcije padlih vezi strogo določene vrednosti.

Pogoj enakosti ničelnemu pomiku v smeri katere koli i-te povezave od n zavrženih na podlagi načela neodvisnosti delovanja sil ima obliko:

kjer prvi indeks označuje smer gibanja in številko odpadle povezave, drugi pa razlog, ki je povzročil premik, tj. je premik v smeri i-te vezi, ki ga povzroči reakcija k-te vezi; - premikanje v smeri i-te povezave, ki ga povzroča hkratno delovanje celotne zunanje obremenitve.

Pri metodi sil je reakcija k-te vezi običajno označena z Xk. Ob upoštevanju te oznake in zaradi veljavnosti Hookovega zakona lahko premike predstavimo kot:

kjer je eno (ali specifično) gibanje v smeri i-te vezi, ki ga povzroči reakcija, tj. reakcija, ki sovpada v smeri z Xk, vendar enaka enoti.

Če nadomestimo (2) v (1), dobimo:

fizični pomen enačba (3): premik v glavnem sistemu v smeri i-te zavržene povezave je enak nič.

Če zapišemo izraze, podobne (3), za celotno množico zavrženih vezi, dobimo sistem kanoničnih enačbmetoda sile:

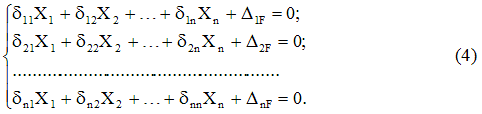
Oblika enačbe (4), tj. število izrazov v vsakem od njih in njihovo skupno število je določeno le s stopnjo statične nedoločenosti sistema in ni odvisno od njegovih posebnih lastnosti.

Koeficiente sistema kanoničnih enačb (4) določimo po Mohr-Vereshchaginovi metodi z množenjem ustreznih diagramov. Vsi ti koeficienti, kot je navedeno zgoraj, predstavljajo premike; koeficienti, ki stojijo pri neznankah, so enotski premiki, prosti členi pa so tovor. Posamezni gibi so razdeljeni na glavni, ki se nahajajo vzdolž glavne diagonale in imajo enake indekse in stranski učinki(). Večji premiki so vedno pozitivni, za razliko od stranskih. Simetrično locirani premiki so v skladu z izrekom o vzajemnosti premikov med seboj enaki, tj. .

Algoritem za izračun metode sile

Ne glede na značilnosti obravnavane zasnove je mogoče razlikovati naslednje zaporedje izračuna statično nedoločenih sistemov metoda sile:

1. Določite stopnjo statične negotovosti.
2. Izberite glavni sistem.
3. Oblikujte enakovredni sistem.
4. Zažgite sistem kanonične enačbe.
5. Izdelajte diagrame enot in obremenitev faktorjev notranje sile, ki nastanejo v elementih obravnavane konstrukcije.
6. Izračunajte koeficiente neznank in proste člene sistema kanoničnih enačb.
7. Zgradite skupni enojni diagram.
8. Izvedite univerzalno preverjanje koeficientov za neznane in proste člene.
9. Reši sistem (4), tj. določite reakcije dodatnih vezi.
10. Izdelajte diagrame nastajajočih notranjih faktorjev sile za dani sistem (z drugimi besedami končne diagrame).
11. Izvedite statična in kinematična preverjanja.
Upoštevajte, da točke 7, 8, 11 zgornjega algoritma niso nujno potrebne, čeprav vam omogočajo nadzor nad pravilnostjo izračuna. In za sisteme z eno dodatno povezavo sta točki 7 in 8 preprosto brez pomena, saj v tem primeru skupni enojni diagram sovpada z enim.
Oglejmo si podrobneje nekaj zgornjih korakov izračuna.

Izbira primarnega sistema

To je najpomembnejša faza izračuna, saj racionalna izbira glavnega sistema močno poenostavi računsko delo. Razmislimo o možnih načinih za odstranitev nepotrebnih povezav, ki določajo obliko glavnega sistema.

1. Zavrnitev nepotrebnih povezav se izvede s popolno odstranitvijo nekaterih podpor ali njihovo zamenjavo s podporami z manjšim številom povezav. Reakcije, ki delujejo v smeri spuščenih vezi, so redundantne neznanke. Slika 1, b, c, d prikazuje različne različice ekvivalentnega sistema, pridobljenega s to metodo za okvir (slika 1, a).

2. Postavitev tečajev v vmesnih odsekih palic omogoča v vsakem takem odseku vzpostavitev povezave, ki ustreza upogibnemu momentu. Ti trenutki so odvečne neznanke. Za okvir s stopnjo statične nedoločenosti n = 3 (slika 2, a) je treba pri izbiri glavnega sistema namestiti tri tečaje. Položaj teh tečajev je lahko poljuben, vendar izpolnjuje zahtevo geometrijske nespremenljivosti sistema (slika 2b).

3. Razrez palice odpravi tri vezi, ki ustrezajo notranjim silam M, Q, N (slika 2, c). V posebnih primerih (slika 2d) rezanje palice vzdolž tečaja sprosti dve vezi (slika 2, e), rezanje ravne palice s tečaji na koncih pa sprosti eno vez (slika 2, f).

Med povezavami statično nedoločenega sistema ločimo absolutno potrebne in pogojno potrebne. Nujno potrebne so povezave, po odstranitvi katerih sistem postane geometrijsko spremenljiv. Za absolutno nujno povezavo je značilna statična določljivost napora v njej, tj. reakcijo take vezi lahko izračunamo iz ravnotežnega pogoja. Pri izbiri glavnega sistema ni mogoče zavreči nujno potrebnih povezav.

Odnosi, po odstranitvi katerih sistem ostane geometrijsko nespremenjen, se imenujejo pogojno potrebni. Sistem, ki ni bil povezan, je lahko primarni sistem metoda sile.

Izračun koeficientov in prostih členov kanoničnih enačb

Pred to fazo izračuna je izdelava diagramov enote in obremenitve notranjih faktorjev sile (za nosilce in okvirje - diagrami upogibnih momentov). Enotski diagrami so zgrajeni iz delovanja brezdimenzionalne enotske sile ali brezdimenzionalnega enotskega momenta, ki sovpada v smeri s smerjo ustreznega presežka, neznanega v ekvivalentnem sistemu, in so označeni z , enotski diagram pa z .

Diagram obremenitve je sestavljen iz zunanje obremenitve, ki se nanaša na glavni sistem. V tem primeru lahko sestavite en diagram iz hkratnega delovanja vseh zunanjih obremenitev ali več diagramov, ločeno od vsake uporabljene obremenitve. Takšna razdelitev enega obremenitvenega diagrama na več enostavnejših je praviloma priporočljiva le, če je med obstoječimi obremenitvami ena enakomerno porazdeljena in je momentni diagram v ustreznem odseku pod njim izmenično predznačen. V tem primeru bo v vsaki kanonični enačbi število prostih členov enako številu izrisanih obremenitvenih diagramov.

Premike enot in obremenitev (koeficiente in proste člene kanoničnih enačb) je mogoče na splošno izračunati po Mohrovi metodi. Za tramove in okvirje je to mogoče storiti z uporabo Vereshchaginovega pravila.

Univerzalno preverjanje koeficientov in prostih členov kanoničnih enačb

Za izvedbo univerzalnega preverjanja je treba zgraditi skupni diagram enote - diagram trenutkov iz hkratnega delovanja vseh sil enote, ki delujejo na glavni sistem:

Skupni enojni diagram pomnožimo z diagramom:

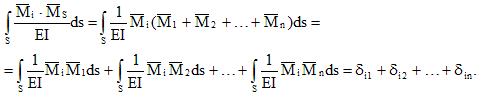
Tako je rezultat množenja celotnega in i-tega posameznega diagrama premik v smeri i-te povezave iz skupnega delovanja posameznih dodatnih neznank. Ta premik je enak vsoti koeficientov i-te kanonične enačbe:

To preverjanje se imenuje vrstico za vrstico in velja za vsako kanonično enačbo.
Namesto n preverjanj vrstic se najpogosteje izvaja ena - univerzalni pregled, ki je sestavljen iz množenja skupnega diagrama enote samega in preverjanja pogoja:

Če je opravljeno univerzalno preverjanje, so premiki enot izračunani pravilno; če ne, je treba opraviti preglede po vrsticah, kar vam bo omogočilo razjasnitev premika, pri izračunu katerega je prišlo do napake.

Za preverjanje premikov obremenitve je potrebno pomnožiti skupno enoto in diagrame obremenitve upogibnih momentov:

Tako je preverjanje prostih členov sistema kanoničnih enačb (4) sestavljeno iz izpolnjevanja pogoja.