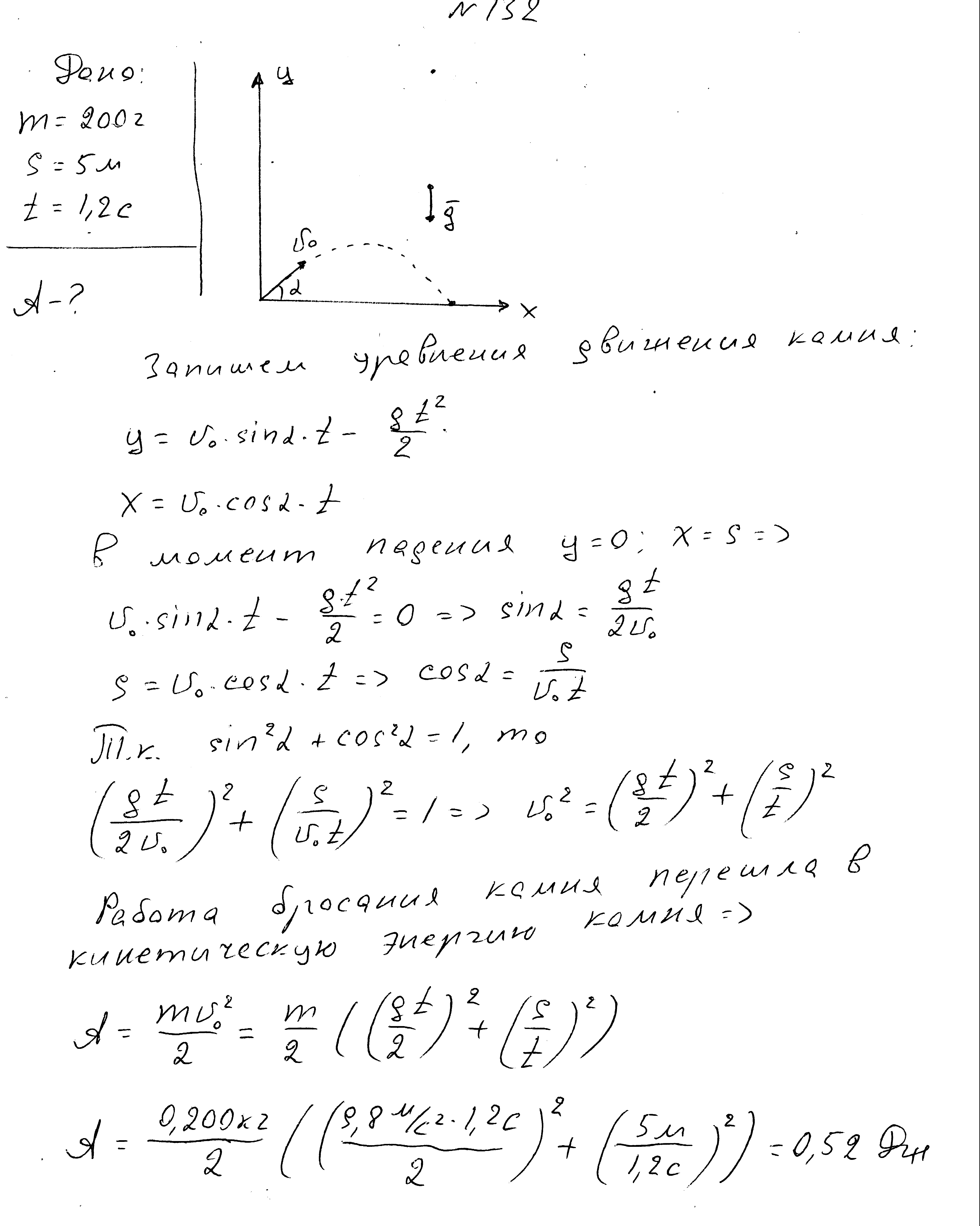Preučevanje gibanja telesa, vrženega pod kotom na vodoravno ravnino. Gibanje telesa, vrženega pod kotom na obzorje! Fizika: gibanje telesa, vrženega pod kotom na vodoravno ravnino

Če telo vržemo pod kotom na obzorje, potem med letom nanj delujeta sila težnosti in sila zračnega upora. Če zanemarimo silo upora, je edina preostala sila gravitacija. Zato se zaradi 2. Newtonovega zakona telo giblje s pospeškom, ki je enak težnemu pospešku; projekcije pospeška na koordinatne osi ax = 0, ay = - g.

Slika 1. Kinematične značilnosti telesa, vrženega pod kotom na horizontalo

Vsako kompleksno gibanje materialne točke je mogoče predstaviti kot superpozicijo neodvisnih gibanj vzdolž koordinatnih osi, v smeri različnih osi pa se lahko vrsta gibanja razlikuje. V našem primeru lahko gibanje letečega telesa predstavimo kot superpozicijo dveh neodvisnih gibanj: enakomernega gibanja vzdolž vodoravne osi (os X) in enakomerno pospešenega gibanja vzdolž navpične osi (os Y) (slika 1). .

Projekcije hitrosti telesa se torej spreminjajo s časom na naslednji način:

kjer je $v_0$ začetna hitrost, $(\mathbf \alpha )$ je vrzni kot.

Z našo izbiro izvora so začetne koordinate (slika 1) $x_0=y_0=0$. Potem dobimo:

(1)

Analizirajmo formule (1). Določimo čas gibanja vrženega telesa. Če želite to narediti, nastavimo koordinato y enako nič, ker v trenutku pristanka je višina telesa nič. Od tu dobimo čas letenja:

Druga časovna vrednost, pri kateri je višina enaka nič, je nič, kar ustreza trenutku metanja, tj. ta vrednost ima tudi fizični pomen.

Domet letenja dobimo iz prve formule (1). Domet leta je vrednost koordinate x na koncu leta, tj. v času, ki je enak $t_0$. Če nadomestimo vrednost (2) v prvo formulo (1), dobimo:

Iz te formule je razvidno, da je največji doseg letenja dosežen pri vržnem kotu 45 stopinj.

Največjo višino dviga vrženega telesa lahko dobimo iz druge formule (1). Če želite to narediti, morate v to formulo nadomestiti časovno vrednost, ki je enaka polovici časa letenja (2), ker Največja višina leta je na sredini poti. Izvajanje izračunov, dobimo

Iz enačb (1) lahko dobimo enačbo trajektorije telesa, tj. enačba, ki povezuje x in y koordinate telesa med gibanjem. Če želite to narediti, morate izraziti čas iz prve enačbe (1):

in ga nadomestite v drugo enačbo. Potem dobimo:

Ta enačba je enačba trajektorije gibanja. Vidimo lahko, da je to enačba parabole z vejami navzdol, kot je označeno z znakom »-« pred kvadratnim členom. Upoštevati je treba, da so vrzni kot $\alpha $ in njegove funkcije tukaj preprosto konstante, tj. stalna števila.

Telo vržemo s hitrostjo v0 pod kotom $(\mathbf \alpha )$ glede na vodoravno ravnino. Čas letenja $t = 2 s$. Do katere višine Hmax se bo dvignilo telo?

$$t_B = 2 s$$ $$H_max - ?$$

Zakon gibanja telesa ima obliko:

$$\levo\( \begin(matrika)(c) x=v_(0x)t \\ y=v_(0y)t-\frac(gt^2)(2) \end(matrika) \desno.$ $

Vektor začetne hitrosti tvori kot $(\mathbf \alpha )$ z osjo OX. torej

\ \ \

Kamen je vržen z vrha gore pod kotom = 30$()^\circ$ proti obzorju z začetno hitrostjo $v_0 = 6 m/s$. Kot nagnjene ravnine = 30$()^\circ$. Kako daleč od mesta metanja bo kamen pristal?

$$ \alpha =30()^\circ$$ $$v_0=6\ m/s$$ $$S - ?$$

Izhodišče koordinat postavimo na točko meta, OX - vzdolž nagnjene ravnine navzdol, OY - pravokotno na nagnjeno ravnino navzgor. Kinematične značilnosti gibanja:

Zakon gibanja:

$$\levo\( \begin(array)(c) x=v_0t(cos 2\alpha +g\frac(t^2)(2)(sin \alpha \ )\ ) \\ y=v_0t(sin 2 \alpha \ )-\frac(gt^2)(2)(cos \alpha \ ) \end(matrika) \desno.$$ \

Če nadomestimo dobljeno vrednost $t_В$, najdemo $S$:

Še 3 sekunde je bilo do konca finalne tekme košarkarskega turnirja Olimpijskih iger 1972 v Münchnu. Američani - reprezentanca ZDA - so že proslavljali zmago! Naša ekipa - reprezentanca ZSSR - je zmagala s približno 10 točkami razlike proti veliki Dream Team...

Nekaj ​​minut pred koncem tekme. Toda, ko je na koncu izgubila vso prednost, je že izgubljala točko 49:50. Potem se je zgodilo neverjetno! Ivan Edeshko vrže žogo izza končne črte čez celotno igrišče pod ameriškim ringom, kjer naš center Alexander Belov sprejme žogo, obkrožen z dvema nasprotnikoma, in jo položi v koš. 51:50 – olimpijski prvaki smo!!!

Kot otrok sem takrat doživljal najmočnejša čustva - najprej razočaranje in užaljenost, potem pa noro veselje! Čustveni spomin na to epizodo se je vtisnil v mojo zavest za vse življenje! Oglejte si video na internetu na zahtevo "Zlati met Aleksandra Belova", ne bo vam žal.

Američani nato niso priznali poraza in zavrnili prejem srebrnih medalj. Je mogoče v treh sekundah narediti to, kar so naši igralci? Spomnimo se fizike!

V članku si bomo ogledali gibanje telesa, vrženega pod kotom na obzorje, izdelali program v Excelu za reševanje tega problema z različnimi kombinacijami vhodnih podatkov in poskušali odgovoriti na zgoraj zastavljeno vprašanje.

To je precej znan problem v fiziki. V našem primeru je telo, vrženo pod kotom na vodoravno, košarkarska žoga. Izračunali bomo začetno hitrost, čas in pot žoge, ki jo je čez celotno igrišče vrgel Ivan Edeshko in padla v roke Aleksandra Belova.

Matematika in fizika košarkarskega leta.

Spodaj predstavljene formule in izračuni soexcel so univerzalni za širok spekter problemov o telesih, vrženih pod kotom na obzorje in letečih po parabolični tirnici brez upoštevanja vpliva zračnega trenja.

Diagram izračuna je prikazan na spodnji sliki. Zaženite MS Excel ali OOo Calc.

Začetni podatki:

1. Ker smo na planetu Zemlja in razmišljamo o balističnem problemu - gibanju teles v gravitacijskem polju Zemlje, bomo najprej zapisali glavno karakteristiko gravitacijskega polja - pospešek prostega pada. g v m/s 2

v celico D3: 9,81

2. Dimenzije košarkarskega igrišča so 28 metrov v dolžino in 15 metrov v širino. Vodoravna razdalja žoge od skoraj celotnega igrišča do obroča od nasprotne osnovne črte x napiši v metrih

v celico D4: 27,000

3. Če predpostavimo, da je Edeshko izvedel met z višine približno dveh metrov, Belov pa je žogo ujel nekje na ravni obroča, potem je pri košarkarskem obroču višine 3,05 metra navpična razdalja med točkama odhoda in prihoda žoge bo 1 meter. Zapišimo navpični pomik l v metrih

v celico D5: 1,000

4. Kot izstrelitve žoge po mojih meritvah na video posnetku α 0 od Edeshkovih rok ni presegla 20°. Vnesemo to vrednost

v celico D6: 20,000

Rezultati izračuna:

Osnovne enačbe, ki opisujejo gibanje telesa, vrženega pod kotom na obzorje, brez upoštevanja zračnega upora:

x =v 0*cos α 0 *t

l =v 0*greh α 0 *t -g *t 2 /2

5. Izrazimo čas t iz prve enačbe, jo nadomestite z drugo in izračunajte začetno hitrost žogice v 0 v m/s

v celici D8: =(D3*D4^2/2/COS (RADIAN(D6))^2/(D4*TAN (RADIAN(D6)) -D5))^0,5 =21,418

v 0 =(g *x 2 /(2*(cosα 0 ) 2 *(x *tgα 0 -y )) 0,5

6. Čas letenja žoge iz rok Edeshka v roke Belova t Izračunajmo v sekundah, saj vemo zdaj v 0 , iz prve enačbe

v celici D9: =D4/D8/COS (RADIAN(D6)) =1,342

t = x /(v 0 * cosα 0 )

7. Poiščimo smerni kot hitrosti leta žogice α jaz na točki trajektorije, ki nas zanima. Da bi to naredili, zapišemo začetni par enačb v naslednji obliki:

l =x *tgα 0 -g *x 2 /(2*v 0 2*(kerα 0 ) 2)

To je enačba parabole – poti leta.

Najti moramo kot naklona tangente na parabolo na točki, ki nas zanima - to bo kot α jaz. Če želite to narediti, vzemite odvod, ki je tangens tangentnega kota:

y' =tgα 0 -g *x /(v 0 2*(kerα 0 ) 2)

Izračunajmo kot prihoda žoge v roke Belova α jaz v stopinjah

v celici D10: =ATAN (TAN (RADIANS(D6)) -D3*D4/D8^2/COS (RADIANS(D6))^2)/PI()*180 =-16,167

α jaz = arctgl ’ = arctg(tgα 0 — g * x /(v 0 2 *(cosα 0 ) 2))

Izračun v Excelu je v bistvu končan.

Druge možnosti plačila:

Z napisanim programom lahko hitro in enostavno izvedete izračune z drugimi kombinacijami začetnih podatkov.

Naj je dana vodoravna x = 27 metrov , navpično l = 1 meter dometa letenja in začetne hitrosti v 0 = 25 m/s.

Moramo najti čas leta t in odhodni koti α 0 in prihod α jaz

Uporabimo storitev MS Excel “Izbira parametrov”. V več člankih na blogu sem že večkrat podrobno razložil, kako ga uporabljati. Več o uporabi te storitve lahko preberete.

Vrednost v celici D8 nastavimo na 25.000 tako, da vrednost v celici D6 spremenimo z izbiro. Rezultat je na spodnji sliki.

Izvorni podatki so v tej različici izračuna v Excelu (tako kot v prejšnji) označeni z modrimi okvirji, rezultati pa obrobljeni z rdečimi pravokotnimi okvirji!

Nastavitev v tabeliExcel nekaj zanimive vrednosti v eni od celic s svetlo rumenim polnilom, če izberete spremenjeno vrednost v eni od celic s svetlo turkiznim polnilom, lahko na splošno dobite deset različnih možnosti za rešitev problema gibanja telesa, vrženega na kota do obzorja za deset različnih kompletov izvirnih podatkov!!!

Odgovor na vprašanje:

Odgovorimo na vprašanje, zastavljeno na začetku članka. Žoga, ki jo je poslal Ivan Edeshko, je po naših izračunih Belovu priletela v 1,342 sekunde. Alexander Belov je ujel žogo, pristal, skočil in vrgel. Za vse to je imel veliko časa – 1,658 sekunde! To je res dovolj časa! Podroben pregled video posnetkov potrjuje navedeno. Naši igralci so imeli na voljo tri sekunde, da so žogo od svoje končne črte podali do nasprotnikove table in jo vrgli v obroč ter se tako z zlatom zapisali v zgodovino košarke!

prosim spoštljivo avtorsko delo prenesi datoteko po naročnini za objave člankov!

Prosti pad predstavlja poseben primer enakomerno pospešenega gibanja brez začetne hitrosti. Pospešek tega gibanja je enak gravitacijskemu pospešku, imenovan tudi gravitacijski pospešek. Za to gibanje veljajo formule:

u t
g
h- višina, s katere telo pade
t- čas, v katerem se je padec nadaljeval

Opomba:

• Zračni upor v teh formulah ni upoštevan.
• Gravitacijski pospešek ima dano vrednost (9,81 (m/s?)) blizu zemeljske površine. Vrednost g se spreminja tudi na drugih razdaljah od zemeljske površine!

Gibanje telesa, vrženega navpično navzgor

Telo, vrženo navpično navzgor, se giblje enakomerno počasi z začetno hitrostjo u0 in pospeševanje a = -g. Gibanje telesa skozi čas t predstavlja višino dviga h.Za to gibanje veljajo naslednje formule:

U0- začetna hitrost gibanja telesa
U- hitrost, s katero telo pade po določenem času t
g- pospešek prostega pada, 9,81 (m/s?)
h- višina, do katere se bo telo čez čas dvignilo t
t- čas

Hitrost telesa na določeni višini:

Največja višina dviga:

Čas za dvig na največjo višino:

Dodajanje gibov, usmerjenih pod kotom drug na drugega.

Telo lahko hkrati sodeluje v več translacijskih gibih. Ker so pospešek, hitrost in premik vektorske količine, jih lahko seštevamo po zakonih vektorskega (geometričnega) seštevanja. Tisti. po pravilu paralelograma.

Izračuna se lahko končna vrednost katere koli karakteristike gibanja.

če:
Gor- nastala trenutna hitrost,
U1- trenutna hitrost prvega premika,
U2- trenutna hitrost drugega gibanja,
? - kot, ki ga tvorita vektorja hitrosti u1 in u2,
Nato z uporabo kosinusnega izreka dobimo:

Če se premiki 1 in 2 zgodita pravokotno drug na drugega, potem je formula poenostavljena, ker

Gibanje telesa, vrženega vodoravno.

Gibanje vodoravno vrženega telesa je kombinacija dveh medsebojno pravokotnih gibanj:
- horizontalno (enakomerno) gibanje,
- navpično (prosti pad)

Enačba poti vodoravno vrženega telesa

Če sestavimo trajektorijo vodoravno vrženega telesa v koordinatnem sistemu xy, pri čemer je točka izmeta kot izhodišče koordinat, smer ordinatne osi pa sovpada s smerjo vektorja pospeška prostega pada, potem koordinate vsake točke trajektorije predstavljajo gibanje telesa v vodoravni smeri (gibanje s konstantno hitrostjo U0) in v navpični smeri (enakomerno pospešeno gibanje s pospeškom g)

x, y- telesne koordinate,
u0
g
t- čas potovanja (s)

Enačba poti vodoravno vrženega telesa kot sledi:

g in začetno hitrost telesa u0 so konstantne količine, potem koordinata l sorazmerno s kvadratom x, tj. tir gibanja je parabola, katere vrh je v začetni točki gibanja.

Položaj vektorja vodoravno vrženega telesa, formula

Položaj vsake točke trajektorije vodoravno vrženega telesa je mogoče določiti z vektorjem položaja r, ki predstavlja nastali premik:

oz Vektor položaja:

x-koordinata:

Y-koordinata:

Opomba: Zračni upor v formulah ni upoštevan.

Enačba gibanja telesa, vrženega pod kotom na vodoravno ravnino.

Koordinate točke trajektorije opisujejo enačbe:

x, y- telesne koordinate
U0- začetna hitrost telesa (m/s)
? - kot, pod katerim je telo vrženo proti obzorju (°)
g- pospešek prostega pada 9,81 (m/s2)
t- čas potovanja (s)

Iz formul preko parametra t izpeljemo splošno enačba gibanja telesa, vrženega pod kotom na vodoravno ravnino

Od gravitacijskega pospeška g, ? - kot, pod katerim je telo vrženo proti obzorju, in začetna hitrost telesa u0 so konstantne količine, potem koordinata l sorazmerno s kvadratom x, tj. trajektorija gibanja je parabola, začetna točka je na eni od njenih vej, vrh parabole pa je točka največjega dviga telesa.

Čas dviga do največje višine telesa, vrženega pod kotom na obzorje.

Čas dviga na največjo višino se določi iz pogoja, da je navpična komponenta trenutne hitrosti enaka nič

iz te enačbe dobimo:

U0- začetna hitrost telesa (m/s),
?
g- pospešek prostega pada 9,81 (m/s2),
thmax- čas dviga na največjo višino (s)

Vrzna razdalja telesa, vrženega pod kotom na vodoravno ravnino.

Razpon meta oz radij poškodbe določen s formulama za skupni čas gibanja in formulo za telesne koordinate

nadomeščanje tsmax v izraz in poenostavitev dobimo:

U0- začetna hitrost telesa (m/s),
? - kot, pod katerim je telo vrženo proti obzorju (°),
g- pospešek prostega pada 9,81 (m/s2),
tsmax- skupni čas potovanja (s)

Gibanje telesa, vrženega pod kotom na vodoravno ravnino

Oglejmo si gibanje telesa, vrženega s hitrostjo V 0, katerega vektor je usmerjen pod kotom α glede na obzorje, v ravnini XOY, tako da telo v trenutku metanja postavimo v izhodišče koordinat, kot je prikazano na sliki 1.

V odsotnosti upornih sil lahko gibanje telesa, vrženega pod kotom na obzorje, obravnavamo kot poseben primer krivuljnega gibanja pod vplivom gravitacije. Uporaba 2. Newtonovega zakona

Slika 1 je usmerjena navzgor, v primeru, ko je os OY usmerjena navzdol, potem projekcija vektorja

2 a na osi op-amp bo pozitiven(ob branju pogojev nalog si sami izberite smer osi, če to ni navedeno v pogojih).

Vrednosti projekcij vektorja pospeška a na osi OX in OU dajejo razlog za to

naslednji izhod:

∙ telo, vrženo pod kotom na vodoravno, hkrati sodeluje v dveh gibanjih - enakomerno vodoravno in enakomerno spremenljivo vzdolž

Za enakomerno spremenljivo gibanje so odvisnosti hitrosti in premika od časa podane z enačbami:

koordinate telesa v trenutku t.

Med njegovim gibanjem t (od trenutka meta do trenutka padca na isto

ravni) se telo dvigne na največjo višino hmax, se z nje spusti in odleti od mesta meta na razdalji L (domet letenja) - glej sliko 1.

1) Čas gibanja telesa t je mogoče najti ob upoštevanju vrednosti telesnih koordinat Sy v

Če nadomestimo vrednosti Voya in (14) v drugo enačbo sistema (13), dobimo

2) Domet letenja L je mogoče najti ob upoštevanju vrednosti koordinat telesa Sх in

začetni trenutek časa in čas t (glej sliko 1)

Če nadomestimo vrednosti Vox in (17) v prvo enačbo sistema (13), dobimo

3) Največja višina dviga h maks je mogoče najti glede na vrednost

hitrost telesa V na točki največjega dviga telesa

Primerjava vrednosti (16) in (22) daje razloge za sklep

· čas gibanja do višine največjega dviga telesa (t pod ) je enak času spusta telesa (tп) s te višine in je enak polovici časa celotnega gibanja telesa od trenutka metanja do trenutka padca na isto raven

Preučevanje gibanja telesa, vrženega s hitrostjo V 0, katerega vektor je usmerjen pod kotom α na vodoravno ravnino, je na računalniškem modelu zelo nazorno.

"Prosti pad teles" v zbirki računalniških modelov "Odprta fizika"

Podjetje PHYSICON. V tem modelu lahko nastavite različne začetne pogoje.

Primer, ki smo ga obravnavali, je treba na primer določiti (ukaz »Počisti«) z začetnim pogojem h = 0 in izbranima V0 in α. Ukaz "Start" bo prikazal gibanje telesa in dal sliko trajektorije gibanja in smeri vektorjev hitrosti telesa v določenih trenutkih časa.

Slika 2. Pogovorno okno računalniškega modela "Prosti pad teles" v razdelku

"Mehanika"; telo se premakne iz izhodišča in pade na isto raven.

Če se stanje problema razlikuje od primera, ki smo ga obravnavali, potem je potrebno

za rešitev problema z izbiro smeri osi postavite telo v začetni trenutek

čas, upodabljajo tirnico telesa do točke padca, torej

z določitvijo koordinat telesa v začetnem in končnem trenutku časa. Potem

uporabite enačbe (3), (5), (8) in (9) kot osnovo za rešitev in obravnavano zgoraj

algoritem za rešitev problema.

Razmislimo o posebnih primerih.

6 1. Telo je vrglo na hitrost V 0 , katerega vektor je usmerjen pod kotomα do

obzorju, z višine h in je padel na razdalji L od točke metanja. y na začetnico

in vrednosti preostalih koordinat bodo izbrane na enak način, kot smo izbrali.

Slika 3. Pogovorno okno računalniškega modela "Prosti pad teles" v razdelku

"Mehanika"; telo se premakne iz točke h = 50m in pade na ničelno raven.

2. Telo je vrglo vodoravno s hitrostjo V 0 z višine h in je padlo na razdalji L od mesta meta. Razlika od primera, ki smo ga obravnavali, je v tem, da vrednosti telesnih koordinat S l v začetnem trenutku bo prav tako določena z enačbo (25),

in vrednosti preostalih koordinat bodo izbrane na enak način, kot smo izbrali. Toda v tem primeru je začetna hitrost telesa v projekciji na os OU enaka nič (ker je α = 0), tj.

projekciji vektorja začetne hitrosti na osi OX in OU sta enaki

Slika 4. Pogovorno okno računalniškega modela "Prosti pad teles" v razdelku

"Mehanika"; vodoravno vrženo telo se premakne iz točke h = 50m in pade na ničelno raven.

Spodaj so pogoji težav in skenirane rešitve. Če morate rešiti problem na to temo, lahko tukaj najdete podoben pogoj in svojega rešite po analogiji. Nalaganje strani lahko traja nekaj časa zaradi velikega števila slik. Če potrebujete reševanje problemov ali spletno pomoč pri fiziki, nas kontaktirajte, z veseljem vam bomo pomagali.

Načelo reševanja teh problemov je razgradnja hitrosti prosto padajočega telesa na dve komponenti - vodoravno in navpično. Horizontalna komponenta hitrosti je konstantna, vertikalno gibanje poteka s pospeškom prostega pada g=9,8 m/s 2 . Uporabimo lahko tudi zakon o ohranitvi mehanske energije, po katerem je vsota potencialne in kinetične energije telesa v tem primeru konstantna.

Materialna točka je vržena pod kotom na obzorje z začetno hitrostjo 15 m/s. Začetna kinetična energija je 3-krat večja od kinetične energije točke na zgornji točki trajektorije. Kako visoko se je dvignila točka?

Telo je vrženo pod kotom 40 stopinj glede na horizontalo z začetno hitrostjo 10 m/s. Poiščite razdaljo, ki jo bo telo preletelo, preden bo padlo, višino vzpona na zgornji točki trajektorije in čas leta.

Telo vržemo s stolpa višine H pod kotom α proti vodoravnici z začetno hitrostjo v. Poiščite razdaljo od stolpa do mesta, kjer je truplo padlo.

Telo z maso 0,5 kg vržemo s površja Zemlje pod kotom 30 stopinj na vodoravno površino z začetno hitrostjo 10 m/s. Poiščite potencialno in kinetično energijo telesa po 0,4 s.

Materialna točka je vržena navzgor z zemeljske površine pod kotom na obzorje z začetno hitrostjo 10 m/s. Določite hitrost točke na višini 3 m.

Telo je vrženo navzgor od zemeljske površine pod kotom 60 stopinj z začetno hitrostjo 10 m/s. Poiščite razdaljo do točke trka, hitrost telesa na točki trka in čas leta.

Telo vržemo navzgor pod kotom na vodoravno z začetno hitrostjo 20 m/s. Razdalja do točke padca je 4-kratna največja višina dviga. Poiščite kot, pod katerim je telo vrženo.

Telo vržemo z višine 5 m pod kotom 30 stopinj proti vodoravnici z začetno hitrostjo 22 m/s. Poišči domet in čas leta telesa.

Telo vržemo z zemeljskega površja pod kotom na obzorje z začetno hitrostjo 30 m/s. Poiščite tangencialni in normalni pospešek telesa 1s po metu.

Telo je vrženo s površine Zesli pod kotom 30 stopinj proti vodoravnici z začetno hitrostjo 14,7 m/s. Poiščite tangencialni in normalni pospešek telesa 1,25 s po metu.

Telo je vrženo pod kotom 60 stopinj glede na horizontalo z začetno hitrostjo 20 m/s. Po kolikšnem času bo kot med hitrostjo in obzorjem postal 45 stopinj?

Vržena žoga v telovadnici pod kotom obzorja,z začetno hitrostjo 20 m/s se je na zgornji točki trajektorije dotaknil stropa na višini 8 m in padel na določeni razdalji od mesta meta. Poiščite to razdaljo in kot, pod katerim je telo vrženo.

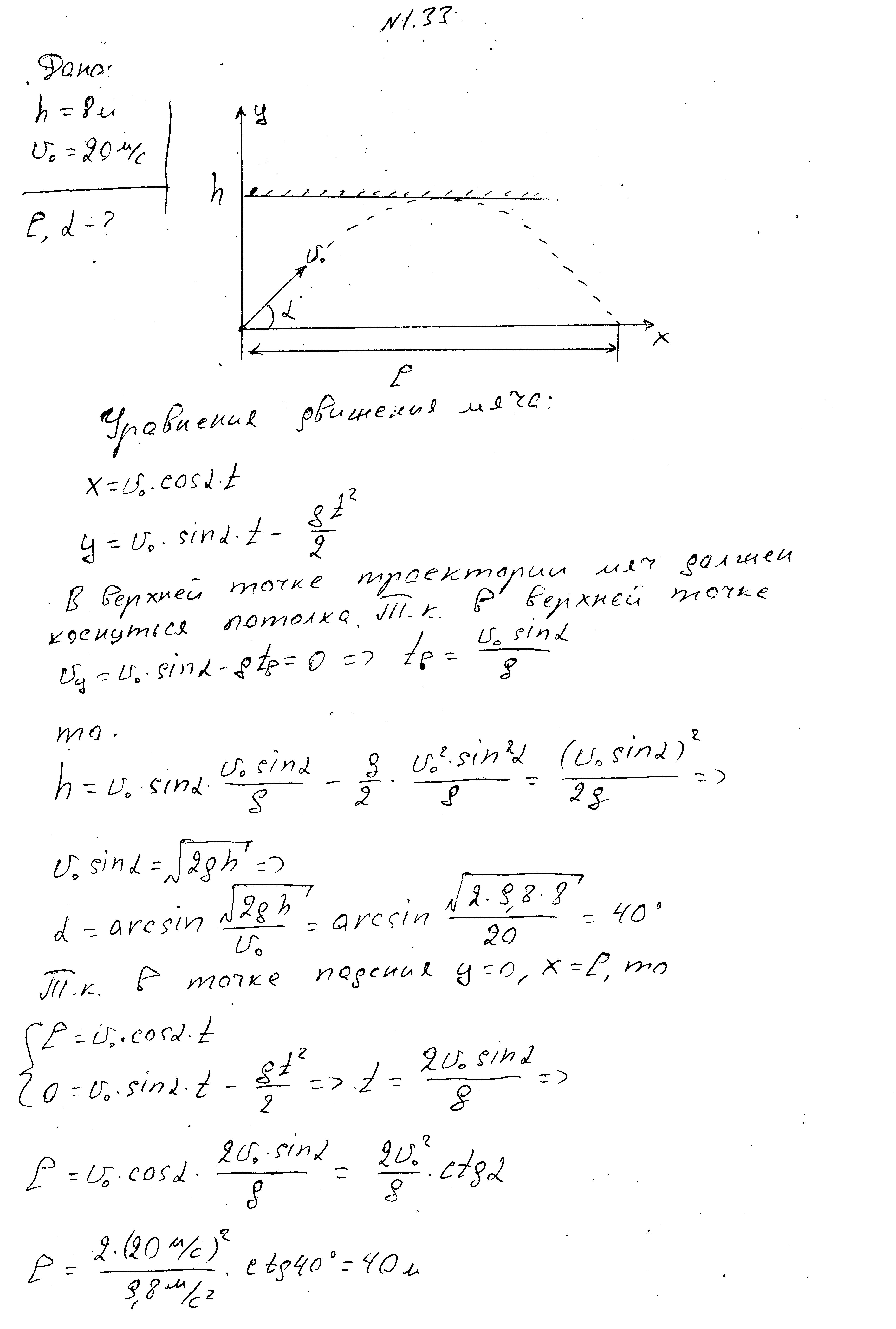
Telo, vrženo s površja Zemlje pod kotom na obzorje, je padlo po 2,2 s. Poiščite največjo višino dviga telesa.

Kamen je vržen pod kotom 30 stopinj glede na vodoravno ravnino. Kamen je dvakrat dosegel določeno višino - 1 s in 3 s po vrgu. Poiščite to višino in začetno hitrost kamna.

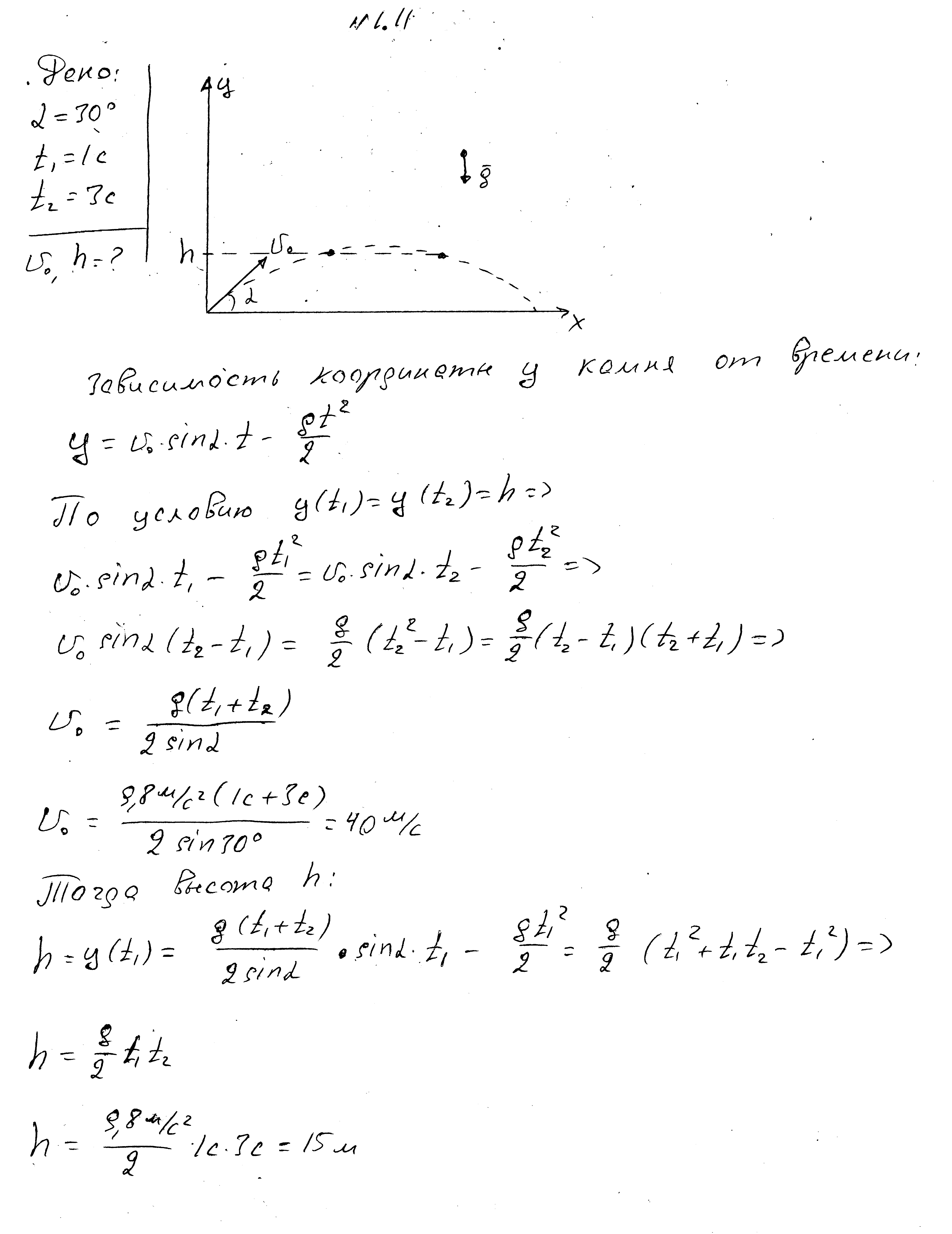
Kamen je vržen pod kotom 30 stopinj glede na vodoravno površino z začetno hitrostjo 10 m/s. Poiščite razdaljo od točke metanja do kamna po 4 s.

Projektil se izstreli v trenutku, ko letalo preleti top, pod kotom na obzorje z začetno hitrostjo 500 m/s. Granata je zadela letalo na višini 3,5 km 10 sekund po izstrelitvi. Kakšna je hitrost letala?

Topovsko kroglo z maso 5 kg vržemo s površine Zemlje pod kotom 60 stopinj na vodoravno ravnino. Energija, porabljena za pospeševanje teže, je 500 J. Določite domet in čas leta.

Telo vržemo z višine 100 m pod kotom 30 stopinj glede na vodoravno ravnino z začetno hitrostjo 5 m/s. Poiščite obseg letenja telesa.

Telo z maso 200 g, vrženo s površine Zemlje pod kotom na obzorje, je po času 1,2 s padlo na razdaljo 5 m. Poiščite službo za metanje telesa.