Številski krog v negativni smeri. Osnovne količine številskega kroga

Številčni krog je enotski krog, katerega točke ustrezajo določenim realnim številom.

Enotski krog je krog s polmerom 1.

Splošni pogled na številski krog.

1) Njegov polmer je vzet kot merska enota.

2) Vodoravni in navpični premer delita številski krog na štiri četrtine. Imenujejo se prva, druga, tretja in četrta četrtina.

3) Vodoravni premer je označen z AC, pri čemer je A skrajni desno pika.
Navpični premer je označen z BD, pri čemer je B najvišja točka.
Oziroma:

prva četrtina je lok AB

druga četrtina - lok pr

tretja četrtina - lok CD

četrta četrtina - lok DA

4) Začetna točka številskega kroga je točka A.

Štetje vzdolž številskega kroga lahko poteka v smeri urinega kazalca ali v nasprotni smeri urinega kazalca.

Računamo od točke A proti v smeri urinega kazalca se imenuje pozitivno smer.

Računamo od točke A Avtor: imenovano v smeri urinega kazalca negativno smer.

Številčni krog vklopljen koordinatna ravnina.

Središče polmera številskega kroga ustreza izhodišču (število 0).

Vodoravni premer ustreza osi x, navpična - os l.

Izhodišče Številski krogtee je na osixin ima koordinate (1; 0).

Imena in lokacije glavnih točk na številskem krogu:

Kako si zapomniti imena številskih krogov.

Obstaja več preprostih vzorcev, ki vam bodo pomagali enostavno zapomniti osnovna imena številskega kroga.

Preden začnemo, naj vas spomnimo: štetje poteka v pozitivni smeri, to je od točke A (2π) v nasprotni smeri urinega kazalca.

1) Začnimo z skrajne točke na koordinatnih oseh.

Začetna točka je 2π (skrajna desna točka na osi X, enako 1).

Kot veste, je 2π obseg kroga. To pomeni, da je polovica kroga 1π ali π. os X deli krog točno na pol. V skladu s tem je skrajna leva točka na osi X enako -1 se imenuje π.

Najvišja točka na osi pri, enako 1, deli zgornji polkrog na pol. To pomeni, da če je polkrog π, potem je polkrog π/2.

Hkrati je π/2 tudi četrtina kroga. Preštejmo tri takšne četrtine od prve do tretje - in prišli bomo do najnižje točke na osi pri, enako -1. Če pa vključuje tri četrtine, potem je njegovo ime 3π/2.

2) Zdaj pa preidimo na preostale točke. Prosimo, upoštevajte: vse nasprotne točke imajo isti imenovalec- in to so nasprotne točke in glede na os pri, tako glede na sredino osi kot glede na os X. To nam bo pomagalo vedeti njihove vrednosti točk brez nabijanja.

Zapomniti si morate le pomen točk prve četrtine: π/6, π/4 in π/3. In potem bomo "videli" nekaj vzorcev:

- Glede na os pri v točkah druge četrtine, nasproti točkam prve četrtine, so števila v števcih za 1 manjša od velikosti imenovalcev. Za primer vzemimo točko π/6. Točka nasproti nje glede na os pri ima tudi 6 v imenovalcu in 5 v števcu (1 manj). To pomeni, da je ime te točke: 5π/6. Točka nasproti π/4 ima tudi 4 v imenovalcu in 3 v števcu (1 manj kot 4) - torej je točka 3π/4.
Točka nasproti π/3 ima prav tako 3 v imenovalcu in 1 manj v števcu: 2π/3.

- Glede na središče koordinatnih osi vse je obratno: števila v števcih nasprotnih točk (v tretji četrtini) za 1 večja vrednost imenovalci. Ponovno vzemimo točko π/6. Točka nasproti nje glede na središče ima prav tako 6 v imenovalcu, v števcu pa je številka za 1 večja - torej je 7π/6.
Točka nasproti točke π/4 ima prav tako 4 v imenovalcu, v števcu pa je številka za 1 večja: 5π/4.
Točka nasproti točke π/3 ima prav tako 3 v imenovalcu, v števcu pa je številka za 1 večja: 4π/3.

- Glede na os X(četrta četrtina) zadeva je bolj zapletena. Tukaj morate vrednosti imenovalca dodati številko, ki je za 1 manjša - ta vsota bo enaka številskemu delu števca nasprotne točke. Začnimo znova s ​​π/6. Vrednosti imenovalca, ki je enaka 6, dodamo število, ki je za 1 manjše od tega števila - to je 5. Dobimo: 6 + 5 = 11. To pomeni, da je nasproti osi X točka bo imela 6 v imenovalcu in 11 v števcu - to je 11π/6.

Točka π/4. Vrednosti imenovalca prištejemo za 1 manjše število: 4 + 3 = 7. To pomeni, da je nasproti osi. X točka ima 4 v imenovalcu in 7 v števcu - to je 7π/4.
Točka π/3. Imenovalec je 3. 3 prištejemo za ena manjše število - to je 2. Dobimo 5. To pomeni, da ima nasprotna točka v števcu 5 - in to je točka 5π/3.

3) Še en vzorec za točke središč četrtin. Jasno je, da je njihov imenovalec 4. Bodimo pozorni na števce. Števec sredine prve četrtine je 1π (vendar ni običajno pisati 1). Števec sredine druge četrtine je 3π. Števec sredine tretje četrtine je 5π. Števec sredine četrte četrtine je 7π. Izkazalo se je, da števci srednjih četrtin vsebujejo prve štiri lihe številke v naraščajočem vrstnem redu:
(1)π, 3π, 5π, 7π.
Tudi to je zelo preprosto. Ker imajo središča vseh četrtin v imenovalcu 4, jih že poznamo polna imena: π/4, 3π/4, 5π/4, 7π/4.

Značilnosti številskega kroga. Primerjava s številsko premico.

Kot veste, na številski premici vsaka točka ustreza ednina. Na primer, če je točka A na premici enaka 3, potem ne more biti več enaka nobenemu drugemu številu.

Na številskem krogu je drugače, ker je krog. Na primer, če želite priti iz točke A kroga v točko M, lahko to storite kot po ravni črti (samo mimo loka) ali pa obkrožite cel krog in nato pridete do točke M. Zaključek:

Naj bo točka M enaka nekemu številu t. Kot vemo, je obseg kroga 2π. To pomeni, da lahko točko t na krožnici zapišemo na dva načina: t ali t + 2π. To so enakovredne vrednosti.
To je t = t + 2π. Edina razlika je v tem, da ste v prvem primeru takoj prišli do točke M, ne da bi naredili krog, v drugem primeru pa ste naredili krog, a končali na isti točki M. Takih lahko naredite dve, tri ali dvesto krogi. Če število krogov označimo s črko n, potem dobimo nov izraz:
t = t + 2π n.

Od tod formula:

Definicija 1. Številčna os ( številska premica, koordinatna premica) Ox je premica, na kateri je izbrana točka O izvor (izhodišče koordinat)(slika 1), smer

O → x

naveden kot pozitivno smer in označen je segment, katerega dolžina se šteje za dolžinska enota.

Definicija 2. Odsek, katerega dolžina je vzeta kot enota dolžine, se imenuje merilo.

Vsaka točka na številski osi ima koordinato, ki je realno število. Koordinata točke O je nič. Koordinata poljubne točke A, ki leži na žarku Ox, je enaka dolžini odseka OA.

Koordinata poljubne točke A numerične osi, ki ne leži na žarku Ox, je negativna in v absolutni vrednosti enaka dolžini odseka OA. Definicija 3. Pravokotni kartezični koordinatni sistem Oxy na ravnini pokličite dva skupaj pravokotno numerični osi Ox in Oy z enako lestvico skupni začetek odštevanje v točki O in tako, da se rotacija od žarka Ox pod kotom 90° do žarka Oy izvaja v smeri v nasprotni smeri urinega kazalca(slika 2).

Opomba. Pravokotni kartezični koordinatni sistem Oxy, prikazan na sliki 2, se imenuje desni koordinatni sistem, za razliko od levi koordinatni sistem, pri katerem se vrtenje žarka Ox pod kotom 90° glede na žarek Oy izvaja v smeri urinega kazalca. V tem vodniku smo upoštevamo samo desnosučne koordinatne sisteme, ne da bi to posebej navedli.

Če na ravnini uvedemo nek sistem pravokotnih kartezičnih koordinat Oxy, bo vsaka točka ravnine pridobila dve koordinati – abscisa enako lestvico ordinata, ki se izračunajo na naslednji način. Naj bo A poljubna točka na ravnini. Iz točke A spustimo navpičnico A.A. 1 in A.A. 2 na ravne črte Ox oziroma Oy (slika 3).

Definicija 4. Abscisa točke A je koordinata točke A 1 na številski osi Ox je ordinata točke A koordinata točke A 2 na številski osi Oy.

Imenovanje Koordinate (abscisa in ordinata) točke A v pravokotnem kartezičnem koordinatnem sistemu običajno označimo z Oxy (slika 4). A(x;l) oz A = (x; l).

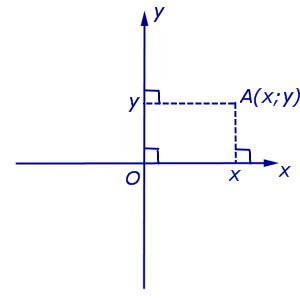
Opomba. Točka O, imenovana izvor, ima koordinate O(0 ; 0) .

Definicija 5. V pravokotnem kartezičnem koordinatnem sistemu Oxy numerično os Ox imenujemo abscisna os, numerično os Oy pa ordinatno os (slika 5).

Opredelitev 6. Vsak je pravokoten kartezični sistem koordinat deli ravnino na 4 četrtine (kvadrante), katerih oštevilčenje je prikazano na sliki 5.

Opredelitev 7. Imenuje se ravnina, na kateri je podan pravokotni kartezični koordinatni sistem koordinatna ravnina.

Opomba. Abscisna os je na koordinatni ravnini določena z enačbo l= 0 je ordinatna os podana na koordinatni ravnini z enačbo x = 0.

Izjava 1. Razdalja med dvema točkama koordinatna ravnina

A 1 (x 1 ;l 1) enako lestvico A 2 (x 2 ;l 2)

izračunano po formuli

Dokaz . Razmislite o sliki 6.

torej

Q.E.D.

Enačba krožnice na koordinatni ravnini

Oglejmo si na koordinatni ravnini Oxy (slika 7) krog s polmerom R s središčem v točki A 0 (x 0 ;l 0) .

Lekcija in predstavitev na temo: "Številski krog na koordinatni ravnini"

Dodatni materiali
Dragi uporabniki, ne pozabite pustiti svojih komentarjev, mnenj, želja! Vsa gradiva so bila preverjena s protivirusnim programom.

Priročniki in simulatorji v spletni trgovini Integral za 10. razred iz 1C
Algebraične naloge s parametri, 9.–11
Reševanje nalog iz geometrije. Interaktivne konstrukcijske naloge za 7.-10

Kaj bomo študirali:
1. Opredelitev.
2. Pomembne koordinate številskega kroga.
3. Kako najti koordinato številskega kroga?
4. Tabela glavnih koordinat številskega kroga.
5. Primeri reševanja problemov.

Definicija številskega kroga na koordinatni ravnini

Vsaka točka na številskem krogu ima svoje koordinate x in y v koordinatni ravnini in:
1) za $x > 0$, $y > 0$ - v prvem četrtletju;
2) za $x 0$ - v drugem četrtletju;
3) za $x 4) za $x > 0$, $y
Za poljubno točko $M(x; y)$ na številskem krogu so izpolnjene naslednje neenakosti: $-1
Zapomnite si enačbo številskega kroga: $x^2 + y^2 = 1$.

Pomembno je, da se naučimo poiskati koordinate točk na številskem krogu, prikazanem na sliki.

Poiščimo koordinato točke $\frac(π)(4)$

Koordinate točk na številskem krogu

Poglejmo si primere

rešitev:
45 $\frac(π)(4) = (10 + \frac(5)(4)) * π = 10π +5\frac(π)(4) = 5\frac(π)(4) + 2π*5 $.
To pomeni, da število $45\frac(π)(4)$ ustreza isti točki na številskem krogu kot število $\frac(5π)(4)$. Če pogledamo vrednost točke $\frac(5π)(4)$ v tabeli, dobimo: $P(\frac(45π)(4))=P(-\frac(\sqrt(2))( 2);-\frac (\sqrt(2))(2))$.

Primer 2.
Poiščite koordinato točke na številskem krogu: $P(-\frac(37π)(3))$.

rešitev:

Ker števili $t$ in $t+2π*k$, kjer je k celo število, ustrezata isti točki na številskem krogu, potem:
$-\frac(37π)(3) = -(12 + \frac(1)(3))*π = -12π –\frac(π)(3) = -\frac(π)(3) + 2π *(-6)$.
To pomeni, da število $-\frac(37π)(3)$ ustreza isti točki na številskem krogu kot število $–\frac(π)(3)$, število –$\frac(π) (3)$ ustreza isti točki kot $\frac(5π)(3)$. Če pogledamo vrednost točke $\frac(5π)(3)$ v tabeli, dobimo:
$P(-\frac(37π)(3))=P(\frac((1))(2);-\frac(\sqrt(3))(2))$.

Primer 3.
Poišči točke na številskem krogu z ordinato $y =\frac(1)(2)$ in zapiši, katerim številom $t$ ustrezajo?

rešitev:
Premica $y =\frac(1)(2)$ seka številski krog v točkah M in P. Točka M ustreza številu $\frac(π)(6)$ (iz podatkov tabele). To pomeni poljubno število v obliki: $\frac(π)(6)+2π*k$. Točka P ustreza številu $\frac(5π)(6)$ in torej poljubnemu številu v obliki $\frac(5π)(6) +2 π*k$.
Prejeli smo, kot se pogosto reče v takih primerih, dve seriji vrednosti:
$\frac(π)(6) +2 π*k$ in $\frac(5π)(6) +2π*k$.
Odgovor: $t=\frac(π)(6) +2 π*k$ in $t=\frac(5π)(6) +2π*k$.

Primer 4.
Poiščite točke na številskem krogu z absciso $x≥-\frac(\sqrt(2))(2)$ in zapišite, katerim številom $t$ ustrezajo.

rešitev:

Premica $x =-\frac(\sqrt(2))(2)$ seka številski krog v točkah M in P. Neenakost $x≥-\frac(\sqrt(2))(2)$ ustreza do točk loka PM. Točka M ustreza številu $3\frac(π)(4)$ (iz podatkov tabele). To pomeni poljubno število v obliki $-\frac(3π)(4) +2π*k$. Točka P ustreza številu $-\frac(3π)(4)$ in torej poljubnemu številu v obliki $-\frac(3π)(4) +2π*k$.

Potem dobimo $-\frac(3π)(4) +2 π*k ≤t≤\frac(3π)(4) +2πk$.

Odgovor: $-\frac(3π)(4) +2 π*k ≤t≤\frac(3π)(4) +2πk$.

Težave, ki jih je treba rešiti neodvisno

Če na koordinatno ravnino postavite številski krog enote, lahko najdete koordinate za njegove točke. Številski krog je postavljen tako, da njegovo središče sovpada z izhodiščem ravnine, to je s točko O (0; 0).

Običajno so na krogu številk enote označene točke, ki ustrezajo izhodišču kroga

• četrtine - 0 ali 2π, π/2, π, (2π)/3,
• srednje četrtine - π/4, (3π)/4, (5π)/4, (7π)/4,
• tretjine četrtin - π/6, π/3, (2π)/3, (5π)/6, (7π)/6, (4π)/3, (5π)/3, (11π)/6.

Na koordinatni ravnini z zgornjo lokacijo enotskega kroga lahko najdete koordinate, ki ustrezajo tem točkam kroga.

Koordinate koncev četrtin je zelo enostavno najti. V točki 0 kroga je koordinata x 1, koordinata y pa 0. Označimo jo lahko kot A (0) = A (1; 0).

Konec prvega četrtletja bo na pozitivni osi y. Zato je B (π/2) = B (0; 1).

Konec druge četrtine je na negativni pol-osi: C (π) = C (-1; 0).

Konec tretje četrtine: D ((2π)/3) = D (0; -1).

Toda kako najti koordinate središč četrtin? Če želite to narediti, sestavite pravokotni trikotnik. Njegova hipotenuza je odsek od središča kroga (ali izhodišča) do sredine četrtine kroga. To je polmer kroga. Ker obstaja enotski krog, je hipotenuza enaka 1. Nato narišite pravokotno iz točke na krogu na poljubno os. Naj bo proti osi x. Rezultat je pravokotni trikotnik, katerega dolžine krakov sta koordinati x in y točke na krogu.

Četrtina kroga je 90º. In pol četrtine je 45º. Ker je hipotenuza narisana na središče kvadranta, je kot med hipotenuzo in krakom, ki se razteza iz izhodišča, 45°. Toda vsota kotov katerega koli trikotnika je 180º. Posledično ostane tudi kot med hipotenuzo in drugo nogo 45º. Posledica tega je enakokraki pravokotni trikotnik.

Iz Pitagorovega izreka dobimo enačbo x 2 + y 2 = 1 2. Ker je x = y in 1 2 = 1, se enačba poenostavi na x 2 + x 2 = 1. Če jo rešimo, dobimo x = √½ = 1/√2 = √2/2.

Tako so koordinate točke M 1 (π/4) = M 1 (√2/2; √2/2).

V koordinatah središč drugih četrtin se bodo spremenili samo znaki, moduli vrednosti pa bodo ostali enaki, saj bo desni trikotnik le obrnjen. Dobimo:
M 2 ((3π)/4) = M 2 (-√2/2; √2/2)
M 3 ((5π)/4) = M 3 (-√2/2; -√2/2)
M 4 ((7π)/4) = M 4 (√2/2; -√2/2)

Pri določanju koordinat tretjih delov četrtin kroga se sestavi tudi pravokotni trikotnik. Če vzamemo točko π/6 in narišemo pravokotno na os x, bo kot med hipotenuzo in krakom, ki leži na osi x, 30º. Znano je, da noga, ki leži nasproti kota 30º enaka polovici hipotenuza. To pomeni, da smo našli koordinato y, enaka je ½.

Če poznamo dolžine hipotenuze in enega od krakov, z uporabo Pitagorovega izreka najdemo drugi krak:
x 2 + (½) 2 = 1 2
x 2 = 1 - ¼ = ¾
x = √3/2

Tako je T 1 (π/6) = T 1 (√3/2; ½).

Za točko druge tretjine prve četrtine (π/3) je bolje narisati pravokotno os na os y. Potem bo tudi kot v izhodišču 30º. Tu bo koordinata x enaka ½, y pa √3/2: T 2 (π/3) = T 2 (½; √3/2).

Za druge točke tretjih četrtin se bodo znaki in vrstni red vrednosti koordinat spremenili. Vse točke, ki so bližje osi x, bodo imele koordinatno vrednost modula x enako √3/2. Tiste točke, ki so bližje osi y, bodo imele vrednost modula y enako √3/2.
T 3 ((2π)/3) = T 3 (-½; √3/2)
T 4 ((5π)/6) = T 4 (-√3/2; ½)
T 5 ((7π)/6) = T 5 (-√3/2; -½)
T 6 ((4π)/3) = T 6 (-½; -√3/2)
T 7 ((5π)/3) = T 7 (½; -√3/2)
T 8 ((11π)/6) = T 8 (√3/2; -½)

Če želite uporabljati predogled predstavitev, ustvarite račun zase ( račun) Google in se prijavite: https://accounts.google.com

Podnapisi diapozitivov:

Številski krog v koordinatni ravnini

Ponovimo: Enotni krog– številski krog s polmerom 1. R=1 C=2 π + - y x

Če točka M številskega kroga ustreza številu t, potem ustreza tudi številu oblike t+2 π k, kjer je k poljubno celo število (k ϵ Z). M(t) = M(t+2 π k), kjer je k ϵ Z

Osnovne postavitve Prva postavitev 0 π y x Druga postavitev y x

x y 1 A(1, 0) B (0, 1) C (- 1, 0) D (0, -1) 0 x>0 y>0 x 0 x 0 y

Poiščimo koordinate točke M, ki ustreza točki. 1) 2) x y M P 45° O A

Koordinate glavnih točk prve postavitve 0 2 x 1 0 -1 0 1 y 0 1 0 -1 0 0 x 1 0 -1 0 1 y 0 1 0 -1 0 D y x

M P x y O A Poiščimo koordinate točke M, ki ustreza točki. 1) 2) 30°

M P Poiščite koordinate točke M, ki ustreza točki. 1) 2) 30° x y O A B

Z uporabo lastnosti simetrije najdemo koordinate točk, ki so večkratniki y x

Koordinate glavnih točk druge postavitve x y x y y x

Primer Poiščite koordinate točke na številskem krogu. Rešitev: P y x

Primer Poiščite točke z ordinato na številskem krogu Rešitev: y x ​​​​x y x y

Vaje: Poiščite koordinate točk na številskem krogu: a) , b) . Na številskem krogu poiščite točke z absciso.

Koordinate glavnih točk 0 2 x 1 0 -1 0 1 y 0 1 0 -1 0 0 x 1 0 -1 0 1 y 0 1 0 -1 0 Koordinate glavnih točk prve postavitve x y x y Koordinate glavnih točke druge postavitve

Na temo: metodološki razvoj, predstavitve in zapiski

Didaktično gradivo o algebri in začetki analize v 10. razredu (stopnja profila) "Številski krog na koordinatni ravnini"

Možnost 1.1 Poišči točko na številskem krogu: A) -2∏/3B) 72. Katera četrtina številskega kroga je točka 16.3.