Binomska porazdelitev naključnih spremenljivk in njene lastnosti. Binomska porazdelitev naključne spremenljivke

Verjetnostne porazdelitve diskretnih naključnih spremenljivk. Binomska porazdelitev. Poissonova porazdelitev. Geometrijska porazdelitev. Generirajoča funkcija.

6. Verjetnostne porazdelitve diskretnih naključnih spremenljivk

6.1. Binomska porazdelitev

Naj se proizvaja n neodvisni preizkušnji, v vsaki od njih dogodek A Lahko se pojavi ali pa ne. Verjetnost str pojav dogodka A pri vseh testih stalna in se od testa do testa ne spreminja. Kot naključno spremenljivko X upoštevajte število pojavitev dogodka A v teh testih. Formula za iskanje verjetnosti, da se zgodi dogodek A gladka k enkrat na vsak n testi, kot je znano, so opisani Bernoullijeva formula

Porazdelitev verjetnosti, definirana z Bernoullijevo formulo, se imenuje binom .

Ta zakon se imenuje "binom", ker lahko desno stran obravnavamo kot splošni izraz v razširitvi Newtonovega binoma.

Zapišimo binomski zakon v obliki tabele

Poiščimo numerične značilnosti te porazdelitve.

Po definiciji matematično pričakovanje za DSV imamo

.

Zapišimo enačbo, ki je dvojiška od Newtona

.

in ga ločite glede na p. Kot rezultat dobimo

.

Pomnožimo levo in desna stran na str:

.

Glede na to str+ q=1, imamo

(6.2)

Torej, matematično pričakovanje števila pojavitev dogodkov vnneodvisnih poskusov je enako zmnožku števila poskusovnna verjetnoststrpojav dogodka v vsakem poskusu.

Izračunajmo varianco s formulo

.

Za to bomo našli

.

Najprej dvakrat razločimo Newtonovo binomsko formulo glede na str:

in obe strani enakosti pomnožimo s str 2:

torej

Torej je varianca binomske porazdelitve

. (6.3)

Te rezultate je mogoče dobiti tudi s povsem kvalitativnim razmišljanjem. Skupno število X pojavitev dogodka A v vseh poskusih je vsota števila pojavitev dogodka v posameznih poskusih. Torej, če je X 1 število pojavitev dogodka v prvem poskusu, X 2 – v drugem itd., potem skupno število pojavov dogodka A v vseh poskusih je enako X=X 1 +X 2 +…+X n. Glede na lastnost matematičnega pričakovanja:

Vsak od členov na desni strani enakosti je matematično pričakovanje števila dogodkov v enem poskusu, ki je enako verjetnosti dogodka. torej

Glede na lastnost disperzije:

Ker je , in matematično pričakovanje naključne spremenljivke , ki ima lahko samo dve vrednosti, in sicer 1 2 z verjetnostjo str in 0 2 z verjetnostjo q, To
. torej
Kot rezultat dobimo

Z uporabo koncepta začetnega in osrednjega momenta lahko dobimo formule za asimetrijo in kurtozo:

. (6.4)

riž. 6.1

številkam 0 pojav dogodka imenujemonajverjetneje , če je verjetnost, da se dogodek zgodi določeno število krat v tej seriji testov, največja (največja v porazdelitvenem poligonu). Za binomsko porazdelitev

Komentiraj. To neenakost je mogoče dokazati z uporabo rekurentne formule za binomske verjetnosti:

(6.6)

Primer 6.1. Delež premium izdelkov v tem podjetju je 31%. Kakšna sta matematično pričakovanje in varianca ter najverjetnejše število vrhunskih izdelkov v naključno izbrani seriji 75 izdelkov?

rešitev. Ker str=0,31, q=0,69, n= 75, torej

M[ X] = n.p.= 750,31 = 23,25; D[ X] = npq = 750,310,69 = 16,04.

Da bi našli najverjetnejšo številko m 0, ustvarimo dvojno neenakost

Iz tega sledi m 0 = 23.

Razmislimo Binomska porazdelitev, izračunajmo njegovo matematično pričakovanje, disperzijo in način. S pomočjo funkcije MS EXCEL BINOM.DIST() bomo zgradili grafe porazdelitvene funkcije in gostote verjetnosti. Ocenimo porazdelitveni parameter p, matematično pričakovanje porazdelitve in standardni odklon. Upoštevajmo tudi Bernoullijevo porazdelitev.

Opredelitev. Naj se odvijajo n testov, pri katerih se lahko zgodita samo 2 dogodka: dogodek »uspeh« z verjetnostjo str ali dogodek »napake« z verjetnostjo q =1-p (tako imenovani Bernoullijeva shema,Bernoulliposkusi).

Verjetnost prejema točno x uspeh pri teh n testi je enako:

Število uspehov v vzorcu x je naključna spremenljivka, ki ima Binomska porazdelitev(angleščina) Binomdistribucija) str in n– so parametri te porazdelitve.

Zapomnite si, da morate uporabiti Bernoullijeve sheme in temu primerno Binomska porazdelitev, izpolnjeni morajo biti naslednji pogoji:

• Vsak test mora imeti natanko dva izida, ki se običajno imenujeta "uspeh" in "neuspeh".
• rezultat posameznega testa ne sme biti odvisen od rezultatov prejšnjih testov (test neodvisnosti).
• verjetnost uspeha str mora biti konstantna za vse teste.

Binomska porazdelitev v MS EXCEL

V MS EXCEL, od različice 2010, za Binomska porazdelitev obstaja funkcija BINOM.DIST(), angleško ime- BINOM.DIST(), ki omogoča izračun verjetnosti, da bo vzorec natančno vseboval X"uspeh" (tj. funkcija gostote verjetnosti p(x), glej formulo zgoraj) in kumulativna porazdelitvena funkcija(verjetnost, da bo imel vzorec x ali manj "uspehov", vključno z 0).

Pred MS EXCEL 2010 je imel EXCEL funkcijo BINOMDIST(), ki omogoča tudi izračun distribucijska funkcija in gostota verjetnosti p(x). BINOMIST() je opuščen v MS EXCEL 2010 zaradi združljivosti.

Primer datoteke vsebuje grafe porazdelitev gostote verjetnosti in .

Binomska porazdelitev ima oznako B(n; str) .

Opomba: Za gradnjo integralna funkcija distribucija popolni tipski diagram Urnik, Za gostota porazdelitve – Histogram z združevanjem. Za več informacij o ustvarjanju grafikonov preberite članek Osnovne vrste grafikonov.

Opomba: Za lažje pisanje formul so bila v vzorčni datoteki ustvarjena imena za parametre Binomska porazdelitev: n in str.

Primer datoteke prikazuje različne izračune verjetnosti z uporabo funkcij MS EXCEL:

Kot lahko vidite na zgornji sliki, se predpostavlja, da:

• Neskončna populacija, iz katere je vzet vzorec, vsebuje 10 % (ali 0,1) veljavnih elementov (parameter str, tretji argument funkcije = BINOM.DIST() )
• Za izračun verjetnosti, da bo v vzorcu 10 elementov (parameter n, drugi argument funkcije) bo natanko 5 veljavnih elementov (prvi argument), napisati morate formulo: =BINOM.DIST(5, 10, 0,1, FALSE)
• Zadnji, četrti element je nastavljen = FALSE, tj. vrednost funkcije je vrnjena gostota porazdelitve.

Če je vrednost četrtega argumenta = TRUE, potem funkcija BINOM.DIST() vrne vrednost kumulativna porazdelitvena funkcija ali samo Distribucijska funkcija. V tem primeru lahko izračunate verjetnost, da bo število dobrih elementov v vzorcu iz določenega obsega, na primer 2 ali manj (vključno z 0).

Če želite to narediti, morate napisati formulo:
= BINOM.DIST(2; 10; 0,1; TRUE)

Opomba: Za vrednost x, ki ni celo število, . Naslednje formule bodo na primer vrnile isto vrednost:
=BINOM.DIST( 2 ; 10; 0,1; TRUE)
=BINOM.DIST( 2,9 ; 10; 0,1; TRUE)

Opomba: V vzorčni datoteki gostota verjetnosti in distribucijska funkcija izračunano tudi z uporabo definicije in funkcije NUMBERCOMB().

Indikatorji distribucije

IN primer datoteke na delovnem listu Primer Obstajajo formule za izračun nekaterih kazalnikov distribucije:

• =n*p;
• (standardni odklon na kvadrat) = n*p*(1-p);
• = (n+1)*p;
• =(1-2*p)*ROOT(n*p*(1-p)).

Izpeljimo formulo matematično pričakovanje Binomska porazdelitev uporabo Bernoullijevo vezje.

Po definiciji naključna spremenljivka X in Bernoullijeva shema(Bernoullijeva naključna spremenljivka) ima distribucijska funkcija:

Ta distribucija se imenuje Bernoullijeva porazdelitev.

Opomba: Bernoullijeva porazdelitev – poseben primer Binomska porazdelitev s parametrom n=1.

Ustvarimo 3 nize po 100 števil z različnimi verjetnostmi uspeha: 0,1; 0,5 in 0,9. Če želite to narediti v oknu Generacija naključna števila Za vsako verjetnost p nastavimo naslednje parametre:

Opomba: Če nastavite možnost Naključno razprševanje (Naključno seme), potem lahko izberete določen naključni niz ustvarjenih števil. Na primer, če nastavite to možnost =25, lahko ustvarite iste nize naključnih števil na različnih računalnikih (če so seveda drugi parametri porazdelitve enaki). Vrednost možnosti ima lahko celoštevilske vrednosti od 1 do 32.767 Ime možnosti Naključno razprševanje lahko zmede. Bolje bi bilo prevesti kot Pokličite številko z naključnimi številkami.

Kot rezultat bomo imeli 3 stolpce s 100 številkami, na podlagi katerih lahko ocenimo npr. verjetnost uspeha str po formuli: Število uspehov/100(cm. primer datoteke GenerationBernoulli).

Opomba: Za Bernoullijeve porazdelitve s p=0,5 lahko uporabite formulo =RANDBETWEEN(0;1), ki ustreza .

Generiranje naključnih števil. Binomska porazdelitev

Predpostavimo, da je v vzorcu 7 izdelkov z napako. To pomeni, da je »zelo verjetno«, da se je delež izdelkov z napako spremenil str, kar je značilnost našega proizvodni proces. Čeprav je taka situacija »zelo verjetna«, obstaja možnost (tveganje alfa, napaka tipa 1, »lažni alarm«), da str ostala nespremenjena, povečano število izdelkov z napako pa je posledica naključnega vzorčenja.

Kot je razvidno iz spodnje slike, je 7 število izdelkov z napako, ki je sprejemljivo za postopek s p=0,21 pri enaki vrednosti Alfa. To ponazarja, da ko je mejna vrednost pomanjkljivih predmetov v vzorcu presežena, str»najverjetneje« se je povečalo. Besedna zveza "najverjetneje" pomeni, da obstaja le 10-odstotna verjetnost (100%-90%), da je odstopanje odstotka okvarjenih izdelkov nad mejno vrednostjo samo zaradi naključnih razlogov.

Tako lahko prekoračitev mejnega števila izdelkov z napako v vzorcu služi kot signal, da je proces moten in je začel proizvajati rabljene izdelke. O višji odstotek izdelkov z napako.

Opomba: Pred MS EXCEL 2010 je imel EXCEL funkcijo CRITBINOM(), ki je enakovredna BINOM.INV(). CRITBINOM() je opuščen v MS EXCEL 2010 in novejšem zaradi združljivosti.

Povezava binomske porazdelitve z drugimi porazdelitvami

Če je parameter n Binomska porazdelitev teži v neskončnost in str teži k 0, potem v tem primeru Binomska porazdelitev se lahko približa.
Lahko oblikujemo pogoje, ko je aproksimacija Poissonova porazdelitev deluje dobro:

• str<0,1 (manj str in več n, bolj natančen je približek);
• str>0,9 (glede na to q=1- str, izračune v tem primeru je treba opraviti skozi q(A X je treba zamenjati z n- x). Zato manj q in več n, bolj natančen je približek).

Pri 0,1<=p<=0,9 и n*p>10 Binomska porazdelitev se lahko približa.

v zameno, Binomska porazdelitev lahko služi kot dober približek, ko je velikost populacije N Hipergeometrična porazdelitev veliko večji od velikosti vzorca n (tj. N>>n ali n/N<<1).

Več podrobnosti o razmerju med zgornjimi porazdelitvami najdete v članku. Navedeni so tudi primeri aproksimacije in pojasnjeni so pogoji, kdaj je to mogoče in s kakšno natančnostjo.

NASVET: O drugih distribucijah MS EXCEL si lahko preberete v članku.

Binomska porazdelitev je ena najpomembnejših verjetnostnih porazdelitev diskretno spremenljive naključne spremenljivke. Binomska porazdelitev je verjetnostna porazdelitev števila m pojav dogodka A V n medsebojno neodvisna opazovanja. Pogosto dogodek A se imenuje "uspeh" opazovanja, nasprotni dogodek pa se imenuje "neuspeh", vendar je ta oznaka zelo pogojna.

Pogoji binomske porazdelitve:

• skupaj izvedenih n sojenja, v katerih dogodek A se lahko pojavi ali ne;
• dogodek A v vsakem testu se lahko pojavi z enako verjetnostjo str;
• testi so med seboj neodvisni.

Verjetnost, da v n dogodek testiranja A točno bo prišlo m krat, se lahko izračuna z uporabo Bernoullijeve formule:

,

kje str- verjetnost nastanka dogodka A;

q = 1 - str- verjetnost pojava nasprotnega dogodka.

Ugotovimo zakaj je binomska porazdelitev povezana z Bernoullijevo formulo na zgoraj opisan način? . Dogodek - število uspehov pri n testi so razdeljeni na več možnosti, pri vsaki od katerih je dosežen uspeh m testi in neuspeh - v n - m testi. Razmislimo o eni od teh možnosti - B1 . S pravilom za seštevanje verjetnosti pomnožimo verjetnosti nasprotnih dogodkov:

,

in če označimo q = 1 - str, To

.

Katero koli drugo možnost, pri kateri m uspeh in n - m neuspehi. Število takih možnosti je enako številu načinov, na katere lahko n test dobiti m uspeh.

Vsota vseh verjetnosti mštevilo dogodkov A(številke od 0 do n) je enako ena:

kjer vsak člen predstavlja člen v Newtonovem binomu. Zato se obravnavana porazdelitev imenuje binomska porazdelitev.

V praksi je pogosto treba izračunati verjetnosti "ne več kot m uspeh v n testi" ali "vsaj m uspeh v n testi". Za to se uporabljajo naslednje formule.

Integralna funkcija, tj verjetnost F(m) kaj je notri n opazovalni dogodek A nič več ne bo prišlo m enkrat, se lahko izračuna po formuli:

Po vrsti verjetnost F(≥m) kaj je notri n opazovalni dogodek A ne bo prišlo nič manj m enkrat, se izračuna po formuli:

Včasih je bolj priročno izračunati verjetnost, da n opazovalni dogodek A nič več ne bo prišlo m krat, skozi verjetnost nasprotnega dogodka:

.

Katero formulo uporabiti, je odvisno od tega, kateri od njih ima vsoto manj členov.

Značilnosti binomske porazdelitve se izračunajo z uporabo naslednjih formul .

Matematično pričakovanje: .

Razpršenost: .

Standardni odklon: .

Binomska porazdelitev in izračuni v MS Excelu

Binomska verjetnost p n( m) in vrednosti integralne funkcije F(m) lahko izračunate s funkcijo MS Excel BINOM.DIST. Spodaj je prikazano okno za ustrezen izračun (levi klik za povečavo).

MS Excel zahteva vnos naslednjih podatkov:

• število uspehov;
• število testov;
• verjetnost uspeha;
• integral - logična vrednost: 0 - če morate izračunati verjetnost p n( m) in 1 - če je verjetnost F(m).

Primer 1. Vodja podjetja je povzel podatke o številu prodanih kamer v zadnjih 100 dneh. V tabeli so povzeti podatki in izračunane verjetnosti, da bo določeno število kamer dnevno prodano.

Dan se konča z dobičkom, če se proda 13 ali več kamer. Verjetnost, da se bo dan končal z dobičkom:

Verjetnost, da bo dan opravljen brez dobička:

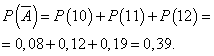
Naj bo verjetnost, da se dan dela z dobičkom, konstantna in enaka 0,61, število prodanih kamer na dan pa ni odvisno od dneva. Nato lahko uporabimo binomsko porazdelitev, kjer je dogodek A- dan bo opravljen z dobičkom, - brez dobička.

Verjetnost, da bo vseh 6 dni izpeljanih z dobičkom:

.

Enak rezultat dobimo s funkcijo MS Excel BINOM.DIST (vrednost integralne vrednosti je 0):

p 6 (6 ) = BINOM.DIST(6; 6; 0,61; 0) = 0,052.

Verjetnost, da bodo od 6 dni 4 ali več dni opravljeni z dobičkom:

kje ,

,

S pomočjo MS Excelove funkcije BINOM.DIST izračunamo verjetnost, da od 6 dni ne bomo več kot 3 dni zaključili z dobičkom (vrednost integralne vrednosti je 1):

p 6 (≤3 ) = BINOM.DIST(3; 6; 0,61; 1) = 0,435.

Verjetnost, da bo vseh 6 dni oddelanih z izgubami:

,

Isti indikator lahko izračunamo s pomočjo funkcije MS Excel BINOM.DIST:

p 6 (0 ) = BINOM.DIST(0; 6; 0,61; 0) = 0,0035.

Rešite težavo sami in nato poglejte rešitev

Primer 2. V žari sta 2 beli krogli in 3 črne krogle. Iz žare se vzame kroglica, barva se nastavi in ​​vrne nazaj. Poskus se ponovi 5-krat. Število pojavitev belih kroglic je diskretna naključna spremenljivka X, porazdeljeno po binomskem zakonu. Sestavite zakon porazdelitve naključne spremenljivke. Določite način, matematično pričakovanje in disperzijo.

Nadaljujmo z reševanjem težav skupaj

Primer 3. Iz kurirske službe smo šli na mesta n= 5 kurirjev. Vsak kurir je verjetno str= 0,3, ne glede na druge, zamuja za objekt. Diskretna naključna spremenljivka X- število zamudnih kurirjev. Konstruirajte porazdelitveni niz za to naključno spremenljivko. Poiščite njegovo matematično pričakovanje, varianco, standardni odklon. Poiščite verjetnost, da bosta vsaj dva kurirja zamudila na predmete.

Lep pozdrav vsem bralcem!

Statistična analiza se, kot vemo, ukvarja z zbiranjem in obdelavo realnih podatkov. Posel je uporaben in pogosto donosen, ker... pravilni sklepi vam omogočajo, da se izognete napakam in izgubam v prihodnosti in včasih pravilno ugibate prav to prihodnost. Zbrani podatki odražajo stanje nekega opazovanega pojava. Podatki so pogosto (vendar ne vedno) numerični in jih je mogoče matematično obdelati, da iz njih pridobimo dodatne informacije.

Niso pa vsi pojavi merjeni na kvantitativnem merilu kot je 1, 2, 3 ... 100500 ... Pojav ne more vedno zavzeti neskončnega ali velikega števila različnih stanj. Na primer, spol osebe je lahko M ali Ž. Strelec bodisi zadene tarčo bodisi zgreši. Glasujete lahko "za" ali "proti" itd. itd. Z drugimi besedami, takšni podatki odražajo stanje alternativnega atributa - bodisi "da" (dogodek se je zgodil) ali "ne" (dogodek se ni zgodil). Dogodek, ki se zgodi (pozitiven izid), se imenuje tudi "uspeh". Takšni pojavi so lahko tudi razširjeni in naključni. Zato jih je mogoče izmeriti in narediti statistično veljavne zaključke.

Poskusi s takimi podatki se imenujejo Bernoullijeva shema, v čast slavnega švicarskega matematika, ki je ugotovil, da se pri velikem številu poskusov razmerje med pozitivnimi rezultati in skupnim številom poskusov nagiba k verjetnosti pojava tega dogodka.

Alternativna značilna spremenljivka

Za uporabo matematičnega aparata pri analizi je treba rezultate takih opazovanj zapisati v numerični obliki. Da bi to naredili, je pozitivnemu izidu dodeljena številka 1, negativnemu izidu - 0. Z drugimi besedami, imamo opravka s spremenljivko, ki ima lahko le dve vrednosti: 0 ali 1.

Kakšne koristi lahko iz tega izvlečemo? Pravzaprav nič manj kot iz navadnih podatkov. Tako je enostavno izračunati število pozitivnih rezultatov - samo seštejte vse vrednosti, tj. vse 1 (uspeh). Lahko greste še dlje, vendar bo to zahtevalo uvedbo nekaj zapisov.

Prva stvar, ki jo je treba opozoriti, je, da obstaja določena verjetnost za pozitivne rezultate (ki so enaki 1). Na primer, pridobivanje glav pri metanju kovanca je ½ ali 0,5. To verjetnost tradicionalno označujemo z latinsko črko str. Zato je verjetnost, da se zgodi alternativni dogodek, enaka 1 - str, kar je tudi označeno z q, to je q = 1 – str. Te zapise je mogoče jasno sistematizirati v obliki tabele porazdelitve spremenljivk X.

Zdaj imamo seznam možnih vrednosti in njihove verjetnosti. Začnemo lahko izračunavati tako izjemne značilnosti naključne spremenljivke, kot je matematično pričakovanje in disperzija. Naj vas spomnim, da je matematično pričakovanje izračunano kot vsota produktov vseh možnih vrednosti in njihovih ustreznih verjetnosti:

Izračunajmo pričakovanje z uporabo zapisa v zgornjih tabelah.

Izkazalo se je, da je matematično pričakovanje alternativnega znaka enako verjetnosti tega dogodka - str.

Zdaj pa definirajmo, kaj je varianca alternativnega atributa. Naj vas še spomnim, da je disperzija povprečni kvadrat odstopanj od matematičnega pričakovanja. Splošna formula (za diskretne podatke) je:

Od tod varianca alternativnega atributa:

Lahko je videti, da ima ta disperzija največ 0,25 (s p=0,5).

Standardni odklon je koren variance:

Največja vrednost ne presega 0,5.

Kot lahko vidite, imata tako matematično pričakovanje kot varianca alternativnega atributa zelo kompaktno obliko.

Binomska porazdelitev naključne spremenljivke

Zdaj pa poglejmo situacijo z drugega zornega kota. Dejansko, koga briga, da je povprečna izguba glav na met 0,5? Nemogoče si je niti predstavljati. Bolj zanimivo je postaviti vprašanje o številu glav, ki se zgodijo pri določenem številu metov.

Z drugimi besedami, raziskovalca pogosto zanima verjetnost, da se zgodi določeno število uspešnih dogodkov. To je lahko število izdelkov z napako v testirani seriji (1 - z napako, 0 - dobro) ali število izterjatev (1 - zdravo, 0 - bolno) itd. Število takih "uspehov" bo enako vsoti vseh vrednosti spremenljivke X, tj. število posameznih rezultatov.

Naključna spremenljivka B se imenuje binom in ima vrednosti od 0 do n(pri B= 0 - vsi deli so primerni, z B = n– vsi deli so okvarjeni). Predpostavlja se, da vse vrednosti x neodvisni drug od drugega. Razmislimo o glavnih značilnostih binomske spremenljivke, to je, ugotovili bomo njeno matematično pričakovanje, disperzijo in porazdelitev.

Pričakovanje binomske spremenljivke je zelo enostavno dobiti. Naj spomnimo, da obstaja vsota matematičnih pričakovanj vsake dodane vrednosti in je za vse enaka, torej:

Na primer, matematično pričakovanje števila padlih glav v 100 metih je 100 × 0,5 = 50.

Zdaj pa izpeljimo formulo za disperzijo binomske spremenljivke. je vsota varianc. Od tukaj

Standardni odklon oz

Za 100 metov kovancev je standardna deviacija

Na koncu upoštevajte porazdelitev binomske vrednosti, tj. verjetnost, da naključna spremenljivka B bodo prevzele različne vrednosti k, Kje 0≤k≤n. Za kovanec bi ta problem lahko izgledal takole: Kakšna je verjetnost, da dobite 40 glav pri 100 metih?

Da bi razumeli metodo izračuna, si predstavljajte, da je kovanec vržen le 4-krat. Vsakič lahko izpade katera koli stran. Vprašamo se, kakšna je verjetnost, da dobimo 2 glavi od 4 metov. Vsak met je neodvisen drug od drugega. To pomeni, da bo verjetnost, da dobite katero koli kombinacijo, enaka produktu verjetnosti danega izida za vsak posamezen met. Naj bodo O glave in P repi. Potem lahko na primer ena od kombinacij, ki nam ustreza, izgleda kot OOPP, to je:

Verjetnost takšne kombinacije je enaka zmnožku dveh verjetnosti, da dobimo glave in še dveh verjetnosti, da ne dobimo glav (obraten dogodek, izračunan kot 1 - str), tj. 0,5×0,5×(1-0,5)×(1-0,5)=0,0625. To je verjetnost ene od kombinacij, ki nam ustreza. Toda vprašanje je bilo o skupnem številu orlov in ne o kakšnem posebnem vrstnem redu. Nato morate sešteti verjetnosti vseh kombinacij, v katerih sta točno 2 glavi. Jasno je, da so vsi enaki (zmnožek se ne spremeni, ko se faktorji spremenijo). Zato morate izračunati njihovo število in nato pomnožiti z verjetnostjo katere koli takšne kombinacije. Preštejmo vse kombinacije 4 metov 2 glav: RROO, RORO, ROOR, ORRO, OROR, OORR. Skupaj je na voljo 6 možnosti.

Zato je želena verjetnost, da dobite 2 glavi po 4 metih, 6×0,0625=0,375.

Vendar je štetje na ta način dolgočasno. Že za 10 kovancev bo zelo težko pridobiti skupno število možnosti s surovo silo. Zato so pametni ljudje že zdavnaj izumili formulo, s katero izračunajo število različnih kombinacij n elementi po k, Kje n– skupno število elementov, k– število elementov, katerih možnosti razporeditve se štejejo. Kombinacija formule n elementi po k je to:

Podobno se dogaja na oddelku kombinatorike. Tja pošljem vsakogar, ki želi izpopolniti svoje znanje. Od tod, mimogrede, ime binomske porazdelitve (zgornja formula je koeficient v razširitvi Newtonovega binoma).

Formulo za določanje verjetnosti je mogoče zlahka posplošiti na katero koli količino n in k. Posledično ima formula za binomsko porazdelitev naslednjo obliko.

Z besedami: število kombinacij, ki izpolnjujejo pogoj, pomnoženo z verjetnostjo ene od njih.

Za praktično uporabo je dovolj, da preprosto poznate formulo za binomsko porazdelitev. Morda pa sploh ne veste – spodaj prikazujemo, kako določiti verjetnost z uporabo Excela. Ampak bolje je vedeti.

S to formulo izračunamo verjetnost, da dobimo 40 glav v 100 metih:

Ali samo 1,08 %. Za primerjavo, verjetnost matematičnega pričakovanja tega poskusa, to je 50 glav, je enaka 7,96%. Največja verjetnost binomske vrednosti pripada vrednosti, ki ustreza matematičnemu pričakovanju.

Izračun verjetnosti binomske porazdelitve v Excelu

Če uporabljate samo papir in kalkulator, so izračuni z binomsko porazdelitveno formulo kljub odsotnosti integralov precej težavni. Na primer, vrednost je 100! – ima več kot 150 znakov. Tega je nemogoče izračunati ročno. Prej in tudi zdaj so za izračun takšnih količin uporabljali približne formule. Trenutno je priporočljivo uporabljati posebno programsko opremo, kot je MS Excel. Tako lahko vsak uporabnik (tudi humanist po izobrazbi) enostavno izračuna verjetnost vrednosti binomsko porazdeljene naključne spremenljivke.

Za utrjevanje snovi bomo Excel za zdaj uporabljali kot običajen kalkulator, t.j. Izvedimo izračun po korakih z uporabo formule binomske porazdelitve. Izračunajmo na primer verjetnost, da dobimo 50 glav. Spodaj je slika s koraki izračuna in končnim rezultatom.

Kot lahko vidite, so vmesni rezultati takšnega obsega, da se ne prilegajo v celico, čeprav preproste funkcije, kot so FACTOR (izračun faktorijela), POWER (povečanje števila na potenco), pa tudi množenje in deljenje operaterji se uporabljajo povsod. Poleg tega je ta izračun precej okoren; v vsakem primeru ni kompakten, ker vključenih je veliko celic. Da, in to je malo težko takoj ugotoviti.

Na splošno Excel ponuja že pripravljeno funkcijo za izračun verjetnosti binomske porazdelitve. Funkcija se imenuje BINOM.DIST.

Število uspehov– število uspešnih testov. Imamo jih 50.

Število testov– število metov: 100-krat.

Verjetnost uspeha– verjetnost, da dobite glave v enem metu, je 0,5.

Integral– prikazana je 1 ali 0. Če je 0, se izračuna verjetnost P(B=k); če je 1, se izračuna funkcija binomske porazdelitve, tj. vsota vseh verjetnosti iz B=0 do B=k vključno.

Kliknite V redu in dobite enak rezultat kot zgoraj, le da je vse izračunala ena funkcija.

Zelo priročno. Za eksperimentiranje namesto zadnjega parametra 0 damo 1. Dobimo 0,5398. To pomeni, da je pri 100 metih kovancev verjetnost, da dobite glave med 0 in 50, skoraj 54 %. Toda sprva se je zdelo, da bi moralo biti 50%. Na splošno so izračuni narejeni hitro in enostavno.

Pravi analitik mora razumeti, kako se funkcija obnaša (kakšna je njena porazdelitev), zato bomo izračunali verjetnosti za vse vrednosti od 0 do 100. To pomeni, postavili bomo vprašanje: kakšna je verjetnost, da niti ena glava se bo prikazal, da se bo pojavil 1 orel, 2, 3, 50, 90 ali 100. Izračun je prikazan na naslednji samogibljivi sliki. Modra črta je sama binomska porazdelitev, rdeča pika je verjetnost za določeno število uspehov k.

Nekdo bi lahko vprašal, ali je binomska porazdelitev podobna ... Da, zelo podobna. Že Moivre (leta 1733) je rekel, da se približuje binomska porazdelitev z velikimi vzorci (ne vem, kako se je takrat reklo), a ga nihče ni poslušal. Šele Gauss in nato Laplace 60-70 let pozneje sta ponovno odkrila in skrbno preučila zakon normalne porazdelitve. Zgornji graf jasno kaže, da največja verjetnost pade na matematično pričakovanje, z odstopanjem od njega pa se močno zmanjša. Tako kot običajni zakon.

Binomska porazdelitev je zelo praktičnega pomena in se pojavlja precej pogosto. Z uporabo Excela se izračuni izvedejo hitro in enostavno. Tako ga lahko varno uporabljate.

S tem predlagam, da se poslovimo do naslednjega srečanja. Vse dobro, ostanite zdravi!

pozdravljena Že vemo, kaj je porazdelitev verjetnosti. Tisti. verjetnost vsake od teh situacij je 1/32. Zdaj so ostali še 4 meti, kar pomeni, da lahko druge "glave" padejo na enega od 4 metov. To je 3! Tukaj je bilo 5 takih metod od 32. Tukaj - 10 od 32. Kljub temu smo izvedli izračune in zdaj smo pripravljeni narisati porazdelitev verjetnosti.