Промежутки возрастания и убывания функции онлайн. Возрастание, убывание и экстремумы функции

1. Найти область определения функции

2.Найти производную функции

3. Приравнять производную к нулю и найти критические точки функции

4. Отметить критические точки на области определения

5. Вычислить знак производной в каждом из полученных интервалов

6. Выяснить поведение функции в каждом интервале.

Пример: Найдите промежутки возрастания и убывания функции f (x ) = и число нулей данной функции на промежутке .

Решение:

1. D(f ) = R

2. f "(x ) =

D(f ") = D(f ) = R

3. Найдём критические точки функции, решив уравнение f "(x ) = 0.

x (x – 10) = 0

критические точки функции x = 0 и x = 10.

4. Определим знак производной.

f "(x ) + – +

f (x ) 0 10 x

в промежутках (-∞; 0) и (10; +∞) производная функции положительна и в точках x = 0 и x = 10 функция f (x ) непрерывна, следовательно, данная функция возрастает на промежутках: (-∞; 0]; .

Определим знак значений функции на концах отрезка.

f (0) = 3, f (0) > 0

f (10) = , f (10) < 0.

Так как на отрезке функция убывает и знак значений функции изменяется, то на этом отрезке один нуль функции.

Ответ: функция f(x) возрастает на промежутках: (-∞; 0]; ;

на промежутке функция имеет один нуль функции.

2. Точки экстремума функции: точки максимума и точки минимума. Необходимое и достаточное условия существования экстремума функции. Правило исследования функции на экстремум .

Определение 1: Точки, в которых производная равна нулю, называются критическими или стационарными.

Определение 2 . Точка называется точкой минимума (максимума) функции , если значение функции в этой точке меньше (больше) ближайших значений функии.

Следует иметь в виду, что максимум и минимум в данном случае являются локальными.

На рис. 1. изображены локальные максимумы и минимумы.

Теорема 1. (необходимый признак существования экстремума функции). Если дифференцируемая в точке функция имеет в этой точке максимум или минимум, то ее производная при обращается в нуль, .

Теорема 2. (достаточный признак существования экстремума функции). Если непрерывная функция имеет производную во всех точках некоторого интервала, содержащего критическую точку (за исключением может быть самой этой точки), и если производная при переходе аргумента слева направо через критическую точку меняет знак с плюса на минус, то функция в этой точке имеет максимум, а при переходе знака с минуса на плюс – минимум.

Здравствуйте! Ударим по приближающемуся ЕГЭ качественной систематической подготовкой, и упорством в измельчении гранита науки!!! В конце поста имеется конкурсная задача, будьте первым! В одной из статей данной рубрики мы с вами , в которых был дан график функции, и ставились различные вопросы, касающиеся экстремумов, промежутков возрастания (убывания) и прочие.

В этой статье рассмотрим задачи входящие в ЕГЭ по математике, в которых дан график производной функции, и ставятся следующие вопросы:

1. В какой точке заданного отрезка функция принимает наибольшее (или наименьшее) значение.

2. Найти количество точек максимума (или минимума) функции, принадлежащих заданному отрезку.

3. Найти количество точек экстремума функции, принадлежащих заданному отрезку.

4. Найти точку экстремума функции, принадлежащую заданному отрезку.

5. Найти промежутки возрастания (или убывания) функции и в ответе указать сумму целых точек, входящих в эти промежутки.

6. Найти промежутки возрастания (или убывания) функции. В ответе указать длину наибольшего из этих промежутков.

7. Найти количество точек, в которых касательная к графику функции параллельна прямой вида у = kx + b или совпадает с ней.

8. Найти абсциссу точки, в которой касательная к графику функции параллельна оси абсцисс или совпадает с ней.

Могут стоять и другие вопросы, но они не вызовут у вас затруднений, если вы поняли и (ссылки указаны на статьи, в которых представлена необходимая для решения информация, рекомендую повторить).

Основная информация (кратко):

1. Производная на интервалах возрастания имеет положительный знак.

Если производная в определённой точке из некоторого интервала имеет положительное значение, то график функции на этом интервале возрастает.

2. На интервалах убывания производная имеет отрицательный знак.

Если производная в определённой точке из некоторого интервала имеет отрицательное значение, то график функции на этом интервале убывает.

3. Производная в точке х равна угловому коэффициенту касательной, проведённой к графику функции в этой же точке.

4. В точках экстремума (максимума-минимума) функции производная равна нулю. Касательная к графику функции в этой точке параллельна оси ох.

Это нужно чётко уяснить и помнить!!!

Многих график производной «смущает». Некоторые по невнимательности принимают его за график самой функции. Поэтому в таких зданиях, где видите, что дан график, сразу же акцентируйте своё внимание в условии на том, что дано: график функции или график производной функции?

Если это график производной функции, то относитесь к нему как бы к «отражению» самой функции, которое просто даёт вам информацию об этой функции.

Рассмотрим задание:

На рисунке изображен график у = f ′(х) - производной функции f (х) , определенной на интервале (–2;21).

Ответим на следующие вопросы:

1. В какой точке отрезка функция f (х) принимает наибольшее значение.

На заданном отрезке производная функции отрицательна, значит функция на этом отрезке убывает (она убывает от левой границы интервала к правой). Таким образом, наибольшее значение функции достигается на левой границе отрезка, т. е. в точке 7.

Ответ: 7

2. В какой точке отрезка функция f (х)

По данному графику производной можем сказать следующее. На заданном отрезке производная функции положительна, значит функция на этом отрезке возрастает (она возрастает от левой границы интервала к правой). Таким образом, наименьшее значение функции достигается на левой границе отрезка, то есть в точке х = 3.

Ответ: 3

3. Найдите количество точек максимума функции f (х)

Точки максимума соответствуют точкам смены знака производной с положительного на отрицательный. Рассмотрим, где таким образом меняется знак.

На отрезке (3;6) производная положительна, на отрезке (6;16) отрицательна.

На отрезке (16;18) производная положительна, на отрезке (18;20) отрицательна.

Таким образом, на заданном отрезке функция имеет две точки максимума х = 6 и х = 18.

Ответ: 2

4. Найдите количество точек минимума функции f (х) , принадлежащих отрезку .

Точки минимума соответствуют точкам смены знака производной с отрицательного на положительный. У нас на интервале (0;3) производная отрицательна, на интервале (3;4) положительна.

Таким образом, на отрезке функция имеет только одну точку минимума х = 3.

*Будьте внимательны при записи ответа – записывается количество точек, а не значение х, такую ошибку можно допустит из-за невнимательности.

Ответ: 1

5. Найдите количество точек экстремума функции f (х) , принадлежащих отрезку .

Обратите внимание, что необходимо найти количество точек экстремума (это и точки максимума и точки минимума).

Точки экстремума соответствуют точкам смены знака производной (с положительного на отрицательный или наоборот). На данном в условии графике это нули функции. Производная обращается в нуль в точках 3, 6, 16, 18.

Таким образом, на отрезке функция имеет 4 точки экстремума.

Ответ: 4

6. Найдите промежутки возрастания функции f (х)

Промежутки возрастания данной функции f (х) соответствуют промежуткам, на которых ее производная положительна, то есть интервалам (3;6) и (16;18). Обратите внимание, что границы интервала не входят в него (круглые скобки – границы не включены в интервал, квадратные – включены). Данные интервалы содержат целые точки 4, 5, 17. Их сумма равна: 4 + 5 + 17 = 26

Ответ: 26

7. Найдите промежутки убывания функции f (х) на заданном интервале. В ответе укажите сумму целых точек, входящих в эти промежутки.

Промежутки убывания функции f (х) соответствуют промежуткам, на которых производная функции отрицательна. В данной задаче это интервалы (–2;3), (6;16), (18;21).

Данные интервалы содержат следующие целые точки: –1, 0, 1, 2, 7, 8, 9, 10, 11, 12, 13, 14, 15, 19, 20. Их сумма равна:

(–1) + 0 + 1 + 2 + 7 + 8 + 9 + 10 +

11 + 12 + 13 + 14 + 15 + 19 + 20 = 140

Ответ: 140

*Обращайте внимание в условии: включены ли границы в интервал или нет. Если границы будут включены, то и в рассматриваемых в процессе решения интервалах эти границы также необходимо учитывать.

8. Найдите промежутки возрастания функции f (х)

Промежутки возрастания функции f (х) соответствуют промежуткам, на которых производная функции положительна. Мы уже указывали их: (3;6) и (16;18). Наибольшим из них является интервал (3;6), его длина равна 3.

Ответ: 3

9. Найдите промежутки убывания функции f (х) . В ответе укажите длину наибольшего из них.

Промежутки убывания функции f (х) соответствуют промежуткам, на которых производная функции отрицательна. Мы уже указывали их, это интервалы (–2;3), (6;16), (18;21), их длины соответственно равны 5, 10, 3.

Длина наибольшего равна 10.

Ответ: 10

10. Найдите количество точек, в которых касательная к графику функции f (х) параллельна прямой у = 2х + 3 или совпадает с ней.

Значение производной в точке касания равно угловому коэффициенту касательной. Так как касательная параллельна прямой у = 2х + 3 или совпадает с ней, то их угловые коэффициенты равны 2. Значит, необходимо найти количество точек, в которых у′(х 0) = 2. Геометрически это соответствует количеству точек пересечения графика производной с прямой у = 2. На данном интервале таких точек 4.

Ответ: 4

11. Найдите точку экстремума функции f (х) , принадлежащую отрезку .

Точка экстремума функции это такая точка, в которой её производная равна нулю, при чём в окрестности этой точки производная меняет знак (с положительного на отрицательный или наоборот). На отрезке график производной пересекает ось абсцисс, производная меняет знак с отрицательного на положительный. Следовательно, точка х = 3 является точкой экстремума.

Ответ: 3

12. Найдите абсциссы точек, в которых касательные к графику у = f (x) параллельны оси абсцисс или совпадают с ней. В ответе укажите наибольшую из них.

Касательная к графику у = f (x) может быть параллельна оси абсцисс или совпадать с ней, только в точках, где производная равна нулю (это могут быть точки экстремума или стационарные точки, в окрестностях которых производная свой знак не меняет). По данному графику видно, что производная равна нулю в точках 3, 6, 16,18. Наибольшая равна 18.

Можно построить рассуждение таким образом:

Значение производной в точке касания равно угловому коэффициенту касательной. Поскольку касательная параллельна оси абсцисс или совпадает с ней, её угловой коэффициент равен 0 (действительно тангенс угла в ноль градусов равен нулю). Следовательно, мы ищем точку, в которой угловой коэффициент, равен нулю, а значит, и производная равна нулю. Производная равна нулю в той точке, в которой её график пересекает ось абсцисс, а это точки 3, 6, 16,18.

Ответ: 18

На рисунке изображен график у = f ′(х) - производной функции f (х) , определенной на интервале (–8;4). В какой точке отрезка [–7;–3] функция f (х) принимает наименьшее значение.

На рисунке изображен график у = f ′(х) - производной функции f (х) , определенной на интервале (–7;14). Найдите количество точек максимума функции f (х) , принадлежащих отрезку [–6;9].

На рисунке изображен график у = f ′(х) - производной функции f (х) , определенной на интервале (–18;6). Найдите количество точек минимума функции f (х) , принадлежащих отрезку [–13;1].

На рисунке изображен график у = f ′(х) - производной функции f (х) , определенной на интервале (–11; –11). Найдите количество точек экстремума функции f (х) , принадлежащих отрезку [–10; –10].

На рисунке изображен график у = f ′(х) - производной функции f (х) , определенной на интервале (–7;4). Найдите промежутки возрастания функции f (х) . В ответе укажите сумму целых точек, входящих в эти промежутки.

На рисунке изображен график у = f ′(х) - производной функции f (х) , определенной на интервале (–5;7). Найдите промежутки убывания функции f (х) . В ответе укажите сумму целых точек, входящих в эти промежутки.

На рисунке изображен график у = f ′(х) - производной функции f (х) , определенной на интервале (–11;3). Найдите промежутки возрастания функции f (х) . В ответе укажите длину наибольшего из них.

F На рисунке изображен график

Условие задачи то же (которую мы рассматривали). Найдите сумму трёх чисел:

1. Сумма квадратов экстремумов функции f (х).

2. Разность квадратов суммы точек максимума и суммы точек минимума функции f (х).

3. Количество касательных к f (х), параллельных прямой у = –3х + 5.

Первый, кто даст верный ответ, получит поощрительный приз – 150 рублей. Ответы пишите в комментариях. Если это ваш первый комментарий на блоге, то сразу он не появится, чуть позже (не беспокойтесь, время написания комментария регистрируется).

Успеха вам!

С уважением, Александр Крутицих.

P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.

Возрастание и убывание функции

функция y = f (x ) называется возрастающей на отрезке [a , b ], если для любой пары точек х и х" , а ≤ х выполняется неравенство f (x ) ≤ f (x" ), и строго возрастающей - если выполняется неравенство f (x ) f (x" ). Аналогично определяется убывание и строгое убывание функции. Например, функция у = х 2 (рис. , а) строго возрастает на отрезке , а

(рис. , б) строго убывает на этом отрезке. Возрастающие функции обозначаются f (x ), а убывающие f (x )↓. Для того чтобы дифференцируемая функция f (x ) была возрастающей на отрезке [а , b ], необходимо и достаточно, чтобы её производная f "(x ) была неотрицательной на [а , b ].

Наряду с возрастанием и убыванием функции на отрезке рассматривают возрастание и убывание функции в точке. Функция у = f (x ) называется возрастающей в точке x 0 , если найдётся такой интервал (α, β), содержащий точку x 0 , что для любой точки х из (α, β), х> x 0 , выполняется неравенство f (x 0) ≤ f (x ), и для любой точки х из (α, β), х 0 , выполняется неравенство f (x ) ≤ f (x 0). Аналогично определяется строгое возрастание функции в точке x 0 . Если f "(x 0) > 0, то функция f (x ) строго возрастает в точке x 0 . Если f (x ) возрастает в каждой точке интервала (a , b ), то она возрастает на этом интервале.

С. Б. Стечкин.

Большая советская энциклопедия. - М.: Советская энциклопедия . 1969-1978 .

Смотреть что такое "Возрастание и убывание функции" в других словарях:

Понятия математического анализа. Функция f(x) называется возрастающей на отрезке ВОЗРАСТНАЯ СТРУКТУРА НАСЕЛЕНИЯ соотношение численности разных возрастных групп населения. Зависит от уровней рождаемости и смертности, продолжительности жизни людей … Большой Энциклопедический словарь

Понятия математического анализа. Функция f(х) называется возрастающей на отрезке , если для любой пары точек x1 и x2, a≤x1 … Энциклопедический словарь

Понятия матем. анализа. Ф ция f(x) наз. возрастающей на отрезке [а, b], если для любой пары точек х1 и x2, а<или=х1 <х<или=b, выполняется неравенство f(x1)Естествознание. Энциклопедический словарь

Раздел математики, в котором изучаются производные и дифференциалы функций и их применения к исследованию функций. Оформление Д. и. в самостоятельную математическую дисциплину связано с именами И. Ньютона и Г. Лейбница (вторая половина 17 … Большая советская энциклопедия

Раздел математики, в к ром изучаются понятия производной и дифференциала и способы их применения к исследованию функций. Развитие Д. и. тесно связано с развитием интегрального исчисления. Неразрывно и их содержание. Вместе они составляют основу… … Математическая энциклопедия

У этого термина существуют и другие значения, см. функция. Запрос «Отображение» перенаправляется сюда; см. также другие значения … Википедия

Аристотель и перипатетики - Аристотелевский вопрос Жизнь Аристотеля Аристотель родился в 384/383 гг. до н. э. в Стагире, на границе с Македонией. Его отец по имени Никомах был врачом на службе у македонского царя Аминта, отца Филиппа. Вместе с семьей молодой Аристотель… … Западная философия от истоков до наших дней

- (КХД), квантовополевая теория сильного вз ствия кварков и глюонов, построенная по образу квант. электродинамики (КЭД) на основе «цветовой» калибровочной симметрии. В отличие от КЭД, фермионы в КХД имеют дополнит. степень свободы квант. число,… … Физическая энциклопедия

I Сердце Сердце (лат. соr, греч. cardia) полый фиброзно мышечный орган, который, функционируя как насос, обеспечивает движение крови а системе кровообращения. Анатомия Сердце находится в переднем средостении (Средостение) в Перикарде между… … Медицинская энциклопедия

Жизнь растения, как и всякого другого живого организма, представляет сложную совокупность взаимосвязанных процессов; наиболее существенный из них, как известно, обмен веществ с окружающей средой. Среда является тем источником, откуда… … Биологическая энциклопедия

Экстремумы функции

Определение 2

Точка $x_0$ называется точкой максимума функции $f(x)$, если существует такая окрестность данной точки, что для всех $x$ из этой окрестность выполняется неравенство $f(x)\le f(x_0)$.

Определение 3

Точка $x_0$ называется точкой максимума функции $f(x)$, если существует такая окрестность данной точки, что для всех $x$ из этой окрестность выполняется неравенство $f(x)\ge f(x_0)$.

Понятие экстремума функции тесно связано с понятием критической точки функции. Введем её определение.

Определение 4

$x_0$ называется критической точкой функции $f(x)$, если:

1) $x_0$ - внутренняя точка области определения;

2) $f"\left(x_0\right)=0$ или не существует.

Для понятия экстремума можно сформулировать теоремы о достаточных и необходимых условиях его существования.

Теорема 2

Достаточное условие экстремума

Пусть точка $x_0$ является критической для функции $y=f(x)$ и лежит в интервале $(a,b)$. Пусть на каждом интервале $\left(a,x_0\right)\ и\ (x_0,b)$ производная $f"(x)$ существует и сохраняет постоянный знак. Тогда:

1) Если на интервале $(a,x_0)$ производная $f"\left(x\right)>0$, а на интервале $(x_0,b)$ производная $f"\left(x\right)

2) Если на интервале $(a,x_0)$ производная $f"\left(x\right)0$, то точка $x_0$ - точка минимума для данной функции.

3) Если и на интервале $(a,x_0)$, и на интервале $(x_0,b)$ производная $f"\left(x\right) >0$ или производная $f"\left(x\right)

Данная теорема проиллюстрирована на рисунке 1.

Рисунок 1. Достаточное условие существования экстремумов

Примеры экстремумов (Рис. 2).

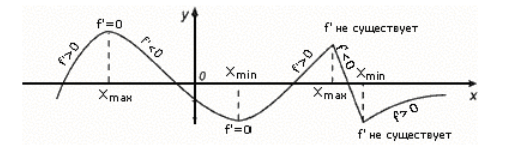
Рисунок 2. Примеры точек экстремумов

Правило исследования функции на экстремум

2) Найти производную $f"(x)$;

7) Сделать выводы о наличии максимумов и минимумов на каждом промежутке, используя теорему 2.

Возрастание и убывание функции

Введем, для начала, определения возрастающей и убывающей функций.

Определение 5

Функция $y=f(x)$, определенная на промежутке $X$, называется возрастающей, если для любых точек $x_1,x_2\in X$ при $x_1

Определение 6

Функция $y=f(x)$, определенная на промежутке $X$, называется убывающей, если для любых точек $x_1,x_2\in X$ при $x_1f(x_2)$.

Исследование функции на возрастание и убывание

Исследовать функции на возрастание и убывание можно с помощью производной.

Для того чтобы исследовать функцию на промежутки возрастания и убывания, необходимо сделать следующее:

1) Найти область определения функции $f(x)$;

2) Найти производную $f"(x)$;

3) Найти точки, в которых выполняется равенство $f"\left(x\right)=0$;

4) Найти точки, в которых $f"(x)$ не существует;

5) Отметить на координатной прямой все найденные точки и область определения данной функции;

6) Определить знак производной $f"(x)$ на каждом получившемся промежутке;

7) Сделать вывод: на промежутках, где $f"\left(x\right)0$ функция возрастает.

Примеры задач на исследования функций на возрастание, убывание и наличие точек экстремумов

Пример 1

Исследовать функцию на возрастание и убывание, и наличие точек максимумов и минимумов: $f(x)={2x}^3-15x^2+36x+1$

Так как первые 6 пунктов совпадают, проведем для начала их.

1) Область определения - все действительные числа;

2) $f"\left(x\right)=6x^2-30x+36$;

3) $f"\left(x\right)=0$;

\ \ \

4) $f"(x)$ существует во всех точках области определения;

5) Координатная прямая:

Рисунок 3.

6) Определить знак производной $f"(x)$ на каждом промежутке:

\ \ . Оно находится при помощи точек максимума и равняется максимальному значению функции, а второй рисунок больше походит на поиск точки максимума при х = b .

Достаточные условия возрастания и убывания функции

Чтобы найти максимумы и минимумы функции, необходимо применять признаки экстремума в том случае, когда функция удовлетворяет этим условиям. Самым часто используемым считается первый признак.

Первое достаточное условие экстремума

Пусть задана функция y = f (x) , которая дифференцируема в ε окрестности точки x 0 , причем имеет непрерывность в заданной точке x 0 . Отсюда получаем, что

• когда f " (x) > 0 с x ∈ (x 0 - ε ; x 0) и f " (x) < 0 при x ∈ (x 0 ; x 0 + ε) , тогда x 0 является точкой максимума;
• когда f " (x) < 0 с x ∈ (x 0 - ε ; x 0) и f " (x) > 0 при x ∈ (x 0 ; x 0 + ε) , тогда x 0 является точкой минимума.

Иначе говоря, получим их условия постановки знака:

• когда функция непрерывна в точке x 0 , тогда имеет производную с меняющимся знаком, то есть с + на - , значит, точка называется максимумом;
• когда функция непрерывна в точке x 0 , тогда имеет производную с меняющимся знаком с - на + , значит, точка называется минимумом.

Чтобы верно определить точки максимума и минимума функции, необходимо следовать алгоритму их нахождения:

• найти область определения;
• найти производную функции на этой области;
• определить нули и точки, где функция не существует;
• определение знака производной на интервалах;
• выбрать точки, где функция меняет знак.

Рассмотрим алгоритм на примере решения нескольких примеров на нахождение экстремумов функции.

Пример 1

Найти точки максимума и минимума заданной функции y = 2 (x + 1) 2 x - 2 .

Решение

Область определения данной функции – это все действительные числа кроме х = 2 . Для начала найдем производную функции и получим:

y " = 2 x + 1 2 x - 2 " = 2 · x + 1 2 " · (x - 2) - (x + 1) 2 · (x - 2) " (x - 2) 2 = = 2 · 2 · (x + 1) · (x + 1) " · (x - 2) - (x + 1) 2 · 1 (x - 2) 2 = 2 · 2 · (x + 1) · (x - 2) - (x + 2) 2 (x - 2) 2 = = 2 · (x + 1) · (x - 5) (x - 2) 2

Отсюда видим, что нули функции – это х = - 1 , х = 5 , х = 2 , то есть каждую скобку необходимо приравнять к нулю. Отметим на числовой оси и получим:

Теперь определим знаки производной из каждого интервала. Необходимо выбрать точку, входящую в интервал, подставить в выражение. Например, точки х = - 2 , х = 0 , х = 3 , х = 6 .

Получаем, что

y " (- 2) = 2 · (x + 1) · (x - 5) (x - 2) 2 x = - 2 = 2 · (- 2 + 1) · (- 2 - 5) (- 2 - 2) 2 = 2 · 7 16 = 7 8 > 0 , значит, интервал - ∞ ; - 1 имеет положительную производную. Аналогичным образом получаем, что

y " (0) = 2 · (0 + 1) · 0 - 5 0 - 2 2 = 2 · - 5 4 = - 5 2 < 0 y " (3) = 2 · (3 + 1) · (3 - 5) (3 - 2) 2 = 2 · - 8 1 = - 16 < 0 y " (6) = 2 · (6 + 1) · (6 - 5) (6 - 2) 2 = 2 · 7 16 = 7 8 > 0

Так как второй интервал получился меньше нуля, значит, производная на отрезке будет отрицательной. Третий с минусом, четвертый с плюсом. Для определения непрерывности необходимо обратить внимание на знак производной, если он меняется, тогда это точка экстремума.

Получим, что в точке х = - 1 функция будет непрерывна, значит, производная изменит знак с + на - . По первому признаку имеем, что х = - 1 является точкой максимума, значит получаем

y m a x = y (- 1) = 2 · (x + 1) 2 x - 2 x = - 1 = 2 · (- 1 + 1) 2 - 1 - 2 = 0

Точка х = 5 указывает на то, что функция является непрерывной, а производная поменяет знак с – на +. Значит, х=-1 является точкой минимума, причем ее нахождение имеет вид

y m i n = y (5) = 2 · (x + 1) 2 x - 2 x = 5 = 2 · (5 + 1) 2 5 - 2 = 24

Графическое изображение

Ответ: y m a x = y (- 1) = 0 , y m i n = y (5) = 24 .

Стоит обратить внимание на то, что использование первого достаточного признака экстремума не требует дифференцируемости функции с точке x 0 , этим и упрощает вычисление.

Пример 2

Найти точки максимума и минимума функции y = 1 6 x 3 = 2 x 2 + 22 3 x - 8 .

Решение.

Область определения функции – это все действительные числа. Это можно записать в виде системы уравнений вида:

1 6 x 3 - 2 x 2 - 22 3 x - 8 , x < 0 1 6 x 3 - 2 x 2 + 22 3 x - 8 , x ≥ 0

После чего необходимо найти производную:

y " = 1 6 x 3 - 2 x 2 - 22 3 x - 8 " , x < 0 1 6 x 3 - 2 x 2 + 22 3 x - 8 " , x > 0 y " = - 1 2 x 2 - 4 x - 22 3 , x < 0 1 2 x 2 - 4 x + 22 3 , x > 0

Точка х = 0 не имеет производной, потому как значения односторонних пределов разные. Получим, что:

lim y " x → 0 - 0 = lim y x → 0 - 0 - 1 2 x 2 - 4 x - 22 3 = - 1 2 · (0 - 0) 2 - 4 · (0 - 0) - 22 3 = - 22 3 lim y " x → 0 + 0 = lim y x → 0 - 0 1 2 x 2 - 4 x + 22 3 = 1 2 · (0 + 0) 2 - 4 · (0 + 0) + 22 3 = + 22 3

Отсюда следует, что функция непрерывна в точке х = 0 , тогда вычисляем

lim y x → 0 - 0 = lim x → 0 - 0 - 1 6 x 3 - 2 x 2 - 22 3 x - 8 = = - 1 6 · (0 - 0) 3 - 2 · (0 - 0) 2 - 22 3 · (0 - 0) - 8 = - 8 lim y x → 0 + 0 = lim x → 0 - 0 1 6 x 3 - 2 x 2 + 22 3 x - 8 = = 1 6 · (0 + 0) 3 - 2 · (0 + 0) 2 + 22 3 · (0 + 0) - 8 = - 8 y (0) = 1 6 x 3 - 2 x 2 + 22 3 x - 8 x = 0 = 1 6 · 0 3 - 2 · 0 2 + 22 3 · 0 - 8 = - 8

Необходимо произвести вычисления для нахождения значения аргумента, когда производная становится равной нулю:

1 2 x 2 - 4 x - 22 3 , x < 0 D = (- 4) 2 - 4 · - 1 2 · - 22 3 = 4 3 x 1 = 4 + 4 3 2 · - 1 2 = - 4 - 2 3 3 < 0 x 2 = 4 - 4 3 2 · - 1 2 = - 4 + 2 3 3 < 0

1 2 x 2 - 4 x + 22 3 , x > 0 D = (- 4) 2 - 4 · 1 2 · 22 3 = 4 3 x 3 = 4 + 4 3 2 · 1 2 = 4 + 2 3 3 > 0 x 4 = 4 - 4 3 2 · 1 2 = 4 - 2 3 3 > 0

Все полученные точки нужно отметить на прямой для определения знака каждого интервала. Поэтому необходимо вычислить производную в произвольных точках у каждого интервала. Например, у нас можно взять точки со значениями x = - 6 , x = - 4 , x = - 1 , x = 1 , x = 4 , x = 6 . Получим, что

y " (- 6) = - 1 2 x 2 - 4 x - 22 3 x = - 6 = - 1 2 · - 6 2 - 4 · (- 6) - 22 3 = - 4 3 < 0 y " (- 4) = - 1 2 x 2 - 4 x - 22 3 x = - 4 = - 1 2 · (- 4) 2 - 4 · (- 4) - 22 3 = 2 3 > 0 y " (- 1) = - 1 2 x 2 - 4 x - 22 3 x = - 1 = - 1 2 · (- 1) 2 - 4 · (- 1) - 22 3 = 23 6 < 0 y " (1) = 1 2 x 2 - 4 x + 22 3 x = 1 = 1 2 · 1 2 - 4 · 1 + 22 3 = 23 6 > 0 y " (4) = 1 2 x 2 - 4 x + 22 3 x = 4 = 1 2 · 4 2 - 4 · 4 + 22 3 = - 2 3 < 0 y " (6) = 1 2 x 2 - 4 x + 22 3 x = 6 = 1 2 · 6 2 - 4 · 6 + 22 3 = 4 3 > 0

Изображение на прямой имеет вид

Значит, приходим к тому, что необходимо прибегнуть к первому признаку экстремума. Вычислим и получим, что

x = - 4 - 2 3 3 , x = 0 , x = 4 + 2 3 3 , тогда отсюда точки максимума имеют значени x = - 4 + 2 3 3 , x = 4 - 2 3 3

Перейдем к вычислению минимумов:

y m i n = y - 4 - 2 3 3 = 1 6 x 3 - 2 2 + 22 3 x - 8 x = - 4 - 2 3 3 = - 8 27 3 y m i n = y (0) = 1 6 x 3 - 2 2 + 22 3 x - 8 x = 0 = - 8 y m i n = y 4 + 2 3 3 = 1 6 x 3 - 2 2 + 22 3 x - 8 x = 4 + 2 3 3 = - 8 27 3

Произведем вычисления максимумов функции. Получим, что

y m a x = y - 4 + 2 3 3 = 1 6 x 3 - 2 2 + 22 3 x - 8 x = - 4 + 2 3 3 = 8 27 3 y m a x = y 4 - 2 3 3 = 1 6 x 3 - 2 2 + 22 3 x - 8 x = 4 - 2 3 3 = 8 27 3

Графическое изображение

Ответ:

y m i n = y - 4 - 2 3 3 = - 8 27 3 y m i n = y (0) = - 8 y m i n = y 4 + 2 3 3 = - 8 27 3 y m a x = y - 4 + 2 3 3 = 8 27 3 y m a x = y 4 - 2 3 3 = 8 27 3

Если задана функция f " (x 0) = 0 , тогда при ее f "" (x 0) > 0 получаем, что x 0 является точкой минимума, если f "" (x 0) < 0 , то точкой максимума. Признак связан с нахождением производной в точке x 0 .

Пример 3

Найти максимумы и минимумы функции y = 8 x x + 1 .

Решение

Для начала находим область определения. Получаем, что

D (y) : x ≥ 0 x ≠ - 1 ⇔ x ≥ 0

Необходимо продифференцировать функцию, после чего получим

y " = 8 x x + 1 " = 8 · x " · (x + 1) - x · (x + 1) " (x + 1) 2 = = 8 · 1 2 x · (x + 1) - x · 1 (x + 1) 2 = 4 · x + 1 - 2 x (x + 1) 2 · x = 4 · - x + 1 (x + 1) 2 · x

При х = 1 производная становится равной нулю, значит, точка является возможным экстремумом. Для уточнения необходимо найти вторую производную и вычислить значение при х = 1 . Получаем:

y "" = 4 · - x + 1 (x + 1) 2 · x " = = 4 · (- x + 1) " · (x + 1) 2 · x - (- x + 1) · x + 1 2 · x " (x + 1) 4 · x = = 4 · (- 1) · (x + 1) 2 · x - (- x + 1) · x + 1 2 " · x + (x + 1) 2 · x " (x + 1) 4 · x = = 4 · - (x + 1) 2 x - (- x + 1) · 2 x + 1 (x + 1) " x + (x + 1) 2 2 x (x + 1) 4 · x = = - (x + 1) 2 x - (- x + 1) · x + 1 · 2 x + x + 1 2 x (x + 1) 4 · x = = 2 · 3 x 2 - 6 x - 1 x + 1 3 · x 3 ⇒ y "" (1) = 2 · 3 · 1 2 - 6 · 1 - 1 (1 + 1) 3 · (1) 3 = 2 · - 4 8 = - 1 < 0

Значит, использовав 2 достаточное условие экстремума, получаем, что х = 1 является точкой максимума. Иначе запись имеет вид y m a x = y (1) = 8 1 1 + 1 = 4 .

Графическое изображение

Ответ: y m a x = y (1) = 4 ..

Функция y = f (x) имеет ее производную до n -го порядка в ε окрестности заданной точки x 0 и производную до n + 1 -го порядка в точке x 0 . Тогда f " (x 0) = f "" (x 0) = f " " " (x 0) = . . . = f n (x 0) = 0 .

Отсюда следует, что когда n является четным числом, то x 0 считается точкой перегиба, когда n является нечетным числом, то x 0 точка экстремума, причем f (n + 1) (x 0) > 0 , тогда x 0 является точкой минимума, f (n + 1) (x 0) < 0 , тогда x 0 является точкой максимума.

Пример 4

Найти точки максимума и минимума функции y y = 1 16 (x + 1) 3 (x - 3) 4 .

Решение

Исходная функция – целая рациональная, отсюда следует, что область определения – все действительные числа. Необходимо продифференцировать функцию. Получим, что

y " = 1 16 x + 1 3 " (x - 3) 4 + (x + 1) 3 x - 3 4 " = = 1 16 (3 (x + 1) 2 (x - 3) 4 + (x + 1) 3 4 (x - 3) 3) = = 1 16 (x + 1) 2 (x - 3) 3 (3 x - 9 + 4 x + 4) = 1 16 (x + 1) 2 (x - 3) 3 (7 x - 5)

Данная производная обратится в ноль при x 1 = - 1 , x 2 = 5 7 , x 3 = 3 . То есть точки могут быть точками возможного экстремума. Необходимо применить третье достаточное условие экстремума. Нахождение второй производной позволяет в точности определить наличие максимума и минимума функции. Вычисление второй производной производится в точках ее возможного экстремума. Получаем, что

y "" = 1 16 x + 1 2 (x - 3) 3 (7 x - 5) " = 1 8 (x + 1) (x - 3) 2 (21 x 2 - 30 x - 3) y "" (- 1) = 0 y "" 5 7 = - 36864 2401 < 0 y "" (3) = 0

Значит, что x 2 = 5 7 является точкой максимума. Применив 3 достаточный признак, получаем, что при n = 1 и f (n + 1) 5 7 < 0 .

Необходимо определить характер точек x 1 = - 1 , x 3 = 3 . Для этого необходимо найти третью производную, вычислить значения в этих точках. Получаем, что

y " " " = 1 8 (x + 1) (x - 3) 2 (21 x 2 - 30 x - 3) " = = 1 8 (x - 3) (105 x 3 - 225 x 2 - 45 x + 93) y " " " (- 1) = 96 ≠ 0 y " " " (3) = 0

Значит, x 1 = - 1 является точкой перегиба функции, так как при n = 2 и f (n + 1) (- 1) ≠ 0 . Необходимо исследовать точку x 3 = 3 . Для этого находим 4 производную и производим вычисления в этой точке:

y (4) = 1 8 (x - 3) (105 x 3 - 225 x 2 - 45 x + 93) " = = 1 2 (105 x 3 - 405 x 2 + 315 x + 57) y (4) (3) = 96 > 0

Из выше решенного делаем вывод, что x 3 = 3 является точкой минимума функции.

Графическое изображение

Ответ: x 2 = 5 7 является точкой максимума, x 3 = 3 - точкой минимума заданной функции.

Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter