Uproszczenie równań trygonometrycznych. Identyczne przekształcenia wyrażeń trygonometrycznych
Lekcja wideo „Simplifying Trigonometric Expressions” ma na celu rozwijanie umiejętności uczniów w rozwiązywaniu problemów trygonometrycznych przy użyciu podstawowych tożsamości trygonometrycznych. W trakcie lekcji wideo rozważane są rodzaje tożsamości trygonometrycznych, przykłady rozwiązywania problemów z ich wykorzystaniem. Korzystając z pomocy wizualnej, nauczycielowi łatwiej jest osiągnąć cele lekcji. Żywa prezentacja materiału pomaga zapamiętać ważne punkty. Zastosowanie efektów animacji i dubbingu pozwala na całkowite zastąpienie lektora na etapie wyjaśniania materiału. W ten sposób, wykorzystując tę pomoc wizualną na lekcjach matematyki, nauczyciel może zwiększyć efektywność nauczania.
Na początku lekcji wideo ogłaszany jest jej temat. Następnie przywołuje się zbadane wcześniej tożsamości trygonometryczne. Ekran wyświetla równości sin 2 t + cos 2 t = 1, tg t = sin t / cos t, gdzie t ≠ π / 2 + πk dla kϵZ, ctg t = cos t / sin t, ważne dla t ≠ πk, gdzie kϵZ, tg t · ctg t = 1, dla t ≠ πk / 2, gdzie kϵZ nazywamy podstawowymi tożsamościami trygonometrycznymi. Należy zauważyć, że tożsamości te są często używane w rozwiązywaniu problemów, w których konieczne jest udowodnienie równości lub uproszczenie wyrażenia.
Dalej rozważane są przykłady zastosowania tych tożsamości w rozwiązywaniu problemów. Po pierwsze, proponuje się rozważenie rozwiązania problemów w celu uproszczenia wyrażeń. W przykładzie 1 konieczne jest uproszczenie wyrażenia cos 2 t- cos 4 t + sin 4 t. Aby rozwiązać ten przykład, najpierw umieść wspólny czynnik cos 2 t poza nawiasami. W wyniku takiego przekształcenia w nawiasach otrzymuje się wyrażenie 1- cos 2 t, którego wartość z podstawowej tożsamości trygonometrii jest równa sin 2 t. Po przekształceniu wyrażenia oczywiste jest, że jeszcze jeden wspólny czynnik sin 2 t można umieścić w nawiasach, po czym wyrażenie przyjmuje postać sin 2 t (sin 2 t + cos 2 t). Z tej samej tożsamości podstawowej wyprowadzamy wartość wyrażenia w nawiasie, równą 1. W wyniku uproszczenia otrzymujemy cos 2 t- cos 4 t + sin 4 t = sin 2 t.
Przykład 2 wymaga również uproszczenia wyrażenia koszt / (1- sint) + koszt / (1+ sint). Ponieważ koszt wyrażenia znajduje się w licznikach obu ułamków, można go umieścić w nawiasach jako czynnik wspólny. Następnie ułamki w nawiasach są redukowane do wspólnego mianownika przez pomnożenie (1-sint) (1+ sint). Po dodaniu takich terminów w liczniku pozostaje 2, aw mianowniku 1 - grzech 2 t. Po prawej stronie ekranu przypominana jest podstawowa tożsamość trygonometryczna sin 2 t + cos 2 t = 1. Używając go, znajdujemy mianownik ułamka cos 2 t. Po zmniejszeniu ułamka otrzymujemy uproszczoną formę wyrażenia koszt / (1- sint) + koszt / (1+ sint) = 2 / koszt.
Dalej rozważane są przykłady dowodów tożsamości, w których wykorzystuje się wiedzę zdobytą na temat podstawowych tożsamości trygonometrii. W przykładzie 3 konieczne jest udowodnienie identyczności (tg 2 t-sin 2 t) · ctg 2 t = sin 2 t. Po prawej stronie ekranu wyświetlane są trzy tożsamości, które będą potrzebne do dowodu - tg t · ctg t = 1, ctg t = cos t / sin t oraz tan t = sin t / koszt t z ograniczeniami. Aby udowodnić identyczność, najpierw rozszerza się nawiasy, po czym tworzy się iloczyn odzwierciedlający wyrażenie głównej tożsamości trygonometrycznej tg t · ctg t = 1. Następnie, zgodnie z tożsamością z definicji kotangensa, transformuje się ctg 2 t. W wyniku przekształceń otrzymuje się wyrażenie 1-cos 2t. Wykorzystując tożsamość podstawową, odnajdujemy znaczenie wyrażenia. Tym samym udowodniono, że (tan 2 t-sin 2 t) ctg 2 t = sin 2 t.

W przykładzie 4 musisz znaleźć wartość wyrażenia tg 2 t + ctg 2 t, jeśli tg t + ctg t = 6. Aby obliczyć wyrażenie, prawa i lewa strona równości (tg t + ctg t) 2 = 6 2 są najpierw do kwadratu. Skrócona formuła mnożenia jest podobna do prawej strony ekranu. Po rozwinięciu nawiasów po lewej stronie wyrażenia powstaje suma tg 2 t + 2 · tg t · ctg t + ctg 2 t, dla której przekształcenia można uzyskać jedną z tożsamości trygonometrycznych tg t · ctg t = 1 zastosować, którego forma przypominana jest po prawej stronie ekranu. Po przekształceniu otrzymujemy równość tg 2 t + ctg 2 t = 34. Lewa strona równości pokrywa się ze stanem problemu, więc odpowiedź to 34. Problem rozwiązany.
Lekcja wideo „Simplifying Trigonometric Expressions” jest zalecana do wykorzystania na tradycyjnej szkolnej lekcji matematyki. Materiał przyda się także nauczycielowi prowadzącemu kształcenie na odległość. W celu rozwijania umiejętności rozwiązywania problemów trygonometrycznych.
KOD TEKSTOWY:
„Uproszczenie wyrażeń trygonometrycznych”.
Równość
1) sin 2 t + cos 2 t = 1 (sinus kwadrat te plus cosinus kwadrat te równa się jeden)
2) tgt =, dla t ≠ + πk, kϵZ (styczna te jest równa stosunkowi sinusa te do cosinusa te, gdy te nie jest równe pi przez dwa plus pi ka, ka należy do zet)
3) ctgt =, dla t ≠ πk, kϵZ (cotangens te jest równy stosunkowi cosinusa te do sinusa te, gdy te nie jest równe pikowi, ka należy do zet).
4) tgt ∙ ctgt = 1 dla t ≠, kϵZ (iloczyn stycznej te i cotangensa te jest równy jeden, jeśli te nie jest równe pikowi, podzielone przez dwa, ka należy do z)
nazywane są podstawowymi tożsamościami trygonometrycznymi.
Są często używane do uproszczenia i udowodnienia wyrażeń trygonometrycznych.
Spójrzmy na przykłady użycia tych wzorów do uproszczenia wyrażeń trygonometrycznych.
PRZYKŁAD 1: Uprość wyrażenie: cos 2 t - cos 4 t + sin 4 t. (wyrażenie to cosinus te kwadratowy minus cosinus te czwartego stopnia plus sinus te czwartego stopnia).
Rozwiązanie. cos 2 t - cos 4 t + sin 4 t = cos 2 t ∙ (1 - cos 2 t) + sin 4 t = cos 2 t ∙ sin 2 t + sin 4 t = sin 2 t (cos 2 t + sin 2 t) = grzech 2 t 1 = grzech 2 t
(wyjmujemy wspólny czynnik cosinus kwadrat te, w nawiasach otrzymujemy różnicę między jednostką a kwadratem cosinusa te, która jest równa przez pierwszą identyczność kwadratowi sinusa te. Otrzymujemy sumę sinusa czwartego stopnia te iloczynu cosinus kwadrat te i sinus kwadrat te. w nawiasach w nawiasach otrzymujemy sumę kwadratów cosinusa i sinusa, która przy podstawowej identyczności trygonometrycznej jest równa 1. W rezultacie otrzymujemy uzyskać kwadrat sinusa te).
PRZYKŁAD 2: Uprość wyrażenie: +.
(wyrażenie ba to suma dwóch ułamków w liczniku pierwszego cosinusa te w mianowniku jeden minus sin te, w liczniku drugiego cosinusa te w mianowniku druga jednostka plus sinus te).
(Wyjmijmy wspólny czynnik cosinus te z nawiasów, aw nawiasach podajemy go do wspólnego mianownika, który jest iloczynem jednego minus sinus te i jednego plus sinus te.
W liczniku otrzymujemy: jeden plus sine te plus jeden minus sine te, podajemy podobne, licznik jest równy dwóm po przyniesieniu podobnych.
W mianowniku można zastosować wzór skróconego mnożenia (różnicy kwadratów) i uzyskać różnicę między jednostką a kwadratem sinusa te, która zgodnie z podstawową tożsamością trygonometryczną
jest równy kwadratowi cosinusa te. Po anulowaniu przez cosinus te otrzymujemy ostateczną odpowiedź: dwa podzielone przez cosinus te).
Rozważmy przykłady użycia tych wzorów do dowodzenia wyrażeń trygonometrycznych.
PRZYKŁAD 3. Udowodnij identyczność (tg 2 t - sin 2 t) ∙ ctg 2 t = sin 2 t (iloczyn różnicy między kwadratami stycznej te i sinus te i kwadratem cotangens te jest równy kwadrat sinusa te).
Dowód.
Przekształćmy lewą stronę równości:
(tg 2 t - grzech 2 t) ∙ ctg 2 t = tg 2 t ∙ ctg 2 t - grzech 2 t ∙ ctg 2 t = 1 - grzech 2 t ∙ ctg 2 t = 1 - grzech 2 t ∙ = 1 - cos 2 t = grzech 2 t
(Otwórzmy nawiasy, z otrzymanej wcześniej zależności wiadomo, że iloczyn kwadratów stycznej te i cotangensa te jest równy jeden. Przypomnijmy, że cotangens te jest równy stosunkowi cosinusa te do sinusa te, co oznacza, że kwadrat cotangensa jest stosunkiem kwadratu cosinusa te do kwadratu sinusa te.
Po skreśleniu kwadratu te przez sinus otrzymujemy różnicę między jednostką a cosinusem kwadratu te, która jest równa sinusowi kwadratu te). co było do okazania

PRZYKŁAD 4 Znajdź wartość wyrażenia tg 2 t + ctg 2 t, jeśli tgt + ctgt = 6.
(suma kwadratów tangensa te i cotangensa te, jeśli suma tangensa i cotangensa wynosi sześć).
Rozwiązanie. (tgt + ctgt) 2 = 6 2
tg 2 t + 2 ∙ tgt ∙ ctgt + ctg 2 t = 36
tg 2 t + 2 + ctg 2 t = 36
tg 2 t + ctg 2 t = 36-2
tg 2 t + ctg 2 t = 34
Podnieśmy obie strony pierwotnej równości do kwadratu:
(tgt + ctgt) 2 = 6 2 (kwadrat sumy stycznej te i cotangensa te wynosi sześć do kwadratu). Przypomnijmy wzór na skrócone mnożenie: kwadrat sumy dwóch wielkości jest równy kwadratowi pierwszej plus dwukrotność iloczynu pierwszej przez drugą plus kwadrat drugiej. (a + b) 2 = a 2 + 2ab + b 2 Otrzymujemy tg 2 t + 2 ∙ tgt ∙ ctgt + ctg 2 t = 36 (styczna kwadrat te plus podwójny iloczyn stycznej te i cotangens te plus cotangens do kwadratu te równa się trzydzieści -sześć) ...

Ponieważ iloczyn stycznej te i cotangens te jest równy jeden, to tg 2 t + 2 + ctg 2 t = 36 (suma kwadratów stycznej te i cotangens te i dwa wynosi trzydzieści sześć),
Woronkowa Olga Iwanowna
MBOU „Szkoła średnia
nr 18”
Engels, obwód saratowski.
Nauczyciel matematyki.
„Wyrażenia trygonometryczne i ich przekształcenia”
Wprowadzenie ……………………………………………………………………… .... 3
Rozdział 1 Klasyfikacja zadań do wykorzystania przekształceń wyrażeń trygonometrycznych ………………………… …………………… ... 5
1.1. Zadania obliczeniowe wartości wyrażeń trygonometrycznych ……… .5
1.2.Zadania upraszczania wyrażeń trygonometrycznych ... 7
1.3. Zadania do konwersji liczbowych wyrażeń trygonometrycznych ... ..7
1.4 Zadania mieszane ………………………………………………… ..... 9
Rozdział 2. Metodologiczne aspekty organizacji końcowego powtórzenia tematu „Przemiana wyrażeń trygonometrycznych” ………………………………… 11
2.1 Powtórzenie tematyczne w klasie 10 ……………………………………… ... 11
Test 1 …………………………………………………………………………… ..12
Test 2 …………………………………………………………………………… ..13
Test 3 …………………………………………………………………………… ..14
2.2 Końcowe powtórki w klasie 11 ………………………………………… ... 15
Test 1 …………………………………………………………………………… ..17
Test 2 …………………………………………………………………………… ..17
Test 3 …………………………………………………………………………… ..18
Wniosek ………………………………………………………………… ....... 19
Wykaz wykorzystanej literatury ……………………………………… .. …… .20
Wstęp.
W dzisiejszych warunkach najważniejsze pytanie brzmi: „Jak możemy pomóc wyeliminować niektóre luki w wiedzy uczniów i ostrzec ich przed możliwymi błędami na egzaminie?” Aby rozwiązać ten problem, należy dążyć do uzyskania od studentów nie tyle formalnego przyswojenia materiału programowego, ale jego dogłębnego i świadomego zrozumienia, rozwoju szybkości ustnych obliczeń i przekształceń, a także rozwoju umiejętności rozwiązywania prostych problemów "w pamięci." Trzeba przekonywać uczniów, że tylko jeśli istnieje aktywna pozycja, w nauce matematyki, uzależniona od nabywania praktycznych umiejętności, umiejętności i ich wykorzystania, można liczyć na prawdziwy sukces. Należy wykorzystać każdą możliwość przygotowania się do UŻYTKOWANIA, w tym przedmioty fakultatywne w klasach 10-11, regularnie analizować z uczniami trudne zadania, wybierając najbardziej racjonalny sposób rozwiązywania na lekcjach i zajęciach dodatkowych.Pozytywny wynik wobszary rozwiązywania typowych problemów można osiągnąć, jeśli nauczyciele matematyki zechcą, tworzącdobre wykształcenie podstawowe uczniów, poszukiwanie nowych sposobów rozwiązywania problemów, które się przed nami otwierały, aktywne eksperymentowanie, stosowanie nowoczesnych technologii pedagogicznych, metod, technik, które stwarzają dogodne warunki do skutecznej samorealizacji i samostanowienia uczniów w nowych warunkach społecznych .
Trygonometria jest integralną częścią szkolnego kursu matematyki. Dobra wiedza i solidne umiejętności w zakresie trygonometrii świadczą o wystarczającym poziomie kultury matematycznej, niezbędnym warunku pomyślnego studiowania matematyki, fizyki, szeregu technicznych dyscypliny.
Trafność pracy. Znaczna część absolwentów szkół wykazuje z roku na rok bardzo słabe przygotowanie w tym ważnym dziale matematyki, o czym świadczą wyniki z lat ubiegłych (odsetek ukończenia w 2011 - 48,41%, 2012 - 51,05%), gdyż analiza zdanie jednolitego egzaminu państwowego pokazało, że studenci popełniają wiele błędów przy wykonywaniu zadań z tej konkretnej sekcji lub w ogóle takich zadań nie podejmują. W jednym Na egzaminie państwowym pytania z trygonometrii występują w prawie trzech rodzajach zadań. Jest to rozwiązanie najprostszych równań trygonometrycznych w zadaniu B5, praca z wyrażeniami trygonometrycznymi w zadaniu B7 oraz badanie funkcji trygonometrycznych w zadaniu B14, a także zadanie B12, które mają wzory opisujące zjawiska fizyczne i zawierają funkcje trygonometryczne. A to tylko część zadań B! Ale są też ulubione równania trygonometryczne z doborem pierwiastków C1 i „niezbyt ulubione” zadania geometryczne C2 i C4.
cel pracy. Przeanalizuj materiał Jednolitego Egzaminu Państwowego zadań B7, poświęconych przekształceniom wyrażeń trygonometrycznych i klasyfikuj zadania według formy ich prezentacji w testach.
Praca składa się z dwóch rozdziałów, wstępu i zakończenia. Wstęp podkreśla trafność pracy. Rozdział pierwszy zawiera klasyfikację zadań do wykorzystania transformacji wyrażeń trygonometrycznych w zadaniach testowych egzaminu Unified State Exam (2012).
W drugim rozdziale rozważa się organizację powtórki tematu „Transformacja wyrażeń trygonometrycznych” w klasach 10, 11 i opracowywane są testy na ten temat.
Spis literatury obejmuje 17 źródeł.
Rozdział 1. Klasyfikacja zadań do wykorzystania przekształceń wyrażeń trygonometrycznych.
Zgodnie ze standardem kształcenia średniego (pełnego) oraz wymaganiami dotyczącymi poziomu wyszkolenia uczniów, w kodyfikatorze wymagań zawarte są zadania dotyczące znajomości podstaw trygonometrii.
Nauka podstaw trygonometrii będzie najskuteczniejsza, gdy:
zapewniona zostanie pozytywna motywacja uczniów do powtarzania wcześniej przestudiowanego materiału;
w procesie edukacyjnym zostanie wdrożone podejście skoncentrowane na uczniu;
zastosowany zostanie system zadań, który przyczyni się do poszerzenia, pogłębienia, usystematyzowania wiedzy uczniów;
zastosowane zostaną zaawansowane technologie pedagogiczne.
Po przeanalizowaniu literatury i zasobów internetowych dotyczących przygotowania do egzaminu, zaproponowaliśmy jedną z możliwych klasyfikacji zadań B7 (KIM USE 2012-trygonometria): zadania do obliczaniawartości wyrażeń trygonometrycznych; zadania dlakonwersja liczbowych wyrażeń trygonometrycznych; zadania konwersji alfabetycznych wyrażeń trygonometrycznych; mieszane zadania.
1.1. Zadania obliczeniowe wartości wyrażeń trygonometrycznych.
Jednym z najczęstszych rodzajów prostych problemów trygonometrycznych jest obliczanie wartości funkcji trygonometrycznych przez wartość jednego z nich:
a) Posługiwanie się podstawową tożsamością trygonometryczną i jej konsekwencje.
Przykład 1
... Znajdź, jeśli  oraz
oraz  .
.
Rozwiązanie.  ,
,  ,
,
Ponieważ , następnie  .
.
Odpowiedź.
Przykład 2
... Odnaleźć  , Jeśli
, Jeśli  oraz .
oraz .
Rozwiązanie.  ,
,  ,
,  .
.
Ponieważ , następnie  .
.
Odpowiedź. ...
b) Stosowanie formuł z podwójnym kątem.
Przykład 3
... Odnaleźć  , Jeśli
, Jeśli  .
.
Rozwiązanie. ,  .
.
Odpowiedź.  .
.
Przykład 4
... Znajdź znaczenie wyrażenia  .
.
Rozwiązanie. ...
Odpowiedź.  .
.
1. Odnaleźć , Jeśli
 oraz
oraz  ... Odpowiedź. -0,2
... Odpowiedź. -0,2 2.
Odnaleźć , Jeśli  oraz
oraz  ... Odpowiedź. 0,4
... Odpowiedź. 0,4
 , Jeśli . Odpowiedź. -12,884.
Odnaleźć
, Jeśli . Odpowiedź. -12,884.
Odnaleźć  , Jeśli
, Jeśli  ... Odpowiedź. -0,845.
Znajdź znaczenie wyrażenia:
... Odpowiedź. -0,845.
Znajdź znaczenie wyrażenia: ... Odpowiedź. 66.
Znajdź znaczenie wyrażenia
... Odpowiedź. 66.
Znajdź znaczenie wyrażenia .Odpowiedź. -19
.Odpowiedź. -191.2.Zadania upraszczające wyrażenia trygonometryczne. Formuły odlewnicze powinny być dobrze opanowane przez studentów, ponieważ znajdą dalsze zastosowanie na lekcjach geometrii, fizyki i innych pokrewnych dyscyplin.
Przykład 5
.
Uprość wyrażenia  .
.
Rozwiązanie. ...
Odpowiedź.  .
.
Zadania samopomocy:
1. Uprość wyrażenie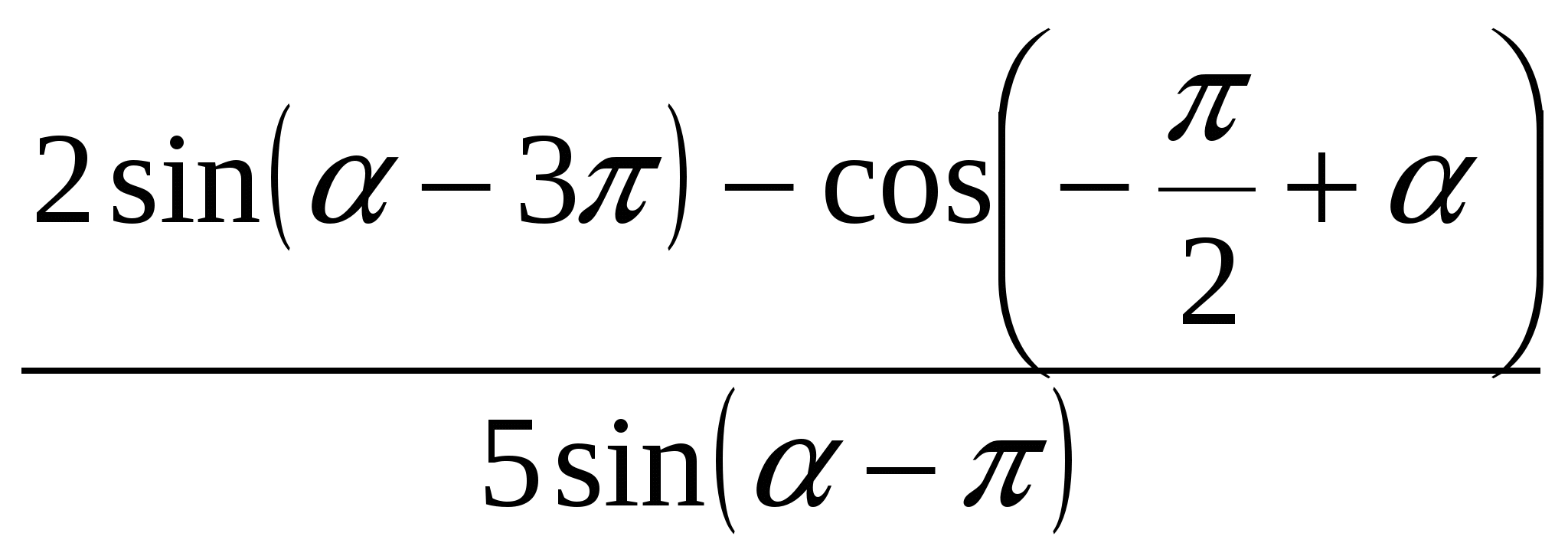 .
Odpowiedź. 0,62.
Odnaleźć
.
Odpowiedź. 0,62.
Odnaleźć  , Jeśli
, Jeśli  oraz... Odpowiedź. 10,563.
Znajdź znaczenie wyrażenia
oraz... Odpowiedź. 10,563.
Znajdź znaczenie wyrażenia  , Jeśli
, Jeśli  .
Odpowiedź. 2
.
Odpowiedź. 2 1.3. Zadania konwersji liczbowych wyrażeń trygonometrycznych.
Ćwicząc umiejętności i zdolności zadań do transformacji liczbowych wyrażeń trygonometrycznych, należy zwrócić uwagę na znajomość tabeli wartości funkcji trygonometrycznych, właściwości parzystości i okresowości funkcji trygonometrycznych.
a) Wykorzystanie dokładnych wartości funkcji trygonometrycznych dla niektórych kątów.
Przykład 6
... Oblicz  .
.
Rozwiązanie.  .
.
Odpowiedź.  .
.
b) Korzystanie z właściwości parzystości funkcje trygonometryczne.
Przykład 7
... Oblicz  .
.
Rozwiązanie. .
Odpowiedź. 
v) Korzystanie z właściwości okresowościfunkcje trygonometryczne.
Przykład 8
.
Znajdź znaczenie wyrażenia  .
.
Rozwiązanie. ...
Odpowiedź.  .
.
Zadania samopomocy:
1. Znajdź znaczenie wyrażenia .
Odpowiedź. -40,52. Znajdź znaczenie wyrażenia
.
Odpowiedź. -40,52. Znajdź znaczenie wyrażenia  .
Odpowiedź. 17
.
Odpowiedź. 17 3.
Znajdź znaczenie wyrażenia  .
Odpowiedź. 6
.
Odpowiedź. 6
 .
Odpowiedź. -24
.
Odpowiedź. -24  Odpowiedź. -64
Odpowiedź. -641.4 Zadania mieszane.
Testowa forma certyfikacji ma bardzo istotne cechy, dlatego ważne jest zwrócenie uwagi na zadania związane ze stosowaniem kilku formuł trygonometrycznych jednocześnie.
Przykład 9.
Odnaleźć  , Jeśli
, Jeśli  .
.
Rozwiązanie.  .
.
Odpowiedź.  .
.
Przykład 10
... Odnaleźć  , Jeśli
, Jeśli  oraz
oraz  .
.
Rozwiązanie. .
Ponieważ , następnie  .
.
Odpowiedź.  .
.
Przykład 11.
Odnaleźć  , Jeśli .
, Jeśli .
Rozwiązanie. , ,  ,
,  ,
,  ,
,  ,
,  .
.
Odpowiedź.
Przykład 12.
Oblicz  .
.
Rozwiązanie. .
Odpowiedź.  .
.
Przykład 13.
Znajdź znaczenie wyrażenia  , Jeśli
, Jeśli  .
.
Rozwiązanie. .
Odpowiedź.  .
.
Zadania samopomocy:
1. Odnaleźć , Jeśli
, Jeśli  .
Odpowiedź. -1,75
.
Odpowiedź. -1,752. Odnaleźć
 , Jeśli
, Jeśli  .
Odpowiedź. 33. Znajdź
.
Odpowiedź. 33. Znajdź  , Jeśli .Odpowiedź. 0,254. Znajdź znaczenie wyrażenia
, Jeśli .Odpowiedź. 0,254. Znajdź znaczenie wyrażenia  , Jeśli
, Jeśli  .
Odpowiedź. 0,35. Znajdź znaczenie wyrażenia
.
Odpowiedź. 0,35. Znajdź znaczenie wyrażenia  , Jeśli
, Jeśli  .
Odpowiedź. 5
.
Odpowiedź. 5Rozdział 2. Metodologiczne aspekty organizacji końcowego powtórzenia tematu „Transformacja wyrażeń trygonometrycznych”.
Jedną z najważniejszych kwestii wpływających na dalszą poprawę wyników w nauce, osiągnięcie przez studentów głębokiej i trwałej wiedzy jest kwestia powtarzania zaliczonego wcześniej materiału. Praktyka pokazuje, że w klasie 10 lepiej jest zorganizować powtórkę tematyczną; w klasie 11 - końcowe powtórka.
2.1. Powtórzenie tematyczne w klasie 10.
W procesie pracy z materiałem matematycznym szczególnie ważne jest powtarzanie każdego ukończonego tematu lub całej sekcji kursu.
Przy powtarzaniu tematycznym wiedza uczniów na dany temat jest usystematyzowana na końcowym etapie jego przejścia lub po przerwie.
W przypadku powtórzeń tematycznych przydzielane są specjalne lekcje, na których materiał jednego tematu jest skoncentrowany i uogólniony.
Powtórka na lekcji odbywa się poprzez rozmowę z szerokim zaangażowaniem uczniów w tę rozmowę. Następnie uczniowie są proszeni o powtórzenie określonego tematu i ostrzegani, że zostaną przeprowadzone prace testowe.
Test na dany temat powinien zawierać wszystkie podstawowe pytania. Po zakończeniu pracy analizowane są charakterystyczne błędy i organizowane są powtórki w celu ich wyeliminowania.
Na lekcje powtórek tematycznych proponujemy opracowane papiery testowe na temat „Konwersja wyrażeń trygonometrycznych”.
Test nr 1
Numer testu 2
Numer testu 3
Tabela odpowiedzi
Test
2.2. Końcowe powtórka w klasie 11.
Ostateczne powtórzenie odbywa się na ostatnim etapie studiowania głównych zagadnień kursu matematyki i odbywa się w logicznym związku z badaniem materiału edukacyjnego dla tej sekcji lub kursu jako całości.
Ostateczne powtórzenie materiału szkoleniowego ma następujące cele:
1. Aktywacja materiału całego szkolenia w celu wyjaśnienia jego logicznej struktury i zbudowania systemu w obrębie powiązań przedmiotowych i międzyprzedmiotowych.
2. Pogłębianie iw miarę możliwości poszerzanie wiedzy studentów na temat głównych zagadnień kursu w procesie powtórek.
Biorąc pod uwagę obowiązkowy egzamin z matematyki dla wszystkich absolwentów, stopniowe wprowadzanie Jednolitego Egzaminu Państwowego wymusza na nauczycielach nowe podejście do przygotowania i prowadzenia lekcji, uwzględniające konieczność zapewnienia wszystkim uczniom opanowania materiału edukacyjnego na poziomie podstawowym, gdyż a także możliwość dla zmotywowanych studentów zainteresowanych uzyskaniem wysokich ocen za przyjęcie na studia, dynamiczne postępy w opanowaniu materiału na poziomie zaawansowanym i wysokim.
Na lekcjach ostatniego powtórzenia możesz rozważyć następujące zadania:
Przykład 1 . Oblicz wartość wyrażenia.Rozwiązanie. = = =
= =  =
= =
= =
= =0,5.
Odpowiedź. 0,5. Przykład 2.
Określ największą wartość całkowitą, jaką może przyjąć wyrażenie
=0,5.
Odpowiedź. 0,5. Przykład 2.
Określ największą wartość całkowitą, jaką może przyjąć wyrażenie  .
.
Rozwiązanie. Ponieważ  może przyjmować dowolną wartość należącą do segmentu [–1; 1], wtedy
może przyjmować dowolną wartość należącą do segmentu [–1; 1], wtedy  przyjmuje dowolną wartość segmentu [–0,4; 0,4], zatem. Wartość całkowita wyrażenia to jeden - liczba 4.
przyjmuje dowolną wartość segmentu [–0,4; 0,4], zatem. Wartość całkowita wyrażenia to jeden - liczba 4.
 .
.
Rozwiązanie: Użyjmy wzoru na faktoryzację sumy kostek:. Mamy
Mamy:  .
.
Odpowiedź 1
Przykład 4.
Oblicz  .
.
Rozwiązanie. ...
Odpowiedź: 0,28
Na lekcje z ostatniego powtórzenia oferujemy opracowane testy na temat „Transformacja wyrażeń trygonometrycznych”.
Wprowadź największą liczbę całkowitą nieprzekraczającą 1
Wniosek.
Po zapoznaniu się z odpowiednią literaturą metodologiczną na ten temat możemy stwierdzić, że umiejętność i umiejętności rozwiązywania zadań związanych z transformacjami trygonometrycznymi w szkolnym kursie matematyki są bardzo ważne.
W trakcie prowadzonych prac dokonano klasyfikacji zadań B7. Uwzględniono formuły trygonometryczne najczęściej używane w CMM z 2012 roku. Podano przykłady zadań z rozwiązaniami. Testy różniczkowe zostały opracowane w celu uporządkowania powtórek i usystematyzowania wiedzy w ramach przygotowania do egzaminu.
Wskazane jest kontynuowanie rozpoczętej pracy poprzez rozważenie rozwiązywanie najprostszych równań trygonometrycznych w ćwiczeniu B5, badanie funkcji trygonometrycznych w ćwiczeniu B14, ćwiczenie B12, które zawierają wzory opisujące zjawiska fizyczne i zawierające funkcje trygonometryczne.
Podsumowując, pragnę zauważyć, że o skuteczności zaliczenia USE w dużej mierze decyduje to, jak skutecznie zorganizowany jest proces przygotowawczy na wszystkich etapach edukacji, ze wszystkimi kategoriami uczniów. A jeśli uda nam się ukształtować u uczniów samodzielność, odpowiedzialność i gotowość do kontynuowania nauki przez całe ich dalsze życie, to nie tylko wypełnimy porządek państwa i społeczeństwa, ale także podniesiemy własną samoocenę.
Powtórzenie materiału dydaktycznego wymaga od nauczyciela twórczej pracy. Musi zapewnić wyraźny związek między rodzajami powtórek, wdrożyć głęboko przemyślany system powtórek. Opanowanie sztuki organizowania powtórek jest zadaniem nauczyciela. Siła wiedzy uczniów w dużej mierze zależy od jej rozwiązania.
Literatura.
Vygodsky Ya.Ya., Podręcznik matematyki elementarnej. -M.: Nauka, 1970.
Problemy o podwyższonej trudności w algebrze i zasady analizy: Podręcznik dla klas 10-11 gimnazjum / B.M. Iwlew, rano Abramov, Yu.P. Dudnicyn, S.I. Schwarzburda. - M .: Edukacja, 1990.
Zastosowanie podstawowych formuł trygonometrycznych do transformacji wyrażeń (10 klasa) // Festiwal idei pedagogicznych. 2012-2013.
A.G. Koryanov , Prokofiew A.A. Przygotowujemy do egzaminu dobrych uczniów i doskonałych uczniów. - M .: Uniwersytet Pedagogiczny „Pierwszy września”, 2012. - 103 s.
Kuzniecowa E.N. Uproszczenie wyrażeń trygonometrycznych. Rozwiązywanie równań trygonometrycznych różnymi metodami (przygotowanie do egzaminu). 11 Klasa. 2012-2013.
Kulanin ED 3000 Problemy konkurencji w matematyce. 4. im., ks. i dodaj. - M .: Rolf, 2000.
Mordkovich A.G. Metodyczne problemy studiowania trygonometrii w szkole średniej // Matematyka w szkole. 2002. nr 6.
Pichurin L.F. O trygonometrii i nie tylko: -M. Edukacja, 1985
Reszetnikow N.N. Trygonometria w szkole: -M. : Wyższa Szkoła Pedagogiczna „Pierwszego września”, 2006, lk 1.
Szabunin MI, Prokofiew A.A. Matematyka. Algebra. Początek analizy matematycznej Poziom profilu: podręcznik do klasy 10 - M.: BINOM. Laboratorium wiedzy, 2007.
Portal edukacyjny do przygotowania do egzaminu.
Przygotowanie do egzaminu z matematyki „Och, ta trygonometria! http://festival.1september.ru/articles/621971/
Projekt "Matematyka? Łatwy !!!" http://www.resolventa.ru/
Sekcje: Matematyka
Klasa: 11
Lekcja 1
Temat: Klasa 11 (przygotowanie do egzaminu)
Uproszczenie wyrażeń trygonometrycznych.
Rozwiązywanie najprostszych równań trygonometrycznych. (2 godziny)
Cele:
- Usystematyzować, uogólnić, poszerzyć wiedzę i umiejętności studentów związane ze stosowaniem wzorów trygonometrycznych i rozwiązywaniem najprostszych równań trygonometrycznych.
Sprzęt do lekcji:
Struktura lekcji:
- Moment organizacyjny
- Testowanie na laptopach. Omówienie wyników.
- Upraszczanie wyrażeń trygonometrycznych
- Rozwiązywanie najprostszych równań trygonometrycznych
- Niezależna praca.
- Podsumowanie lekcji. Wyjaśnienie przydziału domu.
1. Moment organizacyjny. (2 minuty.)
Nauczyciel wita słuchaczy, ogłasza temat lekcji, przypomina o wcześniej zleconym zadaniu powtórzenia wzorów trygonometrii, przygotowuje uczniów do testów.
2. Testowanie. (15min + 3min dyskusji)
Celem jest sprawdzenie znajomości wzorów trygonometrycznych i umiejętności ich stosowania. Każdy uczeń ma na swoim biurku laptopa z wersją testową.
Opcji może być tyle ile chcesz, podam przykład jednej z nich:
Wariant I.
Uprość wyrażenia:
a) podstawowe tożsamości trygonometryczne
1.sin 2 3y + cos 2 3y + 1;
b) formuły dodawania
3.sin5x - sin3x;
c) przeliczenie produktu na sumę
6.2sin8y przytulny;
d) formuły podwójnego kąta
7.2sin5x cos5x;
e) formuły półkąta
f) formuły potrójnego kąta
g) powszechna substytucja
h) obniżenie stopnia
16.cos 2 (3x / 7);
Uczniowie na laptopie widzą swoje odpowiedzi obok każdej formuły.
Praca jest natychmiast sprawdzana przez komputer. Wyniki są wyświetlane na dużym ekranie, aby wszyscy mogli je zobaczyć.
Również po zakończeniu pracy na laptopach uczniów wyświetlane są prawidłowe odpowiedzi. Każdy uczeń widzi, gdzie popełniono błąd i jakie formuły musi powtórzyć.
3. Uproszczenie wyrażeń trygonometrycznych. (25 min.)
Celem jest przegląd, przećwiczenie i utrwalenie stosowania podstawowych wzorów trygonometrycznych. Rozwiązywanie problemów B7 z egzaminu.
Na tym etapie wskazane jest podzielenie klasy na grupy uczniów silnych (praca samodzielnie z późniejszą weryfikacją) i słabych, którzy pracują z nauczycielem.
Zadanie dla silnych uczniów (przygotowane wcześniej w formie drukowanej). Główny nacisk kładziony jest na formuły redukcji i podwójnego kąta, zgodnie z USE 2011.
Uprość wyrażenia (dla silnych uczniów):

Równolegle nauczyciel pracuje ze słabymi uczniami, omawiając i rozwiązując zadania na ekranie pod dyktando uczniów.
Oblicz:
5) grzech (270º - α) + cos (270º + α)
6) 
Uproszczać:

Przyszła kolej na dyskusję wyników pracy silnej grupy.
Na ekranie pojawiają się odpowiedzi, a także, za pomocą kamery wideo, wyświetlane są prace 5 różnych uczniów (po jednym zadaniu dla każdego).
Słaba grupa widzi warunek i sposób rozwiązania. Dyskusja i analiza są w toku. Za pomocą środków technicznych dzieje się to szybko.
4. Rozwiązywanie najprostszych równań trygonometrycznych. (30 minut.)
Celem jest powtórzenie, usystematyzowanie i uogólnienie rozwiązania najprostszych równań trygonometrycznych, rejestrując ich pierwiastki. Rozwiązanie problemu B3.
Każde równanie trygonometryczne, bez względu na to, jak je rozwiążemy, prowadzi do najprostszego.
Przy wykonywaniu zadania należy zwrócić uwagę na zapis pierwiastków równań poszczególnych przypadków i postać ogólną oraz wybór pierwiastków w ostatnim równaniu.
Rozwiąż równania:

Zapisz najmniejszy pozytywny pierwiastek w odpowiedzi.
5. Samodzielna praca (10 min.)
Celem jest przetestowanie nabytych umiejętności, zidentyfikowanie problemów, błędów i sposobów ich eliminacji.
Do wyboru studenta oferowana jest praca na różnym poziomie.
Opcja dla „3”
1) Znajdź wartość wyrażenia ![]()
2) Uprość wyrażenie 1 - sin 2 3α - cos 2 3α
3) Rozwiąż równanie ![]()
Opcja dla „4”
1) Znajdź wartość wyrażenia
2) Rozwiąż równanie ![]() Zapisz najmniejszy pierwiastek dodatni w odpowiedzi.
Zapisz najmniejszy pierwiastek dodatni w odpowiedzi.
Opcja dla „5”
1) Znajdź tgα jeśli ![]()
2) Znajdź pierwiastek równania ![]() Zapisz najmniejszy pierwiastek dodatni w swojej odpowiedzi.
Zapisz najmniejszy pierwiastek dodatni w swojej odpowiedzi.
6. Podsumowanie lekcji (5 min.)
Nauczyciel podsumowuje fakt, że na lekcji wzory trygonometryczne zostały powtórzone i utrwalone, rozwiązanie najprostszych równań trygonometrycznych.
Zadanie domowe (przygotowane wcześniej w formie drukowanej) z wyrywkową kontrolą na następnej lekcji.
Rozwiąż równania:

9) ![]()
10) ![]() Wskaż najmniejszy pierwiastek dodatni w swojej odpowiedzi.
Wskaż najmniejszy pierwiastek dodatni w swojej odpowiedzi.
Sesja 2
Temat: Klasa 11 (przygotowanie do egzaminu)
Metody rozwiązywania równań trygonometrycznych. Wybór korzeni. (2 godziny)
Cele:
- Uogólniać i usystematyzować wiedzę dotyczącą rozwiązywania równań trygonometrycznych różnych typów.
- Promowanie rozwoju myślenia matematycznego uczniów, umiejętności obserwacji, porównywania, uogólniania, klasyfikowania.
- Zachęć uczniów do pokonywania trudności w procesie aktywności umysłowej, do samokontroli, introspekcji swoich działań.
Sprzęt do lekcji: KRMu, laptopy dla każdego ucznia.
Struktura lekcji:
- Moment organizacyjny
- Dyskusja d/h i samot. prace z ostatniej lekcji
- Powtórzenie metod rozwiązywania równań trygonometrycznych.
- Rozwiązywanie równań trygonometrycznych
- Dobór pierwiastków w równaniach trygonometrycznych.
- Niezależna praca.
- Podsumowanie lekcji. Zadanie domowe.
1. Moment organizacyjny (2 min.)
Nauczyciel wita słuchaczy, ogłasza temat lekcji i plan pracy.
2. a) Przegląd prac domowych (5 min.)
Celem jest sprawdzenie wykonania. Jedna praca za pomocą kamery wideo jest wyświetlana na ekranie, pozostałe są selektywnie zbierane do sprawdzenia przez nauczyciela.
b) Analiza samodzielnej pracy (3 min.)
Celem jest analiza błędów, wskazanie sposobów ich przezwyciężenia.
Na ekranie, odpowiedzi i rozwiązania, uczniowie wstępnie wydali swoje prace. Analiza postępuje szybko.
3. Powtórzenie metod rozwiązywania równań trygonometrycznych (5 min.)
Celem jest przypomnienie metod rozwiązywania równań trygonometrycznych.
Zapytaj uczniów, jakie znają metody rozwiązywania równań trygonometrycznych. Podkreśl, że istnieją tak zwane podstawowe (często stosowane) metody:
- zmienna wymiana,
- faktoryzacja,
- równania jednorodne,
oraz stosowane są metody:
- przez formuły przeliczania sumy na produkt i produktu na sumę,
- według wzorów na obniżenie stopnia,
- uniwersalne podstawienie trygonometryczne
- wprowadzenie kąta pomocniczego,
- mnożenie przez jakąś funkcję trygonometryczną.
Należy również pamiętać, że jedno równanie można rozwiązać na różne sposoby.
4. Rozwiązywanie równań trygonometrycznych (30 min.)
Celem jest uogólnienie i utrwalenie wiedzy i umiejętności na ten temat, przygotowanie do decyzji C1 z egzaminu.
Uważam za celowe rozwiązanie równań dla każdej metody wspólnie z uczniami.
Uczeń dyktuje decyzję, nauczyciel zapisuje ją na tablecie, cały proces jest wyświetlany na ekranie. Umożliwi to szybkie i sprawne przywołanie wcześniej omówionego materiału.
Rozwiąż równania:
1) zmiana zmiennej 6cos 2 x + 5sinx - 7 = 0
2) faktoring 3cos (x / 3) + 4cos 2 (x / 3) = 0
3) równania jednorodne sin 2 x + 3cos 2 x - 2sin2x = 0
4) zamiana sumy na iloczyn cos5x + cos7x = cos (π + 6x)
5) zamiana iloczynu na sumę 2sinx sin2x + cos3x = 0
6) obniżenie mocy sin2x - sin 2 2x + sin 2 3x = 0,5
7) uniwersalne podstawienie trygonometryczne sinx + 5cosx + 5 = 0.
Rozwiązując to równanie należy zauważyć, że zastosowanie tej metody prowadzi do zawężenia dziedziny definicji, ponieważ sinus i cosinus są zastąpione przez tg (x/2). Dlatego przed wypisaniem odpowiedzi należy sprawdzić, czy liczby ze zbioru π + 2πn, n Z są końmi tego równania.
8) wprowadzenie kąta pomocniczego √3sinx + cosx - √2 = 0
9) mnożenie przez pewną funkcję trygonometryczną cosx cos2x cos4x = 1/8.
5. Wybór pierwiastków równań trygonometrycznych (20 min.)
Ponieważ w warunkach ostrej rywalizacji przy wchodzeniu na uczelnie rozwiązanie jednej pierwszej części egzaminu nie wystarczy, większość studentów powinna zwrócić uwagę na zadania z drugiej części (C1, C2, C3).
Dlatego celem tego etapu lekcji jest przypomnienie wcześniej przestudiowanego materiału, przygotowanie do rozwiązania problemu C1 z Unified State Examination w 2011 roku.
Istnieją równania trygonometryczne, w których podczas pisania odpowiedzi należy wybrać pierwiastki. Wynika to z pewnych ograniczeń, na przykład: mianownik ułamka nie wynosi zero, wyrażenie pod parzystym pierwiastkiem jest nieujemne, wyrażenie pod znakiem logarytmu jest dodatnie itp.
Takie równania są uważane za równania o podwyższonej złożoności iw wersji egzaminu znajdują się w drugiej części, czyli C1.
Rozwiązać równanie:
Ułamek wynosi zero, jeśli wtedy ![]() za pomocą koła jednostkowego wybierzemy pierwiastki (patrz rysunek 1)
za pomocą koła jednostkowego wybierzemy pierwiastki (patrz rysunek 1)

Obrazek 1.
otrzymujemy x = π + 2πn, n Z
Odpowiedź: π + 2πn, n Z
Na ekranie wybór korzeni jest pokazany na okręgu na kolorowym obrazie.
Iloczyn jest równy zero, gdy przynajmniej jeden z czynników jest równy zeru, a łuk w tym przypadku nie traci znaczenia. Następnie

Używając okręgu jednostkowego, wybierz korzenie (patrz rysunek 2)

Sekcje: Matematyka
Klasa: 11
Lekcja 1
Temat: Klasa 11 (przygotowanie do egzaminu)
Uproszczenie wyrażeń trygonometrycznych.
Rozwiązywanie najprostszych równań trygonometrycznych. (2 godziny)
Cele:
- Usystematyzować, uogólnić, poszerzyć wiedzę i umiejętności studentów związane ze stosowaniem wzorów trygonometrycznych i rozwiązywaniem najprostszych równań trygonometrycznych.
Sprzęt do lekcji:
Struktura lekcji:
- Moment organizacyjny
- Testowanie na laptopach. Omówienie wyników.
- Upraszczanie wyrażeń trygonometrycznych
- Rozwiązywanie najprostszych równań trygonometrycznych
- Niezależna praca.
- Podsumowanie lekcji. Wyjaśnienie przydziału domu.
1. Moment organizacyjny. (2 minuty.)
Nauczyciel wita słuchaczy, ogłasza temat lekcji, przypomina o wcześniej zleconym zadaniu powtórzenia wzorów trygonometrii, przygotowuje uczniów do testów.
2. Testowanie. (15min + 3min dyskusji)
Celem jest sprawdzenie znajomości wzorów trygonometrycznych i umiejętności ich stosowania. Każdy uczeń ma na swoim biurku laptopa z wersją testową.
Opcji może być tyle ile chcesz, podam przykład jednej z nich:
Wariant I.
Uprość wyrażenia:
a) podstawowe tożsamości trygonometryczne
1.sin 2 3y + cos 2 3y + 1;
b) formuły dodawania
3.sin5x - sin3x;
c) przeliczenie produktu na sumę
6.2sin8y przytulny;
d) formuły podwójnego kąta
7.2sin5x cos5x;
e) formuły półkąta
f) formuły potrójnego kąta
g) powszechna substytucja
h) obniżenie stopnia
16.cos 2 (3x / 7);
Uczniowie na laptopie widzą swoje odpowiedzi obok każdej formuły.
Praca jest natychmiast sprawdzana przez komputer. Wyniki są wyświetlane na dużym ekranie, aby wszyscy mogli je zobaczyć.
Również po zakończeniu pracy na laptopach uczniów wyświetlane są prawidłowe odpowiedzi. Każdy uczeń widzi, gdzie popełniono błąd i jakie formuły musi powtórzyć.
3. Uproszczenie wyrażeń trygonometrycznych. (25 min.)
Celem jest przegląd, przećwiczenie i utrwalenie stosowania podstawowych wzorów trygonometrycznych. Rozwiązywanie problemów B7 z egzaminu.
Na tym etapie wskazane jest podzielenie klasy na grupy uczniów silnych (praca samodzielnie z późniejszą weryfikacją) i słabych, którzy pracują z nauczycielem.
Zadanie dla silnych uczniów (przygotowane wcześniej w formie drukowanej). Główny nacisk kładziony jest na formuły redukcji i podwójnego kąta, zgodnie z USE 2011.
Uprość wyrażenia (dla silnych uczniów):

Równolegle nauczyciel pracuje ze słabymi uczniami, omawiając i rozwiązując zadania na ekranie pod dyktando uczniów.
Oblicz:
5) grzech (270º - α) + cos (270º + α)
6) 
Uproszczać:

Przyszła kolej na dyskusję wyników pracy silnej grupy.
Na ekranie pojawiają się odpowiedzi, a także, za pomocą kamery wideo, wyświetlane są prace 5 różnych uczniów (po jednym zadaniu dla każdego).
Słaba grupa widzi warunek i sposób rozwiązania. Dyskusja i analiza są w toku. Za pomocą środków technicznych dzieje się to szybko.
4. Rozwiązywanie najprostszych równań trygonometrycznych. (30 minut.)
Celem jest powtórzenie, usystematyzowanie i uogólnienie rozwiązania najprostszych równań trygonometrycznych, rejestrując ich pierwiastki. Rozwiązanie problemu B3.
Każde równanie trygonometryczne, bez względu na to, jak je rozwiążemy, prowadzi do najprostszego.
Przy wykonywaniu zadania należy zwrócić uwagę na zapis pierwiastków równań poszczególnych przypadków i postać ogólną oraz wybór pierwiastków w ostatnim równaniu.
Rozwiąż równania:

Zapisz najmniejszy pozytywny pierwiastek w odpowiedzi.
5. Samodzielna praca (10 min.)
Celem jest przetestowanie nabytych umiejętności, zidentyfikowanie problemów, błędów i sposobów ich eliminacji.
Do wyboru studenta oferowana jest praca na różnym poziomie.
Opcja dla „3”
1) Znajdź wartość wyrażenia ![]()
2) Uprość wyrażenie 1 - sin 2 3α - cos 2 3α
3) Rozwiąż równanie ![]()
Opcja dla „4”
1) Znajdź wartość wyrażenia
2) Rozwiąż równanie ![]() Zapisz najmniejszy pierwiastek dodatni w odpowiedzi.
Zapisz najmniejszy pierwiastek dodatni w odpowiedzi.
Opcja dla „5”
1) Znajdź tgα jeśli ![]()
2) Znajdź pierwiastek równania ![]() Zapisz najmniejszy pierwiastek dodatni w swojej odpowiedzi.
Zapisz najmniejszy pierwiastek dodatni w swojej odpowiedzi.
6. Podsumowanie lekcji (5 min.)
Nauczyciel podsumowuje fakt, że na lekcji wzory trygonometryczne zostały powtórzone i utrwalone, rozwiązanie najprostszych równań trygonometrycznych.
Zadanie domowe (przygotowane wcześniej w formie drukowanej) z wyrywkową kontrolą na następnej lekcji.
Rozwiąż równania:

9) ![]()
10) ![]() Wskaż najmniejszy pierwiastek dodatni w swojej odpowiedzi.
Wskaż najmniejszy pierwiastek dodatni w swojej odpowiedzi.
Sesja 2
Temat: Klasa 11 (przygotowanie do egzaminu)
Metody rozwiązywania równań trygonometrycznych. Wybór korzeni. (2 godziny)
Cele:
- Uogólniać i usystematyzować wiedzę dotyczącą rozwiązywania równań trygonometrycznych różnych typów.
- Promowanie rozwoju myślenia matematycznego uczniów, umiejętności obserwacji, porównywania, uogólniania, klasyfikowania.
- Zachęć uczniów do pokonywania trudności w procesie aktywności umysłowej, do samokontroli, introspekcji swoich działań.
Sprzęt do lekcji: KRMu, laptopy dla każdego ucznia.
Struktura lekcji:
- Moment organizacyjny
- Dyskusja d/h i samot. prace z ostatniej lekcji
- Powtórzenie metod rozwiązywania równań trygonometrycznych.
- Rozwiązywanie równań trygonometrycznych
- Dobór pierwiastków w równaniach trygonometrycznych.
- Niezależna praca.
- Podsumowanie lekcji. Zadanie domowe.
1. Moment organizacyjny (2 min.)
Nauczyciel wita słuchaczy, ogłasza temat lekcji i plan pracy.
2. a) Przegląd prac domowych (5 min.)
Celem jest sprawdzenie wykonania. Jedna praca za pomocą kamery wideo jest wyświetlana na ekranie, pozostałe są selektywnie zbierane do sprawdzenia przez nauczyciela.
b) Analiza samodzielnej pracy (3 min.)
Celem jest analiza błędów, wskazanie sposobów ich przezwyciężenia.
Na ekranie, odpowiedzi i rozwiązania, uczniowie wstępnie wydali swoje prace. Analiza postępuje szybko.
3. Powtórzenie metod rozwiązywania równań trygonometrycznych (5 min.)
Celem jest przypomnienie metod rozwiązywania równań trygonometrycznych.
Zapytaj uczniów, jakie znają metody rozwiązywania równań trygonometrycznych. Podkreśl, że istnieją tak zwane podstawowe (często stosowane) metody:
- zmienna wymiana,
- faktoryzacja,
- równania jednorodne,
oraz stosowane są metody:
- przez formuły przeliczania sumy na produkt i produktu na sumę,
- według wzorów na obniżenie stopnia,
- uniwersalne podstawienie trygonometryczne
- wprowadzenie kąta pomocniczego,
- mnożenie przez jakąś funkcję trygonometryczną.
Należy również pamiętać, że jedno równanie można rozwiązać na różne sposoby.
4. Rozwiązywanie równań trygonometrycznych (30 min.)
Celem jest uogólnienie i utrwalenie wiedzy i umiejętności na ten temat, przygotowanie do decyzji C1 z egzaminu.
Uważam za celowe rozwiązanie równań dla każdej metody wspólnie z uczniami.
Uczeń dyktuje decyzję, nauczyciel zapisuje ją na tablecie, cały proces jest wyświetlany na ekranie. Umożliwi to szybkie i sprawne przywołanie wcześniej omówionego materiału.
Rozwiąż równania:
1) zmiana zmiennej 6cos 2 x + 5sinx - 7 = 0
2) faktoring 3cos (x / 3) + 4cos 2 (x / 3) = 0
3) równania jednorodne sin 2 x + 3cos 2 x - 2sin2x = 0
4) zamiana sumy na iloczyn cos5x + cos7x = cos (π + 6x)
5) zamiana iloczynu na sumę 2sinx sin2x + cos3x = 0
6) obniżenie mocy sin2x - sin 2 2x + sin 2 3x = 0,5
7) uniwersalne podstawienie trygonometryczne sinx + 5cosx + 5 = 0.
Rozwiązując to równanie należy zauważyć, że zastosowanie tej metody prowadzi do zawężenia dziedziny definicji, ponieważ sinus i cosinus są zastąpione przez tg (x/2). Dlatego przed wypisaniem odpowiedzi należy sprawdzić, czy liczby ze zbioru π + 2πn, n Z są końmi tego równania.
8) wprowadzenie kąta pomocniczego √3sinx + cosx - √2 = 0
9) mnożenie przez pewną funkcję trygonometryczną cosx cos2x cos4x = 1/8.
5. Wybór pierwiastków równań trygonometrycznych (20 min.)
Ponieważ w warunkach ostrej rywalizacji przy wchodzeniu na uczelnie rozwiązanie jednej pierwszej części egzaminu nie wystarczy, większość studentów powinna zwrócić uwagę na zadania z drugiej części (C1, C2, C3).
Dlatego celem tego etapu lekcji jest przypomnienie wcześniej przestudiowanego materiału, przygotowanie do rozwiązania problemu C1 z Unified State Examination w 2011 roku.
Istnieją równania trygonometryczne, w których podczas pisania odpowiedzi należy wybrać pierwiastki. Wynika to z pewnych ograniczeń, na przykład: mianownik ułamka nie wynosi zero, wyrażenie pod parzystym pierwiastkiem jest nieujemne, wyrażenie pod znakiem logarytmu jest dodatnie itp.
Takie równania są uważane za równania o podwyższonej złożoności iw wersji egzaminu znajdują się w drugiej części, czyli C1.
Rozwiązać równanie:
Ułamek wynosi zero, jeśli wtedy ![]() za pomocą koła jednostkowego wybierzemy pierwiastki (patrz rysunek 1)
za pomocą koła jednostkowego wybierzemy pierwiastki (patrz rysunek 1)

Obrazek 1.
otrzymujemy x = π + 2πn, n Z
Odpowiedź: π + 2πn, n Z
Na ekranie wybór korzeni jest pokazany na okręgu na kolorowym obrazie.
Iloczyn jest równy zero, gdy przynajmniej jeden z czynników jest równy zeru, a łuk w tym przypadku nie traci znaczenia. Następnie

Używając okręgu jednostkowego, wybierz korzenie (patrz rysunek 2)

Rysunek 2.
5) ![]()
Przejdźmy do systemu:
![]()
W pierwszym równaniu układu wykonujemy logarytm zmian 2 (sinx) = y, otrzymujemy wtedy równanie ![]() , wróć do systemu
, wróć do systemu
wybierz korzenie za pomocą koła jednostkowego (patrz rysunek 5),

Rysunek 5.

6. Samodzielna praca (15 min.)
Celem jest utrwalenie i sprawdzenie przyswojenia materiału, zidentyfikowanie błędów, nakreślenie sposobów ich korygowania.
Praca oferowana jest w trzech wersjach, przygotowanych wcześniej w formie drukowanej, do wyboru przez studentów.
Możesz rozwiązywać równania w dowolny sposób.
Opcja dla „3”
Rozwiąż równania:
1) 2sin 2 x + sinx - 1 = 0
2) sin2x = √3cosx
Opcja dla „4”
Rozwiąż równania:
1) cos2x = 11sinx - 5
2) (2sinx + √3) log 8 (cosx) = 0
Opcja dla „5”
Rozwiąż równania:
1) 2sinx - 3cosx = 2
2) ![]()
7. Podsumowanie lekcji, praca domowa (5 min.)
Nauczyciel podsumowuje lekcję, po raz kolejny zwraca uwagę na to, że równanie trygonometryczne można rozwiązać na kilka sposobów. Najlepszym sposobem na osiągnięcie szybkich rezultatów jest ten, którego najlepiej uczy się indywidualny uczeń.
Przygotowując się do egzaminu, trzeba systematycznie powtarzać wzory i metody rozwiązywania równań.
Praca domowa (przygotowana wcześniej w formie drukowanej) jest rozdawana i komentuje, jak rozwiązać niektóre równania.
Rozwiąż równania:
1) cosx + cos5x = cos3x + cos7x
2) 5sin (x / 6) - cos (x / 3) + 3 = 0
3) 4sin 2 x + sin2x = 3
4) grzech 2 x + grzech 2 2x - grzech 2 3x - grzech 2 4x = 0
5) cos3x cos6x = cos4x cos7x
6) 4sinx - 6cosx = 1
7) 3sin2x + 4 cos2x = 5
8) cosx cos2x cos4x cos8x = (1/8) cos15x
9) (2sin 2 x - sinx) log 3 (2cos 2 x + cosx) = 0
10) (2cos 2 x - √3cosx) log 7 (-tgx) = 0
11) ![]()
V identyczne przekształcenia wyrażenia trygonometryczne można zastosować następujące techniki algebraiczne: dodawanie i odejmowanie tych samych terminów; usunięcie wspólnego czynnika z nawiasów; mnożenie i dzielenie przez tę samą kwotę; stosowanie skróconych wzorów mnożenia; wybór pełnego kwadratu; faktoryzacja trójmianu kwadratowego; wprowadzenie nowych zmiennych w celu uproszczenia przekształceń.
Podczas konwertowania wyrażeń trygonometrycznych zawierających ułamki można użyć właściwości proporcji, redukcji ułamków lub konwersji ułamków do wspólnego mianownika. Ponadto możesz użyć wyboru części całkowitej ułamka, mnożąc licznik i mianownik ułamka przez tę samą ilość i, jeśli to możliwe, uwzględnić jednorodność licznika lub mianownika. W razie potrzeby ułamek można przedstawić jako sumę lub różnicę kilku prostszych ułamków.
Ponadto, stosując wszystkie niezbędne metody konwersji wyrażeń trygonometrycznych, należy stale uwzględniać zakres dopuszczalnych wartości przekonwertowanych wyrażeń.
Spójrzmy na kilka przykładów.
Przykład 1.
Oblicz А = (sin (2x - π) cos (3π - x) + sin (2x - 9π / 2) cos (x + π / 2)) 2 + (cos (x - π / 2) cos ( 2x - 7π / 2) +
+
grzech (3π / 2 - x) grzech (2x -5π / 2)) 2
Rozwiązanie.
Z formuł redukcyjnych wynika:
grzech (2x - π) = -sin 2x; cos (3π-x) = -cos x;
grzech (2x - 9π / 2) = -cos 2x; cos (x + π / 2) = -sin x;
cos (x - π / 2) = sin x; cos (2x - 7π / 2) = -sin 2x;
grzech (3π / 2 - x) = -cos x; grzech (2x - 5π / 2) = -cos 2x.
Stąd na podstawie wzorów na dodawanie argumentów i podstawowej tożsamości trygonometrycznej otrzymujemy
A = (sin 2x cos x + cos 2x sin x) 2 + (-sin x sin 2x + cos x cos 2x) 2 = grzech 2 (2x + x) + cos 2 (x + 2x) =
= grzech 2 3x + cos 2 3x = 1
Odpowiedź 1.
Przykład 2.
Przekształć wyrażenie М = cos α + cos (α + β) cos γ + cos β - sin (α + β) sin γ + cos γ na iloczyn.
Rozwiązanie.
Z wzorów na dodawanie argumentów i wzorów na przekształcenie sumy funkcji trygonometrycznych w produkt po odpowiednim grupowaniu mamy
М = (cos (α + β) cos γ - sin (α + β) sin γ) + cos α + (cos β + cos γ) =
2cos ((β + γ) / 2) cos ((β - γ) / 2) + (cos α + cos (α + β + γ)) =
2cos ((β + γ) / 2) cos ((β - γ) / 2) + 2cos (α + (β + γ) / 2) cos ((β + γ) / 2)) =
2cos ((β + γ) / 2) (cos ((β - γ) / 2) + cos (α + (β + γ) / 2)) =
2cos ((β + γ) / 2) 2cos ((β - γ) / 2 + α + (β + γ) / 2) / 2) cos ((β - γ) / 2) - (α + ( β + γ) / 2) / 2) =
4cos ((β + γ) / 2) cos ((α + β) / 2) cos ((α + γ) / 2).
Odpowiedź: М = 4cos ((α + β) / 2) cos ((α + γ) / 2) cos ((β + γ) / 2).
Przykład 3.
Pokaż, że wyrażenie A = cos 2 (x + π / 6) - cos (x + π / 6) cos (x - π / 6) + cos 2 (x - π / 6) ma jedno i to samo znaczenie. Znajdź tę wartość.
Rozwiązanie.
Oto dwa sposoby rozwiązania tego problemu. Stosując pierwszą metodę, wybierając cały kwadrat i stosując odpowiednie podstawowe wzory trygonometryczne, otrzymujemy
А = (cos (x + π / 6) - cos (x - π / 6)) 2 + cos (x - π / 6) cos (x - π / 6) =
4sin 2 x sin 2 π / 6 + 1/2 (cos 2x + cos π / 3) =
Grzech 2 x + 1/2 cos 2x + 1/4 = 1/2 (1 - cos 2x) + 1/2 cos 2x + 1/4 = 3/4.
Rozwiązując problem w drugi sposób, rozważ A jako funkcję x od R i oblicz jego pochodną. Po przemianach otrzymujemy
A´ = -2cos (x + π / 6) sin (x + π / 6) + (sin (x + π / 6) cos (x - π / 6) + cos (x + π / 6) sin (x + π / 6)) - 2cos (x - π / 6) sin (x - π / 6) =
Grzech 2 (x + π / 6) + grzech ((x + π / 6) + (x - π / 6) - grzech 2 (x - π / 6) =
Grzech 2x - (grzech (2x + π / 3) + grzech (2x - π / 3)) =
Sin 2x - 2sin 2x cos π / 3 = sin 2x - sin 2x ≡ 0.
Stąd na mocy kryterium stałości funkcji różniczkowalnej na przedziale wnioskujemy, że
A (x) ≡ (0) = cos 2 π / 6 - cos 2 π / 6 + cos 2 π / 6 = (√3 / 2) 2 = 3/4, x € R. 
Odpowiedź: A = 3/4 dla x € R.
Główne metody udowadniania tożsamości trygonometrycznych to:
a) redukcja lewej strony tożsamości w prawo poprzez odpowiednie przekształcenia;
b) redukcja prawej strony tożsamości do lewej;
v) redukcja prawej i lewej części tożsamości do tego samego rodzaju;
G) sprowadzenie do zera różnicy między lewą i prawą stroną udowadniania tożsamości.
Przykład 4.
Sprawdź, czy cos 3x = -4cos x cos (x + π / 3) cos (x + 2π / 3).
Rozwiązanie.
Przekształcając prawą stronę tej tożsamości zgodnie z odpowiednimi wzorami trygonometrycznymi, mamy
4cos x cos (x + π / 3) cos (x + 2π / 3) =
2cos x (cos ((x + π / 3) + (x + 2π / 3)) + cos ((x + π / 3) - (x + 2π / 3))) =
2cos x (cos (2x + π) + cos π / 3) =
2cos x cos 2x - cos x = (cos 3x + cos x) - cos x = cos 3x.
Prawa strona tożsamości została zredukowana do lewej.
Przykład 5.
Udowodnić, że sin 2 α + sin 2 β + sin 2 γ - 2cos α cos β cos γ = 2 jeśli α, β, γ są kątami wewnętrznymi pewnego trójkąta.
Rozwiązanie.
Biorąc pod uwagę, że α, β, γ są kątami wewnętrznymi pewnego trójkąta, otrzymujemy, że
α + β + γ = π, a zatem γ = π - α - β.
sin 2 α + sin 2 β + sin 2 γ - 2 cos α cos β cos γ =
Sin 2 α + sin 2 β + sin 2 (π - α - β) - 2cos α cos β cos (π - α - β) =
Sin 2 α + sin 2 β + sin 2 (α + β) + (cos (α + β) + cos (α - β) (cos (α + β) =
Sin 2 α + sin 2 β + (sin 2 (α + β) + cos 2 (α + β)) + cos (α - β) (cos (α + β) =
1/2 · (1 - cos 2α) + ½ · (1 - cos 2β) + 1 + 1/2 · (cos 2α + cos 2β) = 2.
Udowodniono pierwotną równość.
Przykład 6.
Aby udowodnić, że jeden z kątów α, β, γ trójkąta jest równy 60 °, konieczne i wystarczające jest, aby sin 3α + sin 3β + sin 3γ = 0.
Rozwiązanie.
Stan tego problemu zakłada dowód konieczności i wystarczalności.
Najpierw udowodnijmy potrzebować.
Można wykazać, że
sin 3α + sin 3β + sin 3γ = -4cos (3α / 2) cos (3β / 2) cos (3γ / 2).
Stąd biorąc pod uwagę, że cos (3/2 60 °) = cos 90 ° = 0, otrzymujemy, że jeśli jeden z kątów α, β lub γ jest równy 60 °, to
cos (3α / 2) cos (3β / 2) cos (3γ / 2) = 0, a zatem sin 3α + sin 3β + sin 3γ = 0.
Pozwól nam teraz udowodnić adekwatność określony warunek.
Jeśli sin 3α + sin 3β + sin 3γ = 0, to cos (3α / 2) cos (3β / 2) cos (3γ / 2) = 0, a zatem
albo cos (3α / 2) = 0, albo cos (3β / 2) = 0 lub cos (3γ / 2) = 0.
Stąd,
lub 3α / 2 = π / 2 + πk, tj. α = π / 3 + 2πk / 3, 
lub 3β / 2 = π / 2 + πk, tj. β = π / 3 + 2πk / 3,
lub 3γ / 2 = π / 2 + πk,
te. γ = π / 3 + 2πk / 3, gdzie k Z.
Ponieważ α, β, γ są kątami trójkąta, mamy
0 < α < π, 0 < β < π, 0 < γ < π.
Dlatego dla α = π / 3 + 2πk / 3 lub β = π / 3 + 2πk / 3 lub
γ = π / 3 + 2πk / 3 wszystkich kϵZ pasuje tylko k = 0.
Stąd wynika, że albo α = π / 3 = 60 ° lub β = π / 3 = 60 ° lub γ = π / 3 = 60 °.
Stwierdzenie jest udowodnione.
Masz pytania? Nie wiesz, jak uprościć wyrażenia trygonometryczne?
Aby uzyskać pomoc od korepetytora - zarejestruj się.
Pierwsza lekcja jest bezpłatna!
strony, z pełnym lub częściowym skopiowaniem materiału, wymagany jest link do źródła.



