Batasan matematika untuk boneka: penjelasan, teori, contoh solusi. Menyelesaikan Batasan dengan Mengungkap Angka Ketidakpastian hingga Pangkat Minus Tak Terbatas
PELAJARAN 20
20.1 PENGUNGKAPAN KETIDAKPASTIAN SPESIES
Contoh 1
Selesaikan batas 
Pertama, mari kita coba substitusikan -1 ke dalam pecahan: 
Dalam hal ini, diperoleh apa yang disebut ketidakpastian.
Peraturan umum: jika pembilang dan penyebutnya mengandung polinomial, dan ada ketidakpastian bentuknya, maka diungkapkan Anda perlu memfaktorkan pembilang dan penyebutnya.
Untuk melakukan ini, paling sering Anda perlu menyelesaikan persamaan kuadrat dan/atau menggunakan rumus perkalian yang disingkat.
Mari kita faktorkan pembilangnya. 
Contoh 2
Hitung batas 
Mari kita faktorkan pembilang dan penyebutnya.
Penyebut pembilang: 
,
Metode mengalikan pembilang dan penyebut dengan ekspresi konjugasi
Kami terus mempertimbangkan ketidakpastian bentuknya
Jenis limit selanjutnya mirip dengan tipe sebelumnya. Satu-satunya hal, selain polinomial, kita akan menambahkan akar.
Contoh 3
Temukan batasnya 
Kalikan pembilang dan penyebutnya dengan ekspresi konjugasinya.
20.2 PENGUNGKAPAN KETIDAKPASTIAN SPESIES
Sekarang kita akan membahas kelompok limit ketika , dan fungsinya adalah pecahan yang pembilang dan penyebutnya mengandung polinomial
Contoh 4
Hitung batas 
Menurut aturan kami, kami akan mencoba mensubstitusikan tak terhingga ke dalam fungsi tersebut. Apa yang kita dapatkan di puncak? Ketakterbatasan. Dan apa yang terjadi di bawah? Juga tak terhingga. Jadi, kita menghadapi apa yang disebut ketidakpastian spesies. Orang mungkin berpikir bahwa jawabannya sudah siap, tetapi secara umum hal ini tidak terjadi, dan beberapa teknik solusi perlu diterapkan, yang sekarang akan kita pertimbangkan.
Bagaimana cara mengatasi limit jenis ini?
Pertama kita lihat pembilangnya dan cari pangkat tertinggi: 
Pangkat terdepan pada pembilangnya adalah dua.
Sekarang kita melihat penyebutnya dan juga mencari pangkat tertinggi: 
Derajat tertinggi penyebutnya adalah dua.
Kemudian kita pilih pangkat tertinggi dari pembilang dan penyebutnya: dalam contoh ini, keduanya sama dan sama dengan dua.
Jadi, cara penyelesaiannya adalah sebagai berikut: untuk mengungkapkan ketidakpastianAnda perlu membagi pembilang dan penyebutnya dengandi tingkat senior.
Bagilah pembilang dan penyebutnya dengan 
Ini dia jawabannya, dan bukan ketidakterbatasan sama sekali.
Apa yang secara fundamental penting dalam perancangan suatu keputusan?
Pertama, kami menunjukkan ketidakpastian, jika ada.
Kedua, disarankan untuk menghentikan solusi untuk penjelasan perantara. Saya biasanya menggunakan tanda, tidak memiliki arti matematis apa pun, tetapi berarti solusinya diinterupsi untuk penjelasan perantara.
Ketiga, dalam batasnya disarankan untuk menandai apa yang terjadi di mana. Ketika pekerjaan dibuat dengan tangan, akan lebih mudah untuk melakukannya dengan cara ini: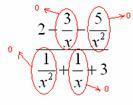 
Lebih baik menggunakan pensil sederhana untuk mencatat.
Tentu saja, Anda tidak perlu melakukan semua ini, tetapi mungkin guru akan menunjukkan kekurangan dalam solusi atau mulai mengajukan pertanyaan tambahan tentang tugas tersebut. Apakah Anda membutuhkannya?
Contoh 5
Temukan batasnya 
Sekali lagi pada pembilang dan penyebut kita temukan pada derajat tertinggi: 
Derajat maksimum pada pembilang: 3 Derajat maksimum pada penyebut: 4 Pilih terbesar nilai, dalam hal ini empat. Menurut algoritma kami, untuk mengungkapkan ketidakpastian, kami membagi pembilang dan penyebutnya dengan. Tugas lengkapnya mungkin terlihat seperti ini:
Contoh 6
Temukan batasnya 
Derajat maksimal “X” pada pembilangnya: 2 Derajat maksimal “X” pada penyebutnya: 1 (dapat dituliskan) Untuk mengetahui ketidakpastian, pembilang dan penyebutnya perlu dibagi. Solusi akhirnya mungkin terlihat seperti ini:
Bagilah pembilang dan penyebutnya dengan
Notasi bukan berarti pembagian dengan nol (tidak bisa dibagi dengan nol), melainkan pembagian dengan bilangan yang sangat kecil.
Jadi, dengan mengungkap ketidakpastian spesies, kita mungkin bisa melakukannya nomor akhir, nol atau tak terhingga.
PRAKTIKUM 20
TUGAS N 1
Larutan: Jika alih-alih variabel kita menempatkan nilai 7 yang cenderung, maka kita mendapatkan ketidakpastian bentuk 
TUGAS N 2Topik: Pengungkapan ketidakpastian tipe “zero to zero”.
Larutan: Jika alih-alih suatu variabel kita meletakkan nilai 0 yang cenderung, maka kita memperoleh ketidakpastian bentuk
TUGAS N 3Topik: Pengungkapan ketidakpastian tipe “zero to zero”.
Larutan: Jika alih-alih variabel kita menempatkan nilai 6 yang cenderung, maka kita mendapatkan ketidakpastian bentuk
TUGAS N 4
Larutan: Karena 
Dan 
TUGAS N 5Topik: Pengungkapan ketidakpastian bentuk “infinity to infinity”
Larutan: Karena 
Dan 
maka ada ketidakpastian bentuk.Untuk mengungkapnya, Anda perlu membagi setiap suku pembilang dan penyebutnya dengan. Kemudian, mengetahui apa yang kita dapatkan: 
KERJA MANDIRI 20
TUGAS N 1Topik: Pengungkapan ketidakpastian tipe “zero to zero”.
TUGAS N 2Topik: Pengungkapan ketidakpastian tipe “zero to zero”.
TUGAS N 3Topik: Pengungkapan ketidakpastian tipe “zero to zero”.
TUGAS N 4Topik: Pengungkapan ketidakpastian bentuk “infinity to infinity”
TUGAS N 5Topik: Pengungkapan ketidakpastian bentuk “infinity to infinity” Batas fungsi 
setara...
TUGAS N 6Topik: Pengungkapan ketidakpastian bentuk “infinity to infinity”
Turunan suatu fungsi tidak jauh letaknya, dan menurut aturan L'Hopital, turunan tersebut tepat berada di tempat fungsi aslinya berada. Keadaan ini membantu mengungkap ketidakpastian dalam bentuk 0/0 atau ∞/∞ dan beberapa ketidakpastian lain yang muncul saat menghitung membatasi hubungan dua fungsi yang sangat kecil atau sangat besar. Perhitungannya sangat disederhanakan dengan menggunakan aturan ini (sebenarnya ada dua aturan dan catatan untuknya):
Seperti yang terlihat dari rumus di atas, pada saat menghitung limit perbandingan dua fungsi yang sangat kecil atau sangat besar, maka limit perbandingan dua fungsi tersebut dapat diganti dengan limit perbandingan dua fungsi tersebut. turunan dan dengan demikian memperoleh hasil tertentu.
Mari kita beralih ke rumusan aturan L'Hopital yang lebih tepat.
Aturan L'Hopital untuk kasus limit dua besaran yang sangat kecil. Biarkan fungsinya F(X) Dan G(X A. Dan pada intinya A A turunan suatu fungsi G(X) bukan nol ( G"(X A sama satu sama lain dan sama dengan nol:
.
Aturan L'Hopital untuk kasus limit dua besaran tak terhingga. Biarkan fungsinya F(X) Dan G(X) memiliki turunan (yaitu, terdiferensiasi) di lingkungan titik tertentu A. Dan pada intinya A mereka mungkin tidak memiliki turunannya. Apalagi di sekitar titik tersebut A turunan suatu fungsi G(X) bukan nol ( G"(X)≠0) dan limit fungsi tersebut karena x cenderung terhadap nilai fungsi di titik tersebut A sama satu sama lain dan sama dengan tak terhingga:
.
Maka limit rasio fungsi-fungsi tersebut sama dengan limit rasio turunannya:
Dengan kata lain, untuk ketidakpastian berbentuk 0/0 atau ∞/∞, limit rasio dua fungsi sama dengan limit rasio turunannya, jika turunannya ada (berhingga, yaitu sama dengan a bilangan tertentu, atau tak terhingga, yaitu sama dengan tak terhingga).
Catatan.
1. Aturan L'Hopital juga berlaku pada saat fungsinya F(X) Dan G(X) tidak ditentukan kapan X = A.
2. Jika, saat menghitung limit perbandingan turunan fungsi F(X) Dan G(X) kita kembali menemui ketidakpastian berbentuk 0/0 atau ∞/∞, maka aturan L'Hôpital harus diterapkan berulang kali (minimal dua kali).
3. Aturan L'Hopital juga berlaku jika argumen fungsi (x) tidak cenderung ke bilangan berhingga A, dan hingga tak terhingga ( X → ∞).
Ketidakpastian tipe lain juga dapat direduksi menjadi ketidakpastian tipe 0/0 dan ∞/∞.
Pengungkapan ketidakpastian jenis “nol dibagi nol” dan “tak terhingga dibagi tak terhingga”
Contoh 1.
X=2 menyebabkan ketidakpastian dalam bentuk 0/0. Oleh karena itu, diperoleh turunan dari setiap fungsi
Turunan polinomial dihitung pada pembilangnya, dan pada penyebutnya - turunan dari fungsi logaritma kompleks. Sebelum tanda sama dengan terakhir, biasa saja membatasi, mengganti dua bukannya X.
Contoh 2. Hitung limit perbandingan dua fungsi menggunakan aturan L'Hopital:
Larutan. Mengganti nilai ke dalam fungsi tertentu X
Contoh 3. Hitung limit perbandingan dua fungsi menggunakan aturan L'Hopital:
Larutan. Mengganti nilai ke dalam fungsi tertentu X=0 menyebabkan ketidakpastian dalam bentuk 0/0. Oleh karena itu, kita menghitung turunan fungsi pembilang dan penyebutnya dan mendapatkan:
Contoh 4. Menghitung
Larutan. Mengganti nilai x yang sama dengan plus tak terhingga ke dalam suatu fungsi tertentu akan menimbulkan ketidakpastian dalam bentuk ∞/∞. Oleh karena itu, kami menerapkan aturan L'Hopital:
Komentar. Mari kita beralih ke contoh di mana aturan L'Hopital harus diterapkan dua kali, yaitu untuk sampai pada limit rasio turunan kedua, karena limit rasio turunan pertama adalah ketidakpastian berbentuk 0 /0 atau ∞/∞.
Mengungkap ketidakpastian dalam bentuk “nol kali tak terhingga”
Contoh 12. Menghitung
.
Larutan. Kita mendapatkan
Contoh ini menggunakan identitas trigonometri.
Pengungkapan ketidakpastian jenis "nol pangkat nol", "tak terhingga pangkat nol" dan "satu pangkat tak terhingga"
Ketidakpastian bentuk , atau biasanya direduksi menjadi bentuk 0/0 atau ∞/∞ dengan mengambil logaritma suatu fungsi dari bentuk tersebut
Untuk menghitung limit suatu ekspresi, Anda harus menggunakan identitas logaritma, kasus khusus yang merupakan properti logaritma 
.
Dengan menggunakan identitas logaritma dan sifat kontinuitas suatu fungsi (melampaui tanda limit), limitnya harus dihitung sebagai berikut:
Secara terpisah, Anda harus menemukan limit ekspresi dalam eksponen dan build e sampai tingkat yang ditemukan.
Contoh 13.
Larutan. Kita mendapatkan
.
.
Contoh 14. Hitung menggunakan aturan L'Hopital
Larutan. Kita mendapatkan
Hitung limit ekspresi dalam eksponen
.
.
Contoh 15. Hitung menggunakan aturan L'Hopital
Ketidakpastian ini “dilayani” batas indah kedua, dan di bagian kedua pelajaran itu kita melihat dengan sangat rinci contoh-contoh standar solusi yang ditemukan dalam praktik di banyak kasus. Sekarang gambar dengan eksponen akan selesai, selain itu, tugas akhir pelajaran akan dikhususkan untuk batas "salah", di mana TAMPAKNYA perlu menerapkan batas indah ke-2, meskipun ini sama sekali bukan batas yang tepat. kasus.
Kerugian dari kedua rumus kerja untuk limit luar biasa ke-2 ini adalah argumennya harus cenderung “plus tak terhingga” atau nol. Namun bagaimana jika argumentasinya cenderung ke arah yang berbeda?
Formula universal datang untuk menyelamatkan (yang sebenarnya merupakan konsekuensi dari batas luar biasa kedua):
Ketidakpastian dapat dihilangkan dengan menggunakan rumus:
Saya rasa saya sudah menjelaskan apa arti tanda kurung siku. Tidak ada yang istimewa, tanda kurung hanyalah tanda kurung. Mereka biasanya digunakan untuk menyorot notasi matematika dengan lebih jelas.
Mari kita soroti poin-poin penting dari rumus ini:
1) Ini tentang hanya tentang kepastian dan tidak ada yang lain.
2) Argumen “x” bisa cenderung nilai sewenang-wenang(dan bukan hanya ke nol atau), khususnya, ke “minus tak terhingga” atau ke siapa pun nomor terbatas.
Dengan menggunakan rumus ini Anda dapat menyelesaikan semua contoh dalam pelajaran. Batasan yang Luar Biasa, yang termasuk dalam batas luar biasa ke-2. Misalnya, mari kita hitung limitnya:
Pada kasus ini 
, dan menurut rumus 
:
Benar, saya tidak menyarankan melakukan hal ini; tradisinya adalah tetap menggunakan desain solusi yang “biasa”, jika bisa diterapkan. Namun menggunakan rumus sangat mudah untuk memeriksanya contoh "klasik" hingga batas luar biasa ke-2.
Semua ini baik dan benar, tetapi sekarang ada gambar yang lebih menarik dalam bingkai:
Contoh 18
Hitung batas 
Pada langkah pertama, saya tidak akan bosan mengulanginya, kita substitusikan nilai “x” ke dalam ekspresi di bawah tanda batas. Bagaimana jika tidak ada ketidakpastian sama sekali? Itu terjadi! Namun tidak saat ini. Mengganti “tiga”, kita sampai pada kesimpulan bahwa ada ketidakpastian di sini
Kami menggunakan rumusnya
Agar tidak menyeret huruf "e" ke mana-mana dan tidak membuatnya lebih kecil, indikatornya 
Lebih mudah untuk menghitung secara terpisah:
Pada kasus ini: 
Dengan demikian:
Dari sudut pandang teknologi perhitungan, semuanya rutin: pertama-tama kita mengurangi suku pertama menjadi penyebut yang sama, kemudian kita menghilangkan konstanta dan melakukan pengurangan, menghilangkan ketidakpastian 0:0.
Sebagai akibat: 
Hadiah yang dijanjikan dengan perbedaan logaritma dan ketidakpastian:
Contoh 19
Hitung batas
Pertama solusi lengkapnya, lalu komentar: 
(1)-(2) Dalam dua langkah pertama kita menggunakan rumus 
. kamu turunan kompleks kita “menghancurkan” logaritma, tetapi di sini, sebaliknya, logaritma tersebut perlu “dirakit”.
(3) Pindahkan ikon batas ke bawah logaritma. Hal ini dapat dilakukan karena logaritma ini kontinu ke "minus tak terhingga". Selain itu, limit mengacu pada “pengisian” logaritma.
(4)-(5) Teknik standar yang dibahas pada pelajaran dasar tentang batas yang luar biasa, kita ubah ketidakpastiannya menjadi bentuk .
(6) Kami menggunakan rumus .
(7) Fungsi eksponensial dan fungsi logaritma merupakan fungsi yang saling invers, oleh karena itu “e” dan logaritmanya dapat dihilangkan. Memang menurut sifat logaritma: . Kami menambahkan minus sebelum pecahan ke penyebutnya: 
(8) Tidak ada komentar =)
Jenis batasan yang dipertimbangkan tidak jarang, saya menemukan 30-40 contoh.
Contoh 20
Hitung batas 
Ini adalah contoh untuk Anda pecahkan sendiri. Selain menggunakan rumus, Anda dapat menyatakan limitnya sebagai 
dan dengan penggantian mengurangi solusi untuk kasus ini 
.
Kesimpulannya, mari kita lihat batasan “palsu”.
Mari kita kembali ke ketidakpastian. Ketidakpastian ini tidak selalu dapat direduksi menjadi ketidakpastian dan menggunakan rumus batas atau akibat wajar kedua yang luar biasa. Transformasi ini layak dilakukan jika pembilang dan penyebut alasnya - setara fungsi yang sangat besar. Misalnya: .
Mari kita istirahat dari indikator dan menghitung batas basisnya: 
Dalam batas yang didapat satuan, yang artinya pembilang dan penyebut tidak hanya dalam urutan pertumbuhan yang sama, tetapi juga setara. Di pelajaran Batasan yang luar biasa. Contoh solusi Kami dengan mudah mereduksi contoh ini menjadi ketidakpastian dan mendapatkan jawabannya.
Anda dapat menemukan banyak batasan serupa:
dll.
Pecahan dari contoh-contoh ini disatukan oleh fitur di atas: . Dalam kasus lain, jika ada ketidakpastian Batas luar biasa ke-2 tidak berlaku.
Contoh 21
Temukan batasannya
Betapapun kerasnya Anda berusaha, ketidakpastian tidak dapat diubah menjadi ketidakpastian
Berikut pembilang dan penyebut bilangan pokoknya tingkat pertumbuhan yang sama, namun tidak setara: 
.
Jadi, limit luar biasa kedua dan, khususnya rumusnya, TIDAK DAPAT DITERAPKAN.
! Catatan: Jangan bingung dengan Contoh #18, yang pembilang dan penyebut bilangan pokoknya tidak setara. Ada ketidakpastian yang sudah jadi, tapi di sini kita berbicara tentang ketidakpastian.
Cara menyelesaikan limit “palsu” sederhana dan bertanda: Anda memerlukan pembilang dan penyebut alasan bagi dengan “x” hingga pangkat tertinggi (berapapun eksponennya):
Jika pembilang dan penyebut alasnya berbeda ordonya, maka penyelesaiannya sama persis:
Contoh 22
Temukan batasannya 
Ini adalah contoh singkat untuk belajar mandiri
Kadang-kadang mungkin tidak ada ketidakpastian sama sekali:
Trik seperti itu sangat disukai oleh penyusun koleksi Kuznetsov. Itulah mengapa sangat penting untuk SELALU mengganti “x” ke dalam ekspresi di bawah tanda limit pada langkah pertama!
Contoh 2
Pembilang derajat mayor: 2; derajat penyebut tertinggi: 3.
:
Contoh 4
Bagilah pembilang dan penyebutnya dengan :
Catatan
: tindakan terakhir adalah mengalikan pembilang dan penyebutnya dengan untuk menghilangkan irasionalitas dalam penyebutnya.
Contoh 6
Bagilah pembilang dan penyebutnya dengan :
Contoh 8
Bagilah pembilang dan penyebutnya dengan :
Catatan
: ketentuan cenderung nol lebih lambat dari , Itu sebabnya adalah angka nol “utama” pada penyebutnya.
.
Contoh 22
Catatan
: fungsi yang sangat kecil cenderung nol lebih lambat dari , jadi angka nol penyebut yang “lebih besar” memainkan peran yang menentukan:
Batasan memberikan banyak masalah bagi semua siswa matematika. Untuk menyelesaikan suatu batasan, terkadang Anda harus menggunakan banyak trik dan memilih dari berbagai metode penyelesaian yang tepat untuk contoh tertentu.
Pada artikel ini kami tidak akan membantu Anda memahami batasan kemampuan Anda atau memahami batasan kendali, tetapi kami akan mencoba menjawab pertanyaan: bagaimana memahami batasan dalam matematika tingkat tinggi? Pemahaman datang dengan pengalaman, jadi pada saat yang sama kami akan memberikan beberapa contoh detail penyelesaian limit beserta penjelasannya.
Konsep limit dalam matematika
Pertanyaan pertama adalah: apa batasannya dan batasannya apa? Kita dapat berbicara tentang limit barisan dan fungsi numerik. Kami tertarik dengan konsep limit suatu fungsi, karena konsep inilah yang paling sering ditemui siswa. Tapi pertama-tama, definisi limit yang paling umum:
Katakanlah ada beberapa nilai variabel. Jika nilai ini dalam proses perubahan mendekati angka tertentu tanpa batas A , Itu A – batas nilai ini.
Untuk suatu fungsi yang didefinisikan dalam interval tertentu f(x)=kamu bilangan seperti itu disebut limit A , yang mana fungsinya cenderung kapan X , cenderung ke titik tertentu A . Dot A termasuk dalam interval di mana fungsi tersebut didefinisikan.
Kedengarannya rumit, tetapi penulisannya sangat sederhana:
Lim- dari bahasa Inggris membatasi- membatasi.
Ada juga penjelasan geometris untuk menentukan limit, namun di sini kita tidak akan mendalami teorinya, karena kita lebih tertarik pada sisi praktisnya daripada sisi teoritisnya. Saat kita mengatakan itu X cenderung suatu nilai, artinya variabel tersebut tidak mengambil nilai suatu bilangan, tetapi mendekatinya dengan jarak yang sangat dekat.
Mari kita beri contoh spesifik. Tugasnya adalah menemukan batasnya.
Untuk menyelesaikan contoh ini, kami mengganti nilainya x=3 menjadi suatu fungsi. Kita mendapatkan:
Omong-omong, jika Anda tertarik dengan operasi dasar matriks, baca artikel terpisah tentang topik ini.
Dalam contoh X dapat cenderung ke nilai apa pun. Itu bisa berupa angka berapa pun atau tak terhingga. Berikut ini contoh kapan X cenderung tak terhingga:
Secara intuitif, semakin besar angka penyebutnya, semakin kecil nilai fungsi tersebut. Jadi, dengan pertumbuhan tanpa batas X arti 1/x akan berkurang dan mendekati nol.
Seperti yang Anda lihat, untuk menyelesaikan limit, Anda hanya perlu mensubstitusikan nilai yang ingin diperjuangkan ke dalam fungsi X . Namun, ini adalah kasus yang paling sederhana. Seringkali menemukan batasannya tidak begitu jelas. Dalam batasan tersebut terdapat ketidakpastian jenisnya 0/0 atau tak terhingga/tak terhingga . Apa yang harus dilakukan dalam kasus seperti itu? Gunakan trik!
Ketidakpastian di dalam
Ketidakpastian bentuk tak terhingga/tak terhingga
Biarlah ada batasannya:
Jika kita mencoba mensubstitusikan tak terhingga ke dalam fungsi tersebut, kita akan mendapatkan tak terhingga pada pembilang dan penyebutnya. Secara umum, patut dikatakan bahwa ada elemen seni tertentu dalam menyelesaikan ketidakpastian tersebut: Anda perlu memperhatikan bagaimana Anda dapat mengubah fungsi sedemikian rupa sehingga ketidakpastian tersebut hilang. Dalam kasus kami, kami membagi pembilang dan penyebutnya dengan X di tingkat senior. Apa yang akan terjadi?
Dari contoh yang telah dibahas di atas, kita mengetahui bahwa suku-suku yang mengandung x pada penyebutnya akan cenderung nol. Maka penyelesaian limitnya adalah:
Untuk mengatasi ketidakpastian tipe tak terhingga/tak terhingga bagilah pembilang dan penyebutnya dengan X ke tingkat tertinggi.
Omong-omong! Untuk pembaca kami sekarang ada diskon 10%. jenis pekerjaan apa pun
Jenis ketidakpastian lainnya: 0/0
Seperti biasa, mengganti nilai ke dalam fungsi x=-1 memberi 0 pada pembilang dan penyebutnya. Perhatikan lebih dekat dan Anda akan melihat bahwa kita memiliki persamaan kuadrat pada pembilangnya. Mari kita cari akarnya dan tulis:
Mari kita kurangi dan dapatkan:
Jadi, jika Anda dihadapkan pada ketidakpastian tipe 0/0 – faktorkan pembilang dan penyebutnya.
Untuk memudahkan Anda menyelesaikan contoh, kami menyajikan tabel dengan limit beberapa fungsi:
Aturan L'Hopital di dalam
Cara ampuh lainnya untuk menghilangkan kedua jenis ketidakpastian tersebut. Apa inti dari metode ini?
Jika terdapat ketidakpastian pada limit, ambil turunan pembilang dan penyebutnya hingga ketidakpastian tersebut hilang.
Aturan L'Hopital terlihat seperti ini:
Poin penting : batas dimana harus ada turunan dari pembilang dan penyebutnya, bukan pembilang dan penyebutnya.
Dan sekarang - contoh nyata:
Ada ketidakpastian yang khas 0/0 . Mari kita ambil turunan dari pembilang dan penyebutnya:
Voila, ketidakpastian terselesaikan dengan cepat dan elegan.
Kami berharap Anda dapat menerapkan informasi ini dengan berguna dalam praktik dan menemukan jawaban atas pertanyaan “bagaimana menyelesaikan batasan dalam matematika tingkat tinggi.” Jika Anda perlu menghitung limit suatu barisan atau limit suatu fungsi pada suatu titik, dan sama sekali tidak ada waktu untuk pekerjaan ini, hubungi layanan pelajar profesional untuk mendapatkan solusi yang cepat dan terperinci.
Biasanya limit luar biasa kedua ditulis dalam bentuk ini:
\begin(persamaan) \lim_(x\to\infty)\left(1+\frac(1)(x)\right)^x=e\end(persamaan)
Angka $e$ yang ditunjukkan di sisi kanan persamaan (1) adalah irasional. Perkiraan nilai angka ini adalah: $e\approx(2(,)718281828459045)$. Jika kita melakukan penggantian $t=\frac(1)(x)$, maka rumus (1) dapat ditulis ulang sebagai berikut:
\begin(persamaan) \lim_(t\to(0))\biggl(1+t\biggr)^(\frac(1)(t))=e\end(persamaan)
Mengenai limit luar biasa pertama, tidak masalah ekspresi mana yang menggantikan variabel $x$ dalam rumus (1) atau sebagai ganti variabel $t$ dalam rumus (2). Hal utama adalah memenuhi dua syarat:
- Basis derajat (yaitu ekspresi dalam tanda kurung rumus (1) dan (2)) harus cenderung pada kesatuan;
- Eksponennya (yaitu $x$ dalam rumus (1) atau $\frac(1)(t)$ dalam rumus (2)) harus cenderung tak terhingga.
Batas luar biasa kedua dikatakan mengungkapkan ketidakpastian $1^\infty$. Harap dicatat bahwa dalam rumus (1) kita tidak menentukan tak terhingga ($+\infty$ atau $-\infty$) mana yang sedang kita bicarakan. Dalam semua kasus ini, rumus (1) benar. Dalam rumus (2), variabel $t$ bisa cenderung nol baik di kiri maupun di kanan.
Saya perhatikan bahwa ada juga beberapa konsekuensi berguna dari batas luar biasa kedua. Contoh penggunaan batas luar biasa kedua, serta konsekuensinya, sangat populer di kalangan penyusun perhitungan dan pengujian standar standar.
Contoh No.1
Hitung limit $\lim_(x\to\infty)\left(\frac(3x+1)(3x-5)\right)^(4x+7)$.
Mari kita segera perhatikan bahwa basis derajat (yaitu $\frac(3x+1)(3x-5)$) cenderung kesatuan:
$$ \lim_(x\to\infty)\frac(3x+1)(3x-5)=\kiri|\frac(\infty)(\infty)\kanan| =\lim_(x\ke\infty)\frac(3+\frac(1)(x))(3-\frac(5)(x)) =\frac(3+0)(3-0) = 1. $$
Dalam hal ini, eksponen (ekspresi $4x+7$) cenderung tak terhingga, yaitu. $\lim_(x\ke\infty)(4x+7)=\infty$.
Basis derajatnya cenderung satu, eksponennya cenderung tak terhingga, yaitu. kita berhadapan dengan ketidakpastian $1^\infty$. Mari kita terapkan rumus untuk mengungkap ketidakpastian ini. Dasar pangkat dari rumusnya adalah ekspresi $1+\frac(1)(x)$, dan dalam contoh yang kita pertimbangkan, dasar pangkatnya adalah: $\frac(3x+1)(3x- 5)$. Oleh karena itu, tindakan pertama adalah penyesuaian formal ekspresi $\frac(3x+1)(3x-5)$ ke bentuk $1+\frac(1)(x)$. Pertama, tambahkan dan kurangi satu:
$$ \lim_(x\ke\infty)\left(\frac(3x+1)(3x-5)\kanan)^(4x+7) =|1^\infty| =\lim_(x\ke\infty)\kiri(1+\frac(3x+1)(3x-5)-1\kanan)^(4x+7) $$
Harap dicatat bahwa Anda tidak bisa begitu saja menambahkan unit. Jika kita terpaksa menambahkan satu, maka kita juga perlu menguranginya agar tidak mengubah nilai keseluruhan ekspresi. Untuk melanjutkan solusinya, kami memperhitungkan hal itu
$$ \frac(3x+1)(3x-5)-1 =\frac(3x+1)(3x-5)-\frac(3x-5)(3x-5) =\frac(3x+1- 3x+5)(3x-5) =\frac(6)(3x-5). $$
Karena $\frac(3x+1)(3x-5)-1=\frac(6)(3x-5)$, maka:
$$ \lim_(x\to\infty)\left(1+ \frac(3x+1)(3x-5)-1\right)^(4x+7) =\lim_(x\to\infty)\ kiri(1+\frac(6)(3x-5)\kanan)^(4x+7) $$
Mari kita lanjutkan penyesuaiannya. Dalam rumus $1+\frac(1)(x)$, pembilang pecahan adalah 1, dan dalam persamaan $1+\frac(6)(3x-5)$ pembilangnya adalah $6$. Untuk mendapatkan $1$ pada pembilangnya, masukkan $6$ ke dalam penyebutnya menggunakan konversi berikut:
$$ 1+\frac(6)(3x-5) =1+\frac(1)(\frac(3x-5)(6)) $$
Dengan demikian,
$$ \lim_(x\to\infty)\left(1+\frac(6)(3x-5)\right)^(4x+7) =\lim_(x\to\infty)\left(1+ \frac(1)(\frac(3x-5)(6))\kanan)^(4x+7) $$
Jadi, dasar gelarnya, yaitu. $1+\frac(1)(\frac(3x-5)(6))$, disesuaikan dengan bentuk $1+\frac(1)(x)$ yang diperlukan dalam rumus. Sekarang mari kita mulai bekerja dengan eksponen. Perhatikan bahwa dalam rumus, ekspresi eksponen dan penyebutnya sama:
Artinya dalam contoh kita, eksponen dan penyebutnya harus disamakan. Untuk mendapatkan ekspresi $\frac(3x-5)(6)$ dalam eksponen, kita cukup mengalikan eksponen dengan pecahan ini. Tentu saja, untuk mengkompensasi perkalian seperti itu, Anda harus segera mengalikannya dengan pecahan kebalikannya, yaitu. oleh $\frac(6)(3x-5)$. Jadi kita punya:
$$ \lim_(x\to\infty)\left(1+\frac(1)(\frac(3x-5)(6))\right)^(4x+7) =\lim_(x\to\ infty)\left(1+\frac(1)(\frac(3x-5)(6))\right)^(\frac(3x-5)(6)\cdot\frac(6)(3x-5 )\cdot(4x+7)) =\lim_(x\to\infty)\left(\left(1+\frac(1)(\frac(3x-5)(6))\right)^(\ frac(3x-5)(6))\kanan)^(\frac(6\cdot(4x+7))(3x-5)) $$
Mari kita perhatikan secara terpisah limit pecahan $\frac(6\cdot(4x+7))(3x-5)$ yang terletak pada pangkat:
$$ \lim_(x\to\infty)\frac(6\cdot(4x+7))(3x-5) =\left|\frac(\infty)(\infty)\right| =\lim_(x\ke\infty)\frac(6\cdot\kiri(4+\frac(7)(x)\kanan))(3-\frac(5)(x)) =6\cdot\ frak(4)(3) =8. $$
Menjawab: $\lim_(x\to(0))\biggl(\cos(2x)\biggr)^(\frac(1)(\sin^2(3x)))=e^(-\frac(2) (9))$.
Contoh No.4
Tentukan limit $\lim_(x\to+\infty)x\left(\ln(x+1)-\ln(x)\right)$.
Karena untuk $x>0$ kita mempunyai $\ln(x+1)-\ln(x)=\ln\left(\frac(x+1)(x)\right)$, maka:
$$ \lim_(x\to+\infty)x\left(\ln(x+1)-\ln(x)\right) =\lim_(x\to+\infty)\left(x\cdot\ln\ kiri(\frac(x+1)(x)\kanan)\kanan) $$
Memperluas pecahan $\frac(x+1)(x)$ menjadi jumlah pecahan $\frac(x+1)(x)=1+\frac(1)(x)$ kita mendapatkan:
$$ \lim_(x\to+\infty)\left(x\cdot\ln\left(\frac(x+1)(x)\right)\right) =\lim_(x\to+\infty)\left (x\cdot\ln\left(1+\frac(1)(x)\right)\right) =\lim_(x\to+\infty)\left(\ln\left(\frac(x+1) (x)\kanan)^x\kanan) =\ln(e) =1. $$
Menjawab: $\lim_(x\to+\infty)x\kiri(\ln(x+1)-\ln(x)\kanan)=1$.
Contoh No.5
Tentukan limit $\lim_(x\to(2))\biggl(3x-5\biggr)^(\frac(2x)(x^2-4))$.
Karena $\lim_(x\to(2))(3x-5)=6-5=1$ dan $\lim_(x\to(2))\frac(2x)(x^2-4)= \ infty$, maka kita berhadapan dengan ketidakpastian dalam bentuk $1^\infty$. Penjelasan detailnya diberikan pada contoh no. 2, namun disini kami akan membatasi diri pada solusi singkatnya. Dengan melakukan penggantian $t=x-2$, kita mendapatkan:
$$ \lim_(x\to(2))\biggl(3x-5\biggr)^(\frac(2x)(x^2-4)) =\left|\begin(sejajar)&t=x-2 ;\;x=t+2\\&t\ke(0)\end(sejajar)\kanan| =\lim_(t\ke(0))\biggl(1+3t\biggr)^(\frac(2t+4)(t^2+4t))=\\ =\lim_(t\ke(0) )\biggl(1+3t\biggr)^(\frac(1)(3t)\cdot 3t\cdot\frac(2t+4)(t^2+4t)) =\lim_(t\ke(0) )\kiri(\biggl(1+3t\biggr)^(\frac(1)(3t))\kanan)^(\frac(6\cdot(t+2))(t+4)) =e^ 3. $$
Anda dapat menyelesaikan contoh ini dengan cara berbeda, menggunakan penggantian: $t=\frac(1)(x-2)$. Tentu saja jawabannya akan sama:
$$ \lim_(x\to(2))\biggl(3x-5\biggr)^(\frac(2x)(x^2-4)) =\left|\begin(sejajar)&t=\frac( 1)(x-2);\;x=\frac(2t+1)(t)\\&t\to\infty\end(sejajar)\kanan| =\lim_(t\ke\infty)\kiri(1+\frac(3)(t)\kanan)^(t\cdot\frac(4t+2)(4t+1))=\\ =\lim_ (t\ke\infty)\kiri(1+\frac(1)(\frac(t)(3))\kanan)^(\frac(t)(3)\cdot\frac(3)(t) \cdot\frac(t\cdot(4t+2))(4t+1)) =\lim_(t\ke\infty)\left(\left(1+\frac(1)(\frac(t)( 3))\kanan)^(\frac(t)(3))\kanan)^(\frac(6\cdot(2t+1))(4t+1)) =e^3. $$
Menjawab: $\lim_(x\to(2))\biggl(3x-5\biggr)^(\frac(2x)(x^2-4))=e^3$.
Contoh No.6
Tentukan limit $\lim_(x\to\infty)\left(\frac(2x^2+3)(2x^2-4)\right)^(3x) $.
Mari kita cari tahu kecenderungan ekspresi $\frac(2x^2+3)(2x^2-4)$ pada kondisi $x\to\infty$:
$$ \lim_(x\to\infty)\frac(2x^2+3)(2x^2-4) =\left|\frac(\infty)(\infty)\right| =\lim_(x\ke\infty)\frac(2+\frac(3)(x^2))(2-\frac(4)(x^2)) =\frac(2+0)(2 -0)=1. $$
Jadi, dalam batas tertentu kita menghadapi ketidakpastian dalam bentuk $1^\infty$, yang akan kita ungkapkan menggunakan batas luar biasa kedua:
$$ \lim_(x\to\infty)\left(\frac(2x^2+3)(2x^2-4)\kanan)^(3x) =|1^\infty| =\lim_(x\ke\infty)\kiri(1+\frac(2x^2+3)(2x^2-4)-1\kanan)^(3x)=\\ =\lim_(x\ke \infty)\left(1+\frac(7)(2x^2-4)\right)^(3x) =\lim_(x\to\infty)\left(1+\frac(1)(\frac (2x^2-4)(7))\kanan)^(3x)=\\ =\lim_(x\to\infty)\kiri(1+\frac(1)(\frac(2x^2-4 )(7))\kanan)^(\frac(2x^2-4)(7)\cdot\frac(7)(2x^2-4)\cdot 3x) =\lim_(x\to\infty) \kiri(\kiri(1+\frac(1)(\frac(2x^2-4)(7))\kanan)^(\frac(2x^2-4)(7))\kanan)^( \frac(21x)(2x^2-4)) =e^0 =1. $$
Menjawab: $\lim_(x\to\infty)\left(\frac(2x^2+3)(2x^2-4)\kanan)^(3x)=1$.
