त्रिकोणमितीय समीकरणों का सरलीकरण. त्रिकोणमितीय अभिव्यक्तियों की पहचान परिवर्तन
वीडियो पाठ "त्रिकोणमितीय अभिव्यक्तियों का सरलीकरण" बुनियादी त्रिकोणमितीय पहचानों का उपयोग करके त्रिकोणमितीय समस्याओं को हल करने में छात्रों के कौशल को विकसित करने के लिए डिज़ाइन किया गया है। वीडियो पाठ के दौरान, त्रिकोणमितीय पहचान के प्रकारों पर विचार किया जाता है, उनका उपयोग करके समस्याओं को हल करने के उदाहरण। दृश्य सामग्री के उपयोग से शिक्षक के लिए पाठ के उद्देश्यों को प्राप्त करना आसान हो जाता है। सामग्री की विशद प्रस्तुति महत्वपूर्ण बिंदुओं को याद रखने में योगदान करती है। एनीमेशन प्रभाव और आवाज अभिनय का उपयोग आपको सामग्री को समझाने के चरण में शिक्षक को पूरी तरह से बदलने की अनुमति देता है। इस प्रकार, गणित के पाठों में इस दृश्य सहायता का उपयोग करके शिक्षक शिक्षण की प्रभावशीलता को बढ़ा सकते हैं।
वीडियो पाठ की शुरुआत में इसके विषय की घोषणा की जाती है। फिर पहले अध्ययन की गई त्रिकोणमितीय पहचानों को याद किया जाता है। स्क्रीन समानताएं प्रदर्शित करती है पाप 2 t+cos 2 t=1, tg t=sin t/cos t, जहां kϵZ के लिए t≠π/2+πk, ctg t=cos t/sin t, t≠πk के लिए सत्य है, जहां kϵZ, tg t · ctg t=1, t≠πk/2 पर, जहां kϵZ, बुनियादी त्रिकोणमितीय पहचान कहलाती है। यह ध्यान दिया जाता है कि इन पहचानों का उपयोग अक्सर उन समस्याओं को हल करने में किया जाता है जहां समानता साबित करना या अभिव्यक्ति को सरल बनाना आवश्यक होता है।
इसके अलावा, समस्याओं को हल करने में इन पहचानों के अनुप्रयोग के उदाहरणों पर विचार किया गया है। सबसे पहले, अभिव्यक्तियों को सरल बनाने की समस्याओं को हल करने पर विचार करना प्रस्तावित है। उदाहरण 1 में, व्यंजक cos 2 t-cos 4 t+sin 4 t को सरल बनाना आवश्यक है। उदाहरण को हल करने के लिए, सामान्य गुणनखंड cos 2 t को पहले कोष्ठक में रखा गया है। कोष्ठकों में इस तरह के परिवर्तन के परिणामस्वरूप, अभिव्यक्ति 1-cos 2 t प्राप्त होती है, जिसका त्रिकोणमिति की मूल पहचान से मान पाप 2 t के बराबर होता है। अभिव्यक्ति के परिवर्तन के बाद, यह स्पष्ट है कि एक और सामान्य कारक पाप 2 टी को कोष्ठक से बाहर निकाला जा सकता है, जिसके बाद अभिव्यक्ति पाप 2 टी (sin 2 t + cos 2 t) का रूप लेती है। उसी मूल पहचान से, हम 1 के बराबर कोष्ठक में अभिव्यक्ति का मान निकालते हैं। सरलीकरण के परिणामस्वरूप, हम cos 2 t-cos 4 t+ पाप 4 t= पाप 2 t प्राप्त करते हैं।
उदाहरण 2 में, अभिव्यक्ति लागत/(1- सिंट)+ लागत/(1+ सिंट) को भी सरल बनाने की आवश्यकता है। चूंकि अभिव्यक्ति लागत दोनों भिन्नों के अंशों में है, इसलिए इसे एक सामान्य कारक के रूप में वर्गीकृत किया जा सकता है। फिर कोष्ठक में भिन्नों को (1-सिंट)(1+सिंट) से गुणा करके एक सामान्य हर में घटा दिया जाता है। समान पदों की कमी के बाद, अंश में 2 रहता है, और हर में 1 - पाप 2 टी रहता है। स्क्रीन के दाईं ओर, मूल त्रिकोणमितीय पहचान syn 2 t+cos 2 t=1 को याद किया जाता है। इसका उपयोग करके, हम भिन्न cos 2 t का हर ज्ञात करते हैं। अंश को कम करने के बाद, हमें अभिव्यक्ति लागत / (1-सिंट) + लागत / (1 + सिंत) \u003d 2 / लागत का सरलीकृत रूप मिलता है।
इसके बाद, हम सर्वसमिकाओं को सिद्ध करने के उदाहरणों पर विचार करते हैं जिनमें त्रिकोणमिति की मूल सर्वसमिकाओं के बारे में अर्जित ज्ञान को लागू किया जाता है। उदाहरण 3 में, पहचान सिद्ध करना आवश्यक है (tg 2 t-sin 2 t)·ctg 2 t=sin 2 t। स्क्रीन के दाईं ओर तीन पहचान प्रदर्शित होती हैं जिनकी प्रमाण के लिए आवश्यकता होगी - tg t ctg t=1, ctg t=cos t/sin t और tg t=sin t/cos t प्रतिबंधों के साथ। पहचान सिद्ध करने के लिए सबसे पहले कोष्ठक खोले जाते हैं, जिसके बाद एक उत्पाद बनता है जो मुख्य त्रिकोणमितीय पहचान tg t·ctg t=1 की अभिव्यक्ति को दर्शाता है। फिर, कोटैंजेंट की परिभाषा से पहचान के अनुसार, ctg 2 t रूपांतरित हो जाता है। परिवर्तनों के परिणामस्वरूप, अभिव्यक्ति 1-cos 2 t प्राप्त होती है। मूल पहचान का उपयोग करके, हम अभिव्यक्ति का मूल्य पाते हैं। इस प्रकार, यह सिद्ध हो गया है कि (tg 2 t-sin 2 t)·ctg 2 t=sin 2 t।

उदाहरण 4 में, आपको अभिव्यक्ति tg 2 t+ctg 2 t का मान ज्ञात करना होगा यदि tg t+ctg t=6। अभिव्यक्ति का मूल्यांकन करने के लिए, समीकरण (tg t+ctg t) 2 =6 2 के दाएं और बाएं पक्षों को पहले वर्गित किया जाता है। संक्षिप्त गुणन सूत्र स्क्रीन के दाईं ओर प्रदर्शित होता है। अभिव्यक्ति के बाईं ओर कोष्ठक खोलने के बाद, योग tg 2 t+2 tg t ctg t+ctg 2 t बनता है, जिसके परिवर्तन के लिए त्रिकोणमितीय पहचान tg t ctg t=1 में से एक को लागू किया जा सकता है, जिसका प्रपत्र स्क्रीन के दाईं ओर याद किया जाता है। परिवर्तन के बाद, समानता tg 2 t+ctg 2 t=34 प्राप्त होती है। समानता का बायां पक्ष समस्या की स्थिति से मेल खाता है, इसलिए उत्तर 34 है। समस्या हल हो गई है।
पारंपरिक स्कूली गणित पाठ में उपयोग के लिए वीडियो पाठ "त्रिकोणमितीय अभिव्यक्तियों को सरल बनाना" की अनुशंसा की जाती है। साथ ही, यह सामग्री दूरस्थ शिक्षा प्रदान करने वाले शिक्षक के लिए भी उपयोगी होगी। त्रिकोणमितीय समस्याओं को हल करने में कौशल विकसित करने के लिए।
पाठ व्याख्या:
"त्रिकोणमितीय अभिव्यक्तियों का सरलीकरण"।
समानता
1)sin 2 t + cos 2 t = 1 (sine का वर्ग te और कोज्या का वर्ग te एक के बराबर होता है)
2) tgt =, t ≠ + πk, kϵZ पर (te की स्पर्शरेखा, te की ज्या और te की कोज्या के अनुपात के बराबर होती है जब te, pi के बराबर नहीं है और pi का दो जोड़ है, ka zet से संबंधित है)
3) ctgt =, t ≠ πk, kϵZ पर (te का कोटैंजेंट, te की कोज्या और te की ज्या के अनुपात के बराबर होता है जब te, ka के शिखर के बराबर नहीं होता है, जो z से संबंधित है)।
4)tgt ∙ ctgt = 1 for t ≠ , kϵZ
बुनियादी त्रिकोणमितीय सर्वसमिकाएँ कहलाती हैं।
प्रायः इनका उपयोग त्रिकोणमितीय व्यंजकों को सरल बनाने तथा सिद्ध करने में किया जाता है।
त्रिकोणमितीय व्यंजकों को सरल बनाते समय इन सूत्रों के उपयोग के उदाहरणों पर विचार करें।
उदाहरण 1. अभिव्यक्ति को सरल बनाएं: cos 2 t - cos 4 t + syn 4 t। (अभिव्यक्ति a कोज्या वर्ग te शून्य से te की चौथी डिग्री की कोज्या प्लस te की चौथी डिग्री की sine)।
समाधान। कॉस 2 टी - कॉस 4 टी + पाप 4 टी = कॉस 2 टी∙ (1 - कॉस 2 टी) + पाप 4 टी = कॉस 2 टी ∙ पाप 2 टी + पाप 4 टी = पाप 2 टी (कॉस 2 टी + पाप 2 टी) = पाप 2 टी 1= पाप 2 टी
(हम उभयनिष्ठ गुणनखंड कोज्या वर्ग ते को निकालते हैं, कोष्ठक में हमें एकता और कोज्या ते के वर्ग के बीच का अंतर मिलता है, जो पहली पहचान से ज्या ते के वर्ग के बराबर होता है। हमें चौथे की ज्या का योग मिलता है कोसाइन वर्ग टी और साइन वर्ग टी के गुणनफल की डिग्री टी। हम कोष्ठक के बाहर सामान्य गुणनखंड साइन वर्ग टी निकालते हैं, कोष्ठक में हमें कोसाइन और साइन के वर्गों का योग मिलता है, जो मूल त्रिकोणमिति के अनुसार होता है पहचान, 1 के बराबर है। परिणामस्वरूप, हमें साइन टी का वर्ग मिलता है)।
उदाहरण 2. व्यंजक को सरल कीजिए: + .
(अभिव्यक्ति be पहली कोज्या te के अंश में दो भिन्नों का योग है, हर में एक घटा sine te है, दूसरी कोज्या te के अंश में दूसरे के हर में एक जमा sine te है)।
(हम सामान्य कारक कोसाइन टी को कोष्ठक से बाहर निकालते हैं, और कोष्ठक में हम इसे एक सामान्य हर में लाते हैं, जो एक माइनस साइन टी बटा एक प्लस साइन टी का गुणनफल है।
अंश में हमें मिलता है: एक प्लस साइन टी प्लस एक माइनस साइन टी, हम समान देते हैं, समान लाने के बाद अंश दो के बराबर होता है।
हर में, आप संक्षिप्त गुणन सूत्र (वर्गों का अंतर) लागू कर सकते हैं और साइन टी की इकाई और वर्ग के बीच का अंतर प्राप्त कर सकते हैं, जो मूल त्रिकोणमितीय पहचान के अनुसार है
कोसाइन टी के वर्ग के बराबर है। कोज्या ते से घटाने के बाद, हमें अंतिम उत्तर मिलता है: दो को कोज्या ते से विभाजित किया जाता है)।
त्रिकोणमितीय व्यंजकों को सिद्ध करने में इन सूत्रों के उपयोग के उदाहरणों पर विचार करें।
उदाहरण 3. पहचान साबित करें (टीजी 2 टी - पाप 2 टी) ∙ सीटीजी 2 टी \u003d पाप 2 टी (टी की स्पर्शरेखा के वर्गों और टी की साइन और कोटैंजेंट के वर्ग के बीच अंतर का उत्पाद) te, te की ज्या के वर्ग के बराबर है)।
सबूत।
आइए समानता के बाएँ पक्ष को रूपांतरित करें:
(टीजी 2 टी - पाप 2 टी) ∙ सीटीजी 2 टी = टीजी 2 टी ∙ सीटीजी 2 टी - पाप 2 टी ∙ सीटीजी 2 टी = 1 - पाप 2 टी ∙ सीटीजी 2 टी =1 - पाप 2 टी ∙ = 1 - कॉस 2 टी = पाप 2 टी
(आइए कोष्ठक खोलें, पहले प्राप्त संबंध से यह ज्ञात है कि te की स्पर्शरेखा के वर्गों का te के कोटैंजेंट द्वारा गुणनफल एक के बराबर है। याद रखें कि te का कोटैंजेंट, की कोज्या के अनुपात के बराबर है te से te की ज्या, जिसका अर्थ है कि कोटैंजेंट का वर्ग te की कोज्या के वर्ग और te की ज्या के वर्ग का अनुपात है।
टी के साइन वर्ग से घटाने के बाद, हमें टी के वर्ग की इकाई और कोसाइन के बीच का अंतर मिलता है, जो टी के वर्ग की साइन के बराबर है)। क्यू.ई.डी.

उदाहरण 4. यदि tgt + ctgt = 6 है तो व्यंजक tg 2 t + ctg 2 t का मान ज्ञात कीजिए।
(टी की स्पर्शरेखा और टे के कोटैंजेंट के वर्गों का योग, यदि स्पर्शरेखा और कोटैंजेंट का योग छह है)।
समाधान। (टीजीटी + सीटीजीटी) 2 = 6 2
टीजी 2 टी + 2 ∙ टीजीटी ∙सीटीजीटी + सीटीजी 2 टी = 36
टीजी 2 टी + 2 + सीटीजी 2 टी = 36
टीजी 2 टी + सीटीजी 2 टी = 36-2
टीजी 2 टी + सीटीजी 2 टी = 34
आइए मूल समानता के दोनों भागों का वर्ग करें:
(tgt + ctgt) 2 = 6 2 (te की स्पर्शरेखा और te की स्पर्शरेखा के योग का वर्ग छह वर्ग है)। संक्षिप्त गुणन सूत्र को याद करें: दो मात्राओं के योग का वर्ग पहले के वर्ग के बराबर होता है और पहले और दूसरे के गुणनफल के दोगुने के बराबर होता है। (a+b) 2 =a 2 +2ab+b 2 हमें tg 2 t + 2 ∙ tgt ∙ctgt + ctg 2 t = 36 मिलता है।

चूँकि te की स्पर्शरेखा और te के कोटैंजेंट का गुणनफल एक के बराबर है, तो tg 2 t + 2 + ctg 2 t \u003d 36 (te की स्पर्शरेखा और te और दो के कोटैंजेंट के वर्गों का योग है) छत्तीस),
वोरोनकोवा ओल्गा इवानोव्ना
एमबीओयू "माध्यमिक विद्यालय
नंबर 18"
एंगेल्स, सेराटोव क्षेत्र।
गणित शिक्षक.
"त्रिकोणमितीय अभिव्यक्ति और उनके परिवर्तन"
परिचय ………………………………………………………………..3
अध्याय 1 त्रिकोणमितीय अभिव्यक्तियों के परिवर्तनों के उपयोग के लिए कार्यों का वर्गीकरण ……………………….……………………5
1.1. गणना कार्य त्रिकोणमितीय व्यंजकों का मान……….5
1.2.त्रिकोणमितीय व्यंजकों को सरल बनाने के कार्य.... 7
1.3. संख्यात्मक त्रिकोणमितीय अभिव्यक्तियों के रूपांतरण के लिए कार्य… ..7
1.4 मिश्रित कार्य……………………………………………………9
अध्याय दो
2.1 ग्रेड 10 में विषयगत पुनरावृत्ति……………………………………11
परीक्षण 1…………………………………………………………………….12
टेस्ट 2……………………………………………………………………..13
टेस्ट 3……………………………………………………………………..14
2.2 ग्रेड 11 में अंतिम पुनरावृत्ति…………………………………………15
परीक्षण 1……………………………………………………………………..17
परीक्षण 2……………………………………………………………………..17
टेस्ट 3……………………………………………………………………..18
निष्कर्ष…………………………………………………………………………19
प्रयुक्त साहित्य की सूची………………………………………….20
परिचय।
आज की परिस्थितियों में, सबसे महत्वपूर्ण प्रश्न यह है: "हम छात्रों के ज्ञान में कुछ कमियों को दूर करने में कैसे मदद कर सकते हैं और उन्हें परीक्षा में संभावित गलतियों के प्रति आगाह कर सकते हैं?" इस मुद्दे को हल करने के लिए, छात्रों से कार्यक्रम सामग्री को औपचारिक रूप से आत्मसात करना नहीं, बल्कि इसकी गहरी और सचेत समझ, मौखिक गणना और परिवर्तनों की गति का विकास, साथ ही सबसे सरल को हल करने के लिए कौशल का विकास करना आवश्यक है। समस्याएँ "मन में"। छात्रों को यह विश्वास दिलाना आवश्यक है कि केवल गणित के अध्ययन में सक्रिय स्थिति की उपस्थिति में, व्यावहारिक कौशल, कौशल के अधिग्रहण और उनके उपयोग के अधीन, कोई वास्तविक सफलता पर भरोसा कर सकता है। कक्षा 10-11 में वैकल्पिक विषयों सहित परीक्षा की तैयारी के लिए हर अवसर का उपयोग करना, छात्रों के साथ जटिल कार्यों का नियमित रूप से विश्लेषण करना, कक्षा और अतिरिक्त कक्षाओं में उन्हें हल करने का सबसे तर्कसंगत तरीका चुनना आवश्यक है।में सकारात्मक परिणामयदि गणित शिक्षक, सृजन करके विशिष्ट समस्याओं को हल करने का क्षेत्र प्राप्त कर सकते हैंछात्रों का अच्छा बुनियादी प्रशिक्षण, हमारे सामने आने वाली समस्याओं को हल करने के नए तरीकों की तलाश करना, सक्रिय रूप से प्रयोग करना, आधुनिक शैक्षणिक प्रौद्योगिकियों, विधियों, तकनीकों को लागू करना जो छात्रों के प्रभावी आत्म-प्राप्ति और आत्मनिर्णय के लिए अनुकूल परिस्थितियों का निर्माण करते हैं। नई सामाजिक स्थितियाँ.
त्रिकोणमिति स्कूली गणित पाठ्यक्रम का एक अभिन्न अंग है। त्रिकोणमिति में अच्छा ज्ञान और मजबूत कौशल गणितीय संस्कृति के पर्याप्त स्तर का प्रमाण है, जो गणित, भौतिकी और कई तकनीकी के सफल अध्ययन के लिए एक अनिवार्य शर्त है।अनुशासन.
कार्य की प्रासंगिकता. स्कूली स्नातकों का एक महत्वपूर्ण हिस्सा गणित के इस महत्वपूर्ण खंड में साल-दर-साल बहुत खराब तैयारी दिखाता है, जैसा कि उत्तीर्ण होने के विश्लेषण के बाद से पिछले वर्षों के परिणामों (2011-48.41%, 2012-51.05%) के परिणामों से प्रमाणित है। एकीकृत राज्य परीक्षा से पता चला कि छात्र इस विशेष अनुभाग के असाइनमेंट को पूरा करते समय कई गलतियाँ करते हैं या ऐसे असाइनमेंट बिल्कुल भी नहीं करते हैं। एक में त्रिकोणमिति में राज्य परीक्षा के प्रश्न लगभग तीन प्रकार के कार्यों में पाए जाते हैं। यह कार्य B5 में सबसे सरल त्रिकोणमितीय समीकरणों का समाधान है, और कार्य B7 में त्रिकोणमितीय अभिव्यक्तियों के साथ काम करता है, और कार्य B14 में त्रिकोणमितीय कार्यों का अध्ययन, साथ ही कार्य B12, जिसमें भौतिक घटनाओं का वर्णन करने वाले और त्रिकोणमितीय कार्यों वाले सूत्र हैं . और यह कार्य बी का केवल एक हिस्सा है! लेकिन मूल C1 के चयन के साथ पसंदीदा त्रिकोणमितीय समीकरण भी हैं, और "बहुत पसंदीदा नहीं" ज्यामितीय कार्य C2 और C4 भी हैं।
कार्य का लक्ष्य. त्रिकोणमितीय अभिव्यक्तियों के परिवर्तन के लिए समर्पित USE कार्यों B7 की सामग्री का विश्लेषण करें और परीक्षणों में उनकी प्रस्तुति के रूप के अनुसार कार्यों को वर्गीकृत करें।
कार्य में दो अध्याय हैं, परिचय और निष्कर्ष। परिचय कार्य की प्रासंगिकता पर जोर देता है। पहला अध्याय एकीकृत राज्य परीक्षा (2012) के परीक्षण कार्यों में त्रिकोणमितीय अभिव्यक्तियों के परिवर्तनों के उपयोग के लिए कार्यों का वर्गीकरण प्रदान करता है।
दूसरे अध्याय में, ग्रेड 10, 11 में "त्रिकोणमितीय अभिव्यक्तियों का परिवर्तन" विषय की पुनरावृत्ति के संगठन पर विचार किया गया है और इस विषय पर परीक्षण विकसित किए गए हैं।
संदर्भों की सूची में 17 स्रोत शामिल हैं।
अध्याय 1. त्रिकोणमितीय अभिव्यक्तियों के परिवर्तनों के उपयोग के लिए कार्यों का वर्गीकरण।
माध्यमिक (पूर्ण) शिक्षा के मानक और छात्रों के प्रशिक्षण के स्तर की आवश्यकताओं के अनुसार, त्रिकोणमिति की मूल बातें जानने के कार्यों को आवश्यकताओं के कोडिफायर में शामिल किया गया है।
त्रिकोणमिति की मूल बातें सीखना सबसे प्रभावी होगा जब:
छात्रों को पहले से अध्ययन की गई सामग्री को दोहराने के लिए सकारात्मक रूप से प्रेरित किया जाएगा;
शैक्षिक प्रक्रिया में छात्र-केंद्रित दृष्टिकोण लागू किया जाएगा;
कार्यों की एक प्रणाली लागू की जाएगी जो छात्रों के ज्ञान के विस्तार, गहनता, व्यवस्थितकरण में योगदान करेगी;
उन्नत शैक्षणिक प्रौद्योगिकियों का उपयोग किया जाएगा।
परीक्षा की तैयारी के लिए साहित्य और इंटरनेट संसाधनों का विश्लेषण करने के बाद, हमने कार्यों B7 (KIM USE 2012-त्रिकोणमिति) के संभावित वर्गीकरणों में से एक का प्रस्ताव दिया है: गणना के लिए कार्यत्रिकोणमितीय अभिव्यक्तियों के मूल्य; के लिए असाइनमेंटसंख्यात्मक त्रिकोणमितीय अभिव्यक्तियों का रूपांतरण; शाब्दिक त्रिकोणमितीय अभिव्यक्तियों के परिवर्तन के लिए कार्य; मिश्रित कार्य.
1.1. गणना कार्य त्रिकोणमितीय अभिव्यक्तियों के मान.
सरल त्रिकोणमिति समस्याओं के सबसे आम प्रकारों में से एक उनमें से किसी एक के मूल्य द्वारा त्रिकोणमितीय कार्यों के मूल्यों की गणना है:
ए) मूल त्रिकोणमितीय पहचान और उसके परिणामों का उपयोग।
उदाहरण 1
. यदि खोजें  और
और  .
.
समाधान।  ,
,  ,
,
क्योंकि , वह  .
.
उत्तर।
उदाहरण 2
. खोजो  , अगर
, अगर  और ।
और ।
समाधान।  ,
,  ,
,  .
.
क्योंकि , वह  .
.
उत्तर। .
ख) द्विकोण सूत्रों का उपयोग।
उदाहरण 3
. खोजो  , अगर
, अगर  .
.
समाधान। ,  .
.
उत्तर।  .
.
उदाहरण 4
. किसी व्यंजक का मान ज्ञात कीजिए  .
.
समाधान। .
उत्तर।  .
.
1. खोजो , अगर
 और
और  . उत्तर। -0.2
. उत्तर। -0.2 2.
खोजो , अगर  और
और  . उत्तर। 0.4
. उत्तर। 0.4
 , अगर । उत्तर। -12.884.
खोजो
, अगर । उत्तर। -12.884.
खोजो  , अगर
, अगर  . उत्तर। -0.845.
अभिव्यक्ति का मान ज्ञात कीजिए:
. उत्तर। -0.845.
अभिव्यक्ति का मान ज्ञात कीजिए: . उत्तर। 66.
किसी व्यंजक का मान ज्ञात कीजिए
. उत्तर। 66.
किसी व्यंजक का मान ज्ञात कीजिए .उत्तर। -19
.उत्तर। -191.2.त्रिकोणमितीय व्यंजकों को सरल बनाने के कार्य। कटौती के सूत्रों में छात्रों को अच्छी तरह से महारत हासिल होनी चाहिए, क्योंकि आगे उनका उपयोग ज्यामिति, भौतिकी और अन्य संबंधित विषयों के पाठों में किया जाएगा।
उदाहरण 5
.
भावों को सरल बनाएं  .
.
समाधान। .
उत्तर।  .
.
स्वतंत्र समाधान के लिए कार्य:
1. अभिव्यक्ति को सरल कीजिये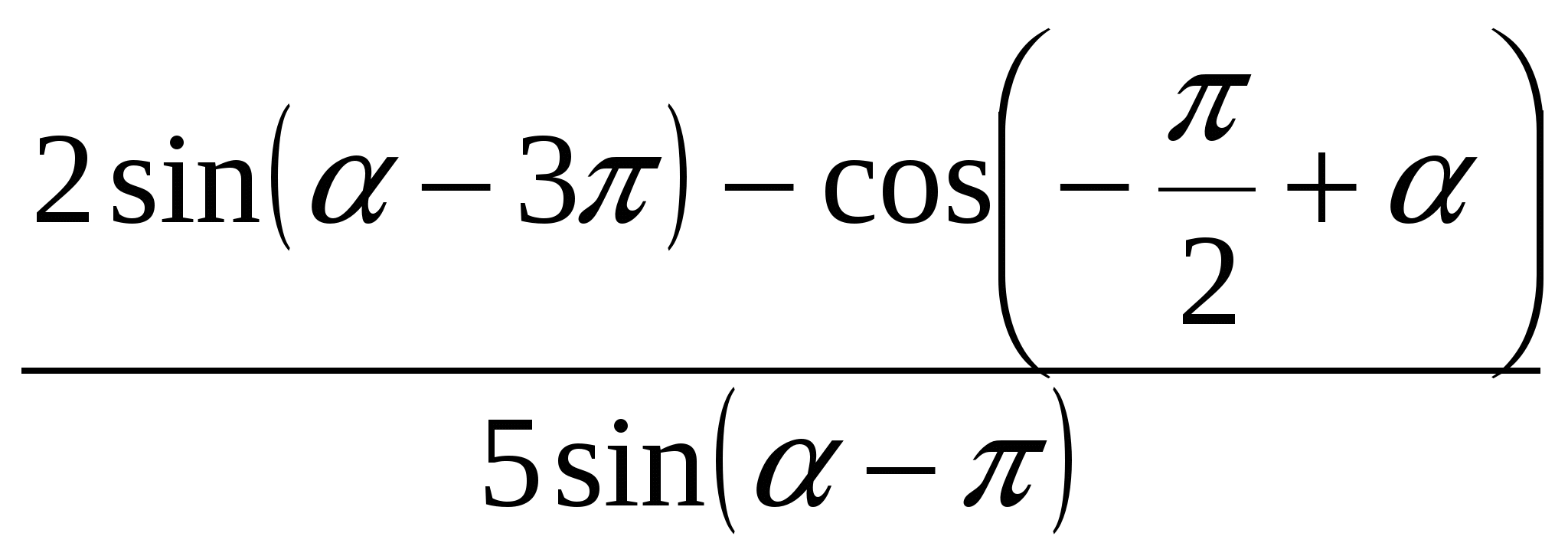 .
उत्तर। 0.62.
खोजो
.
उत्तर। 0.62.
खोजो  , अगर
, अगर  और. उत्तर। 10.563.
किसी व्यंजक का मान ज्ञात कीजिए
और. उत्तर। 10.563.
किसी व्यंजक का मान ज्ञात कीजिए  , अगर
, अगर  .
उत्तर। 2
.
उत्तर। 2 1.3. संख्यात्मक त्रिकोणमितीय अभिव्यक्तियों के परिवर्तन के लिए कार्य।
संख्यात्मक त्रिकोणमितीय अभिव्यक्तियों को परिवर्तित करने के लिए कार्यों के कौशल और क्षमताओं को विकसित करते समय, त्रिकोणमितीय कार्यों के मूल्यों की तालिका, समता के गुणों और त्रिकोणमितीय कार्यों की आवधिकता के ज्ञान पर ध्यान दिया जाना चाहिए।
a) कुछ कोणों के लिए त्रिकोणमितीय फलनों के सटीक मानों का उपयोग करना।
उदाहरण 6
. गणना  .
.
समाधान।  .
.
उत्तर।  .
.
बी) समता के गुणों का उपयोग करना त्रिकोणमितीय कार्य।
उदाहरण 7
. गणना  .
.
समाधान। .
उत्तर। 
वी) आवधिकता गुणों का उपयोग करनात्रिकोणमितीय कार्य।
उदाहरण 8
.
किसी व्यंजक का मान ज्ञात कीजिए  .
.
समाधान। .
उत्तर।  .
.
स्वतंत्र समाधान के लिए कार्य:
1. किसी व्यंजक का मान ज्ञात कीजिए .
उत्तर। -40.52. व्यंजक का मान ज्ञात कीजिए
.
उत्तर। -40.52. व्यंजक का मान ज्ञात कीजिए  .
उत्तर। 17
.
उत्तर। 17 3.
किसी व्यंजक का मान ज्ञात कीजिए  .
उत्तर। 6
.
उत्तर। 6
 .
उत्तर। -24
.
उत्तर। -24  उत्तर। -64
उत्तर। -641.4 मिश्रित कार्य.
प्रमाणीकरण के परीक्षण प्रपत्र में बहुत महत्वपूर्ण विशेषताएं हैं, इसलिए एक ही समय में कई त्रिकोणमितीय सूत्रों के उपयोग से जुड़े कार्यों पर ध्यान देना महत्वपूर्ण है।
उदाहरण 9
खोजो  , अगर
, अगर  .
.
समाधान।  .
.
उत्तर।  .
.
उदाहरण 10
. खोजो  , अगर
, अगर  और
और  .
.
समाधान। .
क्योंकि , वह  .
.
उत्तर।  .
.
उदाहरण 11.
खोजो  , अगर ।
, अगर ।
समाधान। , ,  ,
,  ,
,  ,
,  ,
,  .
.
उत्तर।
उदाहरण 12.
गणना  .
.
समाधान। .
उत्तर।  .
.
उदाहरण 13
किसी व्यंजक का मान ज्ञात कीजिए  , अगर
, अगर  .
.
समाधान। .
उत्तर।  .
.
स्वतंत्र समाधान के लिए कार्य:
1. खोजो , अगर
, अगर  .
उत्तर। -1.75
.
उत्तर। -1.752. खोजो
 , अगर
, अगर  .
उत्तर। 33. खोजें
.
उत्तर। 33. खोजें  , अगर ।उत्तर। 0.254. व्यंजक का मान ज्ञात कीजिए
, अगर ।उत्तर। 0.254. व्यंजक का मान ज्ञात कीजिए  , अगर
, अगर  .
उत्तर। 0.35. व्यंजक का मान ज्ञात कीजिए
.
उत्तर। 0.35. व्यंजक का मान ज्ञात कीजिए  , अगर
, अगर  .
उत्तर। 5
.
उत्तर। 5अध्याय 2. "त्रिकोणमितीय अभिव्यक्तियों का परिवर्तन" विषय की अंतिम पुनरावृत्ति के संगठन के पद्धतिगत पहलू।
शैक्षणिक प्रदर्शन को और बेहतर बनाने, छात्रों के बीच गहन और ठोस ज्ञान की उपलब्धि में योगदान देने वाले सबसे महत्वपूर्ण मुद्दों में से एक पहले से अध्ययन की गई सामग्री को दोहराने का मुद्दा है। अभ्यास से पता चलता है कि 10वीं कक्षा में विषयगत पुनरावृत्ति को व्यवस्थित करना अधिक समीचीन है; 11वीं कक्षा में - अंतिम पुनरावृत्ति।
2.1. 10वीं कक्षा में विषयगत पुनरावृत्ति।
गणितीय सामग्री पर काम करने की प्रक्रिया में, प्रत्येक पूर्ण विषय या पाठ्यक्रम के पूरे खंड की पुनरावृत्ति विशेष रूप से महत्वपूर्ण हो जाती है।
विषयगत दोहराव के साथ, विषय पर छात्रों के ज्ञान को इसके पारित होने के अंतिम चरण में या ब्रेक के बाद व्यवस्थित किया जाता है।
विषयगत पुनरावृत्ति के लिए, विशेष पाठ आवंटित किए जाते हैं, जिस पर एक विशेष विषय की सामग्री केंद्रित और सामान्यीकृत होती है।
इस वार्तालाप में छात्रों की व्यापक भागीदारी के साथ बातचीत के माध्यम से पाठ में पुनरावृत्ति की जाती है। उसके बाद, छात्रों को एक निश्चित विषय को दोहराने का कार्य दिया जाता है और चेतावनी दी जाती है कि परीक्षणों पर क्रेडिट कार्य होगा।
किसी विषय पर एक परीक्षण में उसके सभी मुख्य प्रश्न शामिल होने चाहिए। कार्य पूरा होने के बाद, विशिष्ट त्रुटियों का विश्लेषण किया जाता है और उन्हें खत्म करने के लिए पुनरावृत्ति का आयोजन किया जाता है।
विषयगत पुनरावृत्ति के पाठों के लिए, हम विकसित की पेशकश करते हैं परीक्षण पत्र"त्रिकोणमितीय अभिव्यक्तियों का रूपांतरण" विषय पर।
परीक्षण #1
परीक्षण #2
परीक्षण #3
उत्तर तालिका
परीक्षा
2.2. 11वीं कक्षा में अंतिम पुनरावृत्ति।
अंतिम पुनरावृत्ति गणित पाठ्यक्रम के मुख्य मुद्दों के अध्ययन के अंतिम चरण में की जाती है और इस खंड या संपूर्ण पाठ्यक्रम के लिए शैक्षिक सामग्री के अध्ययन के साथ तार्किक संबंध में की जाती है।
शैक्षिक सामग्री की अंतिम पुनरावृत्ति के निम्नलिखित लक्ष्य हैं:
1. इसकी तार्किक संरचना को स्पष्ट करने और विषय और अंतर विषय संबंधों के भीतर एक प्रणाली बनाने के लिए संपूर्ण प्रशिक्षण पाठ्यक्रम की सामग्री को सक्रिय करना।
2. पुनरावृत्ति की प्रक्रिया में पाठ्यक्रम के मुख्य मुद्दों पर छात्रों के ज्ञान को गहरा करना और यदि संभव हो तो उसका विस्तार करना।
सभी स्नातकों के लिए गणित में अनिवार्य परीक्षा के संदर्भ में, यूएसई की क्रमिक शुरूआत शिक्षकों को पाठों की तैयारी और संचालन के लिए एक नया दृष्टिकोण अपनाने में मदद करती है, यह सुनिश्चित करने की आवश्यकता को ध्यान में रखते हुए कि सभी छात्र बुनियादी स्तर पर शैक्षिक सामग्री में निपुण हों, साथ ही विश्वविद्यालय में प्रवेश के लिए उच्च अंक प्राप्त करने में रुचि रखने वाले प्रेरित छात्रों के लिए अवसर, उच्च और उच्च स्तर पर सामग्री में महारत हासिल करने में गतिशील प्रगति।
अंतिम पुनरावृत्ति के पाठों में, आप निम्नलिखित कार्यों पर विचार कर सकते हैं:
उदाहरण 1 . अभिव्यक्ति के मान की गणना करें।समाधान। = = =
= =  =
= =
= =
= =0,5.
उत्तर। 0.5. उदाहरण 2
वह सबसे बड़ा पूर्णांक मान निर्दिष्ट करें जो अभिव्यक्ति ले सकता है
=0,5.
उत्तर। 0.5. उदाहरण 2
वह सबसे बड़ा पूर्णांक मान निर्दिष्ट करें जो अभिव्यक्ति ले सकता है  .
.
समाधान। क्योंकि  खंड से संबंधित कोई भी मूल्य ले सकता है [-1; 1], फिर
खंड से संबंधित कोई भी मूल्य ले सकता है [-1; 1], फिर  खंड का कोई भी मान लेता है [–0.4; 0.4], इसलिए। व्यंजक का पूर्णांक मान एक है - संख्या 4.
खंड का कोई भी मान लेता है [–0.4; 0.4], इसलिए। व्यंजक का पूर्णांक मान एक है - संख्या 4.
 .
.
समाधान: आइए घनों के योग का गुणनखंड करने के लिए सूत्र का उपयोग करें:। हमारे पास है
हमारे पास है:  .
.
उत्तर 1
उदाहरण 4
गणना  .
.
समाधान। .
उत्तर: 0.28
अंतिम पुनरावृत्ति के पाठों के लिए, हम "त्रिकोणमितीय अभिव्यक्तियों का रूपांतरण" विषय पर विकसित परीक्षण प्रदान करते हैं।
सबसे बड़ा पूर्णांक निर्दिष्ट करें जो 1 से अधिक न हो
निष्कर्ष.
इस विषय पर प्रासंगिक पद्धति संबंधी साहित्य पर काम करने के बाद, हम यह निष्कर्ष निकाल सकते हैं कि स्कूली गणित पाठ्यक्रम में त्रिकोणमितीय परिवर्तनों से संबंधित कार्यों को हल करने की क्षमता और कौशल बहुत महत्वपूर्ण हैं।
किए गए कार्य के दौरान, कार्यों का वर्गीकरण B7 किया गया। 2012 के सीएमएम में सबसे अधिक उपयोग किए जाने वाले त्रिकोणमितीय सूत्रों पर विचार किया गया है। समाधान वाले कार्यों के उदाहरण दिए गए हैं. परीक्षा की तैयारी में ज्ञान की पुनरावृत्ति और व्यवस्थितकरण को व्यवस्थित करने के लिए विभेदक परीक्षण विकसित किए गए हैं।
विचार करते हुए शुरू किए गए कार्य को जारी रखना उचित है कार्य B5 में सरलतम त्रिकोणमितीय समीकरणों का समाधान, कार्य B14 में त्रिकोणमितीय कार्यों का अध्ययन, कार्य B12, जिसमें भौतिक घटनाओं का वर्णन करने वाले और त्रिकोणमितीय कार्यों वाले सूत्र हैं।
अंत में, मैं यह नोट करना चाहूंगा कि परीक्षा उत्तीर्ण करने की प्रभावशीलता काफी हद तक इस बात से निर्धारित होती है कि शिक्षा के सभी स्तरों पर, सभी श्रेणियों के छात्रों के साथ तैयारी प्रक्रिया कितनी प्रभावी ढंग से आयोजित की जाती है। और यदि हम छात्रों में उनके अगले जीवन भर सीखने की स्वतंत्रता, जिम्मेदारी और तत्परता का निर्माण करने का प्रबंधन करते हैं, तो हम न केवल राज्य और समाज के आदेश को पूरा करेंगे, बल्कि अपने स्वयं के आत्म-सम्मान को भी बढ़ाएंगे।
शैक्षिक सामग्री की पुनरावृत्ति के लिए शिक्षक से रचनात्मक कार्य की आवश्यकता होती है। उसे दोहराव के प्रकारों के बीच एक स्पष्ट संबंध प्रदान करना होगा, दोहराव की गहराई से सोची-समझी प्रणाली लागू करनी होगी। दोहराव को व्यवस्थित करने की कला में महारत हासिल करना शिक्षक का कार्य है। छात्रों के ज्ञान की मजबूती काफी हद तक इसके समाधान पर निर्भर करती है।
साहित्य।
वायगोडस्की हां.या., प्रारंभिक गणित की पुस्तिका। -एम.: नौका, 1970.
बीजगणित में बढ़ी हुई कठिनाई के कार्य और विश्लेषण की शुरुआत: हाई स्कूल / बी.एम. के 10-11 ग्रेड के लिए पाठ्यपुस्तक। इवलेव, ए.एम. अब्रामोव, यू.पी. डुडनित्सिन, एस.आई. श्वार्जबर्ड. - एम.: ज्ञानोदय, 1990।
भावों के परिवर्तन के लिए बुनियादी त्रिकोणमितीय सूत्रों का अनुप्रयोग (ग्रेड 10) // शैक्षणिक विचारों का उत्सव। 2012-2013.
कोर्यानोव ए.जी. , प्रोकोफ़िएव ए.ए. हम परीक्षा के लिए अच्छे छात्रों और उत्कृष्ट छात्रों को तैयार करते हैं। - एम.: पेडागोगिकल यूनिवर्सिटी "फर्स्ट ऑफ सितंबर", 2012.- 103 पी।
कुज़नेत्सोवा ई.एन.त्रिकोणमितीय व्यंजकों का सरलीकरण. विभिन्न विधियों द्वारा त्रिकोणमितीय समीकरणों को हल करना (परीक्षा की तैयारी)। 11th ग्रेड। 2012-2013.
कुलनिन ई.डी. गणित में 3000 प्रतिस्पर्धी समस्याएं। चौथी आईडी., सही. और अतिरिक्त - एम.: रॉल्फ, 2000.
मोर्दकोविच ए.जी. एक सामान्य शिक्षा स्कूल में त्रिकोणमिति का अध्ययन करने की पद्धतिगत समस्याएं // स्कूल में गणित। 2002. नंबर 6.
पिचुरिन एल.एफ. त्रिकोणमिति के बारे में और न केवल इसके बारे में: -एम। आत्मज्ञान, 1985
रेशेतनिकोव एन.एन. स्कूल में त्रिकोणमिति:-एम. : शैक्षणिक विश्वविद्यालय "सितंबर का पहला", 2006, एलके 1।
शबुनिन एम.आई., प्रोकोफिव ए.ए. अंक शास्त्र। बीजगणित. गणितीय विश्लेषण की शुरुआत। प्रोफाइल स्तर: ग्रेड 10 के लिए पाठ्यपुस्तक - एम।: बिनोम। नॉलेज लैब, 2007।
परीक्षा की तैयारी के लिए शैक्षिक पोर्टल।
गणित में परीक्षा की तैयारी "ओह, यह त्रिकोणमिति! http://festival.1september.ru/articles/621971/
प्रोजेक्ट "गणित? आसान!!!" http://www.resolventa.ru/
अनुभाग: अंक शास्त्र
कक्षा: 11
पाठ 1
विषय: ग्रेड 11 (परीक्षा की तैयारी)
त्रिकोणमितीय व्यंजकों का सरलीकरण.
सरलतम त्रिकोणमितीय समीकरणों का समाधान. (2 घंटे)
लक्ष्य:
- त्रिकोणमिति सूत्रों के उपयोग और सरलतम त्रिकोणमितीय समीकरणों के समाधान से संबंधित छात्रों के ज्ञान और कौशल को व्यवस्थित, सामान्यीकृत, विस्तारित करें।
पाठ के लिए उपकरण:
पाठ संरचना:
- ऑर्गमोमेंट
- लैपटॉप पर परीक्षण. नतीजों की चर्चा.
- त्रिकोणमितीय व्यंजकों को सरल बनाना
- सरलतम त्रिकोणमितीय समीकरणों का समाधान
- स्वतंत्र काम।
- पाठ का सारांश. गृहकार्य की व्याख्या.
1. आयोजन का क्षण. (दो मिनट।)
शिक्षक दर्शकों का स्वागत करता है, पाठ के विषय की घोषणा करता है, याद दिलाता है कि पहले त्रिकोणमिति सूत्रों को दोहराने का कार्य दिया गया था और छात्रों को परीक्षण के लिए तैयार किया गया था।
2. परीक्षण. (15 मिनट + 3 मिनट की चर्चा)
लक्ष्य त्रिकोणमितीय सूत्रों के ज्ञान और उन्हें लागू करने की क्षमता का परीक्षण करना है। प्रत्येक छात्र के डेस्क पर एक लैपटॉप होता है जिसमें परीक्षण का विकल्प होता है।
कई विकल्प हो सकते हैं, मैं उनमें से एक का उदाहरण दूंगा:
मैं विकल्प.
भावों को सरल बनाएं:
ए) बुनियादी त्रिकोणमितीय पहचान
1. पाप 2 3y + cos 2 3y + 1;
बी) अतिरिक्त सूत्र
3. पाप5x - पाप3x;
ग) किसी उत्पाद को योग में परिवर्तित करना
6. 2sin8y cos3y;
घ) द्विकोण सूत्र
7.2sin5x cos5x;
ई) अर्धकोण सूत्र
च) त्रिकोण सूत्र
छ) सार्वभौमिक प्रतिस्थापन
ज) डिग्री कम करना
16. कॉस 2 (3x/7);
प्रत्येक फार्मूले के सामने छात्र लैपटॉप पर अपना उत्तर देखते हैं।
कार्य की जाँच कम्प्यूटर द्वारा तुरन्त की जाती है। परिणाम सभी के देखने के लिए बड़ी स्क्रीन पर प्रदर्शित किए जाते हैं।
साथ ही, काम खत्म होने के बाद सही उत्तर छात्रों के लैपटॉप पर दिखाए जाते हैं। प्रत्येक छात्र यह देखता है कि गलती कहां हुई है और उसे कौन से फॉर्मूले दोहराने की जरूरत है।
3. त्रिकोणमितीय व्यंजकों का सरलीकरण। (25 मि.)
लक्ष्य त्रिकोणमिति के बुनियादी सूत्रों के अनुप्रयोग को दोहराना, काम करना और समेकित करना है। परीक्षा से समस्या B7 का समाधान।
इस स्तर पर, कक्षा को मजबूत (बाद में सत्यापन के साथ स्वतंत्र रूप से काम करें) और शिक्षक के साथ काम करने वाले कमजोर छात्रों के समूहों में विभाजित करने की सलाह दी जाती है।
मजबूत छात्रों के लिए असाइनमेंट (मुद्रित आधार पर पहले से तैयार)। USE 2011 के अनुसार, मुख्य जोर कटौती और दोहरे कोण फ़ार्मुलों पर है।
अभिव्यक्ति को सरल बनाएं (मजबूत शिक्षार्थियों के लिए):

समानांतर में, शिक्षक कमजोर छात्रों के साथ काम करता है, छात्रों के निर्देशन में स्क्रीन पर कार्यों पर चर्चा करता है और उन्हें हल करता है।
गणना करें:
5) पाप(270º - α) + cos(270º + α)
6) 
सरल बनाएं:

अब बारी थी सशक्त समूह के कार्य के परिणामों पर चर्चा की।
उत्तर स्क्रीन पर दिखाई देते हैं, और साथ ही, एक वीडियो कैमरे की मदद से, 5 अलग-अलग छात्रों का काम प्रदर्शित होता है (प्रत्येक के लिए एक कार्य)।
निर्बल समूह परिस्थिति एवं समाधान विधि को देखता है। चर्चा और विश्लेषण होता है. तकनीकी साधनों के प्रयोग से यह शीघ्रता से होता है।
4. सरलतम त्रिकोणमितीय समीकरणों का समाधान। (30 मिनट।)
लक्ष्य सरलतम त्रिकोणमितीय समीकरणों के समाधान को दोहराना, व्यवस्थित करना और सामान्यीकृत करना, उनकी जड़ों को रिकॉर्ड करना है। समस्या B3 का समाधान.
कोई भी त्रिकोणमितीय समीकरण, चाहे हम उसे कैसे भी हल करें, सबसे सरल की ओर ले जाता है।
कार्य पूरा करते समय, छात्रों को विशेष मामलों के समीकरणों की जड़ों को सामान्य रूप में लिखने और अंतिम समीकरण में जड़ों के चयन पर ध्यान देना चाहिए।
समीकरण हल करें:

उत्तर का सबसे छोटा सकारात्मक मूल लिखिए।
5. स्वतंत्र कार्य (10 मिनट)
लक्ष्य अर्जित कौशल का परीक्षण करना, समस्याओं, त्रुटियों की पहचान करना और उन्हें खत्म करने के तरीकों की पहचान करना है।
छात्र की पसंद पर विभिन्न प्रकार के काम की पेशकश की जाती है।
"3" के लिए विकल्प
1) व्यंजक का मान ज्ञात कीजिए ![]()
2) अभिव्यक्ति 1 - पाप 2 3α - कॉस 2 3α को सरल बनाएं
3) समीकरण हल करें ![]()
"4" के लिए विकल्प
1) व्यंजक का मान ज्ञात कीजिए
2) समीकरण हल करें ![]() अपने उत्तर का सबसे छोटा सकारात्मक मूल लिखिए।
अपने उत्तर का सबसे छोटा सकारात्मक मूल लिखिए।
"5" के लिए विकल्प
1) यदि tgα ज्ञात करें ![]()
2) समीकरण का मूल ज्ञात कीजिए ![]() अपने उत्तर का सबसे छोटा सकारात्मक मूल लिखिए।
अपने उत्तर का सबसे छोटा सकारात्मक मूल लिखिए।
6. पाठ का सारांश (5 मिनट)
शिक्षक ने इस तथ्य का सारांश दिया कि पाठ में त्रिकोणमितीय सूत्रों को दोहराया और समेकित किया गया, सबसे सरल त्रिकोणमितीय समीकरणों का समाधान।
अगले पाठ में मौके की जांच के साथ गृहकार्य (पहले से मुद्रित आधार पर तैयार) सौंपा जाता है।
समीकरण हल करें:

9) ![]()
10) ![]() अपना उत्तर सबसे छोटे सकारात्मक मूल के रूप में दें।
अपना उत्तर सबसे छोटे सकारात्मक मूल के रूप में दें।
पाठ 2
विषय: ग्रेड 11 (परीक्षा की तैयारी)
त्रिकोणमितीय समीकरणों को हल करने की विधियाँ। जड़ चयन. (2 घंटे)
लक्ष्य:
- विभिन्न प्रकार के त्रिकोणमितीय समीकरणों को हल करने पर ज्ञान को सामान्य बनाना और व्यवस्थित करना।
- छात्रों की गणितीय सोच, निरीक्षण करने, तुलना करने, सामान्यीकरण करने, वर्गीकृत करने की क्षमता के विकास को बढ़ावा देना।
- छात्रों को मानसिक गतिविधि की प्रक्रिया में कठिनाइयों को दूर करने, आत्म-नियंत्रण, अपनी गतिविधियों का आत्मनिरीक्षण करने के लिए प्रोत्साहित करें।
पाठ के लिए उपकरण:केआरएमयू, प्रत्येक छात्र के लिए लैपटॉप।
पाठ संरचना:
- ऑर्गमोमेंट
- चर्चा डी/एस एवं समोट। अंतिम पाठ का कार्य
- त्रिकोणमितीय समीकरणों को हल करने की विधियों की पुनरावृत्ति।
- त्रिकोणमितीय समीकरणों को हल करना
- त्रिकोणमितीय समीकरणों में मूलों का चयन.
- स्वतंत्र काम।
- पाठ का सारांश. गृहकार्य।
1. आयोजन का क्षण (2 मिनट)
शिक्षक दर्शकों का स्वागत करता है, पाठ के विषय और कार्य योजना की घोषणा करता है।
2.ए) होमवर्क का विश्लेषण (5 मिनट)
लक्ष्य प्रदर्शन की जाँच करना है. वीडियो कैमरे की सहायता से एक कार्य को स्क्रीन पर प्रदर्शित किया जाता है, बाकी को शिक्षक द्वारा जांचने के लिए चुनिंदा रूप से एकत्र किया जाता है।
बी) स्वतंत्र कार्य का विश्लेषण (3 मिनट)
लक्ष्य गलतियों को सुलझाना, उन्हें दूर करने के उपाय बताना है।
स्क्रीन पर उत्तर और समाधान हैं, छात्रों ने अपना काम पहले ही जारी कर दिया है। विश्लेषण तेजी से चल रहा है.
3. त्रिकोणमितीय समीकरणों को हल करने की विधियों की पुनरावृत्ति (5 मिनट)
लक्ष्य त्रिकोणमितीय समीकरणों को हल करने के तरीकों को याद करना है।
विद्यार्थियों से पूछें कि वे त्रिकोणमितीय समीकरणों को हल करने की कौन सी विधियाँ जानते हैं। इस बात पर ज़ोर दें कि तथाकथित बुनियादी (अक्सर उपयोग की जाने वाली) विधियाँ हैं:
- परिवर्तनीय प्रतिस्थापन,
- गुणनखंडन,
- सजातीय समीकरण,
और लागू तरीके हैं:
- किसी राशि को उत्पाद में और उत्पाद को राशि में बदलने के फ़ार्मुलों के अनुसार,
- कमी सूत्रों द्वारा,
- सार्वभौमिक त्रिकोणमितीय प्रतिस्थापन
- एक सहायक कोण का परिचय,
- किसी त्रिकोणमितीय फलन द्वारा गुणन।
यह भी याद रखना चाहिए कि एक समीकरण को विभिन्न तरीकों से हल किया जा सकता है।
4. त्रिकोणमितीय समीकरण हल करना (30 मिनट)
लक्ष्य इस विषय पर ज्ञान और कौशल को सामान्य बनाना और समेकित करना है, ताकि यूएसई से सी1 को हल करने की तैयारी की जा सके।
मैं छात्रों के साथ मिलकर प्रत्येक विधि के समीकरणों को हल करना समीचीन मानता हूं।
छात्र समाधान बताता है, शिक्षक टैबलेट पर लिखता है, पूरी प्रक्रिया स्क्रीन पर प्रदर्शित होती है। यह आपको अपनी मेमोरी में पहले से कवर की गई सामग्री को जल्दी और कुशलता से पुनर्स्थापित करने की अनुमति देगा।
समीकरण हल करें:
1) परिवर्तनशील परिवर्तन 6cos 2 x + 5sinx - 7 = 0
2) गुणनखंडन 3cos(x/3) + 4cos 2 (x/3) = 0
3) सजातीय समीकरण पाप 2 x + 3cos 2 x - 2sin2x = 0
4) योग को उत्पाद cos5x + cos7x = cos(π + 6x) में परिवर्तित करना
5) गुणनफल को योग 2sinx syn2x + cos3x = 0 में परिवर्तित करना
6) पाप 2x की डिग्री कम करना - पाप 2 2x + पाप 2 3x = 0.5
7) सार्वत्रिक त्रिकोणमितीय प्रतिस्थापन synx + 5cosx + 5 = 0।
इस समीकरण को हल करते समय, यह ध्यान दिया जाना चाहिए कि इस पद्धति के उपयोग से परिभाषा का क्षेत्र संकुचित हो जाता है, क्योंकि साइन और कोसाइन को tg(x/2) द्वारा प्रतिस्थापित किया जाता है। इसलिए, उत्तर लिखने से पहले, यह जांचना आवश्यक है कि सेट π + 2πn, n Z से संख्याएँ इस समीकरण के घोड़े हैं या नहीं।
8) एक सहायक कोण का परिचय √3sinx + cosx - √2 = 0
9) किसी त्रिकोणमितीय फलन cosx cos2x cos4x = 1/8 से गुणा।
5. त्रिकोणमितीय समीकरणों के मूलों का चयन (20 मिनट)
चूंकि विश्वविद्यालयों में प्रवेश करते समय भयंकर प्रतिस्पर्धा की स्थिति में, परीक्षा के पहले भाग का समाधान पर्याप्त नहीं होता है, अधिकांश छात्रों को दूसरे भाग (सी1, सी2, सी3) के कार्यों पर ध्यान देना चाहिए।
इसलिए, पाठ के इस चरण का उद्देश्य पहले अध्ययन की गई सामग्री को याद करना, 2011 में यूएसई से समस्या सी1 को हल करने के लिए तैयार करना है।
ऐसे त्रिकोणमितीय समीकरण हैं जिनमें उत्तर लिखते समय आपको मूलों का चयन करना होगा। यह कुछ प्रतिबंधों के कारण है, उदाहरण के लिए: भिन्न का हर शून्य के बराबर नहीं है, सम डिग्री के मूल के अंतर्गत अभिव्यक्ति गैर-नकारात्मक है, लघुगणक के चिह्न के अंतर्गत अभिव्यक्ति सकारात्मक है, आदि।
ऐसे समीकरणों को बढ़ी हुई जटिलता के समीकरण माना जाता है और यूएसई संस्करण में वे दूसरे भाग, अर्थात् सी1 में हैं।
प्रश्न हल करें:
यदि तब अंश शून्य है ![]() यूनिट सर्कल का उपयोग करके, हम जड़ों का चयन करेंगे (चित्र 1 देखें)
यूनिट सर्कल का उपयोग करके, हम जड़ों का चयन करेंगे (चित्र 1 देखें)

चित्र 1।
हमें x = π + 2πn, n Z मिलता है
उत्तर: π + 2πn, n Z
स्क्रीन पर, जड़ों का चयन एक रंगीन छवि में एक वृत्त पर दिखाया गया है।
उत्पाद शून्य के बराबर होता है जब कम से कम एक कारक शून्य के बराबर होता है, और चाप, एक ही समय में, अपना अर्थ नहीं खोता है। तब

यूनिट सर्कल का उपयोग करके, जड़ों का चयन करें (चित्र 2 देखें)

अनुभाग: अंक शास्त्र
कक्षा: 11
पाठ 1
विषय: ग्रेड 11 (परीक्षा की तैयारी)
त्रिकोणमितीय व्यंजकों का सरलीकरण.
सरलतम त्रिकोणमितीय समीकरणों का समाधान. (2 घंटे)
लक्ष्य:
- त्रिकोणमिति सूत्रों के उपयोग और सरलतम त्रिकोणमितीय समीकरणों के समाधान से संबंधित छात्रों के ज्ञान और कौशल को व्यवस्थित, सामान्यीकृत, विस्तारित करें।
पाठ के लिए उपकरण:
पाठ संरचना:
- ऑर्गमोमेंट
- लैपटॉप पर परीक्षण. नतीजों की चर्चा.
- त्रिकोणमितीय व्यंजकों को सरल बनाना
- सरलतम त्रिकोणमितीय समीकरणों का समाधान
- स्वतंत्र काम।
- पाठ का सारांश. गृहकार्य की व्याख्या.
1. आयोजन का क्षण. (दो मिनट।)
शिक्षक दर्शकों का स्वागत करता है, पाठ के विषय की घोषणा करता है, याद दिलाता है कि पहले त्रिकोणमिति सूत्रों को दोहराने का कार्य दिया गया था और छात्रों को परीक्षण के लिए तैयार किया गया था।
2. परीक्षण. (15 मिनट + 3 मिनट की चर्चा)
लक्ष्य त्रिकोणमितीय सूत्रों के ज्ञान और उन्हें लागू करने की क्षमता का परीक्षण करना है। प्रत्येक छात्र के डेस्क पर एक लैपटॉप होता है जिसमें परीक्षण का विकल्प होता है।
कई विकल्प हो सकते हैं, मैं उनमें से एक का उदाहरण दूंगा:
मैं विकल्प.
भावों को सरल बनाएं:
ए) बुनियादी त्रिकोणमितीय पहचान
1. पाप 2 3y + cos 2 3y + 1;
बी) अतिरिक्त सूत्र
3. पाप5x - पाप3x;
ग) किसी उत्पाद को योग में परिवर्तित करना
6. 2sin8y cos3y;
घ) द्विकोण सूत्र
7.2sin5x cos5x;
ई) अर्धकोण सूत्र
च) त्रिकोण सूत्र
छ) सार्वभौमिक प्रतिस्थापन
ज) डिग्री कम करना
16. कॉस 2 (3x/7);
प्रत्येक फार्मूले के सामने छात्र लैपटॉप पर अपना उत्तर देखते हैं।
कार्य की जाँच कम्प्यूटर द्वारा तुरन्त की जाती है। परिणाम सभी के देखने के लिए बड़ी स्क्रीन पर प्रदर्शित किए जाते हैं।
साथ ही, काम खत्म होने के बाद सही उत्तर छात्रों के लैपटॉप पर दिखाए जाते हैं। प्रत्येक छात्र यह देखता है कि गलती कहां हुई है और उसे कौन से फॉर्मूले दोहराने की जरूरत है।
3. त्रिकोणमितीय व्यंजकों का सरलीकरण। (25 मि.)
लक्ष्य त्रिकोणमिति के बुनियादी सूत्रों के अनुप्रयोग को दोहराना, काम करना और समेकित करना है। परीक्षा से समस्या B7 का समाधान।
इस स्तर पर, कक्षा को मजबूत (बाद में सत्यापन के साथ स्वतंत्र रूप से काम करें) और शिक्षक के साथ काम करने वाले कमजोर छात्रों के समूहों में विभाजित करने की सलाह दी जाती है।
मजबूत छात्रों के लिए असाइनमेंट (मुद्रित आधार पर पहले से तैयार)। USE 2011 के अनुसार, मुख्य जोर कटौती और दोहरे कोण फ़ार्मुलों पर है।
अभिव्यक्ति को सरल बनाएं (मजबूत शिक्षार्थियों के लिए):

समानांतर में, शिक्षक कमजोर छात्रों के साथ काम करता है, छात्रों के निर्देशन में स्क्रीन पर कार्यों पर चर्चा करता है और उन्हें हल करता है।
गणना करें:
5) पाप(270º - α) + cos(270º + α)
6) 
सरल बनाएं:

अब बारी थी सशक्त समूह के कार्य के परिणामों पर चर्चा की।
उत्तर स्क्रीन पर दिखाई देते हैं, और साथ ही, एक वीडियो कैमरे की मदद से, 5 अलग-अलग छात्रों का काम प्रदर्शित होता है (प्रत्येक के लिए एक कार्य)।
निर्बल समूह परिस्थिति एवं समाधान विधि को देखता है। चर्चा और विश्लेषण होता है. तकनीकी साधनों के प्रयोग से यह शीघ्रता से होता है।
4. सरलतम त्रिकोणमितीय समीकरणों का समाधान। (30 मिनट।)
लक्ष्य सरलतम त्रिकोणमितीय समीकरणों के समाधान को दोहराना, व्यवस्थित करना और सामान्यीकृत करना, उनकी जड़ों को रिकॉर्ड करना है। समस्या B3 का समाधान.
कोई भी त्रिकोणमितीय समीकरण, चाहे हम उसे कैसे भी हल करें, सबसे सरल की ओर ले जाता है।
कार्य पूरा करते समय, छात्रों को विशेष मामलों के समीकरणों की जड़ों को सामान्य रूप में लिखने और अंतिम समीकरण में जड़ों के चयन पर ध्यान देना चाहिए।
समीकरण हल करें:

उत्तर का सबसे छोटा सकारात्मक मूल लिखिए।
5. स्वतंत्र कार्य (10 मिनट)
लक्ष्य अर्जित कौशल का परीक्षण करना, समस्याओं, त्रुटियों की पहचान करना और उन्हें खत्म करने के तरीकों की पहचान करना है।
छात्र की पसंद पर विभिन्न प्रकार के काम की पेशकश की जाती है।
"3" के लिए विकल्प
1) व्यंजक का मान ज्ञात कीजिए ![]()
2) अभिव्यक्ति 1 - पाप 2 3α - कॉस 2 3α को सरल बनाएं
3) समीकरण हल करें ![]()
"4" के लिए विकल्प
1) व्यंजक का मान ज्ञात कीजिए
2) समीकरण हल करें ![]() अपने उत्तर का सबसे छोटा सकारात्मक मूल लिखिए।
अपने उत्तर का सबसे छोटा सकारात्मक मूल लिखिए।
"5" के लिए विकल्प
1) यदि tgα ज्ञात करें ![]()
2) समीकरण का मूल ज्ञात कीजिए ![]() अपने उत्तर का सबसे छोटा सकारात्मक मूल लिखिए।
अपने उत्तर का सबसे छोटा सकारात्मक मूल लिखिए।
6. पाठ का सारांश (5 मिनट)
शिक्षक ने इस तथ्य का सारांश दिया कि पाठ में त्रिकोणमितीय सूत्रों को दोहराया और समेकित किया गया, सबसे सरल त्रिकोणमितीय समीकरणों का समाधान।
अगले पाठ में मौके की जांच के साथ गृहकार्य (पहले से मुद्रित आधार पर तैयार) सौंपा जाता है।
समीकरण हल करें:

9) ![]()
10) ![]() अपना उत्तर सबसे छोटे सकारात्मक मूल के रूप में दें।
अपना उत्तर सबसे छोटे सकारात्मक मूल के रूप में दें।
पाठ 2
विषय: ग्रेड 11 (परीक्षा की तैयारी)
त्रिकोणमितीय समीकरणों को हल करने की विधियाँ। जड़ चयन. (2 घंटे)
लक्ष्य:
- विभिन्न प्रकार के त्रिकोणमितीय समीकरणों को हल करने पर ज्ञान को सामान्य बनाना और व्यवस्थित करना।
- छात्रों की गणितीय सोच, निरीक्षण करने, तुलना करने, सामान्यीकरण करने, वर्गीकृत करने की क्षमता के विकास को बढ़ावा देना।
- छात्रों को मानसिक गतिविधि की प्रक्रिया में कठिनाइयों को दूर करने, आत्म-नियंत्रण, अपनी गतिविधियों का आत्मनिरीक्षण करने के लिए प्रोत्साहित करें।
पाठ के लिए उपकरण:केआरएमयू, प्रत्येक छात्र के लिए लैपटॉप।
पाठ संरचना:
- ऑर्गमोमेंट
- चर्चा डी/एस एवं समोट। अंतिम पाठ का कार्य
- त्रिकोणमितीय समीकरणों को हल करने की विधियों की पुनरावृत्ति।
- त्रिकोणमितीय समीकरणों को हल करना
- त्रिकोणमितीय समीकरणों में मूलों का चयन.
- स्वतंत्र काम।
- पाठ का सारांश. गृहकार्य।
1. आयोजन का क्षण (2 मिनट)
शिक्षक दर्शकों का स्वागत करता है, पाठ के विषय और कार्य योजना की घोषणा करता है।
2.ए) होमवर्क का विश्लेषण (5 मिनट)
लक्ष्य प्रदर्शन की जाँच करना है. वीडियो कैमरे की सहायता से एक कार्य को स्क्रीन पर प्रदर्शित किया जाता है, बाकी को शिक्षक द्वारा जांचने के लिए चुनिंदा रूप से एकत्र किया जाता है।
बी) स्वतंत्र कार्य का विश्लेषण (3 मिनट)
लक्ष्य गलतियों को सुलझाना, उन्हें दूर करने के उपाय बताना है।
स्क्रीन पर उत्तर और समाधान हैं, छात्रों ने अपना काम पहले ही जारी कर दिया है। विश्लेषण तेजी से चल रहा है.
3. त्रिकोणमितीय समीकरणों को हल करने की विधियों की पुनरावृत्ति (5 मिनट)
लक्ष्य त्रिकोणमितीय समीकरणों को हल करने के तरीकों को याद करना है।
विद्यार्थियों से पूछें कि वे त्रिकोणमितीय समीकरणों को हल करने की कौन सी विधियाँ जानते हैं। इस बात पर ज़ोर दें कि तथाकथित बुनियादी (अक्सर उपयोग की जाने वाली) विधियाँ हैं:
- परिवर्तनीय प्रतिस्थापन,
- गुणनखंडन,
- सजातीय समीकरण,
और लागू तरीके हैं:
- किसी राशि को उत्पाद में और उत्पाद को राशि में बदलने के फ़ार्मुलों के अनुसार,
- कमी सूत्रों द्वारा,
- सार्वभौमिक त्रिकोणमितीय प्रतिस्थापन
- एक सहायक कोण का परिचय,
- किसी त्रिकोणमितीय फलन द्वारा गुणन।
यह भी याद रखना चाहिए कि एक समीकरण को विभिन्न तरीकों से हल किया जा सकता है।
4. त्रिकोणमितीय समीकरण हल करना (30 मिनट)
लक्ष्य इस विषय पर ज्ञान और कौशल को सामान्य बनाना और समेकित करना है, ताकि यूएसई से सी1 को हल करने की तैयारी की जा सके।
मैं छात्रों के साथ मिलकर प्रत्येक विधि के समीकरणों को हल करना समीचीन मानता हूं।
छात्र समाधान बताता है, शिक्षक टैबलेट पर लिखता है, पूरी प्रक्रिया स्क्रीन पर प्रदर्शित होती है। यह आपको अपनी मेमोरी में पहले से कवर की गई सामग्री को जल्दी और कुशलता से पुनर्स्थापित करने की अनुमति देगा।
समीकरण हल करें:
1) परिवर्तनशील परिवर्तन 6cos 2 x + 5sinx - 7 = 0
2) गुणनखंडन 3cos(x/3) + 4cos 2 (x/3) = 0
3) सजातीय समीकरण पाप 2 x + 3cos 2 x - 2sin2x = 0
4) योग को उत्पाद cos5x + cos7x = cos(π + 6x) में परिवर्तित करना
5) गुणनफल को योग 2sinx syn2x + cos3x = 0 में परिवर्तित करना
6) पाप 2x की डिग्री कम करना - पाप 2 2x + पाप 2 3x = 0.5
7) सार्वत्रिक त्रिकोणमितीय प्रतिस्थापन synx + 5cosx + 5 = 0।
इस समीकरण को हल करते समय, यह ध्यान दिया जाना चाहिए कि इस पद्धति के उपयोग से परिभाषा का क्षेत्र संकुचित हो जाता है, क्योंकि साइन और कोसाइन को tg(x/2) द्वारा प्रतिस्थापित किया जाता है। इसलिए, उत्तर लिखने से पहले, यह जांचना आवश्यक है कि सेट π + 2πn, n Z से संख्याएँ इस समीकरण के घोड़े हैं या नहीं।
8) एक सहायक कोण का परिचय √3sinx + cosx - √2 = 0
9) किसी त्रिकोणमितीय फलन cosx cos2x cos4x = 1/8 से गुणा।
5. त्रिकोणमितीय समीकरणों के मूलों का चयन (20 मिनट)
चूंकि विश्वविद्यालयों में प्रवेश करते समय भयंकर प्रतिस्पर्धा की स्थिति में, परीक्षा के पहले भाग का समाधान पर्याप्त नहीं होता है, अधिकांश छात्रों को दूसरे भाग (सी1, सी2, सी3) के कार्यों पर ध्यान देना चाहिए।
इसलिए, पाठ के इस चरण का उद्देश्य पहले अध्ययन की गई सामग्री को याद करना, 2011 में यूएसई से समस्या सी1 को हल करने के लिए तैयार करना है।
ऐसे त्रिकोणमितीय समीकरण हैं जिनमें उत्तर लिखते समय आपको मूलों का चयन करना होगा। यह कुछ प्रतिबंधों के कारण है, उदाहरण के लिए: भिन्न का हर शून्य के बराबर नहीं है, सम डिग्री के मूल के अंतर्गत अभिव्यक्ति गैर-नकारात्मक है, लघुगणक के चिह्न के अंतर्गत अभिव्यक्ति सकारात्मक है, आदि।
ऐसे समीकरणों को बढ़ी हुई जटिलता के समीकरण माना जाता है और यूएसई संस्करण में वे दूसरे भाग, अर्थात् सी1 में हैं।
प्रश्न हल करें:
यदि तब अंश शून्य है ![]() यूनिट सर्कल का उपयोग करके, हम जड़ों का चयन करेंगे (चित्र 1 देखें)
यूनिट सर्कल का उपयोग करके, हम जड़ों का चयन करेंगे (चित्र 1 देखें)

चित्र 1।
हमें x = π + 2πn, n Z मिलता है
उत्तर: π + 2πn, n Z
स्क्रीन पर, जड़ों का चयन एक रंगीन छवि में एक वृत्त पर दिखाया गया है।
उत्पाद शून्य के बराबर होता है जब कम से कम एक कारक शून्य के बराबर होता है, और चाप, एक ही समय में, अपना अर्थ नहीं खोता है। तब

यूनिट सर्कल का उपयोग करके, जड़ों का चयन करें (चित्र 2 देखें)

चित्र 2।
5) ![]()
आइए सिस्टम पर चलते हैं:
![]()
सिस्टम के पहले समीकरण में, हम परिवर्तन लॉग 2 (sinx) = y बनाते हैं, फिर हम समीकरण प्राप्त करते हैं ![]() , सिस्टम पर वापस
, सिस्टम पर वापस
यूनिट सर्कल का उपयोग करके, हम जड़ों का चयन करते हैं (चित्र 5 देखें),

चित्र 5

6. स्वतंत्र कार्य (15 मिनट)
लक्ष्य सामग्री को समेकित करना और आत्मसात करने की जांच करना, त्रुटियों की पहचान करना और उन्हें ठीक करने के तरीकों की रूपरेखा तैयार करना है।
कार्य तीन संस्करणों में प्रस्तुत किया जाता है, जो छात्रों की पसंद पर मुद्रित आधार पर पहले से तैयार किया जाता है।
समीकरणों को किसी भी तरह से हल किया जा सकता है.
"3" के लिए विकल्प
समीकरण हल करें:
1) 2sin 2 x + synx - 1 = 0
2) पाप2x = √3cosx
"4" के लिए विकल्प
समीकरण हल करें:
1)cos2x = 11sinx - 5
2) (2sinx + √3)log 8 (cosx) = 0
"5" के लिए विकल्प
समीकरण हल करें:
1) 2sinx - 3cosx = 2
2) ![]()
7. पाठ का सारांश, गृहकार्य (5 मिनट)
शिक्षक पाठ का सारांश देते हुए एक बार फिर इस तथ्य की ओर ध्यान आकर्षित करते हैं कि त्रिकोणमितीय समीकरण को कई तरीकों से हल किया जा सकता है। त्वरित परिणाम प्राप्त करने का सबसे अच्छा तरीका वह है जो किसी विशेष छात्र द्वारा सबसे अच्छा सीखा जाता है।
परीक्षा की तैयारी करते समय, आपको समीकरणों को हल करने के लिए सूत्रों और विधियों को व्यवस्थित रूप से दोहराना होगा।
होमवर्क (मुद्रित आधार पर पहले से तैयार) वितरित किया जाता है और कुछ समीकरणों को हल करने के तरीकों पर टिप्पणी की जाती है।
समीकरण हल करें:
1) cosx + cos5x = cos3x + cos7x
2) 5sin(x/6) - cos(x/3) + 3 = 0
3) 4sin 2x + syn2x = 3
4) पाप 2 x + पाप 2 2x - पाप 2 3x - पाप 2 4x = 0
5) cos3x cos6x = cos4x cos7x
6) 4sinx - 6cosx = 1
7) 3sin2x + 4 cos2x = 5
8) cosx cos2x cos4x cos8x = (1/8) cos15x
9) (2sin 2 x - synx)log 3 (2cos 2 x + cosx) = 0
10) (2cos 2 x - √3cosx)log 7 (-tgx) = 0
11) ![]()
में समान परिवर्तन त्रिकोणमितीय अभिव्यक्तियाँनिम्नलिखित बीजीय युक्तियों का उपयोग किया जा सकता है: समान पदों को जोड़ना और घटाना; सामान्य गुणनखंड को कोष्ठक से बाहर निकालना; समान मान से गुणा और भाग; संक्षिप्त गुणन सूत्रों का अनुप्रयोग; पूर्ण वर्ग का चयन; एक वर्ग त्रिपद का गुणनखंडन; परिवर्तनों को सरल बनाने के लिए नए चरों का परिचय।
भिन्नों वाले त्रिकोणमितीय व्यंजकों को परिवर्तित करते समय, आप अनुपात, भिन्नों में कमी, या भिन्नों को एक सामान्य हर में घटाने के गुणों का उपयोग कर सकते हैं। इसके अलावा, आप भिन्न के पूर्णांक भाग के चयन का उपयोग कर सकते हैं, अंश के अंश और हर को समान मान से गुणा कर सकते हैं, और यदि संभव हो तो अंश या हर की एकरूपता को भी ध्यान में रख सकते हैं। यदि आवश्यक हो, तो आप भिन्न को कई सरल भिन्नों के योग या अंतर के रूप में निरूपित कर सकते हैं।
इसके अलावा, त्रिकोणमितीय अभिव्यक्तियों को परिवर्तित करने के लिए सभी आवश्यक तरीकों को लागू करते समय, परिवर्तित अभिव्यक्तियों के अनुमेय मूल्यों की सीमा को लगातार ध्यान में रखना आवश्यक है।
आइए कुछ उदाहरण देखें.
उदाहरण 1
A = (sin (2x - π) cos (3π - x) + syn (2x - 9π/2) cos (x + π/2)) 2 + (cos (x - π/2) cos ( 2x - 7π) की गणना करें /2)+
+
पाप (3π/2 - x) पाप (2x -5π/2)) 2
समाधान।
यह कमी सूत्रों से निम्नानुसार है:
पाप (2x - π) = -sin 2x; cos (3π - x) = -cos x;
पाप (2x - 9π / 2) \u003d -cos 2x; cos (x + π/2) = -sin x;
cos (x - π / 2) = पाप x; cos (2x - 7π/2) = -sin 2x;
पाप (3π / 2 - x) = -cos x; पाप (2x - 5π / 2) \u003d -cos 2x।
जहां से, तर्कों को जोड़ने के सूत्रों और मूल त्रिकोणमितीय पहचान के आधार पर, हम प्राप्त करते हैं
ए \u003d (sin 2x cos x + cos 2x पाप x) 2 + (-sin x पाप 2x + cos x cos 2x) 2 \u003d पाप 2 (2x + x) + cos 2 (x + 2x) \u003d
= पाप 2 3x + cos 2 3x = 1
उत्तर 1।
उदाहरण 2
अभिव्यक्ति M = cos α + cos (α + β) cos γ + cos β – syn (α + β) syn γ + cos γ को एक गुणनफल में बदलें।
समाधान।
उचित समूहीकरण के बाद, तर्कों को जोड़ने के सूत्रों और त्रिकोणमितीय कार्यों के योग को उत्पाद में परिवर्तित करने के सूत्रों से, हमारे पास है
М = (cos (α + β) cos γ - पाप (α + β) पाप γ) + cos α + (cos β + cos γ) =
2cos ((β + γ)/2) cos ((β – γ)/2) + (cos α + cos (α + β + γ)) =
2cos ((β + γ)/2) cos ((β – γ)/2) + 2cos (α + (β + γ)/2) cos ((β + γ)/2)) =
2cos ((β + γ)/2) (cos ((β – γ)/2) + cos (α + (β + γ)/2)) =
2cos ((β + γ)/2) 2cos ((β – γ)/2 + α + (β + γ)/2)/2) cos ((β – γ)/2) – (α + ( β + γ)/2)/2) =
4cos ((β + γ)/2) cos ((α + β)/2) cos ((α + γ)/2)।
उत्तर: М = 4cos ((α + β)/2) cos ((α + γ)/2) cos ((β + γ)/2)।
उदाहरण 3.
दिखाएँ कि अभिव्यक्ति A \u003d cos 2 (x + π / 6) - cos (x + π / 6) cos (x - π / 6) + cos 2 (x - π / 6) R से सभी x के लिए लेता है। और वही मूल्य. यह मान ज्ञात कीजिए।
समाधान।
हम इस समस्या को हल करने के लिए दो तरीके प्रस्तुत करते हैं। पहली विधि को लागू करते हुए, पूर्ण वर्ग को अलग करके और संबंधित बुनियादी त्रिकोणमितीय सूत्रों का उपयोग करके, हम प्राप्त करते हैं
ए \u003d (cos (x + π / 6) - cos (x - π / 6)) 2 + cos (x - π / 6) cos (x - π / 6) \u003d
4sin 2 x पाप 2 π/6 + 1/2(cos 2x + cos π/3) =
पाप 2 x + 1/2 cos 2x + 1/4 = 1/2 (1 - cos 2x) + 1/2 cos 2x + 1/4 = 3/4।
समस्या को दूसरे तरीके से हल करते हुए, A को R से x का एक फलन मानें और इसके व्युत्पन्न की गणना करें। परिवर्तनों के बाद, हम पाते हैं
А´ = -2cos (x + π/6) पाप (x + π/6) + (sin (x + π/6) cos (x - π/6) + cos (x + π/6) पाप ( x + π/6)) - 2cos (x - π/6) पाप (x - π/6) =
पाप 2(x + π/6) + पाप ((x + π/6) + (x - π/6)) - पाप 2(x - π/6) =
पाप 2x - (पाप (2x + π/3) + पाप (2x - π/3)) =
पाप 2x - 2 पाप 2x क्योंकि π/3 = पाप 2x - पाप 2x ≡ 0.
इसलिए, किसी अंतराल पर अवकलनीय फलन की स्थिरता की कसौटी के आधार पर, हम यह निष्कर्ष निकालते हैं
A(x) ≡ (0) = cos 2 π/6 - cos 2 π/6 + cos 2 π/6 = (√3/2) 2 = 3/4, x ∈ R. 
उत्तर: A = 3/4 x € R के लिए।
त्रिकोणमितीय सर्वसमिकाओं को सिद्ध करने की मुख्य विधियाँ हैं:
ए)उपयुक्त परिवर्तनों द्वारा पहचान के बाएँ पक्ष को दाएँ पक्ष में कम करना;
बी)पहचान के दाहिने हिस्से को बाईं ओर कम करना;
वी)पहचान के दाएं और बाएं हिस्सों को एक ही रूप में कम करना;
जी)पहचान सिद्ध होने के बाएँ और दाएँ भागों के बीच का अंतर शून्य हो जाना।
उदाहरण 4
जांचें कि cos 3x = -4cos x cos (x + π/3) cos (x + 2π/3)।
समाधान।
इस पहचान के दाहिने हिस्से को संबंधित त्रिकोणमितीय सूत्रों के अनुसार बदलना, हमारे पास है
4cos x cos (x + π/3) cos (x + 2π/3) =
2cos x (cos ((x + π/3) + (x + 2π/3)) + cos ((x + π/3) – (x + 2π/3))) =
2cos x (cos (2x + π) + cos π/3) =
2cos x cos 2x - cos x = (cos 3x + cos x) - cos x = cos 3x।
पहचान का दाहिना भाग बाईं ओर कम हो जाता है।
उदाहरण 5
साबित करें कि पाप 2 α + पाप 2 β + पाप 2 γ - 2cos α cos β cos γ = 2 यदि α, β, γ किसी त्रिभुज के आंतरिक कोण हैं।
समाधान।
इस बात को ध्यान में रखते हुए कि α, β, γ किसी त्रिभुज के आंतरिक कोण हैं, हम इसे प्राप्त करते हैं
α + β + γ = π और इसलिए γ = π – α – β.
पाप 2 α + पाप 2 β + पाप 2 γ - 2cos α cos β cos γ =
पाप 2 α + पाप 2 β + पाप 2 (π - α - β) - 2cos α cos β cos (π - α - β) =
पाप 2 α + पाप 2 β + पाप 2 (α + β) + (cos (α + β) + cos (α - β) (cos (α + β) =
पाप 2 α + पाप 2 β + (पाप 2 (α + β) + cos 2 (α + β)) + cos (α - β) (cos (α + β) =
1/2 (1 - cos 2α) + ½ (1 - cos 2β) + 1 + 1/2 (cos 2α + cos 2β) = 2.
मूल समानता सिद्ध होती है।
उदाहरण 6
साबित करें कि त्रिभुज के कोण α, β, γ में से किसी एक के लिए 60° के बराबर होने के लिए, यह आवश्यक और पर्याप्त है कि पाप 3α + पाप 3β + पाप 3γ = 0.
समाधान।
इस समस्या की स्थिति आवश्यकता और पर्याप्तता दोनों के प्रमाण को मानती है।
पहले हम साबित करते हैं ज़रूरत.
ऐसा दिखाया जा सकता है
पाप 3α + पाप 3β + पाप 3γ = -4cos (3α/2) cos (3β/2) cos (3γ/2)।
इसलिए, यह ध्यान में रखते हुए कि cos (3/2 60°) = cos 90° = 0, हम पाते हैं कि यदि कोण α, β या γ में से एक 60° के बराबर है, तो
cos (3α/2) cos (3β/2) cos (3γ/2) = 0 और इसलिए पाप 3α + पाप 3β + पाप 3γ = 0।
चलिए अब साबित करते हैं पर्याप्ततानिर्दिष्ट शर्त.
यदि पाप 3α + पाप 3β + पाप 3γ = 0, तो cos (3α/2) cos (3β/2) cos (3γ/2) = 0, और इसलिए
या तो cos (3α/2) = 0, या cos (3β/2) = 0, या cos (3γ/2) = 0।
इस तरह,
या 3α/2 = π/2 + πk, अर्थात α = π/3 + 2πk/3, 
या 3β/2 = π/2 + πk, अर्थात β = π/3 + 2πk/3,
या 3γ/2 = π/2 + πk,
वे। γ = π/3 + 2πk/3, जहां k ϵ Z.
इस तथ्य से कि α, β, γ एक त्रिभुज के कोण हैं, हमारे पास है
0 < α < π, 0 < β < π, 0 < γ < π.
इसलिए, α = π/3 + 2πk/3 या β = π/3 + 2πk/3 या के लिए
γ = π/3 + 2πk/3 सभी kϵZ में से केवल k = 0 फिट बैठता है।
इससे यह निष्कर्ष निकलता है कि या तो α = π/3 = 60°, या β = π/3 = 60°, या γ = π/3 = 60°।
दावा सिद्ध हो गया है.
क्या आपका कोई प्रश्न है? क्या आप नहीं जानते कि त्रिकोणमितीय व्यंजकों को सरल कैसे बनाया जाए?
ट्यूटर की सहायता पाने के लिए - रजिस्टर करें।
पहला पाठ निःशुल्क है!
साइट, सामग्री की पूर्ण या आंशिक प्रतिलिपि के साथ, स्रोत के लिए एक लिंक आवश्यक है।



