गेंद की परिभाषा. अंक शास्त्र

एक गेंद एक पिंड है जिसमें अंतरिक्ष के सभी बिंदु शामिल होते हैं जो किसी दिए गए बिंदु से अधिक दूरी पर स्थित नहीं होते हैं। इस बिंदु को गेंद का केंद्र कहा जाता है, और इस दूरी को गेंद की त्रिज्या कहा जाता है। गेंद की सीमा को गोलाकार सतह या गोला कहा जाता है। गोले के बिंदु गेंद के वे सभी बिंदु होते हैं जिन्हें केंद्र से त्रिज्या के बराबर दूरी पर हटाया जाता है। कोई भी खंड जो गेंद के केंद्र को गोलाकार सतह पर एक बिंदु से जोड़ता है उसे त्रिज्या भी कहा जाता है। गेंद के केंद्र से गुजरने वाला और गोलाकार सतह पर दो बिंदुओं को जोड़ने वाला खंड व्यास कहलाता है। किसी भी व्यास के सिरे को गेंद के व्यास के विपरीत बिंदु कहा जाता है।

एक गेंद एक शंकु और एक सिलेंडर की तरह परिक्रमण का एक पिंड है। एक गेंद को उसके व्यास के चारों ओर एक अक्ष के रूप में अर्धवृत्त घुमाकर प्राप्त किया जाता है।

गेंद का सतह क्षेत्र सूत्रों का उपयोग करके पाया जा सकता है:

जहाँ r गेंद की त्रिज्या है, d गेंद का व्यास है।

गेंद का आयतन सूत्र द्वारा ज्ञात किया जाता है:

वी = 4 / 3 πr 3,

जहाँ r गेंद की त्रिज्या है।

प्रमेय. एक समतल द्वारा गेंद का प्रत्येक भाग एक वृत्त है। इस वृत्त का केंद्र गेंद के केंद्र से काटने वाले तल पर खींचे गए लंबवत का आधार है।

इस प्रमेय के आधार पर, यदि केंद्र O और त्रिज्या R वाली एक गेंद को विमान α द्वारा प्रतिच्छेद किया जाता है, तो क्रॉस-सेक्शन के परिणामस्वरूप केंद्र K के साथ त्रिज्या r का एक वृत्त बनता है। विमान द्वारा गेंद के अनुभाग की त्रिज्या हो सकती है सूत्र द्वारा पाया गया

सूत्र से यह स्पष्ट है कि केंद्र से समदूरस्थ तल गेंद को समान वृत्तों में काटते हैं। अनुभाग की त्रिज्या जितनी अधिक होगी, काटने वाला विमान गेंद के केंद्र के जितना करीब होगा, यानी दूरी उतनी ही कम होगी। सबसे बड़ी त्रिज्या में गेंद के केंद्र से गुजरने वाले विमान का एक खंड होता है। इस वृत्त की त्रिज्या गेंद की त्रिज्या के बराबर होती है।

गेंद के केंद्र से गुजरने वाले तल को केंद्रीय तल कहा जाता है। व्यासीय तल द्वारा गेंद के खंड को एक महान वृत्त कहा जाता है, और एक गोले के खंड को एक महान वृत्त कहा जाता है, और एक गोले के खंड को एक महान वृत्त कहा जाता है।

प्रमेय. किसी गेंद का कोई भी व्यासीय तल उसका सममिति तल होता है। गेंद का केंद्र इसकी समरूपता का केंद्र है।

वह तल जो गोलाकार सतह के बिंदु A से होकर गुजरता है और बिंदु A पर खींची गई त्रिज्या के लंबवत है, स्पर्शरेखा तल कहलाता है। बिंदु A को स्पर्शरेखा बिंदु कहा जाता है.

प्रमेय. स्पर्शरेखा तल में गेंद के साथ केवल एक ही उभयनिष्ठ बिंदु होता है - संपर्क बिंदु।

इस बिंदु पर खींची गई त्रिज्या के लंबवत गोलाकार सतह के बिंदु A से होकर गुजरने वाली सीधी रेखा को स्पर्शरेखा कहा जाता है।

प्रमेय. गोलाकार सतह पर किसी भी बिंदु से अनंत संख्या में स्पर्शरेखाएँ गुजरती हैं, और वे सभी गेंद के स्पर्शरेखा तल में स्थित होती हैं।

गोलाकार खंड एक गेंद का वह भाग होता है जो एक समतल द्वारा काटा जाता है। वृत्त ABC गोलाकार खंड का आधार है। वृत्त एबीसी के केंद्र एन से गोलाकार सतह के साथ चौराहे तक खींचा गया लंबवत खंड एमएन गोलाकार खंड की ऊंचाई है। बिंदु M गोलाकार खंड का शीर्ष है।

एक गोलाकार खंड के सतह क्षेत्र की गणना सूत्र का उपयोग करके की जा सकती है:

एक गोलाकार खंड का आयतन सूत्र का उपयोग करके पाया जा सकता है:

वी = πएच 2 (आर - 1/3एच),

जहाँ R बड़े वृत्त की त्रिज्या है, h गोलाकार खंड की ऊँचाई है।

एक गोलाकार खंड और एक शंकु से एक गोलाकार क्षेत्र इस प्रकार प्राप्त होता है। यदि गोलाकार खंड गोलार्ध से छोटा है, तो गोलाकार खंड एक शंकु से पूरक होता है, जिसका शीर्ष गेंद के केंद्र में होता है, और आधार खंड का आधार होता है। यदि खंड गोलार्ध से बड़ा है, तो निर्दिष्ट शंकु को इससे हटा दिया जाता है।

एक गोलाकार क्षेत्र एक गोलाकार खंड की घुमावदार सतह (हमारे चित्र में, यह AMCB है) और एक शंक्वाकार सतह (हमारे चित्र में, यह OABC है) से घिरी हुई गेंद का एक हिस्सा है, जिसका आधार आधार है खंड (एबीसी), और शीर्ष गेंद ओ का केंद्र है।

गोलाकार क्षेत्र का आयतन सूत्र द्वारा ज्ञात किया जाता है:

वी = 2/3 πआर 2 एच.

गोलाकार परत गोलाकार सतह को प्रतिच्छेद करने वाले दो समानांतर विमानों (आकृति में एबीसी और डीईएफ) के बीच घिरी हुई गेंद का एक हिस्सा है। गोलाकार परत की घुमावदार सतह को गोलाकार बेल्ट (क्षेत्र) कहा जाता है। वृत्त ABC और DEF गोलाकार बेल्ट के आधार हैं। गोलाकार बेल्ट के आधारों के बीच की दूरी NK इसकी ऊंचाई है।

वेबसाइट, सामग्री को पूर्ण या आंशिक रूप से कॉपी करते समय, स्रोत के लिंक की आवश्यकता होती है।

एक गेंद और एक गोला, सबसे पहले, ज्यामितीय आकृतियाँ हैं, और यदि एक गेंद एक ज्यामितीय निकाय है, तो एक गोला गेंद की सतह है। ये आंकड़े ईसा पूर्व हजारों साल पहले दिलचस्प थे।

इसके बाद, जब यह पता चला कि पृथ्वी एक गेंद है और आकाश एक खगोलीय गोला है, तो ज्यामिति में एक नई आकर्षक दिशा विकसित हुई - एक गोले पर ज्यामिति या गोलाकार ज्यामिति। किसी गेंद के आकार और आयतन के बारे में बात करने के लिए, आपको पहले इसे परिभाषित करना होगा।

गेंद

ज्यामिति में बिंदु O पर केंद्र के साथ त्रिज्या R की एक गेंद एक ऐसा पिंड है जो अंतरिक्ष में सभी बिंदुओं द्वारा बनाई गई है जिसमें एक सामान्य संपत्ति है। ये बिंदु गेंद की त्रिज्या से अधिक दूरी पर स्थित नहीं होते हैं, अर्थात, वे गेंद के केंद्र से सभी दिशाओं में उसकी त्रिज्या से कम दूरी पर संपूर्ण स्थान भरते हैं। यदि हम केवल उन बिंदुओं पर विचार करते हैं जो गेंद के केंद्र से समान दूरी पर हैं, तो हम इसकी सतह या गेंद के खोल पर विचार करेंगे।

मुझे गेंद कैसे मिल सकती है? हम कागज से एक वृत्त काट सकते हैं और उसे उसके ही व्यास के चारों ओर घुमाना शुरू कर सकते हैं। अर्थात् वृत्त का व्यास घूर्णन अक्ष होगा। बनी हुई आकृति एक गेंद होगी। इसलिए गेंद को परिक्रमण पिंड भी कहा जाता है। क्योंकि इसे घुमाकर एक सपाट आकृति - एक वृत्त बनाया जा सकता है।

आइए कुछ हवाई जहाज़ लें और उससे अपनी गेंद काटें। जैसे हम एक संतरे को चाकू से काटते हैं. गेंद से जो टुकड़ा हम काटते हैं उसे गोलाकार खंड कहते हैं।

प्राचीन ग्रीस में, वे न केवल एक गेंद और गोले के साथ ज्यामितीय आकृतियों के रूप में काम करना जानते थे, उदाहरण के लिए, उन्हें निर्माण में उपयोग करना, बल्कि एक गेंद के सतह क्षेत्र और एक गेंद के आयतन की गणना करना भी जानते थे।

गोला गेंद की सतह का दूसरा नाम है। गोला कोई पिण्ड नहीं है - यह परिक्रमण पिण्ड की सतह है। हालाँकि, चूंकि पृथ्वी और कई पिंडों का आकार गोलाकार है, उदाहरण के लिए पानी की एक बूंद, गोले के अंदर ज्यामितीय संबंधों का अध्ययन व्यापक हो गया है।

उदाहरण के लिए, यदि हम किसी गोले के दो बिंदुओं को एक सीधी रेखा द्वारा एक दूसरे से जोड़ते हैं, तो यह सीधी रेखा एक जीवा कहलाएगी, और यदि यह जीवा गोले के केंद्र से होकर गुजरती है, जो गेंद के केंद्र से मेल खाती है। तो जीवा गोले का व्यास कहलाएगी।

यदि हम एक सीधी रेखा खींचते हैं जो गोले को केवल एक बिंदु पर स्पर्श करती है, तो यह रेखा स्पर्शरेखा कहलाएगी। इसके अलावा, इस बिंदु पर गोले की यह स्पर्श रेखा संपर्क बिंदु पर खींचे गए गोले की त्रिज्या के लंबवत होगी।

यदि हम जीवा को गोले से एक दिशा या दूसरी दिशा में एक सीधी रेखा तक बढ़ाते हैं, तो इस जीवा को छेदक कहा जाएगा। या हम इसे अलग ढंग से कह सकते हैं - गोले के छेदक में उसकी जीवा होती है।

गेंद की मात्रा

गेंद के आयतन की गणना करने का सूत्र है:

जहाँ R गेंद की त्रिज्या है।

यदि आपको गोलाकार खंड का आयतन ज्ञात करने की आवश्यकता है, तो सूत्र का उपयोग करें:

V seg =πh 2 (R-h/3), h गोलाकार खंड की ऊंचाई है।

किसी गेंद या गोले का पृष्ठीय क्षेत्रफल

किसी गोले के क्षेत्रफल या गेंद के सतह क्षेत्र की गणना करने के लिए (वे एक ही चीज़ हैं):

जहाँ R गोले की त्रिज्या है।

आर्किमिडीज़ को गेंद और गोले का बहुत शौक था, उन्होंने अपनी कब्र पर एक चित्र छोड़ने के लिए भी कहा जिसमें एक गेंद को एक सिलेंडर में अंकित किया गया था। आर्किमिडीज़ का मानना ​​था कि एक गेंद और उसकी सतह का आयतन उस सिलेंडर के आयतन और सतह के दो-तिहाई के बराबर होता है जिसमें गेंद अंकित है।

गेंद (गोलाकार)

गोलाकार सतह. गेंद (गोलाकार)। गेंद अनुभाग: वृत्त.

आर्किमिडीज़ प्रमेय. गेंद के भाग: गोलाकार खंड,

गोलाकार परत, गोलाकार बेल्ट, गोलाकार क्षेत्र।

गोलाकार सतह - यह बिंदुओं का स्थान(वे। अनेकसभी बिंदुओं की संख्या)अंतरिक्ष में, एक बिंदु से समान दूरी पर हे , जिसे गोलाकार सतह का केंद्र कहा जाता है (चित्र.90)। RADIUSएओआई व्यासअब एक वृत्त की तरह ही निर्धारित होते हैं।

गेंद (गोलाकार) - यह एक गोलाकार सतह से घिरा हुआ पिंड।कर सकना अर्धवृत्त घुमाकर गेंद प्राप्त करें (या वृत्त ) व्यास के चारों ओर। गेंद के सभी समतल खंड हैं मंडलियां (चित्र.90 ). सबसे बड़ा वृत्त गेंद के केंद्र से गुजरने वाले एक खंड में स्थित है और इसे कहा जाता है दीर्घ वृत्ताकार. इसकी त्रिज्या गेंद की त्रिज्या के बराबर होती है। कोई भी दो बड़े वृत्त गेंद के व्यास के अनुदिश प्रतिच्छेद करते हैं (एबी, चित्र 91 ).यह व्यास बड़े वृत्तों को प्रतिच्छेद करने का व्यास भी है। एक ही व्यास के सिरों पर स्थित एक गोलाकार सतह के दो बिंदुओं के माध्यम से(ए और बी, चित्र 91 ), आप अनगिनत बड़े वृत्त बना सकते हैं। उदाहरण के लिए, पृथ्वी के ध्रुवों के माध्यम से अनंत संख्या में मेरिडियन खींचे जा सकते हैं।

गोले का आयतन उसके चारों ओर घिरे बेलन के आयतन से डेढ़ गुना कम है। (चित्र.92 ), ए गेंद की सतह उसी सिलेंडर की कुल सतह से डेढ़ गुना छोटी है ( आर्किमिडीज़ प्रमेय):

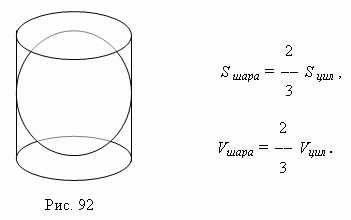
यहाँ एस गेंद और वी गेंद - क्रमशः गेंद की सतह और आयतन;

एस सिलेंडर और वी सिलेंडर - परिचालित सिलेंडर की कुल सतह और आयतन।

गेंद के भाग. गेंद का भाग (गोला) ), किसी विमान द्वारा इससे काट दिया गया (एबीसी, चित्र.93), बुलाया गेंद(गोलाकार ) खंड. सर्कल एबीसी बुलाया आधारगेंद खंड. रेखा खंडएम.एन. केंद्र से खींचा गया लंबएन सर्कल एबीसी जब तक यह किसी गोलाकार सतह से प्रतिच्छेद न कर ले, तब तक कहलाता है ऊंचाईगेंद खंड. डॉटएम बुलाया शीर्षगेंद खंड.

दो समान्तर तलों के बीच घिरे गोले का भागएबीसी और डीईएफ एक गोलाकार सतह को काटते हैं (चित्र 93), बुलाया गोलाकार परत; गोलाकार परत की घुमावदार सतह कहलाती है बॉल बेल्ट(क्षेत्र). मंडलियां एबीसी और डीईएफ – मैदानबॉल बेल्ट. दूरीएन.के. गोलाकार बेल्ट के आधारों के बीच - इसका ऊंचाई. गोलाकार खंड की घुमावदार सतह से घिरा गेंद का भाग (एएमसीबी, चित्र 93) और शंक्वाकार सतह OABC , जिसका आधार खंड का आधार है (एबीसी ), और शीर्ष गेंद का केंद्र हैहे , बुलाया गोलाकार क्षेत्र.

जब लोगों से गोले और गेंद के बीच अंतर पूछा जाता है, तो कई लोग यह सोचकर अपने कंधे उचकाते हैं कि वास्तव में वे एक ही चीज़ हैं (एक वृत्त और एक वृत्त के साथ सादृश्य)। दरअसल, क्या हम सभी स्कूली पाठ्यक्रम से ज्यामिति को अच्छी तरह से जानते हैं और तुरंत इस प्रश्न का उत्तर दे सकते हैं? एक गोले में एक गेंद से कुछ अंतर होते हैं, जिन्हें न केवल स्कूली बच्चों को अपने प्रदर्शित ज्ञान के लिए अच्छा ग्रेड प्राप्त करने के लिए जानना आवश्यक है, बल्कि कई अन्य लोगों को भी, उदाहरण के लिए, जिनका काम सीधे चित्र बनाने से संबंधित है।

परिभाषा

गेंद- अंतरिक्ष में सभी बिंदुओं का समुच्चय। ये सभी बिंदु ज्यामितीय निकाय के केंद्र से इतनी दूरी पर स्थित हैं कि दी गई दूरी से अधिक नहीं है। यह दूरी ही त्रिज्या कहलाती है। एक गेंद, एक ज्यामितीय पिंड के रूप में, इस प्रकार बनती है: एक अर्धवृत्त इसके व्यास के पास घूमता है। जहाँ तक गोले की बात है, यह गेंद की सतह है (उदाहरण के लिए, एक बंद गेंद में यह शामिल है, एक खुली गेंद में नहीं)। किसी गेंद के क्षेत्रफल या आयतन की गणना में संपूर्ण ज्यामितीय सूत्र शामिल होते हैं जो ज्यामितीय आकृति की स्पष्ट सादगी के बावजूद, बहुत जटिल होते हैं।

गोला, जैसा कि ऊपर बताया गया है, गेंद की सतह, उसका खोल है। अंतरिक्ष में सभी बिंदु गोले के केंद्र से समान दूरी पर हैं। जहाँ तक एक ज्यामितीय पिंड की त्रिज्या का सवाल है, इसे कोई भी खंड कहा जाता है, जिसका एक बिंदु सीधे गोले का केंद्र होता है, और दूसरा सतह पर किसी भी बिंदु पर स्थित हो सकता है। हम कह सकते हैं कि गोला बिना किसी सामग्री वाली गेंद का खोल है (अधिक विशिष्ट उदाहरण नीचे दिए जाएंगे)। एक गेंद की तरह, एक गोला क्रांति का एक पिंड है। वैसे, कई लोग यह भी सोचते हैं कि एक वृत्त और एक वृत्त और एक गोले और एक गेंद में क्या अंतर है। यहां सब कुछ सरल है: पहले मामले में ये एक विमान पर आंकड़े हैं, दूसरे में - अंतरिक्ष में।

तुलना

यह पहले ही कहा जा चुका है कि गोला एक गेंद की सतह है, जो पहले से ही अंतर के एक महत्वपूर्ण संकेत के बारे में बात करना संभव बनाता है। दो ज्यामितीय निकायों के बीच अंतर कुछ अन्य पहलुओं में देखा जाता है:

• गेंद के सभी बिंदु केंद्र से समान दूरी पर हैं, जबकि शरीर सतह (एक गोला जो अंदर खाली है) द्वारा सीमित है। दूसरे शब्दों में, गोला खोखला है। आमतौर पर, समझने में आसानी के लिए, गुब्बारे और बिलियर्ड गेंद का एक सरल उदाहरण दिया जाता है। इन दोनों वस्तुओं को गेंद कहा जाता है, लेकिन पहले मामले में हम एक गोले के साथ काम कर रहे हैं, और दूसरे में एक पूर्ण विकसित गेंद के साथ, जिसके अंदर अपनी सामग्री है।
• गोले का अपना क्षेत्रफल तो होता है, परन्तु उसका कोई आयतन नहीं होता। एक गोला इसके विपरीत है: इसके आयतन की गणना की जा सकती है, जबकि इसका कोई क्षेत्रफल नहीं है। कुछ लोग कह सकते हैं कि यह अंतर का मुख्य संकेत है, लेकिन यह केवल तभी प्रकट होता है जब कुछ गणनाएँ (जटिल ज्यामितीय सूत्र) करना आवश्यक हो। इसलिए, मुख्य अंतर यह है कि गोला खोखला है, और गेंद एक पिंड है जिसके अंदर सामग्री है।
• एक और अंतर त्रिज्या में है. उदाहरण के लिए, किसी गोले की त्रिज्या केवल उसके केंद्र से बिंदुओं की दूरी नहीं है। त्रिज्या किसी गोले पर किसी बिंदु को उसके केंद्र से जोड़ने वाला कोई भी खंड हो सकता है। ये सभी खंड एक दूसरे के बराबर हैं। जहाँ तक गेंद की बात है, इसके अंदर स्थित बिंदु एक त्रिज्या से भी कम दूरी पर केंद्र से हट जाते हैं (ठीक इसलिए क्योंकि गोला इसे घेरे हुए है)।

निष्कर्ष वेबसाइट

1. गोला खोखला होता है, जबकि गेंद अंदर भरा हुआ पिंड होता है। उदाहरण के लिए, गर्म हवा का गुब्बारा एक गोला है, बिलियर्ड गेंद एक पूर्ण विकसित गेंद है।
2. एक गोले का क्षेत्रफल होता है और उसका कोई आयतन नहीं होता, लेकिन एक गोले का कार्य इसके विपरीत होता है।
3. तीसरा अंतर दो ज्यामितीय निकायों की त्रिज्या का माप है।

परिभाषा।

एक गोले को एक त्रि-आयामी आकृति के रूप में वर्णित किया जा सकता है जो इसके व्यास के चारों ओर 180° तक एक वृत्त घुमाने या इसके व्यास के चारों ओर 360° तक अर्धवृत्त घुमाने से बनता है।

परिभाषा।

एक गेंद को एक त्रि-आयामी आकृति के रूप में वर्णित किया जा सकता है जो इसके व्यास के चारों ओर 180° तक एक वृत्त घुमाने या इसके व्यास के चारों ओर 360° तक अर्धवृत्त घुमाने से बनती है।

परिभाषा। गोले की त्रिज्या (गेंद)(R) गोले (गेंद) के केंद्र से दूरी है हेगोले के किसी भी बिंदु (गेंद की सतह) पर।

परिभाषा। गोला (गेंद) व्यास(डी) एक गोले के दो बिंदुओं (गेंद की सतह) को जोड़ने वाला और उसके केंद्र से गुजरने वाला एक खंड है।

सूत्र. गोला आयतन:

सूत्र. एक गोले का सतह क्षेत्रत्रिज्या या व्यास के माध्यम से:

एस = 4π आर 2 = π डी 2

क्षेत्र समीकरण

1. कार्टेशियन समन्वय प्रणाली के मूल में त्रिज्या आर और केंद्र के साथ एक गोले का समीकरण:

एक्स 2 + वाई 2 + जेड 2 = आर 2

2. कार्टेशियन समन्वय प्रणाली में निर्देशांक (x 0, y 0, z 0) के साथ एक बिंदु पर केंद्र और त्रिज्या R वाले एक गोले का समीकरण:

(एक्स - एक्स 0) 2 + (वाई - वाई 0) 2 + (जेड - जेड 0) 2 = आर 2

परिभाषा। बिल्कुल विपरीत बिंदुगेंद (गोले) की सतह पर कोई दो बिंदु होते हैं जो एक व्यास से जुड़े होते हैं।

एक गोले और एक गेंद के मूल गुण

1. गोले के सभी बिंदु केंद्र से समान दूरी पर हैं।

2. किसी गोले का समतल द्वारा काटा गया कोई भी भाग एक वृत्त होता है।

3. समतल द्वारा गेंद का कोई भी भाग एक वृत्त होता है।

4. समान सतह क्षेत्रफल वाली सभी स्थानिक आकृतियों में गोले का आयतन सबसे अधिक है।

5. किन्हीं दो बिल्कुल विपरीत बिंदुओं के माध्यम से आप एक गोले के लिए कई बड़े वृत्त या एक गेंद के लिए वृत्त खींच सकते हैं।

6. व्यास के विपरीत बिंदुओं को छोड़कर किन्हीं दो बिंदुओं से होकर, आप गोले के लिए केवल एक बड़ा वृत्त या गेंद के लिए एक बड़ा वृत्त खींच सकते हैं।

7. एक गेंद के कोई भी दो बड़े वृत्त गेंद के केंद्र से गुजरने वाली एक सीधी रेखा के साथ प्रतिच्छेद करते हैं, और वृत्त दो बिल्कुल विपरीत बिंदुओं पर प्रतिच्छेद करते हैं।

8. यदि किन्हीं दो गेंदों के केन्द्रों के बीच की दूरी उनकी त्रिज्याओं के योग से कम और उनकी त्रिज्याओं के अंतर के मापांक से अधिक हो, तो ऐसी गेंदें इंटरसेक्ट, और प्रतिच्छेदन तल में एक वृत्त बनता है।

गोले का छेदक, जीवा, छेदक तल और उनके गुण

परिभाषा। गोला छेदकएक सीधी रेखा है जो गोले को दो बिंदुओं पर काटती है। प्रतिच्छेदन बिंदु कहलाते हैं छेदने वाले बिंदुसतह या सतह पर प्रवेश और निकास बिंदु।

परिभाषा। गोले की जीवा (गेंद)- यह एक गोले (गेंद की सतह) पर दो बिंदुओं को जोड़ने वाला एक खंड है।

परिभाषा। विमान काटनावह तल है जो गोले को काटता है।

परिभाषा। व्यास तल- यह एक गोले या गेंद के केंद्र से गुजरने वाला एक छेदक तल है, अनुभाग तदनुसार बनता है बड़ा वृत्तऔर दीर्घ वृत्ताकार. वृहत वृत्त और वृहत वृत्त का एक केंद्र होता है जो गोले (गेंद) के केंद्र से मेल खाता है।

गोले (गेंद) के केंद्र से गुजरने वाली कोई भी जीवा एक व्यास है।

जीवा एक छेदक रेखा का एक खंड है।

गोले के केंद्र से छेदक तक की दूरी d हमेशा गोले की त्रिज्या से कम होती है:

डी< R

काटने वाले तल और गोले के केंद्र के बीच की दूरी m हमेशा त्रिज्या R से कम होती है:

एम< R

गोले पर काटने वाले तल के अनुभाग का स्थान सदैव रहेगा छोटा वृत्त, और गेंद पर अनुभाग होगा छोटा वृत्त. छोटे वृत्त और छोटे वृत्त के अपने-अपने केंद्र होते हैं जो गोले (गेंद) के केंद्र से मेल नहीं खाते हैं। ऐसे वृत्त की त्रिज्या r सूत्र का उपयोग करके ज्ञात की जा सकती है:

आर = √आर 2 - मी 2,

जहाँ R गोले (गेंद) की त्रिज्या है, m गेंद के केंद्र से काटने वाले तल तक की दूरी है।

परिभाषा। गोलार्ध (गोलार्ध)- यह एक गोले (गेंद) का आधा भाग है, जो एक व्यासीय तल से काटने पर बनता है।

स्पर्शरेखा, गोले का स्पर्शरेखा तल और उनके गुण

परिभाषा। एक गोले की स्पर्शरेखाएक सीधी रेखा है जो गोले को केवल एक बिंदु पर स्पर्श करती है।

परिभाषा। एक गोले का स्पर्शरेखा तलएक समतल है जो गोले को केवल एक बिंदु पर स्पर्श करता है।

स्पर्शरेखा रेखा (तल) हमेशा संपर्क बिंदु पर खींचे गए गोले की त्रिज्या के लंबवत होती है

गोले के केंद्र से स्पर्श रेखा (तल) की दूरी गोले की त्रिज्या के बराबर होती है।

परिभाषा। गेंद खंड- यह गेंद का वह भाग है जो कटिंग प्लेन द्वारा गेंद से काटा जाता है। खंड का आधारअनुभाग के स्थल पर बनने वाले वृत्त को कहते हैं। खंड की ऊंचाई h खंड के आधार के मध्य से खंड की सतह तक खींचे गए लंबवत की लंबाई है।

सूत्र. किसी गोले खंड का बाहरी सतह क्षेत्रगोले की त्रिज्या के माध्यम से ऊँचाई h के साथ R:

एस = 2πRh