1 в параллелограмме противоположные углы. Параллелограмм

Доказательство

Первым делом проведем диагональ AC . Получаются два треугольника: ABC и ADC .

Так как ABCD — параллелограмм, то справедливо следующее:

AD || BC \Rightarrow \angle 1 = \angle 2 как лежащие накрест.

AB || CD \Rightarrow \angle3 = \angle 4 как лежащие накрест.

Следовательно, \triangle ABC = \triangle ADC (по второму признаку: и AC — общая).

И, значит, \triangle ABC = \triangle ADC , то AB = CD и AD = BC .

Доказано!

2. Противоположные углы тождественны.

Доказательство

Согласно доказательству свойства 1 мы знаем, что \angle 1 = \angle 2, \angle 3 = \angle 4 . Таким образом сумма противоположных углов равна: \angle 1 + \angle 3 = \angle 2 + \angle 4 . Учитывая, что \triangle ABC = \triangle ADC получаем \angle A = \angle C , \angle B = \angle D .

Доказано!

3. Диагонали разделены пополам точкой пересечения.

Доказательство

Проведем еще одну диагональ.

По свойству 1 мы знаем, что противоположные стороны тождественны: AB = CD . Еще раз отметим накрест лежащие равные углы.

Таким образом видно, что \triangle AOB = \triangle COD по второму признаку равенства треугольников (два угла и сторона между ними). То есть, BO = OD (напротив углов \angle 2 и \angle 1 ) и AO = OC (напротив углов \angle 3 и \angle 4 соответственно).

Доказано!

Признаки параллелограмма

Если лишь один признак в вашей задаче присутствует, то фигура является параллелограммом и можно использовать, все свойства данной фигуры.

Для лучшего запоминания, заметим, что признак параллелограмма будет отвечать на следующий вопрос — «как узнать?» . То есть, как узнать, что заданная фигура это параллелограмм.

1. Параллелограммом является такой четырехугольник, у которого две стороны равны и параллельны.

AB = CD ; AB || CD \Rightarrow ABCD — параллелограмм.

Доказательство

Рассмотрим подробнее. Почему AD || BC ?

\triangle ABC = \triangle ADC по свойству 1 : AB = CD , AC — общая и \angle 1 = \angle 2 как накрест лежащие при параллельных AB и CD и секущей AC .

Но если \triangle ABC = \triangle ADC , то \angle 3 = \angle 4 (лежат напротив AB и CD соответственно). И следовательно AD || BC (\angle 3 и \angle 4 - накрест лежащие тоже равны).

Первый признак верен.

2. Параллелограммом является такой четырехугольник, у которого противоположные стороны равны.

AB = CD , AD = BC \Rightarrow ABCD — параллелограмм.

Доказательство

Рассмотрим данный признак. Еще раз проведем диагональ AC .

По свойству 1 \triangle ABC = \triangle ACD .

Из этого следует, что: \angle 1 = \angle 2 \Rightarrow AD || BC и \angle 3 = \angle 4 \Rightarrow AB || CD , то есть ABCD — параллелограмм.

Второй признак верен.

3. Параллелограммом является такой четырехугольник, у которого противоположные углы равны.

\angle A = \angle C , \angle B = \angle D \Rightarrow ABCD — параллелограмм.

Доказательство

2 \alpha + 2 \beta = 360^{\circ} (поскольку ABCD — четырехугольник, а \angle A = \angle C , \angle B = \angle D по условию).

Получается, \alpha + \beta = 180^{\circ} . Но \alpha и \beta являются внутренними односторонними при секущей AB .

И то, что \alpha + \beta = 180^{\circ} говорит и о том, что AD || BC .

При этом \alpha и \beta — внутренние односторонние при секущей AD . И это значит AB || CD .

Третий признак верен.

4. Параллелограммом является такой четырехугольник, у которого диагонали разделены точкой пересечения пополам.

AO = OC ; BO = OD \Rightarrow параллелограмм.

Доказательство

BO = OD ; AO = OC , \angle 1 = \angle 2 как вертикальные \Rightarrow \triangle AOB = \triangle COD , \Rightarrow \angle 3 = \angle 4 , и \Rightarrow AB || CD .

Аналогично BO = OD ; AO = OC , \angle 5 = \angle 6 \Rightarrow \triangle AOD = \triangle BOC \Rightarrow \angle 7 = \angle 8 , и \Rightarrow AD || BC .

Четвертый признак верен.

Муниципальное бюджетное общеобразовательное учреждение

Савинская средняя общеобразовательная школа

Исследовательская работа

Параллелограмм и его новые свойства

Выполнила: ученица 8Б класса

МБОУ Савинская СОШ

Кузнецова Светлана,14 лет

Руководитель: учитель математики

Тульчевская Н.А.

п. Савино

Ивановская область, Россия

2016г.

I . Введение __________________________________________________стр 3

II . Из истории параллелограмма ___________________________________стр 4

III Дополнительные свойства параллелограмма ______________________стр 4

IV . Доказательство свойств _____________________________________ стр 5

V . Решение задач с использованием дополнительных свойств __________стр 8

VI . Применение свойств параллелограмма в жизни ___________________стр 11

VII . Заключение _________________________________________________стр 12

VIII . Литература _________________________________________________стр 13

Введение

"Среди равных умов

при одинаковости прочих условий

превосходит тот, кто знает геометрию"

(Блез Паскаль).

Во время изучения темы «Параллелограмм» на уроках геометрии мы рассмотрели два свойства параллелограмма и три признака, но когда мы начали решать задачи, то оказалось, что этого недостаточно.

У меня возник вопрос, а есть ли у параллелограмма еще свойства, и как они помогут при решении задач.

И я решила изучить дополнительные свойства параллелограмма и показать, как их можно применить для решения задач.

Предмет исследования : параллелограмм

Объект исследования : свойства параллелограмма
Цель работы:

формулировка и доказательство дополнительных свойств параллелограмма, которые не изучаются в школе;

применение этих свойств для решения задач.

Задачи:

Изучить историю возникновения параллелограмма и историю развития его свойств;

Найти дополнительную литературу по исследуемому вопросу;

Изучить дополнительные свойства параллелограмма и доказать их;

Показать применение этих свойств для решения задач;

Рассмотреть применение свойств параллелограмма в жизни.
Методы исследования:

Работа с учебной и научно – популярной литературой, ресурсами сети Интернет;

Изучение теоретического материала;

Выделение круга задач, которые можно решать с использованием дополнительных свойств параллелограмма;

Наблюдение, сравнение, анализ, аналогия.

Продолжительность исследования : 3 месяца: январь-март 2016г

В учебнике геометрии мы читаем следующее определение параллелограмма: параллелограмм – это такой четырехугольник, у которого противоположные стороны попарно параллельны

Слово «параллелограмм» переводится как «параллельные линии» (от греческих слов Parallelos - параллельный и gramme - линия), этот термин был введен Евклидом. В своей книге «Начала» Евклид доказал следующие свойства параллелограмма: противоположные стороны и углы параллелограмма равны, а диагональ делит его пополам. О точке пересечения параллелограмма Евклид не упоминает. Только к концу средних веков была разработана полная теория параллелограммов И лишь в XVII веке в учебниках появились теоремы о параллелограммах, которые доказываются с помощью теоремы Евклида о свойствах параллелограмма.

III Дополнительные свойства параллелограмма

В учебнике по геометрии даны только 2 свойства параллелограмма:

Противоположные углы и стороны равны

Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам

В различных источниках по геометрии можно встретить следующие дополнительные свойства:

Сумма соседних углов параллелограмма равна 180 0

Биссектриса угла параллелограмма отсекает от него равнобедренный треугольник;

Биссектрисы противоположных углов параллелограмма лежат на параллельных прямых;

Биссектрисы соседних углов параллелограмма пересекаются под прямым углом;

Биссектрисы всех углов параллелограмма при пересечении образуют прямоугольник;

Расстояния от противоположных углов параллелограмма до одной и той же его диагонали равны.

Если в параллелограмме соединить противоположные вершины с серединами противоположных сторон, то получится еще один параллелограмм.

Сумма квадратов диагоналей параллелограмма равна удвоенной сумме квадратов его смежных сторон.

Если в параллелограмме из двух противоположных углов провести высоты, то получится прямоугольник.

IV Доказательство свойств параллелограмма

Сумма соседних углов параллелограмма равна 180 0

Дано :

ABCD – параллелограмм

Доказать:

A +
B =

Доказательство:

А и
B –внутренние односторонние углы при параллельных прямых ВС АD и секущей АВ, значит,
A +
B =

Дано: АBCD - параллелограмм,

АК -биссектриса
А.

Доказать: АВК – равнобедренный

Доказательство:

1)
1=
3 (накрест лежащие при ВСAD и секущей AK ),

2)
2=
3 т. к. АК – биссектриса,

значит 1=
2.

3) АВК – равнобедренный т. к. 2 угла треугольника равны

. Биссектриса угла параллелограмма отсекает от него равнобедренный треугольник

Дано: АВСD – параллелограмм,

АК – биссектриса A,

СР - биссектриса C.

Доказать: АК ║ СР

Доказательство:

1) 1=2 т. к. АК-биссектриса

2) 4=5 т.к. СР – биссектриса

3) 3=1 (накрест лежащие углы при

ВС ║ АD и АК-секущей),

4) A =C (по свойству параллелограмма), значит2=3=4=5.

4) Из п. 3 и 4 следует, что 1=4, а эти углы соответственные при прямых АК и СР и секущей ВС,

значит, АК ║ СР (по признаку параллельности прямых)

. Биссектрисы противоположных углов параллелограмма лежат на параллельных прямых

Биссектрисы соседних углов параллелограмма пересекаются под прямым углом

Дано: АВСD - параллелограмм,

АК-биссектриса A,

DР-биссектриса D

Доказать: DР АК.

Доказательство:

1) 1=2, т.к. АК - биссектриса

Пусть, 1=2=x, тогда А=2x,

2) 3=4, т.к. D Р – биссектриса

Пусть, 3=4= у, тогда D =2y

3) A +D =180 0 , т.к. сумма соседних углов параллелограмма равна 180

2) Рассмотрим A ОD

1+3=90 0 , тогда
<5=90 0 (сумма углов треугольников равна 180 0)

5. Биссектрисы всех углов параллелограмма при пересечении образуют прямоугольник

Дано: АВСD - параллелограмм, АК-биссектриса A,

DР-биссектриса D,

CM -биссектриса C ,

BF -биссектриса B .

Доказать : KRNS -прямоугольник

Доказательство:

Исходя из предыдущего свойства 8=7=6=5=90 0 ,

значит KRNS -прямоугольник.

Расстояния от противоположных углов параллелограмма до одной и той же его диагонали равны.

Дано: ABCD-параллелограмм, АС-диагональ.

ВК АС, DPAC

Доказать: BК=DР

Доказательство: 1)DCР=КAB, как внутренние накрест лежащие при АВ ║ СD и секущей АС.

2) AКB=CDР (по стороне и двум прилежащим к ней углам АВ=СD CD Р=AB К).

А в равных треугольниках соответственные стороны равны, значит DР=BК.

Дано: ABCD-параллелограмм.

Доказать: ВКDР – параллелограмм.

Доказательство:

1) BР=КD (AD=BC, точки К и Р

делят эти стороны пополам)

2) ВР ║ КD (лежат на АD BC)

Если в четырехугольнике противоположные стороны равны и параллельны, значит, этот четырехугольник -параллелограмм.

Если в параллелограмме из двух противоположных углов провести высоты, то получится прямоугольник.

Сумма квадратов диагоналей параллелограмма равна удвоенной сумме квадратов его смежных сторон.

Дано: ABCD – параллелограмм. BD и AC - диагонали.

Доказать: АС 2 +ВD 2 =2(AB 2 + AD 2 )

Доказательство: 1)АСК: AC ²=
+

2)B Р D : BD 2 = B Р 2 + Р D 2 (по теореме Пифагора)

3) AC ²+ BD ²=СК²+ A К²+ B Р²+Р D ²

4) СК = ВР = Н (высота)

5) АС 2 +В D 2 = H 2 + A К 2 + H 2 +Р D 2

6) Пусть D К= A Р=х , тогда C К D : H 2 = CD 2 – х 2 по теореме Пифагора)

7) АС²+В D ² = С D 2 - х²+ АК 1 ²+ CD 2 -х 2 +Р D 2 ,

АС²+В D ²=2С D 2 -2х 2 + A К 2 +Р D 2

8) A К =AD+ х , Р D=AD- х ,

АС²+В D ² =2 CD 2 -2х 2 +(AD +х) 2 +(AD -х) 2 ,

АС ²+ В D²=2 С D²-2 х ² +AD 2 +2AD х + х 2 +AD 2 -2AD х + х 2 ,
АС ²+ В D²=2CD 2 +2AD 2 =2(CD 2 +AD 2 ).

V . Решение задач с использованием этих свойств

Точка пересечения биссектрис двух углов параллелограмма, прилежащих к одной стороне, принадлежит противоположной стороне. Меньшая сторона параллелограмма равна 5 . Найдите его большую сторону.

Дано: ABCD – параллелограмм,

АК – биссектриса
А,

D К – биссектриса
D , АВ=5

Найти : ВС

ешение

Решение

Т.к. АК - биссектриса
А, то АВК – равнобедренный.

Т.к. D К – биссектриса
D , то DCK - равнобедренный

DC =C К= 5

Тогда, ВС=ВК+СК=5+5 = 10

Ответ: 10

2. Найдите периметр параллелограмма, если биссектриса одного из его углов делит сторону параллелограмма на отрезки 7 см и 14 см.

1 случай

Дано:
А,

ВК=14 см, КС=7 см

Найти: Р параллелограмма

Решение

ВС=ВК+КС=14+7=21 (см)

Т.к. АК – биссектриса
А, то АВК – равнобедренный.

АВ=ВК= 14 см

Тогда Р=2 (14+21) =70 (см)

случай

Дано: ABCD – параллелограмм,

D К – биссектриса
D ,

ВК=14 см, КС=7 см

Найти : Р параллелограмма

Решение

ВС=ВК+КС=14+7=21 (см)

Т.к. D К – биссектриса
D , то DCK - равнобедренный

DC =C К= 7

Тогда, Р= 2 (21+7) = 56 (см)

Ответ: 70см или 56 см

3.Стороны параллелограмма равны 10 см и 3 см. Биссектрисы двух углов, прилежащих к большей стороне, делят противоположную сторону на три отрезка. Найдите эти отрезки.

1 случай: биссектрисы пересекаются вне параллелограмма

Дано: ABCD – параллелограмм, АК – биссектриса
А,

D К – биссектриса
D , АВ=3 см, ВС=10 см

Найти : ВМ, МN , NC

Решение

Т.к. АМ - биссектриса
А, то АВМ – равнобедренный.

Т.к. DN – биссектриса
D , то DCN - равнобедренный

DC =CN = 3

Тогда, МN = 10 – (BM +NC ) = 10 – (3+3)=4 см

2 случай: биссектрисы пересекаются внутри параллелограмма

Т.к. АN - биссектриса
А, то АВN – равнобедренный.

АВ=В N = 3 D

А раздвижную решетку – отодвигать на необходимое расстояние в дверном проеме

Параллелограммный механизм - четырёхзвенный механизм, звенья которого составляют параллелограмм. Применяется для реализации поступательного движения шарнирными механизмами.

Параллелограмм с неподвижным звеном - одно звено неподвижно, противоположное совершает качательное движение, оставаясь параллельным неподвижному. Два параллелограмма, соединённых друг за другом, дают конечному звену две степени свободы, оставляя его параллельным неподвижному.

Примеры: стеклоочистители автобусов, погрузчики, штативы, подвесы, автомобильные подвески.

Параллелограмм с неподвижным шарниром - используется свойство параллелограмма сохранять постоянное соотношение расстояний между тремя точками. Пример: чертёжный пантограф - прибор для масштабирования чертежей.

Ромб - все звенья одинаковой длины, приближение (стягивание) пары противоположных шарниров приводит к раздвиганию двух других шарниров. Все звенья работают на сжатие.

Примеры - автомобильный ромбовидный домкрат, трамвайный пантограф.

Ножничный или X-образный механизм , также известный как Нюрнбергские ножницы - вариант ромба - два звена, соединённые посередине шарниром. Достоинства механизма - компактность и простота, недостаток - наличие двух пар скольжения. Два (и более) таких механизма, соединённые последовательно, образуют в середине ромб(ы). Применяется в подъёмниках, детских игрушках.

VII Заключение

Кто с детских лет занимается математикой,

тот развивает внимание, тренирует свой мозг,

свою волю, воспитывает в себе настойчивость

и упорство в достижении цели

А. Маркушевич

В ходе работы я доказала дополнительные свойства параллелограмма.

Я убедилась, что применяя эти свойства, можно решать задачи быстрее.

Я показала, как применяются эти свойства на примерах решения конкретных задач.

Я узнала много нового о параллелограмме, чего нет в нашем учебнике геометрии

Я убедилась в том, что знания геометрии очень важны в жизни на примерах применения свойств параллелограмма.

Цель моей исследовательской работы выполнена.

О том, насколько важны математические знания, говорит тот факт, что была учреждена премия тому, кто издаст книгу о человеке, который всю жизнь прожил без помощи математики. Эту премию до сих пор не получил ни один человек.

VIII Литература

Параллелограмм - четырехугольник, у которого противоположные стороны попарно параллельны. Площадь параллелограмма равна произведению его основания (a) на высоту (h). Также можно найте его площадь через две стороны и угол и через диагонали.

Свойства параллелограмма

1. Противоположные стороны тождественны

Первым делом проведем диагональ \(AC \) . Получаются два треугольника: \(ABC \) и \(ADC \) .

Так как \(ABCD \) - параллелограмм, то справедливо следующее:

\(AD || BC \Rightarrow \angle 1 = \angle 2 \) как лежащие накрест.

\(AB || CD \Rightarrow \angle3 = \angle 4 \) как лежащие накрест.

Следовательно, (по второму признаку: и \(AC \) - общая).

И, значит, \(\triangle ABC = \triangle ADC \) , то \(AB = CD \) и \(AD = BC \) .

2. Противоположные углы тождественны

Согласно доказательству свойства 1 мы знаем, что \(\angle 1 = \angle 2, \angle 3 = \angle 4 \) . Таким образом сумма противоположных углов равна: \(\angle 1 + \angle 3 = \angle 2 + \angle 4 \) . Учитывая, что \(\triangle ABC = \triangle ADC \) получаем \(\angle A = \angle C \) , \(\angle B = \angle D \) .

3. Диагонали разделены пополам точкой пересечения

По свойству 1 мы знаем, что противоположные стороны тождественны: \(AB = CD \) . Еще раз отметим накрест лежащие равные углы.

Таким образом видно, что \(\triangle AOB = \triangle COD \) по второму признаку равенства треугольников (два угла и сторона между ними). То есть, \(BO = OD \) (напротив углов \(\angle 2 \) и \(\angle 1 \) ) и \(AO = OC \) (напротив углов \(\angle 3 \) и \(\angle 4 \) соответственно).

Признаки параллелограмма

Для лучшего запоминания, заметим, что признак параллелограмма будет отвечать на следующий вопрос - «как узнать?» . То есть, как узнать, что заданная фигура это параллелограмм.

1. Параллелограммом является такой четырехугольник, у которого две стороны равны и параллельны

\(AB = CD \) ; \(AB || CD \Rightarrow ABCD \) - параллелограмм.

Рассмотрим подробнее. Почему \(AD || BC \) ?

\(\triangle ABC = \triangle ADC \) по свойству 1 : \(AB = CD \) , \(\angle 1 = \angle 2 \) как накрест лежащие при параллельных \(AB \) и \(CD \) и секущей \(AC \) .

Но если \(\triangle ABC = \triangle ADC \) , то \(\angle 3 = \angle 4 \) (лежат напротив \(AD || BC \) (\(\angle 3 \) и \(\angle 4 \) - накрест лежащие тоже равны).

Первый признак верен.

2. Параллелограммом является такой четырехугольник, у которого противоположные стороны равны

\(AB = CD \) , \(AD = BC \Rightarrow ABCD \) - параллелограмм.

Рассмотрим данный признак. Еще раз проведем диагональ \(AC \) .

По свойству 1 \(\triangle ABC = \triangle ACD \) .

Из этого следует, что: \(\angle 1 = \angle 2 \Rightarrow AD || BC \) и \(\angle 3 = \angle 4 \Rightarrow AB || CD \) , то есть \(ABCD \) - параллелограмм.

Второй признак верен.

3. Параллелограммом является такой четырехугольник, у которого противоположные углы равны

\(\angle A = \angle C \) , \(\angle B = \angle D \Rightarrow ABCD \) - параллелограмм.

\(2 \alpha + 2 \beta = 360^{\circ} \) (поскольку \(\angle A = \angle C \) , \(\angle B = \angle D \) по условию).

Получается, . Но \(\alpha \) и \(\beta \) являются внутренними односторонними при секущей \(AB \) .

И то, что \(\alpha + \beta = 180^{\circ} \) говорит и о том, что \(AD || BC \) .

Параллелограммом называется четырехугольник, у которго противоположные стороны параллельны, т.е. лежат на параллельных прямых

Свойства параллелограмма: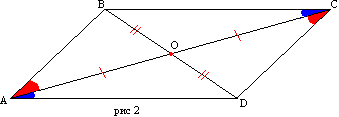
Теорема 22. Противоположные стороны параллелограма равны.
Доказательство. В параллелограмме АВСD проведем диагональ АС. Треугольники АСD и АСВ равны, как имеющие общую сторону АС и две пары равных углов. прилежащих к ней: ∠ САВ=∠ АСD, ∠ АСВ=∠ DAC (как накрест лежащие углы при параллельных прямых AD и ВС). Значит, АВ=CD и ВС=AD, как соответственные стороны равных треугольников, ч.т.д. Из равенства этих треугольников также следует равенство соответственных углов треугольников:
Теорема 23. Противоположные углы параллелограмма равны: ∠ А=∠ С и ∠ В=∠ D.
Равенство первой пары идет из равенства треугольников АВD и CBD, а второй - АВС и ACD.
Теорема 24. Соседние углы параллелограмма, т.е. углы, прилежащие к одной стороне, составляют в сумме 180 градусов.
Это так, потому что они являются внутренними односторонними углами.
Теорема 25. Диагонали параллелограмма делят друг друга в точке их пересечения пополам.
Доказательство. Рассмотрим треугольники ВОС и АОD. По первому свойству AD=ВС ∠ ОАD=∠ ОСВ и ∠ ОDА=∠ ОВС как накрест лежащие при параллельных прямых AD и ВС. Поэтому треугольники ВОС и АОD равны по стороне и прилежащим к ней углам. Значит, ВО=ОD и АО=ОС, как соответственные стороны равных треугольников, ч.т.д.

Признаки параллелограмма
Теорема 26. Если противоположные стороны четырехугольника попарно равны, то он является параллелограммом.
Доказательство. Пусть у четырехугольника АВСD стороны AD и ВС, АВ и CD соответственно равны (рис2). Проведем диагональ АС. Треугольникик АВС и ACD равны по трем сторонам. Тогда углы ВАС и DСА равны и, следовательно, АВ параллельна CD. Параллельность сторон ВС и AD следует из равенства углов CAD и АСВ.
Теорема 27. Если противоположные углы четырехугольника попарно равны, то он является параллелограммом.
Пусть ∠ А=∠ С и ∠ В=∠ D. Т.к. ∠ А+∠ В+∠ С+∠ D=360 о, то ∠ А+∠ В=180 о и стороны AD и ВС параллельны (по признаку параллельности прямых). Также докажем и параллельность сторон АВ и CD и заключим, что АВСD является параллелограммом по определению.
Теорема 28. Если соседние углы четырехугольника, т.е. углы, прилежащие к одной стороне, составляют в сумме 180 градусов, то он является параллелограммом.
Если внутренние односторонные углы в сумме составляют 180 градусов, то прямые праллельны. Значит АВ парал CD и ВС парал AD. Четырехугольник оказывается параллелограммом по определению.
Теорема 29. Если диагонали четырехугольника взаимно делятся в точке пересечения пополам, то четырехугольник - параллелограмм.
Доказательство. Если АО=ОС, ВО=ОD, то треугольники АOD и ВОС равны, как имеющие равны углы (вертикальные) при вершине О, заключенные между парами равных сторон. Из равенства треугольников заключаем, что AD и ВС равны. Также равны стороны АВ и CD, и четырехугольник оказывается параллелограммом по признаку 1.
Теорема 30. Если четырехугольник имеет пару равных, параллельных между собой сторон, то он является параллелограммом.
Пусть в четырехугольнике АВСD стороны АВ и CD параллельны и равны. Проведем диагонали АС и ВD. Из параллельности этих прямых следует равенство накрест лежащих углов АВО=СDО и ВАО=ОСD. Треугольники АВО и CDО равны по стороне и прилежащим к ней углам. Поэтому АО=ОС, ВО=ОD, т.е. диагонали точкой пересечения делятся пополам и четырехугольник оказывается параллелограммом по признаку 4.

В геометрии рассматривают частные случаи параллелограмма.

Параллелограмм - это четырехугольник, у которого противоположные стороны попарно параллельны. На следующем рисунке представлен параллелограмм ABCD. У него сторона AB параллельна стороне CD, а сторона BC параллельна стороне AD.

Как вы уже успели догадаться, параллелограмм является выпуклым четырехугольником. Рассмотрим основные свойства параллелограмма.

Свойства параллелограмма

1. В параллелограмме противоположные углы и противоположные стороны равны. Докажем это свойство - рассмотрим параллелограмм, представленный на следующем рисунке.

Диагональ BD разделяет его на два равных треугольника: ABD и CBD. Они равны по стороне BD и двум прилежащим к ней углам, так как углы накрест лежащие при секущей BD параллельных прямых BC и AD и AB и CD соответственно. Следовательно, AB = CD и
BC = AD. А из равенства углов 1, 2 ,3 и 4 следует, что угол A = угол1 +угол3 = угол2 + угол4 = угол С.

2. Диагонали параллелограмма точкой пересечения делятся пополам. Пусть точка О есть точка пересечения диагоналей AC и BD параллелограмма ABCD.

Тогда треугольник AOB и треугольник COD равны между собой, по стороне и двум прилежащим к ней углам. (AB=CD так как это противоположные стороны параллелограмма. А угол1 = угол2 и угол3 = угол4 как накрест лежащие углы при пересечении прямых AB и CD секущими AC и BD соответственно.) Из этого следует, что AO = OC и OB = OD, что и требовалось доказать.

Все основные свойства проиллюстрированы на следующих трех рисунках.