Уравнение касательной производной. Урок "уравнение касательной к графику функции"

Пример 1. Дана функция f (x ) = 3x 2 + 4x – 5. Напишем уравнение касательной к графику функции f (x ) в точке графика с абсциссой x 0 = 1.

Решение. Производная функции f (x ) существует для любого x R . Найдем ее:

= (3x 2 + 4x – 5)′ = 6x + 4.

Тогда f (x 0) = f (1) = 2; (x 0) = = 10. Уравнение касательной имеет вид:

y = (x 0) (x – x 0) + f (x 0),

y = 10(x – 1) + 2,

y = 10x – 8.

Ответ. y = 10x – 8.

Пример 2. Дана функция f (x ) = x 3 – 3x 2 + 2x + 5. Напишем уравнение касательной к графику функции f (x ), параллельной прямой y = 2x – 11.

Решение. Производная функции f (x ) существует для любого x R . Найдем ее:

= (x 3 – 3x 2 + 2x + 5)′ = 3x 2 – 6x + 2.

Так как касательная к графику функции f (x ) в точке с абсциссой x 0 параллельна прямой y = 2x – 11, то ее угловой коэффициент равен 2, т. е. (x 0) = 2. Найдем эту абсциссу из условия, что 3x – 6x 0 + 2 = 2. Это равенство справедливо лишь при x 0 = 0 и при x 0 = 2. Так как в том и в другом случае f (x 0) = 5, то прямая y = 2x + b касается графика функции или в точке (0; 5), или в точке (2; 5).

В первом случае верно числовое равенство 5 = 2×0 + b , откуда b = 5, а во втором случае верно числовое равенство 5 = 2×2 + b , откуда b = 1.

Итак, существует две касательные y = 2x + 5 и y = 2x + 1 к графику функции f (x ), параллельные прямой y = 2x – 11.

Ответ. y = 2x + 5, y = 2x + 1.

Пример 3. Дана функция f (x ) = x 2 – 6x + 7. Напишем уравнение касательной к графику функции f (x ), проходящей через точку A (2; –5).

Решение. Так как f (2) –5, то точка A не принадлежит графику функции f (x ). Пусть x 0 - абсцисса точки касания.

Производная функции f (x ) существует для любого x R . Найдем ее:

= (x 2 – 6x + 1)′ = 2x – 6.

Тогда f (x 0) = x – 6x 0 + 7; (x 0) = 2x 0 – 6. Уравнение касательной имеет вид:

y = (2x 0 – 6)(x – x 0) + x – 6x + 7,

y = (2x 0 – 6)x – x + 7.

Так как точка A принадлежит касательной, то справедливо числовое равенство

–5 = (2x 0 – 6)×2– x + 7,

откуда x 0 = 0 или x 0 = 4. Это означает, что через точку A можно провести две касательные к графику функции f (x ).

Если x 0 = 0, то уравнение касательной имеет вид y = –6x + 7. Если x 0 = 4, то уравнение касательной имеет вид y = 2x – 9.

Ответ. y = –6x + 7, y = 2x – 9.

Пример 4. Даны функции f (x ) = x 2 – 2x + 2 и g (x ) = –x 2 – 3. Напишем уравнение общей касательной к графикам этих функции.

Решение. Пусть x 1 - абсцисса точки касания искомой прямой с графиком функции f (x ), а x 2 - абсцисса точки касания той же прямой с графиком функции g (x ).

Производная функции f (x ) существует для любого x R . Найдем ее:

= (x 2 – 2x + 2)′ = 2x – 2.

Тогда f (x 1) = x – 2x 1 + 2; (x 1) = 2 x 1 – 2. Уравнение касательной имеет вид:

y = (2x 1 – 2)(x – x 1) + x – 2x 1 + 2,

y = (2x 1 – 2)x – x + 2. (1)

Найдем производную функции g (x ):

= (–x 2 – 3)′ = –2x .

Уравнение касательной к графику функции

П. Романов, Т. Романова,
г. Магнитогорск,
Челябинская обл.

Уравнение касательной к графику функции

Статья опубликована при поддержке Гостиничного комплекса «ИТАКА+». Останавливаясь в городе судостроителей Северодвинске, вы не столкнетесь с проблемой поиска временного жилья. , на сайте гостиничного комплекса «ИТАКА+» http://itakaplus.ru, вы сможете легко и быстро снять квартиру в городе, на любой срок, с посуточной оплатой.

На современном этапе развития образования в качестве одной из основных его задач выступает формирование творчески мыслящей личности. Способность же к творчеству у учащихся может быть развита лишь при условии систематического привлечения их к основам исследовательской деятельности. Фундаментом для применения учащимися своих творческих сил, способностей и дарований являются сформированные полноценные знания и умения. В связи с этим проблема формирования системы базовых знаний и умений по каждой теме школьного курса математики имеет немаловажное значение. При этом полноценные умения должны являться дидактической целью не отдельных задач, а тщательно продуманной их системы. В самом широком смысле под системой понимается совокупность взаимосвязанных взаимодействующих элементов, обладающая целостностью и устойчивой структурой.

Рассмотрим методику обучения учащихся составлению уравнения касательной к графику функции. По существу, все задачи на отыскание уравнения касательной сводятся к необходимости отбора из множества (пучка, семейства) прямых тех из них, которые удовлетворяют определенному требованию – являются касательными к графику некоторой функции. При этом множество прямых, из которого осуществляется отбор, может быть задано двумя способами:

а) точкой, лежащей на плоскости xOy (центральный пучок прямых);
б) угловым коэффициентом (параллельный пучок прямых).

В связи с этим при изучении темы «Касательная к графику функции» с целью вычленения элементов системы нами были выделены два типа задач:

1) задачи на касательную, заданную точкой, через которую она проходит;
2) задачи на касательную, заданную ее угловым коэффициентом.

Обучение решению задач на касательную осуществлялось при помощи алгоритма, предложенного А.Г. Мордковичем . Его принципиальное отличие от уже известных заключается в том, что абсцисса точки касания обозначается буквой a (вместо x0), в связи с чем уравнение касательной приобретает вид

y = f(a) + f "(a)(x – a)

(сравните с y = f(x 0) + f "(x 0)(x – x 0)). Этот методический прием, на наш взгляд, позволяет учащимся быстрее и легче осознать, где в общем уравнении касательной записаны координаты текущей точки, а где – точки касания.

Алгоритм составления уравнения касательной к графику функции y = f(x)

1. Обозначить буквой a абсциссу точки касания.
2. Найти f(a).
3. Найти f "(x) и f "(a).
4. Подставить найденные числа a, f(a), f "(a) в общее уравнение касательной y = f(a) = f "(a)(x – a).

Этот алгоритм может быть составлен на основе самостоятельного выделения учащимися операций и последовательности их выполнения.

Практика показала, что последовательное решение каждой из ключевых задач при помощи алгоритма позволяет формировать умения написания уравнения касательной к графику функции поэтапно, а шаги алгоритма служат опорными пунктами действий. Данный подход соответствует теории поэтапного формирования умственных действий, разработанной П.Я. Гальпериным и Н.Ф. Талызиной .

В первом типе задач были выделены две ключевые задачи:

• касательная проходит через точку, лежащую на кривой (задача 1);
• касательная проходит через точку, не лежащую на кривой (задача 2).

Задача 1. Составьте уравнение касательной к графику функции в точке M(3; – 2).

Решение. Точка M(3; – 2) является точкой касания, так как

1. a = 3 – абсцисса точки касания.
2. f(3) = – 2.
3. f "(x) = x 2 – 4, f "(3) = 5.
y = – 2 + 5(x – 3), y = 5x – 17 – уравнение касательной.

Задача 2. Напишите уравнения всех касательных к графику функции y = – x 2 – 4x + 2, проходящих через точку M(– 3; 6).

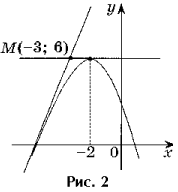Решение. Точка M(– 3; 6) не является точкой касания, так как f(– 3) ­ 6 (рис. 2).

2. f(a) = – a 2 – 4a + 2.
3. f "(x) = – 2x – 4, f "(a) = – 2a – 4.
4. y = – a 2 – 4a + 2 – 2(a + 2)(x – a) – уравнение касательной.

Касательная проходит через точку M(– 3; 6), следовательно, ее координаты удовлетворяют уравнению касательной.

6 = – a 2 – 4a + 2 – 2(a + 2)(– 3 – a),
a 2 + 6a + 8 = 0 ^ a 1 = – 4, a 2 = – 2.

Если a = – 4, то уравнение касательной имеет вид y = 4x + 18.

Если a = – 2, то уравнение касательной имеет вид y = 6.

Во втором типе ключевыми задачами будут следующие:

• касательная параллельна некоторой прямой (задача 3);
• касательная проходит под некоторым углом к данной прямой (задача 4).

Задача 3. Напишите уравнения всех касательных к графику функции y = x 3 – 3x 2 + 3, параллельных прямой y = 9x + 1.

Решение.

1. a – абсцисса точки касания.
2. f(a) = a 3 – 3a 2 + 3.
3. f "(x) = 3x 2 – 6x, f "(a) = 3a 2 – 6a.

Но, с другой стороны, f "(a) = 9 (условие параллельности). Значит, надо решить уравнение 3a 2 – 6a = 9. Его корни a = – 1, a = 3 (рис. 3).

4. 1) a = – 1;
2) f(– 1) = – 1;
3) f "(– 1) = 9;
4) y = – 1 + 9(x + 1);

y = 9x + 8 – уравнение касательной;

1) a = 3;
2) f(3) = 3;
3) f "(3) = 9;
4) y = 3 + 9(x – 3);

y = 9x – 24 – уравнение касательной.

Задача 4. Напишите уравнение касательной к графику функции y = 0,5x 2 – 3x + 1, проходящей под углом 45° к прямой y = 0 (рис. 4).

Решение. Из условия f "(a) = tg 45° найдем a: a – 3 = 1 ^ a = 4.

1. a = 4 – абсцисса точки касания.
2. f(4) = 8 – 12 + 1 = – 3.
3. f "(4) = 4 – 3 = 1.
4. y = – 3 + 1(x – 4).

y = x – 7 – уравнение касательной.

Несложно показать, что решение любой другой задачи сводится к решению одной или нескольких ключевых задач. Рассмотрим в качестве примера следующие две задачи.

1. Напишите уравнения касательных к параболе y = 2x 2 – 5x – 2, если касательные пересекаются под прямым углом и одна из них касается параболы в точке с абсциссой 3 (рис. 5).

Решение. Поскольку дана абсцисса точки касания, то первая часть решения сводится к ключевой задаче 1.

1. a = 3 – абсцисса точки касания одной из сторон прямого угла.
2. f(3) = 1.
3. f "(x) = 4x – 5, f "(3) = 7.
4. y = 1 + 7(x – 3), y = 7x – 20 – уравнение первой касательной.

Пусть a – угол наклона первой касательной. Так как касательные перпендикулярны, то – угол наклона второй касательной. Из уравнения y = 7x – 20 первой касательной имеем tg a = 7. Найдем

Это значит, что угловой коэффициент второй касательной равен .

Дальнейшее решение сводится к ключевой задаче 3.

Пусть B(c; f(c)) есть точка касания второй прямой, тогда

1. – абсцисса второй точки касания.
2.
3.
4.
– уравнение второй касательной.

Примечание. Угловой коэффициент касательной может быть найден проще, если учащимся известно соотношение коэффициентов перпендикулярных прямых k 1 k 2 = – 1.

2. Напишите уравнения всех общих касательных к графикам функций

Решение. Задача сводится к отысканию абсцисс точек касания общих касательных, то есть к решению ключевой задачи 1 в общем виде, составлению системы уравнений и последующему ее решению (рис. 6).

1. Пусть a – абсцисса точки касания, лежащей на графике функции y = x 2 + x + 1.
2. f(a) = a 2 + a + 1.
3. f "(a) = 2a + 1.
4. y = a 2 + a + 1 + (2a + 1)(x – a) = (2a + 1)x + 1 – a 2 .

1. Пусть c – абсцисса точки касания, лежащей на графике функции
2.
3. f "(c) = c.
4.

Так как касательные общие, то

Итак, y = x + 1 и y = – 3x – 3 – общие касательные.

Основная цель рассмотренных задач – подготовить учащихся к самостоятельному распознаванию типа ключевой задачи при решении более сложных задач, требующих определенных исследовательских умений (умения анализировать, сравнивать, обобщать, выдвигать гипотезу и т. д.). К числу таких задач можно отнести любую задачу, в которую ключевая задача входит как составляющая. Рассмотрим в качестве примера задачу (обратную задаче 1) на нахождение функции по семейству ее касательных.

3. При каких b и c прямые y = x и y = – 2x являются касательными к графику функции y = x 2 + bx + c?

Решение.

Пусть t – абсцисса точки касания прямой y = x с параболой y = x 2 + bx + c; p – абсцисса точки касания прямой y = – 2x с параболой y = x 2 + bx + c. Тогда уравнение касательной y = x примет вид y = (2t + b)x + c – t 2 , а уравнение касательной y = – 2x примет вид y = (2p + b)x + c – p 2 .

Составим и решим систему уравнений

Ответ:

Задачи для самостоятельного решения

1. Напишите уравнения касательных, проведенных к графику функции y = 2x 2 – 4x + 3 в точках пересечения графика с прямой y = x + 3.

Ответ: y = – 4x + 3, y = 6x – 9,5.

2. При каких значениях a касательная, проведенная к графику функции y = x 2 – ax в точке графика с абсциссой x 0 = 1, проходит через точку M(2; 3)?

Ответ: a = 0,5.

3. При каких значениях p прямая y = px – 5 касается кривой y = 3x 2 – 4x – 2?

Ответ: p 1 = – 10, p 2 = 2.

4. Найдите все общие точки графика функции y = 3x – x 3 и касательной, проведенной к этому графику через точку P(0; 16).

Ответ: A(2; – 2), B(– 4; 52).

5. Найдите кратчайшее расстояние между параболой y = x 2 + 6x + 10 и прямой

Ответ:

6. На кривой y = x 2 – x + 1 найдите точку, в которой касательная к графику параллельна прямой y – 3x + 1 = 0.

Ответ: M(2; 3).

7. Напишите уравнение касательной к графику функции y = x 2 + 2x – | 4x |, которая касается его в двух точках. Сделайте чертеж.

Ответ: y = 2x – 4.

8. Докажите, что прямая y = 2x – 1 не пересекает кривую y = x 4 + 3x 2 + 2x. Найдите расстояние между их ближайшими точками.

Ответ:

9. На параболе y = x 2 взяты две точки с абсциссами x 1 = 1, x 2 = 3. Через эти точки проведена секущая. В какой точке параболы касательная к ней будет параллельна проведенной секущей? Напишите уравнения секущей и касательной.

Ответ: y = 4x – 3 – уравнение секущей; y = 4x – 4 – уравнение касательной.

10. Найдите угол q между касательными к графику функции y = x 3 – 4x 2 + 3x + 1, проведенными в точках с абсциссами 0 и 1.

Ответ: q = 45°.

11. В каких точках касательная к графику функции образует с осью Ox угол в 135°?

Ответ: A(0; – 1), B(4; 3).

12. В точке A(1; 8) к кривой проведена касательная. Найдите длину отрезка касательной, заключенного между осями координат.

Ответ:

13. Напишите уравнение всех общих касательных к графикам функций y = x 2 – x + 1 и y = 2x 2 – x + 0,5.

Ответ: y = – 3x и y = x.

14. Найдите расстояние между касательными к графику функции параллельными оси абсцисс.

Ответ:

15. Определите, под какими углами парабола y = x 2 + 2x – 8 пересекает ось абсцисс.

Ответ: q 1 = arctg 6, q 2 = arctg (– 6).

16. На графике функции найдите все точки, касательная в каждой из которых к этому графику пересекает положительные полуоси координат, отсекая от них равные отрезки.

Ответ: A(– 3; 11).

17. Прямая y = 2x + 7 и парабола y = x 2 – 1 пересекаются в точках M и N. Найдите точку K пересечения прямых, касающихся параболы в точках M и N.

Ответ: K(1; – 9).

18. При каких значениях b прямая y = 9x + b является касательной к графику функции y = x 3 – 3x + 15?

Ответ: – 1; 31.

19. При каких значениях k прямая y = kx – 10 имеет только одну общую точку с графиком функции y = 2x 2 + 3x – 2? Для найденных значений k определите координаты точки.

Ответ: k 1 = – 5, A(– 2; 0); k 2 = 11, B(2; 12).

20. При каких значениях b касательная, проведенная к графику функции y = bx 3 – 2x 2 – 4 в точке с абсциссой x 0 = 2, проходит через точку M(1; 8)?

Ответ: b = – 3.

21. Парабола с вершиной на оси Ox касается прямой, проходящей через точки A(1; 2) и B(2; 4), в точке B. Найдите уравнение параболы.

Ответ:

22. При каком значении коэффициента k парабола y = x 2 + kx + 1 касается оси Ox?

Ответ: k = д 2.

23. Найдите углы между прямой y = x + 2 и кривой y = 2x 2 + 4x – 3.

29. Найдите расстояние между касательными к графику функции образующими с положительным направлением оси Ox угол 45°.

Ответ:

30. Найдите геометрическое место вершин всех парабол вида y = x 2 + ax + b, касающихся прямой y = 4x – 1.

Ответ: прямая y = 4x + 3.

Литература

1. Звавич Л.И., Шляпочник Л.Я., Чинкина М.В. Алгебра и начала анализа: 3600 задач для школьников и поступающих в вузы. – М., Дрофа, 1999.
2. Мордкович А. Семинар четвертый для молодых учителей. Тема «Приложения производной». – М., «Математика», № 21/94.
3. Формирование знаний и умений на основе теории поэтапного усвоения умственных действий. / Под ред. П.Я. Гальперина, Н.Ф. Талызиной. – М., МГУ, 1968.

Рассмотрим следующий рисунок:

На нем изображена некоторая функция y = f(x), которая дифференцируема в точке a. Отмечена точка М с координатами (а; f(a)). Через произвольную точку Р(a + ∆x; f(a + ∆x)) графика проведена секущая МР.

Если теперь точку Р сдвигать по графику к точке М, то прямая МР будет поворачиваться вокруг точки М. При этом ∆х будет стремиться к нулю. Отсюда можно сформулировать определение касательной к графику функции.

Касательная к графику функции

Касательная к графику функции есть предельное положение секущей при стремлении приращения аргумента к нулю. Следует понимать, что существование производной функции f в точке х0, означает, что в этой точке графика существует касательная к нему.

При этом угловой коэффициент касательной будет равен производной этой функции в этой точке f’(x0). В этом заключается геометрический смысл производной. Касательная к графику дифференцируемой в точке х0 функции f - это некоторая прямая, проходящая через точку (x0;f(x0)) и имеющая угловой коэффициент f’(x0).

Уравнение касательной

Попытаемся получить уравнение касательной к графику некоторой функции f в точке А(x0; f(x0)). Уравнение прямой с угловым коэффициентом k имеет следующий вид:

Так как у нас угловой коэффициент равен производной f’(x0) , то уравнение примет следующий вид: y = f’(x0) *x + b.

Теперь вычислим значение b. Для этого используем тот факт, что функция проходит через точку А.

f(x0) = f’(x0)*x0 + b, отсюда выражаем b и получим b = f(x0) - f’(x0)*x0.

Подставляем полученное значение в уравнение касательной:

y = f’(x0)*x + b = f’(x0)*x + f(x0) - f’(x0)*x0 = f(x0) + f’(x0)*(x - x0).

y = f(x0) + f’(x0)*(x - x0).

Рассмотрим следующий пример: найти уравнение касательной к графику функции f(x) = x 3 - 2*x 2 + 1 в точке х = 2.

2. f(x0) = f(2) = 2 2 - 2*2 2 + 1 = 1.

3. f’(x) = 3*x 2 - 4*x.

4. f’(x0) = f’(2) = 3*2 2 - 4*2 = 4.

5. Подставим полученные значения в формулу касательной, получим: y = 1 + 4*(x - 2). Раскрыв скобки и приведя подобные слагаемые получим: y = 4*x - 7.

Ответ: y = 4*x - 7.

Общая схема составления уравнения касательной к графику функции y = f(x):

1. Определить х0.

2. Вычислить f(x0).

3. Вычислить f’(x)

У = f(х) и если в этой точке к графику функции можно провести касательную, не перпендикулярную к оси абсцисс, то угловой коэффициент касательной равен f"(а). Мы этим уже несколько раз пользовались. Например, в § 33 было установлено, что график функции у = sin х(синусоида) в начале координат образует с осью абсцисс угол 45° (точнее, касательная к графику в начале координат составляет с положительным направлением оси х угол 45°), а в примере 5 § 33 были найдены точки на графике заданной функции , в которых касательная параллельна оси абсцисс. В примере 2 § 33 было составлено уравнение касательной к графику функции у = х 2 в точке х = 1 (точнее, в точке (1; 1), но чаще указывают только значение абсциссы, полагая, что если значение абсциссы известно, то значение ординаты можно найти из уравнения у = f(х)). В этом параграфе мы выработаем алгоритм составления уравнения касательной.к графику любой функции.

Пусть даны функция у = f(х) и точка М (а; f(а)), а также известно, что существует f"(а). Составим уравнение касательной к графику заданной функции в заданной точке. Это уравнение, как уравнение любой прямой, не параллельной оси ординат, имеет вид у = кх+m, поэтому задача состоит в отыскании значений коэффициентов к и m.

С угловым коэффициентом к проблем нет: мы знаем, что к = f"(а). Для вычисления значения т воспользуемся тем, что искомая прямая проходит через точку М(а; f (а)). Это значит, что, если подставить координаты точки М в уравнение прямой, получим верное равенство: f(а) = ка+m, откуда находим, что m = f(а) - ка.
Осталось подставить найденные значения коэффициентов кит в уравнение прямой:

Нами получено уравнение касательной к графику функции у = f(х) в точке х=а.
Если, скажем,
Подставив в уравнение (1) найденные значения а = 1, f(а) = 1 f"(а) = 2, получим: у = 1+2(х-f), т.е. у = 2х-1.
Сравните этот результат с тем, что был получен в примере 2 из § 33. Естественно, получилось то же самое.
Составим уравнение касательной к графику функции у = tg х в начале координат. Имеем: значит, соs х f"(0) = 1. Подставив в уравнение (1) найденные значения а= 0, f(а)= 0, f"(а) = 1, получим: у=х.
Именно поэтому мы и провели тангенсоиду в § 15 (см. рис. 62) через начало координат под углом 45° к оси абсцисс.
Решая эти достаточно простые примеры, мы фактически пользовались определенным алгоритмом, который заложен в формуле (1). Сделаем этот алгоритм явным.

АЛГОРИТМ СОСТАВЛЕНИЯ УРАВНЕНИЯ КАСАТЕЛЬНОЙ К ГРАФИКУ ФУНКЦИИ у = f(x)

1) Обозначить абсциссу точки касания буквой а.
2) Вычислить 1 (а).
3) Найти f"(х) и вычислить f"(а).
4) Подставить найденные числа а, f(а), (а) в формулу (1).

Пример 1. Составить уравнение касательной к графику функции в точке х = 1.
Воспользуемся алгоритмом, учитывая, что в данном примере

На рис. 126 изображена гипербола , построена прямая у= 2-х.
Чертеж подтверждает приведенные выкладки: действительно, прямая у = 2-х касается гиперболы в точке(1; 1).

Ответ: у =2- х.
Пример 2. К графику функции провести касательную так, чтобы она была параллельна прямой у =4х - 5.
Уточним формулировку задачи. Требование «провести касательную» обычно означает «составить уравнение касательной». Это логично, ибо если человек смог составить уравнение касательной, то вряд ли он будет испытывать затруднения с построением на координатной плоскости прямой по ее уравнению.
Воспользуемся алгоритмом составления уравнения касательной, учитывая, что в данном примере Но в отличие от предыдущего примера здесь имеется неясность: не указана явно абсцисса точки касания.
Начнем рассуждать так. Искомая касательная должна быть параллельна прямой у = 4х-5. Две прямые параллельны тогда и только тогда, когда равны их угловые коэффициенты. Значит, угловой коэффициент касательной должен быть равен угловому коэффициенту заданной прямой: Таким образом, значение а мы можем найти из уравнения f"(а)= 4.
Имеем:
Из уравнения Значит, имеются две касательные, удовлетворяющие условию задачи: одна в точке с абсциссой 2, другая в точке с абсциссой -2.
Теперь можно действовать по алгоритму.

Пример 3. Из точки (0; 1) провести касательную к графику функции
Воспользуемся алгоритмом составления уравнения касательной, учитывая, что в данном примере Заметим, что и здесь, как в примере 2, не указана явно абсцисса точки касания. Тем не менее действуем по алгоритму.

По условию касательная проходит через точку (0; 1). Подставив в уравнение (2) значения х = 0, у = 1, получим:
Как видите, в этом примере только на четвертом шаге алгоритма нам удалось найти абсциссу точки касания. Подставив значение а =4 в уравнение (2), получим:

На рис. 127 представлена геометрическая иллюстрация рассмотренного примера: построен график функции

В § 32 мы отметили, что для функции у = f(х), имеющей производную в фиксированной точке х, справедливо приближенное равенство:

Для удобства дальнейших рассуждений изменим обозначения: вместо х будем писать а, вместо будем писать х и соответственно вместо будем писать х-а. Тогда написанное выше приближенное равенство примет вид:

А теперь взгляните на рис. 128. К графику функции у = f(х) проведена касательная в точке М (а; f (а)). Отмечена точка х на оси абсцисс близко от а. Ясно, что f(х) - ордината графика функции в указанной точке х. А что такое f(а) + f"(а) (х-а)? Это ордината касательной, соответствующая той же точке х - см. формулу (1). В чем же смысл приближенного равенства (3)? В том, что для вычисления приближенного значения функции берут значение ординаты касательной.

Пример 4. Найти приближенное значение числового выражения 1,02 7 .
Речь идет об отыскании значения функции у = х 7 в точке х = 1,02. Воспользуемся формулой (3), учтя, что в данном примере
В итоге получаем:

Если мы воспользуемся калькулятором, то получим: 1,02 7 = 1,148685667...
Как видите, точность приближения вполне приемлема.
Ответ: 1,02 7 =1,14.

А.Г. Мордкович Алгебра 10 класс

Календарно-тематическое планирование по математике, видео по математике онлайн , Математика в школе скачать

Пусть дана функция f , которая в некоторой точке x 0 имеет конечную производную f (x 0). Тогда прямая, проходящая через точку (x 0 ; f (x 0)), имеющая угловой коэффициент f ’(x 0), называется касательной.

А что будет, если производная в точке x 0 не существует? Возможны два варианта:

1. Касательная к графику тоже не существует. Классический пример - функция y = |x | в точке (0; 0).
2. Касательная становится вертикальной. Это верно, к примеру, для функции y = arcsin x в точке (1; π /2).

Уравнение касательной

Всякая невертикальная прямая задается уравнением вида y = kx + b , где k - угловой коэффициент. Касательная - не исключение, и чтобы составить ее уравнение в некоторой точке x 0 , достаточно знать значение функции и производной в этой точке.

Итак, пусть дана функция y = f (x ), которая имеет производную y = f ’(x ) на отрезке . Тогда в любой точке x 0 ∈ (a ; b ) к графику этой функции можно провести касательную, которая задается уравнением:

y = f ’(x 0) · (x − x 0) + f (x 0)

Здесь f ’(x 0) - значение производной в точке x 0 , а f (x 0) - значение самой функции.

Задача. Дана функция y = x 3 . Составить уравнение касательной к графику этой функции в точке x 0 = 2.

Уравнение касательной: y = f ’(x 0) · (x − x 0) + f (x 0). Точка x 0 = 2 нам дана, а вот значения f (x 0) и f ’(x 0) придется вычислять.

Для начала найдем значение функции. Тут все легко: f (x 0) = f (2) = 2 3 = 8;
Теперь найдем производную: f ’(x ) = (x 3)’ = 3x 2 ;
Подставляем в производную x 0 = 2: f ’(x 0) = f ’(2) = 3 · 2 2 = 12;
Итого получаем: y = 12 · (x − 2) + 8 = 12x − 24 + 8 = 12x − 16.
Это и есть уравнение касательной.

Задача. Составить уравнение касательной к графику функции f (x ) = 2sin x + 5 в точке x 0 = π /2.

В этот раз не будем подробно расписывать каждое действие - укажем лишь ключевые шаги. Имеем:

f (x 0) = f (π /2) = 2sin (π /2) + 5 = 2 + 5 = 7;
f ’(x ) = (2sin x + 5)’ = 2cos x ;
f ’(x 0) = f ’(π /2) = 2cos (π /2) = 0;

Уравнение касательной:

y = 0 · (x − π /2) + 7 ⇒ y = 7

В последнем случае прямая оказалась горизонтальной, т.к. ее угловой коэффициент k = 0. Ничего страшного в этом нет - просто мы наткнулись на точку экстремума.