Поверхностный интеграл первого и второго рода. Поверхностные интегралы

Рассмотрим интегралы от функций, заданных на поверхностях, так называемые поверхностные интегралы.Теория поверхностных интегралов во многом аналогична теории криволинейных интегралов. Различают поверхностные интегралы первого и

второго рода.

4.1. Поверхностные интегралы первого типа. Пусть функция f (x , y , z )

определена на кусочно-гладкой поверхностиS , ограниченной кусочногладким контуром (рис. 4.1). Разобьем

соответственно ∆ s 1 , ∆ s 2 ..., ∆ s n . Взяв в пределах каждой частиS i , i = 1, n произвольную точкуM i (x i , y i , z i ) , вычислим значение функции в ней и составим следующую сумму:

если он существует и не зависит ни от способа разбиения поверхности на частичные, ни от выбора точек, то он называется поверхностным интегралом первого типа (по площади поверхности) от функции

Поверхностный интеграл первого типа представляет собой обобщение двойного интеграла, поэтому условия существования двойного интеграла и его свойства легко переносятся на поверхностный интеграл первого типа.

Вычисление поверхностных интегралов первого типа сводится к вычислению двойных интегралов: исходя из уравнения поверхности S ,

подынтегральное выраражение преобразуется к двум переменным, областью изменения которых будет проекция поверхности S на соответствующую этим переменным координатную плоскость.

Пусть поверхность S задана уравнениемz = z (x , y ) иz (x , y ) непрерывна вместе со своими частными производнымиz ′ x , z ′ y в замкнутой областиS xy , являющейся проекцией поверхностиS на координатную плоскостьxOy , тогда

Эта формула выражает поверхностный интеграл первого типа через двойной интеграл по проекции поверхности S на координатную плоскостьxOy .

Аналогично вычисляются поверхностные интегралы первого типа по поверхности S через двойные интегралы по ее проекциям на

С помощью поверхностных интегралов первого типа можно вычислить площадь поверхности, а также массу, статические моменты, моменты инерции и координаты центра масс для материальных поверхностей с известной поверхностной плотностью распределения масс.

Пример 4.1. Вычислить

∫∫ 1 + 4 x 2 + 4 y 2 ds , гдеS - часть парабо-

лоида вращения z = 1 − x 2 − y 2 , отсеченного плоскостьюz = 0 .

Решение. Спроектируем поверхность

S на плоскостьxOy .

Проекция S xy - есть круг, ограниченный окружностьюx 2 + y 2 = 1 (рис.

4.2). Заданный поверхностный интеграл будем вычислять по формуле (4.2), для чего найдем z ′ x = − 2 x , z ′ y = − 2 y . Тогда, совершая в двойном

4.2. Двусторонние поверхности. Поверхность S называется

двусторонней , если обход по любому замкнутому контуру, лежащему на поверхностиS и не пересекающему ее границ, при возвращении в исходную точку не меняет направление нормали к поверхности. В противном случае поверхность называется односторонней. Примеры двусторонних поверхностей: плоскость, сфера и любая поверхность, заданная уравнениемz = z (x , y ) , гдеz = z (x , y ) ,z ′ x (x , y ) ,z ′ y (x , y ) - непрерывны в некоторой областиG . Примером односторонней поверхности является лист Мёбиуса.

4.3. Поверхностный интеграл второго типа. Пусть S - гладкая поверхность, заданная уравнением z = z (x , y ) и функция f (x , y , z )

определена в точках поверхности S.

Выберем одну из сторон поверхности, то есть одно из двух возможных направлений нормали в точках поверхности (этим мы сориентировали поверхность). Если нормали составляют острые углы с

осью Oz , то будем говорить о верхней стороне поверхности(о положительном направлении нормали), а если нормали составляют – тупые углыс осью Oz , то говорим о нижней стороне поверхности (об отрицательном направлении нормали).

Разобьем поверхность S произвольным образом наn частейS 1 , S 2 ..., S n , и через(S xy ) i обозначим проекцию i -ой части поверхности

на плоскость xOy . В пределах каждой частичной поверхностиS i , i = 1, n выберем произвольную точкуM i (x i , y i , z i ) , вычислим значение функции

в ней и составим сумму

σ n= ∑ f (x i, y i, z i) ∆ s i, i = 1

где ∆ s i - площадь(S xy ) i , взятая со знаком плюс, если выбрана верхняя сторона поверхностиS и со знаком минус, если выбрана нижняя сторона

поверхности S . Эта суммаσ n называетсяинтегральной суммой для функцииf (x , y , z ) .

Конечный предел I интегральной суммы, при стремлении к нулю наибольшегоλ из всех диаметров проекций(S xy ) i , если он существует и

не зависит ни от способа разбиения поверхности S , ни от выбора точек

M i (x i , y i , z i ) , то этот предел называетсяповерхностным интегралом второго типа от функции f (x , y , z ) по выбранной стороне поверхности по переменным x и y и обозначается∫∫ f (x , y , z ) dxdy . Таким образом, по

определению

поверхности S по переменнымx иy .

Аналогично можно определить поверхностные интегралы второго типа по выбранной стороне поверхности S по переменнымy иz , по переменнымx иz :

Пусть P (x , y , z ), Q (x , y , z ), R (x , y , z ) функции, интегрируемые по

поверхности S по переменнымy иz ,x иz , x иy соответственно. Сумма интегралов

Так как поверхность S считаем двусторонней и интеграл распространяется на определенную ее сторону, топри изменении стороны поверхности интегрирования поверхностный интеграл второго типа меняет знак на противоположный – в этом его отличие от поверхностного интеграла первого типа.

Вычисление поверхностных интегралов второго типа сводится к вычислению двойных интегралов.

Пусть ориентированная (выберем верхнюю сторону) гладкая поверхность S задана уравнениемz = z (x , y ) , гдеz (x , y ) непрерывна в

замкнутой области S xy - проекции поверхностиS на плоскостьxOy ; функцияf (x , y , z ) непрерывна наS . Тогда справедлива формула

плоскости yOz иxOz .

Для вычисления интеграла общего вида (4.6) используются формулы (4.7)–(4.9), если поверхностьS однозначно проектируется на все

координатные плоскости. В более сложных случаях поверхность S разбивают на части, обладающие указанными свойствами, а общий интеграл представляют в виде интегралов по этим частям.

Пример 4.2.Вычислить

∫∫ (y 2 + z 2 ) dxdy , гдеS верхняя сторона

4.4. Формула Остроградского. Формула Остроградского устанавливает связь между поверхностным интегралом по замкнутой поверхности и тройным интегралом по пространственной области, ограниченной этой поверхностью .

Пусть V - правильная замкнутая область, ограниченная поверхностьюS , и пусть функцииP (x , y , z ), Q (x , y , z ), R (x , y , z )

непрерывны вместе со своими частными производными первого порядка в данной области. Тогда имеет место следующая формула:

называемая формулой Остроградского1 .

С помощью формулы Остроградского удобно вычислять поверхностные интегралы по замкнутым поверхностям.

Пример 4.4. С помощью формулы Остроградского вычислить

Замечание 4.1. Связь между поверхностными интегралами первого и второго типов аналогична связи криволинейных интегралов:

∫∫ f( x, y, z) dxdy= ∫∫ f( x, y, z) cos α ds,

∫∫ f( x, y, z) dydz= ∫∫ f( x, y, z) cos β ds,

∫∫ f( x, y, z) dxdz= ∫∫ f( x, y, z) cos γ ds,

где cos α ,cos β ,cos γ - направляющие косинусы нормали, отвечающей

Понятие о двукратном интеграле по плоской области без труда обобщается на случай интегрирования по поверхности. Пусть (S) - поверхность (замкнутая или незамкнутая) и непрерывная функция точки на этой поверхности. Разбиваем (S) на частей

и пусть площади этих частей и какие-либо точки, находящиеся на этих частях. Составляем сумму произведений

Предел этой суммы при беспредельном возрастании числа делений и беспредельном уменьшении каждой из частей называется интегралом от функции по поверхности

Положим, что прямые, параллельные оси Z, пересекают поверхность только в одной точке (рис. 48) и пусть проекция (S) на плоскость ХОY. Пользуясь формулой (26), устанавливающей связь между элементарной площадью поверхности (S) и соответствующей площадью ее проекции , сможем привести интеграл по поверхности (S) к интегралу по плоской области :

при этом считается, что отличен от нуля и что значение функции в точке N области совпадает со значением заданной на поверхности функции в той точке М, проекция которой совпадает с . Если уравнение поверхности (S) задано в явной форме (22) и функция выражена через координаты , то при интегрировании по достаточно подставить в выражение функции . Знаменатель в правой части (29) определится по третьей из формул (24).

Отметим, что интегралы по поверхности, очевидно, обладают всеми свойствами двойного интеграла, указанными в , в частности для них имеет место теорема о среднем.

Докажем теперь одну из основных в теории кратных интегралов формул - формулу Остроградского, устанавливающую связь между трехкратным интегралом по объему и интегралом по поверхности (S), ограничивающей этот объем. Будем считать, как и в что прямые, параллельные оси Z, пересекают (S) не более чем в двух

точках. Сохраним те же обозначения, что и на рис. 40 . Введем еще в рассмотрение направление нормали к (S), причем будем считать, что направлено вовне объема (V) (внешняя нормаль) (рис. 50). Это направление образует на верхней части поверхности (И) острый угол с осью OZ, а на нижней части (I) - тупой угол. Поэтому на нижней части Отметим, что на линии касания поверхности (5) с проектирующим цилиндром (рис. 50). Формула (26) дает

Пусть вместе с производной - непрерывна в области вплоть до (S). Рассмотрим тройной интеграл по от функции Пользуясь формулой (16), будем иметь

Но интеграл от производной равен разности значений первообразной функции при верхнем и нижнем пределах:

Заменяя на по формулам (30), мы сведем интегрирование к интегрированию по (S), причем в первом интеграле, содержащем переменную ординату части (И) поверхности (S), придется пользоваться первой из формул (30), и получится интеграл по (II), во втором интеграле, содержащем придется пользоваться второй из формул (30), и получится интеграл по (I):

Значки у z можно уже не писать, так как указано, по какой именно части поверхности производится интегрирование. В правой части стоит сумма интегралов по частям (II) и (I), т. е. интеграл по всей

поверхности (S):

Если - функции, обладающие свойствами функции R, то, принимая во внимание, что

можем на основании (31) написать формулу интегрирования по частям:

Совершенно так же, взяв две другие функции мы могли бы доказать

Складывая почленно полученные три формулы, придем к формуле Остроградского

Аналогично (31,) записываются формулы интегрирования по частям для производных по х и у.

Мы не пишем здесь для краткости аргументов х, у, z у функций Р, Q и но надо помнить, что это суть функции, определенные в объеме и непрерывные со своими производными.

В следующей главе мы приведем большое число примеров применения формулы Остроградского.

Величины суть функции, определенные на поверхности (S). Мы их считали непрерывными. Можно сделать более общее предположение, а именно считать, что (S) разбивается на конечное число кусков, на каждом из которых указанные функции непрерывны. Это будет, например, иметь место, если (S) есть многогранник.

При выводе формулы (31) мы предполагали, что прямые, параллельные оси , пересекают поверхность (S) области не более чем в двух точках. Нетрудно обобщить эту формулу и на области более общего вида. Заметим прежде всего, что если поверхность (S), кроме верхней части (II) и нижней части (I), имеет цилиндрическую боковую часть с образующими, параллельными оси , то на этой боковой части и добавление этой части к правой части формулы (31) не меняет величины интеграла по поверхности, так что все доказательство формулы остается справедливым. В более общем случае достаточно при помощи цилиндрических поверхностей с образующими, параллельными оси , разбить на конечное число частей, удовлетворяющих предыдущим условиям, и применить к каждой части формулу (31). Складывая полученные таким образом формулы, будем иметь в левой части тройной интеграл по всему объему . В правой части будем иметь сумму интегралов по всем поверхностям тех частей, на которые мы разбили (v). Интегралы по приведенным вспомогательным цилиндрическим поверхностям, как указано выше, равны нулю. Таким образом в результате сложения в правой части мы будем иметь интеграл по поверхности (S) первоначального объема . Итак, формула (31) оказывается справедливой и для областей более общего вида.

Пример 3.3. Вычислить работу векторного поля

a = 2x 2 yi – xy 2 j

от начала координат O до точки A(1;1), если движение происходит вдоль: а) отрезка прямой ; б) дуги параболы ; в) ломаной OBA, где B(1;0) (см. рис. 3.1).

Решение . а) Уравнение прямой OA имеет вид y=x . Пусть x=t , тогда уравнение прямой в параметрическом виде примет вид:

x=t, y=t,

причем при движении от A до B параметр t будет меняться от 0 до 1. Тогда совершенная работа будет равна

б) Пусть x=t 2 , y=t , тогда

x=t 2 , y=t, 0£t £1.

.

в) Уравнение прямой (OB) имеет вид y =0 (0£x £1); уравнение прямой (BA) имеет вид x =1 (0£y £1). Тогда

, .

В результате, получаем,

.

Замечание . Если в случае двухмерных полей уравнение линии описывается уравнением y =y (x ), а переменная x изменяется от a до b , то криволинейный интеграл 2-го будет вычисляться по формуле:

. (3.9)

Предыдущий пример можно было бы решить и при помощи этой формулы, не вводя параметр t .

Пример 3.4. Вычислить интеграл

,

где L – дуга параболы y=x 2 +1 от точки A(0;1) до точки B(2;5).

Решение . Сделаем чертеж (см. рис.3.2). Из уравнения параболы получаем y"=2x . Поскольку на дуге параболы AB переменная x изменяется от 0 до 2, то криволинейный интеграл, в соответствии с формулой (3.9), примет вид

4. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ

4.1. Поверхностные интегралы первого рода

Поверхностный интеграл 1-го рода является обобщением двойного интеграла и вводится аналогичным образом. Рассмотрим некоторую поверхность S , гладкую или кусочно-гладкую, и предположим, что функция f(x,y,z ) определена и ограничена на этой поверхности. Разобьем эту поверхность на n произвольных частей. Площадь каждого участка обозначим через Ds i . На каждом участке выберем какую-либо точку с координатами (x i ,y i ,z i ) и вычислим значение функции в каждой такой точке. После этого составим интегральную сумму:

.

Если существует предел интегральных сумм при n ®¥ (при этом max Ds i ®0), т.е. такой предел не зависит ни от способа разбиения, ни от выбора средних точек, то такой предел называется поверхностным интегралом первого рода :

. (4.1)

Если функция f(x,y,z ) непрерывна на поверхности S , то предел (4.1) существует.

Если подынтегральная функция f(x,y,z )º1, то поверхностный интеграл 1-го рода равен площади поверхности S :

. (4.2)

Допустим, что введена декартова система координат, и любая прямая, параллельная оси Oz, может пересекать поверхность S лишь в одной точке. Тогда уравнение поверхности S можно записать в виде

z = z (x,y )

и она однозначно проецируется на плоскость xOy . В результате поверхностный интеграл 1-го рода можно выразить через двойной интеграл

. (4.3)

Пример 4.1. Вычислить интеграл

,

где S – часть конической поверхности z 2 =x 2 +y 2 , 0£z £1.

Решение. Имеем

Тогда искомый интеграл преобразуется в двойной интеграл

где S xy – круг x 2 +y 2 £1. Поэтому

.

4.2. Поверхностные интегралы второго рода

Пусть в некоторой области задано векторное поле

a = a x i + a y j + a z k

и какая-либо двухсторонняя поверхность S . Разобьем поверхность каким-либо способом на элементарные площадки DS i . На каждой площадке выберем произвольную точку P i и составим интегральную сумму:

, (4.4)

где n (P i ) – вектор нормали к заданной поверхности в точке P i . Если существует предел такой суммы при DS i ®0, то этот предел называется поверхностным интегралом 2-го рода (или потоком векторного поля a через поверхность S ) и обозначается символом

или ,

где ds =n ds .

Поскольку единичный вектор нормали имеет своими координатами направляющиеся косинусы n ={cosa, cosb, cosg}. то

Таким образом, вычисление поверхностных интегралов 2-го рода можно свести к вычислению поверхностных интегралов 1-го рода. Однако, что в отличие от поверхностных интегралов 1-го рода интегралы 2-го рода зависят от выбора стороны поверхности. Переход к другой стороне поверхности меняет направление нормали к поверхности, а соответственно и знак интеграла .

Рассмотрим интеграл

.

Пусть уравнение поверхности имеет вид z =j(x,y ) и положительной стороной этой поверхности будем считать ту, нормаль которой образует с осью Oz острый угол. Тогда

cosgds = dxdy.

Поэтому рассматриваемый интеграл можно записать в виде

.

Заменяя z на j(x,y ), придем к двойному интегралу

,

где S xy – проекция поверхности S на плоскость xOy .

На случаи, когда интегрирование происходит не по отрезку кривой, а по ограниченной поверхности. Как и криволинейные интегралы, поверхностные интегралы бывают первого рода и второго рода.

Поверхностный интеграл первого рода записывается в виде

где f (M ) = f (x,y,z ) – функция трёх переменных, а поверхность σ - область интегрирования этой функции. Если f (x,y,z ) равна единице, то поверхностный интеграл равен площади поверхности.

Представьте себе довольно большой подсолнух с очень-очень маленькими семечками. Тогда по сумме поверхностей очень-очень маленьких семечек, расположенных на поверхности подсолнуха, можно вычислить поверхность подсолнуха - таким может быть упрощённое толкование поверхностного интеграла. Почему так?

Давайте перейдём к более формальному определению поверхностного интеграла. Поверхность σ разбита на n частей с площадями Δσ 1 , Δσ 2 , ..., Δσ n . Если выбрать на каждой частичной поверхности (семечке) произвольную точку M i с координатами (ζ i , η i , ς i ,) , то можно составить сумму

Эта сумма называется интегральной суммой для функции f (M ) по поверхности σ . Теперь будем максимально увеличивать число таких маленьких частей, а наибольший диаметр Δσ i - наоборот, уменьшать. Если интегральная сумма при стремлении наибольшего из диаметров частей к нулю (то есть, как мы уже отмечали, все части очень маленькие) имеет предел, то этот предел и называется поверхностным интегралом первого рода от функции f (M ) по поверхности σ .

Вычисление поверхностного интеграла первого рода

Пусть поверхность σ задана уравнением z = z (x , y ) , её проекцией на плоскость xOy является область D xy , при этом функция z = z (x , y ) и её частные производные и непрерывны в области D xy .

Пример 1.

где σ - часть плоскости в первом октанте.

Решение. Чертёж:

Из уравнения плоскости получаем выражение "зет": .

Тогда частные производные: , и

.

Поверхность σ является изображённым на чертеже треугольником ABC , а его проекцией на плоскость xOy - треугольником AOB , который ограничен прямыми x = 0 , y = 0 и 3x + y = 6 . От поверхностного интеграла перейдём к двойному интегралу и решим его:

.

Понятие поверхностного интеграла второго рода

Прежде чем перейти к определению поверхностного интеграла второго рода, требуется познакомиться с понятиями стороны поверхностей и ориентированных поверхностей.

Пусть в пространстве дана гладкая поверхность σ . На этой поверхности выберем произвольную точку M и проведём через неё вектор нормали к поверхности. Через точку M проведём также на поверхности σ произвольный контур, не имеющий общих точек с границей поверхности σ . Точку M вместе с вектором нормали будем перемещать по контуру так, чтобы вектор нормали постоянно был перпендикулярен поверхности σ . По возвращении точки M в начальное положение возможны два случая: направление вектора нормали сохранится или же поменяется на противоположное.

Если направление вектора нормали не поменяется, то поверхность σ называется двусторонней. Если же при обходе контура направление вектора нормали поменяется на противоположное, то поверхность называется односторонней. Двусторонние поверхности называются ориентированными поверхностями, односторонние - неориентированными поверхностями.

Пример односторонней поверхности - лист Мёбиуса (на рисунке выше), который можно сделать из полоски бумаги, одна сторона которой повёрнута на 180 градусов, и затем концы склеены. И вот что здесь важно: для односторонней поверхности понятие поверхностного интеграла второго рода не вводится .

Так что будем рассматривать только двусторонние поверхности. Примеры двусторонних поверхностей - плоскости, сфера, эллипсоил, параболоид.

Положительную сторону двустороней поверхности определяет направление вектора нормали. Противоположная сторона поверхности называется отрицательной. Положительной стороной поверхности называется её верхняя сторона. Если единичные векторы нормали составляют острые углы с осью Oz , то выбрана верхняя сторона поверхности z = z (x , y ) , если углы тупые, то нижняя сторона поверхности.

Как и в случае поверхностного интеграла первого рода, поверхность можно разбить на n частей. При формулировке понятия поверхностного интеграла первого рода в интегральной сумме присутствовали площади каждой из частей, на которые умножаются значения функции f (M i ) . В случае поверхностного интеграла второго рода берутся площади не самих частей, а площади их проекций на координатные плоскости . А функцию трёх переменных для отличия от интеграла первого рода обозначим R (x ,y ,z ) . Тогда интегральная сумма запишется так:

,

где Δs i - площади упомянутых проекций частей стороны поверхности на координатную ось (пока будем считать, что на ось xOy ).

При таких соглашениях и обозначениях определение поверхностного интеграла второго рода аналогично определению интеграла первого рода. А именно: поверхностным интегралом второго рода называется предел данной интегральной суммы при стремлении к нулю наибольшего из диаметров частей рассматриваемой поверхности.

Записывается он так:

.

В данном случае функция R (x ,y ,z ) интегрируема по переменным x и y , так как части поверхности проецировались на плоскость xOy .

Аналогично можно записать и два других поверхностных интеграла второго рода:

(функция P (x ,y ,z ) интегрируема по переменным y и z yOz ),

(функция Q (x ,y ,z ) интегрируема по переменным z и x , так как части поверхности проецируются на плоскость zOx ).

Сумма этих интегралов

называется общим поверхностным интегралом второго рода и обозначается

Вычисление поверхностного интеграла второго рода

Поверхностный интеграл второго рода вычисляется путём разложения общего поверхностного интеграла второго рода на сумму поверхностных интегралов (см. окончание предыдущего параграфа) и сведением каждого из них к двойному интегралу.

Рассмотрим подробно вычисление интеграла

.

Пусть поверхность σ задана уравнением z = z (x , y ) . Положительную сторону поверхности обозначим , отрицателную , а проекцию на плоскость xOy - D xy .

Таким образом, получаем формулу для вычисления поверхностного интеграла второго рода:

Если выбрана отрицательная сторона поверхности, то знак интеграла меняется:

Аналогично вычисляются два других отдельных интеграла - слагаемых общего:

Пример 2.

,

где σ - верхняя сторона части плоскости , отсечённая плоскостями y = 0 и y = 4 и находящаяся в первом октанте.

Решение. Чертёж - на рисунке сверху. По определению получаем сумму трёх двойных интегралов:

Второй интеграл равен нулю, так как плоскость σ параллельна оси Oy . Поэтому найдём первый и третий интегралы:

Остаётся лишь сложить все отдельные интегралы и получить общий поверхностный интеграл второго рода:

.

Если требуется вычислить поверхностный интеграл второго рода по замкнутой поверхности, можно перейти к тройному интегралу , используя формулу Остроградского. Тогда, если функции P (x,y,z ) , Q (x,y,z ) и R (x,y,z ) и их частные производные , , - непрерывные функции в области W , которую ограничивает замкнутая поверхность σ , то при интегрировании по внешней стороне поверхности в силе равенство

Пример 3. Вычислить поверхностный интеграл второго рода

,

где σ - внешняя сторона поверхности конуса, образованного поверхностью и плоскостью z = 2 .

Решение. Данная поверхность является поверхностью конуса с радиусом R = 2 и высотой h = 2 . Это замкнутая поверхность, поэтому можно использовать формулу Остроградского. Так как P = 3x , Q = 4y , R = −z , то частные производные , , .

Переходим к тройному интегралу, который и решаем:

Больше примеров на вычисление поверхностных интегралов

Пример 4. Вычислить поверхностный интеграл первого рода

где σ - боковая поверхность конуса при .

Решение. Так как частные производные , , 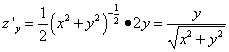то

Сводим данный поверхностный интеграл к двойному:

Проекцией поверхности на плоскость xOy является круг с центром в начале координат и радиусом R = 2 , поэтому при вычислении двойного интеграла перейдём к полярной системе координат. Для этого сделаем замену переменных:

Получаем следующий интеграл, который окончательно и решаем:

Пример 5. Вычислить поверхностный интеграл второго рода

,

где σ - верхняя часть треугольника, образованного пересечением плоскости с координатными плоскостями.

Решение. Данный поверхностный интеграл разделим на сумму двух интегралов

, где

.

Чтобы вычислить интеграл I 1 σ на плоскость yOz . Проекцией является треугольник OCB , который на плоскости yOz ограничивают прямые или , y = 0 и z = 0 . Из уравнения плоскости выводится . Поэтому можем вычислить интеграл I 1 :

Чтобы вычислить интеграл I 2 , построим проекцию поверхности σ на плоскость zOx . Проекцией является треугольник AOC , который ограничивают прямые или , x = 0 и z = 0 . Вычисляем:

Складываем два полученных интеграла и окончательно получаем данный поверхностный интеграл:

.

Пример 6. Вычислить поверхностный интеграл второго рода

,

где σ - внешняя поверхность пирамиды, образованной плоскостью и координатными плоскостями.

Теоретический минимум

Эта тема продолжает обсуждение криволинейных и поверхностных интегралов, начатое в теме " ". Рекомендуется предварительно ознакомиться с той темой. Ввиду большей сложности темы криволинейные и поверхностные интегралы
второго рода рассматриваются отдельно. Здесь обсуждаются поверхностные интегралы второго рода - пожалуй, наиболее сложная интегральная операция в
анализе функций многих переменных. План будет совершенно аналогичен рассмотрению криволинейного интеграла второго рода. Начнём с физических приложений,
а потом уже перейдём к формальному математическому аспекту.

1. Физические приложения поверхностного интеграла второго рода

Самый естественный способ ввести поверхностный интеграл второго рода - рассмотреть поток жидкости через некоторую поверхность. Начнём с простого случая:
жидкость течёт вдоль оси абсцисс с постоянной скоростью . Выделим перпендикулярную течению площадку и найдём массу жидкости, проходящую через
неё за время . За это время через площадку проходит «параллелепипед» высотой и с основанием площадью . Масса этого «параллелепипеда»
равна , где - плотность жидкости.

Теперь пусть жидкость течёт параллельно плоскости под углом к оси абсцисс, но по-прежнему со скоростью . Площадку из предыдущего
случая расположим по-прежнему перпендикулярно оси абсцисс. За время через неё проходит наклонный «параллелепипед» (см. рис. 1). Его масса
равна . Заметим, что введение единичного вектора нормали к площадке позволяет записать .
Вводится формальный вектор элементарной площадки , модуль которого равен , а его направление совпадает с направлением вектора
нормали к площадке. Тогда . Такая запись позволяет не заботиться о направлении вектора скорости жидкости по отношению
к площадке.

Осталось отказаться от малости площадки, через которую течёт жидкость, и от предположение о постоянстве модуля и направления скорости. Тогда
поверхность разбивается на малые части, в пределах которой вектор скорости можно считать постоянным. Масса жидкости, проходящей через поверхность,
приближённо даётся суммой
.
Точная формула получится в пределе разбиения поверхности на бесконечно малые части. Предел является поверхностным интегралом второго рода:
.
При написании этого раздела использован фрагмент учебного материала преподавателя кафедры общей физики, используемый им на семинарских занятиях.

2. Определение поверхностного интеграла второго рода

Теперь о формальном построении интеграла. В связи с тем, что интегрируется по поверхности векторное поле, имеет смысл уточнять, по какой стороне
поверхности вычисляется интеграл (как при вычислении потока жидкости: втекает жидкость внутрь поверхности или вытекает из неё). Поэтому особо уточняется,
что поверхность, по которой проводится интегрирование, должна быть двусторонней или ориентируемой (т.е. лист Мёбиуса как целое не подойдёт). Поверхность
сразу ориентируется, т.е. выбирается определённое направление нормали к поверхности (скажем, если интеграл вычисляется по сфере, то нормаль может быть
направлена из сферы или внутрь сферы). Компоненты поля являются в общей случае функциями точки. Поверхность интегрирования
разбивается на малые части , в каждой части выбирается точка и составляется сумма
,
где - площадь проекции элемента на плоскость , - площадь проекции этого элемента на плоскость , - площадь
проекции этого элемента на плоскость . Проводим суммированием по всем элементам, на которые разбита поверхность:

и переходим к пределу, устремляя к нулю диаметр наибольшей частичной области. Предел является поверхностным интегралом второго рода
.

Покажем, как привести этот интеграл к виду из п.1. Для этого придётся сделать небольшое отступление чисто геометрического характера. Пусть имеется
плоскость , пересекающая оси координат (см. рис. 2). Часть этой плоскости, расположенная в первом октанте, имеет площадь . Требуется найти площади
всех трёх ортогональных проекций данной части плоскости на координатные плоскости. Как известно, площадь проекции фигуры равна произведению площади
самой фигуры и косинуса угла между плоскостью фигуры и плоскостью, на которую она проектируется (см. рис. 3). Т.е. нужно найти углы, которые составляет
плоскость с координатными плоскостями. Угол между двумя плоскостями равен углу между их нормалями. Единичная нормаль к плоскости имеет компоненты,
являющиеся её направляющими косинусами. Поэтому угол между плоскостью и плоскостью равен (см. рис. 2), а значит .
Это же соотношение будет справедливо для бесконечно малых площадок: . И аналогично .
С учётом этих соотношений интеграл примет вид
.
Кстати, эта форма записи более наглядна, поэтому работать будем именно с ней.

Изменение направления нормали на противоположное приводит к тому, что интеграл меняет знак.

3. Вычисление поверхностного интеграла второго рода

После приведения интеграла к форме, содержащей направляющие косинусы нормали к поверхности, задача по сути сводится к записи единичной нормали
с дальнейшим вычислением поверхностного интеграла первого рода. В этих действиях есть некоторая специфика, поэтому подробно разберёмся с вычислением
интегралов такого типа.

Начнём со случая, когда поверхность интегрирования задана явным уравнением, например, . Тогда вектор нормали записывается так:
,
а элемент площади поверхности
.
В результате поверхностный интеграл принимает следующий вид:
, (1)
где - область плоскости , в которую проектируется поверхность интегрирования.

Может быть так, что поверхность интегрирования правильно проектируется на плоскость (и задаётся уравнением ) или на плоскость
(и задаётся уравнением ). Тогда формула, по которой вычисляется интеграл, немного корректируется:
(2)
или
. (3)
Конечно, запоминать такие формулы не рекомендуется: легко что-нибудь перепутать - лучше восстанавливать их применительно к конкретному
расчёту заново, исходя из формулы для вектора нормали и площади малого элемента поверхности.

Есть один выделенный случай, когда поверхность правильно проектируется на все три координатные плоскости, т.е. из уравнения поверхности любая переменная
может быть выражена однозначно. Тогда расчёт существенно упрощается. Обратите внимание на структуру формул (1) - (3). В каждой из них можно выделить три
слагаемых, причём одно из них выглядит проще других. При проектировании поверхности на плоскость это слагаемое, содержащее компоненту
поля ; при проектировании на плоскость это слагаемое, содержащее компоненту ; при проектировании на плоскость это слагаемое,
содержащее компоненту . Если поверхность правильно проектируется на любую координатную плоскость, то мы разобьём интеграл
на три части и спроектируем каждую часть наиболее удобным способом:
.

Наконец, случай параметрического задания поверхности
.
Как и при вычислении поверхностного интеграла первого рода, нужно считать три якобиана:
.
Через них выражаются направляющие косинусы нормали:
,
элемент поверхности
.
Таким образом, для интеграла получаем
,
где - область изменения параметров, соответствующая поверхности интегрирования.

4. Формула Стокса. Формула Остроградского-Гаусса

С поверхностным интегралом второго рода связаны две формулы, находящие разнообразные применения, в том числе в физических приложениях.
Формула Стокса:
,
где ,
поверхность натянута на контур , обход контура согласован с выбором нормали к поверхности по правилу правого винта.
Уточнения требуются, если поверхность интегрирования имеет "дырки".
Формула Грина является частным случаем этой формулы. Кроме того, из формулы Стокса следует условие независимости криволинейного интеграла второго
рода от формы пути.

Формула Остроградского-Гаусса.
Для векторного поля выполняется формула

где поверхность ограничивает объём .

Формула Остроградского-Гаусса имеет разные применения. Остановимся на двух из них. Во-первых, легко доказать, что объём тела может быть вычислен
по формуле

Во-вторых, иногда бывает необходимо вычислить поверхностный интеграл второго рода по незамкнутой поверхности, связанный с громоздким расчётом.
Тогда поверхность замыкают, преобразуют интеграл к тройному и вычитают интеграл по добавленной поверхности (см. пример ниже).

Замечание . Формулы Стокса и Остроградского-Гаусса удобнее записываются в векторном анализе с использованием ротора и дивергенции векторного поля.

Примеры вычисления поверхностных интегралов второго рода

Пример 1. Интеграл по плоскости .. Тогда получим) части эллиптического параболоида (нормаль внешняя).

Перепишем интеграл в виде
.
Поверхность иинтегрирования - эллиптический параболоид - правильно проектируется только на плоскость , поэтому записываем уравнение поверхности в виде
.
Находим единичный вектор нормали:
.