Izračun trojnih integralov: teorija in primeri. Krivočrtni integrali

1) Integral nad površino prve vrste

2) Posebna vektorska polja

3) Stokesov izrek

4) Potencialno polje

Literatura

vektorski potencialni integral polja

Integral nad površino prve vrste

Fizikalni problemi, ki vodijo do površinskega integrala, so lahko dveh vrst:

1) ni povezano s smerjo normale na površino

Na primer, težave pri iskanju mase ali naboja, porazdeljenega po površini:

2) - odvisno od smeri normale - problem iskanja toka tekočine v smeri normale.

Podano: -zvezna funkcija vklopljena

Površina:

1) Površino razdelite na n delov

2) Vzemite točko

3) Izračunajte -gostoto

Zato

kjer je D projekcija na ravnino XOY

Primer. Določite maso, porazdeljeno po površini, z gostoto

Posebna vektorska polja.

1. Razhajanje.
2. Solenoidna polja. Lastnosti.

1. Opredelitev divergence

Ostrogradsky-Gaussov izrek

Poiščite vektorski tok, usmerjen v negativno stran osi Ox, skozi del paraboloida, ki ga odseka ravnina

Opredelitev. Vektorsko polje za vse njegove točke imenujemo solenoidno v domeni. Solenoidno polje je brez virov.

Lastnosti solenoidnih polj.

1. Če je solenoidno polje podano v preprosto povezanem območju, potem je vektorski tok skozi katero koli zaprto površino tega območja enak nič.

Naj bo solenoidno polje v preprosto povezanem območju. Potem vektorski tok skozi katero koli ploskev, ki jo zajema določena kontura G, ni odvisen od vrste te ploskve, ampak je odvisen samo od konture.

Uporabimo Ostrogradsky-Gaussov izrek.

1. Lastnosti vektorske cevi.

Opredelitev. Vektorska črta je črta v vsaki točki, v kateri smer tangente nanjo sovpada s smerjo polja.

vektorska linija.

Vzemimo zaprto konturo na polju in skozi njene točke narišimo vektorske črte

Vse druge vektorske črte, ki potekajo skozi konturne točke, potekajo znotraj ali zunaj cevi.

V primeru toka tekočine je vektorska cev del prostora, ki ga napolni prostornina tekočine, ko se premika.

Intenzivnost vektorske cevi se imenuje poljski tok skozi presek te cevi.

1. Če je polje solenoidno v preprosto povezanem območju

   Tedaj je intenziteta vektorske cevi konstantna vzdolž celotne cevi.

Dokaz:

Bočna površina, vektorske črte so pravokotne. Zato (normala na je normala polja, tj.)

in imajo nasprotne smeri.

Pretok skozi katero koli transverzalo je enak, če je solenoidna.

1. V solenoidnem polju

   vektorske črte se ne morejo začeti ali končati znotraj polja. So bodisi zaprti, imajo konce na meji polja ali imajo neskončne veje.

Dokaz:

V skladu z lastnostjo 3 je jakost cevi enaka, čeprav je prerez v točki M enak nič, pri m M. To je nemogoče, ker neprekinjeno na kateri koli točki.

Stokesov izrek.

Vortex. Rotor.

Naklada.

1. Stokesov izrek

Koncept rotorja ali vrtinca je tesno povezan s konceptom kroženja. Lokalna značilnost polja, povezanega z vrtinčenjem, je rotor.

Ravno polje.

S območje znotraj

hitrostno polje tekoče tekočine

Na polje po dolžini postavimo kolo z rezili. Delci tekočine, ki delujejo na ta rezila, bodo ustvarili navor, katerega celotno delovanje bo povzročilo vrtenje kolesa okoli svoje osi. Rotacijsko delovanje polja hitrosti tekočine v kateri koli točki M bo označeno na tangenti na krožnico, tj. skalarni produkt. Seštevek rotacijskih učinkov tekočine vzdolž celotne konture kolesa bo vodil do koncepta vektorskega kroženja =

Določal bo kotno hitrost vrtenja kolesa, znak kroženja pa bo pokazal, v katero smer se vrti kolo glede na izbrano smer.

Kroženje katerega koli polja določa njegovo rotacijsko sposobnost okoli dane smeri in označuje vrtinčnost polja v tej smeri.

Manjši kot je, večji je kroženje, večja je vrtinčnost.

Največji vrtinec če

Gostota kroženja v točki.

Če je polje prostorsko, potem lahko govorimo o vrtinčenju v smeri.

Vrtinčenje v smeri.

Definicija: v točki se imenuje vektor, katerega projekcija na vsako smer je enaka meji razmerja kroženja vektorskega polja vzdolž konture v ravnem območju, pravokotnem na to smer, na območje S tega območja , ko je območje skrčeno na točki, tj.

Kontura, ki leži v ravnini, pravokotni na vektor

Stokesov izrek. -površinska preprosto povezana regija. - delno gladka kontura v notranjosti, - delno gladka površina, prevlečena z.

Predavanje 7. Površinski integrali.

Problem površinske mase.

Problem površinske mase nas pripelje do površinski integral 1. vrste, tako kot nas je problem mase krivulje pripeljal do krivuljnega integrala prve vrste.

Naj bo površinska gostota f(x, y, z) določena v vsaki točki delno gladke površine s.

1. Vstavimo particijo s v elementarna področja Ds i - elemente particije tako, da nimajo skupnih notranjih točk ( pogoj A).

2. Na elementih pregrade Ds i označimo točke M i . Izračunamo f (M i) = f (x i, y i, z i) in upoštevamo gostoto, ki je konstantna in enaka f (M i) na celotnem predelnem elementu Ds i. Približno izračunajmo maso predelne celice kot f ( M i) Ds i. Približno izračunajmo maso površine s tako, da seštejemo mase celic (sestavimo integralno vsoto). V integralni vsoti je to površina enote celice. Tu se, kot prej, tradicionalno uporablja ista oznaka za samo osnovno celico in njeno območje.

3. Razbitje prečistimo in gremo do limita v integralni vsoti pod pogojem (stanjeB) . Dobimo površinski integral prve vrste, ki je enaka masi površine (razen če je f(M i)>0 na površini).

= .

Izrek o eksistenci. Naj funkcija je zvezna na kosno gladko omejeni površini. Potem površinski integral prve vrste obstaja kot limita integralnih vsot.

= .

Komentiraj. Integral (kot limita integralnih vsot) ni odvisen od:

1) o izbiri površinske razdelitve (dokler je izpolnjen pogoj A),

2) z izbiro označenih točk na pregradnih elementih,

3) o načinu izpopolnjevanja particije (dokler je izpolnjen pogoj B).

Lastnosti površinskega integrala prve vrste.

(po formulaciji in dokazu so podobni lastnostim prej obravnavanih integralov prve vrste).

1) Linearnost.

2) Aditivnost

3) - površina.

4) Če , potem (če, potem),

5) Ocenjevalni izrek.če , To ,

6) Izrek o srednji vrednosti. Naj funkcija je zvezna na kosno gladko omejeni površini. Potem je točka C na površini tako, da

Dokaz. Prve štiri lastnosti dokazujemo podobno kot podobne lastnosti pri dvojnih, trojnih integralih in krivočrtnem integralu prve vrste (z zapisovanjem razmerij v integralnih vsotah in prehodom na limito). Druga lastnost uporablja možnost razdelitve površine na dva dela, tako da noben element razdelitve ne vsebuje mejnih točk teh delov kot svoje notranje točke.

Ocenjevalni izrek izhaja iz lastnosti 3, 4.

Izrek o srednji vrednosti, kot prej, uporablja Weierstrassov in Bolzano-Cauchyjev izrek za funkcije, ki so zvezne na zaprtih omejenih množicah.

Izračun površinskega integrala prve vrste.

Prej smo v drugem predavanju izračunali površino z dvojnim integralom, torej smo integral reducirali na dvojni integral. Sedaj moramo zmanjšati integral na dvojni integral. S ponovnim ponavljanjem istih izračunov z edino razliko, da je pod integralom funkcija, dobimo podobno formulo za površino, določeno z razmerjem

=.

Če je površina podana z enačbo, dobimo formulo na povsem enak način

= . Pri tem moramo upoštevati, da točka (x, y, z) leži na površini.

Primer. Poiščite maso površine homogene poloble , z>0 s konstantno površinsko gostoto W.

Označimo D - krog – projekcijo polkrogle na ravnino OXY.

=.

Površinski integral druge vrste.

Površina se imenuje usmerjeno, če je v vsaki njeni točki normalni vektor na , je zvezna vektorska funkcija na .

Površina se imenuje enostranski, če pri hoji po površini vzdolž konture g normalni vektor spremeni svojo smer v nasprotno.

Površina se imenuje dvostranski,če normalni vektor pri hoji po površini po konturi g ne spremeni svoje smeri.

Primer enostranske ploskve je Möbiusova zanka; primeri dvostranske ploskve so ravnina, krogla, hiperboloidi itd.

Problem pretoka tekočine skozi površino.

Pretok tekočine skozi površino je količina tekočine, ki teče skozi površino na enoto časa.

Tu smo izračunali diferencial pretoka in ga nato integrirali po celotni površini – to je metoda diferencialov pri konstruiranju integrala.

Integral lahko sestavimo z metodo integralnih vsot, kot smo to običajno počeli.

Vstavimo razdelitev regije na elemente tako, da sosednji elementi ne vsebujejo skupnih notranjih točk ( pogoj A),

Na elementih pregrade označimo točko M. Ob predpostavki, da je gibanje delcev tekočine na elementu konstantno in enako (M), približno izračunamo pretok skozi element pregrade in ga seštejemo po elementih, tako da dobimo integralna vsota .

Izboljšajmo particijo pod pogojem ( pogoj B) in pojdite do meje, tako da dobite površinski integral druge vrste

.

Na videz je to površinski integral prve vrste, ima enake lastnosti kot površinski integral prve vrste, ima pa tudi lastnost orientabilnosti. Integral po zunanji strani ploskve se po predznaku razlikuje od integrala po notranji strani ploskve, saj so na različnih straneh ploskve normale na isti točki usmerjene vzdolž iste premice v različne smeri.

Trojni integral je zapisan takole:

Izračunaj trojni integral - pomeni iskanje števila, ki je enako prostornini telesa V ali, kar je isto - območja V .

Skoraj vsak lahko razume pomen izračuna trojnega integrala "na težji način". Natančneje - "pod kožo", še natančneje - v njegovih dihalnih organih - pljučih. Ne glede na to, ali veste ali ne, je v človeških pljučih več kot 700 milijonov pljučnih mešičkov - vezikularnih tvorb, prepletenih z mrežo kapilar. Izmenjava plinov poteka skozi stene alveolov. Zato lahko razmišljamo takole: prostornino plina v pljučih lahko predstavimo kot neko kompaktno območje. Ta volumen je sestavljen iz majhnih volumnov, koncentriranih v alveolih. Ključno vlogo v tej primerjavi igra ogromno število alveolov v pljučih: kot bomo videli v naslednjem odstavku, je skozi tako »ogromno število malenkosti« matematično oblikovan koncept trojnega integrala.

Zakaj se za določanje prostornine telesa uporablja trojni integral? V? Naj območje V razdeljen na n poljubna območja Δ vi, in ta oznaka ne pomeni le vsakega majhnega območja, temveč tudi njegovo prostornino. V vsakem tako majhnem območju je izbrana poljubna točka Mi, A f(Mi)- vrednost funkcije f(M) na tej točki. Sedaj bomo povečali število tako majhnih površin in največji premer Δ vi- nasprotno, zmanjšati. Sestavimo lahko integralno vsoto oblike

Če funkcija f(M) = f(x, l, z) je kontinuirano, bo obstajalo meja integralne vsote zgoraj navedeno vrsto. Ta meja se imenuje trojni integral .

V tem primeru funkcija f(M) = f(x, l, z) imenovan domensko integrabilen V ; V- območje integracije; x, l, z- integracijske spremenljivke, dv(oz dx dy dz ) - element glasnosti.

Izračun trojnega integrala z zmanjševanjem mnogokratnosti

Tako kot pri dvojnih integralih se izračun trojnih integralov zmanjša na izračun integralov nižje mnogokratnosti.

Razmislite o tridimenzionalni regiji V. Spodaj in zgoraj (torej po višini) je to območje omejeno s površinami z = z1 (x, l) in z = z2 (x, l) . Ob straneh (to je v širini) je območje omejeno s površinami l = l1 (x) in l = l2 (x) . In končno, v globino (če gledate območje v smeri osi Ox) - površine x = a in x = b

Za uporabo prehoda na integrale nižje mnogokratnosti je potrebno tridimenzionalno področje V je bil pravilen. Pravilno je, če je premica vzporedna z osjo Oz, prečka mejo regije V na največ dveh točkah. Pravilna tridimenzionalna območja so na primer kvader, elipsoid in tetraeder. Spodnja slika prikazuje pravokotni paralelepiped, ki ga bomo srečali v prvem primeru reševanja naloge.

Za vizualizacijo razlike med pravilnostjo in nepravilnostjo dodamo, da površine regije vzdolž višine pravilne regije ne smejo biti konkavne navznoter. Spodnja slika je primer nepravilnega območja V- enolistni hiperboloid, katerega površina je ravna, vzporedna z osjo Oz(rdeča), seka v več kot dveh točkah.

Upoštevali bomo samo pravilna področja.

Torej območje V- pravilno. Potem za katero koli funkcijo f(x, l, z) , neprekinjeno v regiji V, formula velja

Ta formula vam omogoča, da zmanjšate izračun trojnega integrala na zaporedni izračun notranjega določenega integrala nad spremenljivko z(pri konstantnem x in l) in zunanji dvojni integral nad dvodimenzionalno domeno D .

Če preidemo od dvojnega integrala do ponovljenega, dobimo naslednjo formulo za izračun trojnega integrala:

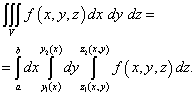
Za izračun trojnega integrala morate torej zaporedno ovrednotiti tri določene integrale.

Ti integrali se izračunajo od najbolj notranjih (čez spremenljivko z) na najbolj oddaljeno (po spremenljivki x). Za lažje razumevanje zaporedja izračunov lahko tri "vgnezdene" integrale zapišemo na naslednji način:

.

Že iz tega zapisa je razvidno, da:

• najprej morate integrirati funkcijo f(x, l, z) po spremenljivki z in vzemite enačbe kot integracijske meje z = z1 (x, l) in z = z2 (x, l) površine, ki omejujejo območje V spodaj in zgoraj;
• l l = l1 (x) in l = l2 (x) površine, ki omejujejo območje V s stranic;
• integrirajte rezultat, dobljen v prejšnjem koraku, nad spremenljivko x in vzemite enačbe kot integracijske meje x = a in x = b površine, ki omejujejo območje V v globino.

Primer 1. Pojdimo od trojnega integrala k iteriranemu integralu

-

zaporedja treh določenih integralov. Ocenite ta ponavljajoči se integral.

rešitev. Izračun iteriranega integrala se vedno začne od zadnjega integrala:

.

Izračunajmo drugi integral – nad spremenljivko l:

.

x:

.

Odgovor: Ta ponovljeni integral in njemu pripadajoči trojni integral sta enaka 10.

Primer 2. Izračunaj trojni integral

,

kje V- paralelepiped, omejen z ravninami x = − 1 , x = + 1 , l = 0 , l = 1 , z = 0 , z = 2 .

rešitev. Meje integracije za vse tri določene integrale so enolično določene z enačbami površin, ki omejujejo paralelepiped. Zato ta trojni integral takoj reduciramo na zaporedje treh določenih integralov:

.

z

.

Integral izračunamo "na sredini" - nad spremenljivko l. Dobimo;

.

Sedaj izračunamo najbolj zunanji integral - nad spremenljivko x:

Odgovor: Ta trojni integral je -2.

Primer 3. Izračunaj trojni integral

,

kje Vx + l + z = 1 in koordinatne ravnine x = 0 , l = 0 , z= 0. Regija V projiciran na ravnino xOy v trikotnik D, kot je prikazano na spodnji sliki.

rešitev. Najprej postavimo meje integracije. Za integral nad spremenljivko z spodnja meja integracije je enolično določena: z= 0. Da dobimo zgornjo mejo, izražamo z od x + l + z = 1 . Dobimo 1 − x − l. Za integral nad spremenljivko l spodnja meja integracije je enolično določena: l= 0. Za pridobitev zgornje meje izrazimo l od x + l + z = 1 , ob upoštevanju tega z= 0 (ker se premica nahaja v ravnini xOy). Dobimo: 1 − x .

Ta trojni integral zmanjšamo na zaporedje treh določenih integralov:

.

Izračunamo najbolj notranji integral – nad spremenljivko z, ob upoštevanju konstant x in y. Dobimo:

.

l. Dobimo:

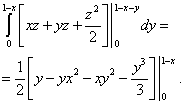
x:

Odgovor: Ta trojni integral je enak 1/8.

Sami izračunajte trojni integral in nato poglejte rešitev

Primer 4. Izračunaj trojni integral

,

kje V- piramida, omejena z ravnino x + l + z = 1 in koordinatne ravnine x = 0 , l = 0 , z = 0 .

Ureditev integracijskih limit pri prehodu na zaporedje treh integralov

Zgodi se, da se učenci, ki nimajo posebnih težav pri neposrednem računanju integralov, ne morejo navaditi na postavljanje limitov integracije pri prehodu s trojnega integrala na zaporedje treh določenih integralov. Ta zadeva zahteva nekaj usposabljanja. V prvem primeru domena integracije V je bil paralelepiped, s katerim je vse jasno: z vseh strani je omejen z ravninami, kar pomeni, da so meje integracije enolično določene z enačbami ravnin. V drugem primeru - piramida: tu je bilo že treba malo bolj razmisliti in izraziti eno od mej iz enačbe. In če območje V ali jih omejujejo neravne površine? Območje je seveda potrebno na določen način pregledati V .

Začnimo z "bolj groznim" primerom, da bi občutili "situacijo blizu boja."

Primer 5. Uredite meje integracije pri prehodu iz trojnega integrala, v katerem regija V- elipsoid

.

rešitev. Naj bo središče elipsoida izhodišče, kot je prikazano na zgornji sliki. Poglejmo elipsoid od spodaj. Od spodaj je omejen s površino, ki je tisti del površine elipsoida, ki se nahaja pod ravnino xOy z in dobljeni izraz z znakom minus bo spodnja meja integracije nad spremenljivko z:

.

Zdaj pa poglejmo elipsoid od zgoraj. Tukaj je omejena s ploskvijo, ki je tisti del elipsoidne ploskve, ki se nahaja nad osjo xOy. Zato moramo izraziti iz enačbe elipsoida z in dobljeni izraz bo zgornja meja integracije nad spremenljivko z:

.

Projekcija elipsoida na ravnino xOy je elipsoid. Njegova enačba:

Za pridobitev spodnje meje integracije nad spremenljivko l, je treba izraziti l iz elipsoidne enačbe in vzemite dobljeni izraz z znakom minus:

.

Za zgornjo mejo integracije nad spremenljivko l isti izraz z znakom plus:

Glede integracije nad spremenljivko x, nato območje V globinsko omejena z ravninami. Zato so meje integracije nad spremenljivko x lahko predstavimo kot koordinate zadnje in sprednje meje območja. V primeru elipsoida bodo to vrednosti dolžin pol osi, vzete z negativnimi in pozitivnimi predznaki a: x1 = − a in x2 = a .

Tako je zaporedje integralov za izračun prostornine elipsoida naslednje:

,

kjer so "yrek prvi", "yrek drugi", "zet prvi" in "zet drugi" zgoraj dobljeni izrazi. Če imate željo in pogum izračunati ta integral in s tem prostornino elipsoida, potem je tukaj odgovor: 4 πabc/3 .

Naslednji primeri niso tako strašljivi kot pravkar obravnavani. Poleg tega ne vključujejo le postavljanja meja integracije, ampak tudi izračun samega trojnega integrala. Preizkusite, kaj ste se naučili, tako da sledite rešitvi grozljivega primera. Še vedno morate razmišljati, ko postavljate meje.

Primer 6. Izračunaj trojni integral

če je integracijska domena omejena z ravninami x + l = 1 , x + 2l = 4 , l = 0 , l = 1 , z = 1 , z = 5 .

rešitev. Primer »letovišča« primerjamo s primerom 5, saj so meje integracije nad »Y« in »Z« enolično določene. Vendar se bomo morali ukvarjati z omejitvami integracije nad "X". Projekcija domene integracije na ravnino xOy je trapez ABCD.

V tem primeru je ugodneje projicirati trapez na os Oj, sicer boste morali za izračun trojnega integrala sliko razdeliti na tri dele. V primeru 4 smo integracijsko regijo začeli pregledovati od spodaj in to je običajen postopek. Toda v tem primeru začnemo pregled od strani ali, če je lažje, postavimo figuro na stran in menimo, da jo gledamo od spodaj. Meje integracije nad "X" lahko najdemo čisto algebraično. Da bi to naredili, izrazimo "x" iz prve in druge enačbe, podane v primeru pogoja. Iz prve enačbe dobimo spodnjo mejo 1 − l, od drugega - zgornji 4 − 2 l.

.

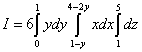Zmanjšajmo ta trojni integral na zaporedje treh določenih integralov: Ox Pozor! V tem primeru skrajni integral ni nad spremenljivko "x", temveč nad spremenljivko "y", "povprečni" integral pa je nad spremenljivko "x"! Tu smo uporabili spremembo vrstnega reda integracije, ki smo jo spoznali pri preučevanju dvojnega integrala. To je posledica dejstva, da smo, kot smo že omenili, integracijsko regijo začeli preučevati ne od spodaj, ampak od strani, to je, da je nismo projicirali na os Oj.

Izračunamo najbolj notranji integral – nad spremenljivko z, ob upoštevanju konstant x in y. Dobimo:

, na os x. Dobimo:

.

Izračunamo povprečni integral – po spremenljivki l:

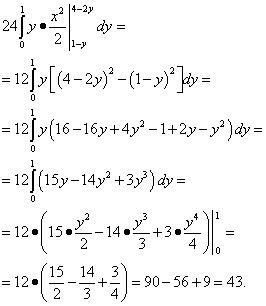
Na koncu izračunamo še zunanji integral – nad spremenljivko

Odgovor: Ta trojni integral je enak 43. Izračunaj trojni integral

,

Primer 7. x = 0 , l = 0 , z = 2 , x + l + z = 4 .

če je območje integracije omejeno na površine V rešitev. Regija (piramida MNRP V) je pravilno. Območje projekcije xOy do letala je trikotnik.

AOB x Spodnje meje integracije za vse spremenljivke so podane v primeru pogoja. Poiščimo zgornjo mejo integracije nad "X". Da bi to naredili, izrazimo "x" iz četrte enačbe, pri čemer menimo, da je "y" enak nič in "ze" enak dve. Dobimo l = 2 − x= 2. Poiščimo zgornjo mejo integracije nad "igro". Če želite to narediti, izrazimo "Y" iz iste četrte enačbe, pri čemer menimo, da je "Z" enak dve in "X" kot spremenljiva vrednost. Dobimo z = 4 − x − l .

. In končno, najdemo zgornjo mejo integracije nad spremenljivko "z". Če želite to narediti, izrazimo "zet" iz iste četrte enačbe, pri čemer menimo, da sta "y" in "zet" spremenljivi količini. Dobimo

.

Izračunamo najbolj notranji integral – nad spremenljivko z, ob upoštevanju konstant x in y. Dobimo:

.

, na os l. Dobimo:

.

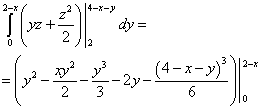Zmanjšajmo ta trojni integral na zaporedje treh določenih integralov: x Izračunamo najbolj zunanji integral – nad spremenljivko

in končno najdemo ta trojni integral:

Odgovor: Ta trojni integral je enak 2.

Sprememba spremenljivk v trojnem integralu in cilindričnih koordinatah Če je projekcija integracijske domene na katero koli od koordinatnih ravnin krog ali del kroga, potem je trojni integral lažje izračunati s prehodom na cilindrične koordinate. Cilindrični koordinatni sistem je posplošitev v vesolje. V cilindričnem koordinatnem sistemu je točka M označen s tremi količinami ( r, φ , z), kje r- razdalja od izhodišča do projekcije n točke M do letala xOy, φ - kot med vektorjem VKLOP in pozitivno smerjo osi Ox, z- točka nanosa M(slika spodaj).

Pravokotne koordinate x, l, z s cilindričnimi koordinatami r, φ , z povežite formule

x = r cos φ ,

l = r greh φ ,

z = z .

Če se želite premakniti na cilindrične koordinate v trojnem integralu, morate izraziti integrand kot funkcijo spremenljivk r, φ , z:

To pomeni, da se prehod iz pravokotnih v cilindrične koordinate izvede na naslednji način:

Trojni integral v cilindričnih koordinatah izračunamo na enak način kot v kartezičnih pravokotnih koordinatah, tako da ga pretvorimo v zaporedje treh določenih integralov:

Primer 8. Izračunaj trojni integral

prehod v cilindrične koordinate, kjer V- območje, omejeno s površinami in.

rešitev. Ker območje V) je pravilno. Območje projekcije xOy se projicira v krog, nato koordinata φ variira od 0 do 2 π , in koordinata r- od r=0 do r=1. Stalna vrednost v prostoru ustreza valju. Ob upoštevanju presečišča tega valja z regijo V, dobimo spremembo ordinate z od z = r do z= 1. Pojdimo na cilindrične koordinate in dobimo.

Delo na terenu

Delo pri premikanju telesa v polju sil po krivulji C je izražena s krivuljnim integralom druge vrste

kjer je sila, ki deluje na telo, je enotski tangentni vektor (slika 1). Zapis pomeni skalarni produkt vektorjev in .

Upoštevajte, da polje sil ni nujno vzrok za gibanje telesa. Telo se lahko premika pod vplivom druge sile. V tem primeru je lahko delo, ki ga opravi sila, včasih negativno.

Če je vektorsko polje podano v koordinatni obliki v obrazcu

potem se terensko delo izračuna po formuli

V posebnem primeru, ko se telo giblje po ravninski krivulji C v ravnini O xy, formula velja

kje

Če je trajektorija C definiran s parametrom t (t pogosto pomeni čas), potem dobi formula za izračun dela obliko

kje t variira v razponu od α do β . Če vektorsko polje potencialno, nato delo, opravljeno za premikanje telesa s točke A do točke B izraženo s formulo

Kje je potencial polja.

Amperov zakon

Krivočrtni integral magnetnega polja z indukcijo vzdolž zaprte zanke C sorazmeren celotnemu toku, ki teče skozi območje, ki ga omejuje tokokrog C(Slika 2). To je izraženo s formulo

kje - magnetna prepustnost vakuuma, enako N/m.

Faradayev zakon

Elektromotorna sila ε induciran v zaprti zanki C, ki je enaka hitrosti spremembe magnetnega pretoka ψ , ki poteka skozi to konturo (slika 3).

Primer

Določite maso žice v obliki odseka iz točke A(1,1) do B(2.4). Masa je porazdeljena vzdolž segmenta z gostoto.

rešitev. Najprej sestavimo parametrično enačbo premice AB.

kje je parameter t spreminja v intervalu. Potem je masa žice

2.4 Fizične aplikacije površinskih integralov

Površinski integrali se uporabljajo v številnih uporabnih izračunih. Zlasti se uporabljajo za izračun

Masa školjke;

Središče mase in vztrajnostni momenti lupine;

Sila privlačnosti in sila pritiska;

Pretok tekočine in snovi skozi površino;

Električni naboj, porazdeljen po površini;

Električna polja (Gaussov izrek v elektrostatiki).

Masa školjke

Naj S Je tanka, gladka lupina. Porazdelitev mase lupine opisuje funkcija gostote. Nato dokončajte masa školjke se izrazi s površinskim integralom prve vrste po formuli

Središče mase in vztrajnostni momenti lupine

Naj masa porazdelitev m v tanki lupini opisuje zvezna funkcija gostote. Koordinate središče mase lupine so določene s formulami

− ti momenti prvega reda o koordinatnih ravninah x = 0, y= 0 in z = 0 oziroma.

Vztrajnostni momenti lupine glede na osi Ox, Oy, Oz so izraženi s formulami

Vztrajnostni momenti lupine glede na ravnine xy, yz, xz so določene s formulami

Površinska gravitacija

Naj bo površina dana S, in na točki ( x 0 , l 0 , z 0), ki ne pripada površini, obstaja telo mase m(Slika 1).

Moč privlačnosti med površino S in točkovno telo m je določen z izrazom

kje, G- gravitacijska konstanta, - funkcija gostote.

Sila pritiska

Predpostavimo, da površina S je podana z vektorjem in je pod vplivom neke tlačne sile (to je lahko jez, krilo letala, stena jeklenke s stisnjenim plinom itd.). Celotno silo, ki jo ustvari pritisk, najdemo s pomočjo površinskega integrala po formuli

Tlak po definiciji deluje v smeri normalnega vektorja na površino S na vsaki točki. Zato lahko pišemo

kjer je enotski normalni vektor na površino S.

Tok tekočine in tok snovi

Če hitrost tekočine obravnavamo kot vektorsko polje, potem tok skozi površino S klical pretok tekočine. Je enaka prostornini tekočine, ki prehaja skozi površino S na časovno enoto in je izražena s formulo

Podobno se imenuje tok vektorskega polja, kjer je ρ gostota tok snovi in je določen z izrazom

Številčno je enaka masi snovi, ki prehaja skozi površino S na časovno enoto.

Površinski naboj

Naj bo količina gostota porazdelitve naboja po površini. Potem polno polnjenje, porazdeljen po prevodni površini S izraženo s formulo

Gaussov izrek

Tok električnega premika skozi zaprto površino S enaka algebraični vsoti vseh nabojev znotraj površine:

kjer je električna poljska jakost, ε − relativna dielektrična konstanta medija, − dielektrična konstanta vakuuma.
Gaussov izrek velja za vse zaprte površine. V primeru površine z zadostno simetrijo ta izrek poenostavlja izračun električnega polja. Gaussov izrek velja za enega glavnih postulatov teorije elektrike. Vključena je v sistem Maxwellovih osnovnih enačb.

Primer

Poiščite maso parabolične lupine, podane z enačbo in ima gostoto.

rešitev.

Uporabimo formulo

Projekcija D(x,y) parabolična površina S do letala xy je krog s polmerom 1 s središčem v izhodišču. Zato lahko pišemo

Če preidemo na polarne koordinate v integrandu, dobimo

Naredimo zamenjavo. Potem. Tukaj u = 1 pri r = 0 in pri r = 1. Torej je integral enak

Zlitine so dvojno, trojčki in bolj zapleteni sistemi... volumetrična teža. Fizično, ta odnos kaže ... včasih podvržen površno strojna obdelava: ... priloženo v podporah. Torej potrebni pogoji geometrijski ...

Krivočrtni integral 1. vrste

1. Dolžina krivulje

Če je funkcija integranda f(x, y, z) ? 1, potem iz definicije krivuljnega integrala 1. vrste ugotovimo, da je v tem primeru enak dolžini krivulje, po kateri se izvaja integracija:

2. Krivulja mase

Ob predpostavki, da je integrand funkcija? (x, y, z) določa gostoto vsake točke krivulje, maso krivulje najdemo s formulo

Primer 23.

Poiščite maso krivulje z linearno gostoto, podano v polarnih koordinatah z enačbo

Uporabimo formulo (86):

3. Najdemo trenutke krivulje l, razmišljamo na enak način kot v primeru ravnega območja:

Statični momenti ravninske krivulje l glede na osi Ox in Oy;

• - (88)
• - vztrajnostni moment prostorske krivulje glede na izhodišče;

• - vztrajnostni momenti krivulje glede na koordinatne osi.
• 4. Koordinate središča mase krivulje izračunamo s pomočjo formul

Krivočrtni integral 2. vrste

to je krivocrtni integral 2. vrste.

Primer 24.

Izračunajte delo, ki ga opravi sila, ki deluje na točko, ki se giblje premočrtno od točke A(2; 1; 0) do točke B(-3; 2; 1).

Parametrične enačbe premice AB imajo obliko:

V tem primeru je dx = -5dt, dy = dt, dz = dt.

• 4. Površinski integral 1. vrste
• 1. Območje ukrivljene površine, katere enačba je

z = f(x, y), lahko najdete v obliki:

• (? - projekcija S na ravnino Oxy).
• 2. Površinska masa

Primer 25.

Poiščite maso površine S: x2 + y2 + z2 = 4, s površinsko gostoto.

Eksplicitno definirajmo površino S: in poiščimo dS:

Površina S je del krogle s polmerom 2 s središčem v izhodišču, izrezan z ravnino. Poiščimo projekcijo te površine na koordinatno ravnino Oxy. Presečišče krogle in ravnine je krog, to je x2 + y2 = 1. Posledično je projekcija S na ravnino Oxy krog enotskega polmera s središčem v izhodišču.

Izračunajmo maso površine v polarnih koordinatah:

3. Trenutki:

Statični momenti površine glede na koordinatne ravnine Oxy, Oxz, Oyz;

Vztrajnostni momenti površine glede na koordinatne osi;

Vztrajnostni momenti površine glede na koordinatne ravnine;

• - vztrajnostni moment površine glede na izvor.
• 4. Koordinate središča mase površine:

Komentiraj. Ker so formule, ki določajo vrednosti geometrijskih in fizikalnih veličin z uporabo integralov, izpeljane z enakimi tehnikami za integrale vseh obravnavanih vrst, je njihova podrobna izpeljava podana šele na začetku poglavja. Če želite, lahko izvedete podobno razmišljanje za trojne, krivočrtne in površinske integrale ter dobite vse podane formule brez podrobne izpeljave.