Vsota kotov trikotnika. Celotne lekcije – Hipermarket znanja

Dokaz

Naj ABC" - poljuben trikotnik. Pojdimo skozi vrh B črta vzporedna s črto A.C. (tako premico imenujemo evklidska premica). Označimo točko na njem D tako da točke A in D ležijo na nasprotnih straneh ravne črte B.C..Koti DBC in ACB enako kot notranja navzkrižno ležeča, ki jo tvori sekanta B.C. z vzporednimi črtami A.C. in BD. Zato je vsota kotov trikotnika pri ogliščih B in Z enak kotu ABD.Vsota vseh treh kotov trikotnika je enaka vsoti kotov ABD in BAC. Ker so ti koti notranji enostranski za vzporedne A.C. in BD pri sekanti AB, potem je njuna vsota 180°. Izrek je dokazan.

Posledice

Iz izreka sledi, da ima vsak trikotnik dva ostra kota. Dejansko z dokazom s protislovjem predpostavimo, da ima trikotnik samo en oster kot ali pa sploh nima ostrih kotov. Potem ima ta trikotnik najmanj dva kota, od katerih ima vsak vsaj 90°. Vsota teh kotov ni manjša od 180°. Toda to je nemogoče, saj je vsota vseh kotov trikotnika 180°. Q.E.D.

Posplošitev v teorijo simpleksa

Kje je kot med ploskvama i in j simpleksa.

Opombe

• Na krogli vsota kotov trikotnika vedno presega 180°, razlika se imenuje sferični presežek in je sorazmerna s površino trikotnika.
• V ravnini Lobačevskega je vsota kotov trikotnika vedno manjša od 180°. Razlika je tudi sorazmerna s površino trikotnika.

Glej tudi

Fundacija Wikimedia.

2010.

Oglejte si, kaj je "Izrek o vsoti kotov trikotnika" v drugih slovarjih:

Lastnost mnogokotnikov v evklidski geometriji: Vsota kotov n trikotnika je 180°(n 2). Vsebina 1 Dokaz 2 Opomba ... Wikipedia

Pitagorov izrek je eden temeljnih izrekov evklidske geometrije, ki določa razmerje med stranicami pravokotnega trikotnika. Vsebina 1 ... Wikipedia

Pitagorov izrek je eden temeljnih izrekov evklidske geometrije, ki določa razmerje med stranicami pravokotnega trikotnika. Vsebina 1 Izjave 2 Dokazi ... Wikipedia

Ta izraz ima druge pomene, glejte Trikotnik (pomeni). Trikotnik (v evklidskem prostoru) je geometrijski lik, sestavljen iz treh odsekov, ki povezujejo tri točke, ki ne ležijo na isti premici. Tri pike,... ... Wikipedia

Standardni zapis Trikotnik je najpreprostejši mnogokotnik, ki ima 3 oglišča (kote) in 3 stranice; del ravnine, ki ga omejujejo tri točke, ki ne ležijo na isti premici, in trije odseki, ki te točke povezujejo v parih. Oglišča trikotnika ... Wikipedia

starogrški matematik. Deloval v Aleksandriji v 3. stoletju. pr. n. št e. Glavno delo "Načela" (15 knjig), ki vsebuje temelje starodavne matematike, elementarne geometrije, teorije števil, splošne teorije razmerij in metode določanja površin in volumnov,... ... Enciklopedični slovar

- (umrl med 275 in 270 pr. n. št.) starogrški matematik. Podatki o času in kraju njegovega rojstva niso dosegli nas, vendar je znano, da je Evklid živel v Aleksandriji, razcvet njegove dejavnosti pa se je zgodil med vladavino Ptolemeja I. v Egiptu... ... Veliki enciklopedični slovar

Geometrija je podobna evklidski geometriji v tem, da definira gibanje likov, vendar se od evklidske geometrije razlikuje po tem, da je eden od njenih petih postulatov (drugi ali peti) nadomeščen z njegovo negacijo. Negacija enega od evklidskih postulatov ... ... Collierjeva enciklopedija

>>Geometrija: Vsota kotov trikotnika. Popolne lekcije

TEMA LEKCIJE: Vsota kotov trikotnika.

Cilji lekcije:

• Utrjevanje in preverjanje znanja študentov na temo: "Vsota kotov trikotnika";
• Dokaz o lastnostih kotov trikotnika;
• Uporaba te lastnosti pri reševanju preprostih problemov;
• Uporaba zgodovinskega gradiva za razvoj kognitivne dejavnosti učencev;
• Vzgajanje spretnosti natančnosti pri konstruiranju risb.

Cilji lekcije:

• Preizkusite sposobnosti študentov za reševanje problemov.

Načrt lekcije:

1. Trikotnik;
2. Izrek o vsoti kotov trikotnika;
3. Primeri nalog.

Trikotnik.

Datoteka: O.gif Trikotnik- najpreprostejši mnogokotnik, ki ima 3 oglišča (kote) in 3 stranice; del ravnine, ki ga omejujejo tri točke in trije odseki, ki povezujejo te točke v parih.
Tri točke v prostoru, ki ne ležijo na isti premici, ustrezajo eni in samo eni ravnini.
Vsak poligon lahko razdelimo na trikotnike - ta postopek se imenuje triangulacija.
Obstaja del matematike, ki je v celoti posvečen preučevanju zakonov trikotnikov - Trigonometrija.

Izrek o vsoti kotov trikotnika.

File:T.gif Izrek o vsoti kotov trikotnika je klasičen izrek evklidske geometrije, ki pravi, da je vsota kotov trikotnika 180°.

dokaz" :

Naj bo podan Δ ABC. Skozi oglišče B narišimo premico vzporedno z (AC) in na njej označimo točko D tako, da bosta točki A in D ležali na nasprotnih straneh premice BC. Tedaj sta kot (DBC) in kot (ACB) enaka kot notranji križno ležeči z vzporednima premicama BD in AC ter sekanto (BC). Potem je vsota kotov trikotnika pri ogliščih B in C enaka kotu (ABD). Toda kot (ABD) in kot (BAC) pri oglišču A trikotnika ABC sta notranji enostranici z vzporednima premicama BD in AC ter sekanto (AB), njuna vsota pa je 180°. Zato je vsota kotov trikotnika 180°. Izrek je dokazan.

Posledice.

Zunanji kot trikotnika je enak vsoti dveh kotov trikotnika, ki mu ne ležita.

Dokaz:

Naj bo podan Δ ABC. Točka D leži na premici AC tako, da A leži med C in D. Potem je BAD zunanja glede na kot trikotnika pri oglišču A in A + BAD = 180°. Toda A + B + C = 180°, zato je B + C = 180° – A. Zato je BAD = B + C. Posledica je dokazana.

Posledice.

Zunanji kot trikotnika je večji od katerega koli kota trikotnika, ki mu ni soseden.

Naloga.

Zunanji kot trikotnika je kot, ki meji na kateri koli kot trikotnika. Dokaži, da je zunanji kot trikotnika enak vsoti dveh kotov trikotnika, ki mu ne mejita.
(slika 1)

rešitev:

Naj bo v Δ ABC ∠DAС zunanji (slika 1). Potem je ∠DAC = 180°-∠BAC (po lastnosti sosednjih kotov), ​​po izreku o vsoti kotov trikotnika ∠B+∠C = 180°-∠BAC. Iz teh enakosti dobimo ∠DAС=∠В+∠С

Zanimivost:

Vsota kotov trikotnika" :

V geometriji Lobačevskega je vsota kotov trikotnika vedno manjša od 180. V evklidski geometriji je vedno enaka 180. V Riemannovi geometriji je vsota kotov trikotnika vedno večja od 180.

Iz zgodovine matematike:

Evklid (3. stoletje pr. n. št.) v svojem delu "Elementi" daje naslednjo definicijo: "Vzporedne črte so črte, ki so v isti ravnini in se neskončno raztezajo v obe smeri in se ne srečajo na nobeni strani."
Posidonij (1. stoletje pr. n. št.) "Dve ravni črti, ki ležita v isti ravnini, enako oddaljeni druga od druge"
Starogrški znanstvenik Papus (III. stoletje pr. n. št.) je predstavil simbol vzporednih črt - znak =. Pozneje je angleški ekonomist Ricardo (1720-1823) ta simbol uporabil kot znak enačaja.
Šele v 18. stoletju so začeli uporabljati simbol za vzporedne črte - znak ||.
Živa povezava med generacijami se ne prekine niti za trenutek; vsak dan se učimo izkušenj, ki so jih nabrali naši predniki. Stari Grki so na podlagi opazovanj in praktičnih izkušenj sklepali, izražali hipoteze, nato pa so na srečanjih znanstvenikov - simpozijih (dobesedno "praznik") - poskušali te hipoteze utemeljiti in dokazati. Takrat se je pojavila izjava: "Resnica se rodi v sporu."

vprašanja:

1. Kaj je trikotnik?
2. Kaj pravi izrek o vsoti kotov trikotnika?
3. Kolikšen je zunanji kot trikotnika?

Vsota kotov trikotnika- pomembna, a dokaj preprosta tema, ki se poučuje v geometriji 7. razreda. Tema je sestavljena iz izreka, kratkega dokaza in več logičnih posledic. Poznavanje te teme pomaga pri reševanju geometrijskih problemov pri nadaljnjem študiju predmeta.

Izrek - kolikšni so sešteti koti poljubnega trikotnika?

Izrek pravi, da če vzamete kateri koli trikotnik, ne glede na njegovo vrsto, bo vsota vseh kotov vedno 180 stopinj. To je dokazano na naslednji način:

• na primer, vzemite trikotnik ABC, narišite ravno črto skozi točko B, ki se nahaja na vrhu, in jo označite kot "a", ravna črta "a" je strogo vzporedna s stranjo AC;
• med ravno črto "a" in stranicama AB in BC so označeni koti, ki jih označujejo s številkama 1 in 2;
• kot 1 se šteje za enak kotu A, kot 2 pa za enak kotu C, ker se šteje, da ti koti ležijo navzkrižno;
• Tako je vsota med koti 1, 2 in 3 (ki je označena namesto kota B) priznana kot enaka razpetemu kotu z ogliščem B - in je 180 stopinj.

Če je vsota kotov, označenih s številkami, 180 stopinj, potem je vsota kotov A, B in C priznana kot enaka 180 stopinj. To pravilo velja za vsak trikotnik.

Kaj sledi iz geometrijskega izreka

Običajno je izpostaviti več posledic iz zgornjega izreka.

• Če problem obravnava trikotnik s pravim kotom, bo eden od njegovih kotov privzeto enak 90 stopinj, vsota ostrih kotov pa bo prav tako 90 stopinj.
• Če govorimo o pravokotnem enakokrakem trikotniku, bodo njegovi ostri koti, ki skupaj znašajo 90 stopinj, posamezno enaki 45 stopinj.
• Enakostranični trikotnik je sestavljen iz treh enakih kotov, vsak od njih bo enak 60 stopinj, skupaj pa bo 180 stopinj.
• Zunanji kot katerega koli trikotnika bo enak vsoti dveh notranjih kotov, ki mu ne mejita.

Izpeljemo lahko naslednje pravilo: vsak trikotnik ima vsaj dva ostra kota. V nekaterih primerih je trikotnik sestavljen iz treh ostrih kotov, in če sta samo dva, bo tretji kot tup ali pravi.

Oddelki: Matematika

Predstavitev . (1. diapozitiv)

Vrsta lekcije: lekcija učenja nove snovi.

Cilji lekcije:

• Izobraževalni:
  • upoštevajte izrek o vsoti kotov trikotnika,
  • pokazati uporabo izreka pri reševanju nalog.
• Izobraževalni:
  • negovanje pozitivnega odnosa učencev do znanja,
  • Skozi pouk pri učencih razvijati samozavest.
• Razvojni:
  • razvoj analitičnega mišljenja,
  • razvoj »spretnosti za učenje«: uporaba znanja, spretnosti in sposobnosti v izobraževalnem procesu,
  • razvoj logičnega mišljenja, sposobnost jasnega oblikovanja svojih misli.

Oprema: interaktivna tabla, predstavitev, karte.

NAPREDEK POUKA

I. Organizacijski trenutek

– Danes se bomo pri pouku spomnili definicij pravokotnega, enakokrakega in enakostraničnega trikotnika. Ponovimo lastnosti kotov trikotnikov. Z lastnostmi notranjih enostraničnih in notranjih navzkrižno ležečih kotov bomo dokazali izrek o vsoti kotov trikotnika in se ga naučili uporabljati pri reševanju nalog.

II. Ustno(2. diapozitiv)

1) Na slikah poišči pravokotni, enakokraki, enakostranični trikotnik.
2) Določite te trikotnike.
3) Formulirajte lastnosti kotov enakostraničnega in enakokrakega trikotnika.

4) Na sliki KE II NH. (slide 3)

– Določite sekante za te premice
– Poiščite notranje enostranske kote, navzkrižno ležeče notranje kote, poimenujte njihove lastnosti

III. Razlaga nove snovi

Izrek. Vsota kotov trikotnika je 180°

Glede na formulacijo izreka fantje sestavijo risbo, zapišejo pogoj in zaključek. Z odgovori na vprašanja samostojno dokazujejo izrek.

podano: Dokaži:

Dokaz:

1. Skozi oglišče B trikotnika narišemo premico BD II AC.
2. Določite sekante za vzporedne premice.
3. Kaj lahko rečemo o kotih CBD in ACB? (zabeleži)
4. Kaj vemo o kotih CAB in ABD? (zabeleži)
5. Zamenjajte kot CBD s kotom ACB
6. Naredi zaključek.

IV. Dokončaj stavek.(diapozitiv 4)

1. Vsota kotov trikotnika je...
2. V trikotniku je eden od kotov enak, drugi, tretji kot trikotnika pa je enak...
3. Vsota ostrih kotov pravokotnega trikotnika je...
4. Koti enakokrakega pravokotnega trikotnika so enaki...
5. Koti enakostraničnega trikotnika so enaki...
6. Če je kot med stranskimi stranicami enakokrakega trikotnika enak 1000, sta kota pri dnu enaka...

V. Malo zgodovine.(Diapozitivi 5-7)

Trikotnik . Ostri, topi in pravokotni trikotnik.

Noge in hipotenuza. Enakokraki in enakostranični trikotnik.

Vsota kotov trikotnika.

Zunanji kot trikotnika. Znaki enakosti trikotnikov.

Izjemne črte in točke v trikotniku: višine, mediane,

simetrale, mediana e pravokotnice, ortocenter,

težišče, središče včrtanega kroga, središče včrtanega kroga.

Pitagorov izrek. Razmerje stranic v poljubnem trikotniku.

Trikotnik je mnogokotnik s tremi stranicami (ali tremi koti). Stranice trikotnika so pogosto označene z malimi črkami, ki ustrezajo velikim črkam, ki predstavljajo nasprotna oglišča.

Če so vsi trije koti ostri (slika 20), potem je to ostrokotni trikotnik . Če je eden od kotov pravi(C, slika 21), potem pa to pravokotni trikotnik; straneha, bki tvorijo pravi kot, se imenujejo noge; stranicnasproti pravemu kotu se imenuje hipotenuza. Če eden od topih kotov (B, slika 22), potem pa to topokotni trikotnik.


Trikotnik ABC (slika 23) - enakokraki, Če dva njene stranice so enake (a= c); te enake stranice imenujemo stranski, se pokliče tretja oseba osnova trikotnik. Trikotnik ABC (slika 24) – enakostranični, če Vse njene stranice so enake (a = b = c). V splošnem primeru ( a ≠ b ≠ c) imamo scalene trikotnik .

Osnovne lastnosti trikotnikov. V poljubnem trikotniku:

1. Nasproti večje stranice leži večji kot in obratno.

2. Nasproti enakih stranic ležita enaka kota in obratno.

Predvsem vsi koti v enakostranični trikotnika sta enaka.

3. Vsota kotov trikotnika je 180 º .

Iz zadnjih dveh lastnosti sledi, da je vsak kot v enakostranici

trikotnik je 60 º.

4. Nadaljevanje ene od stranic trikotnika (AC, slika 25), dobimo zunanji

kot BCD . Zunanji kot trikotnika je enak vsoti notranjih kotov,

ne meji nanjo : BCD = A + B.

5. katera koli stranica trikotnika je manjša od vsote drugih dveh stranic in večja

njihove razlike (a < b + c, a > b – c;b < a + c, b > a – c;c < a + b,c > a – b).

Znaki enakosti trikotnikov.

Trikotniki so skladni, če so enaki:

a ) dve stranici in kot med njima;

b ) dva vogala in stran, ki meji nanju;

c) tri strani.

Znaki enakosti pravokotnih trikotnikov.

Dva pravokotne trikotnika sta enaka, če je izpolnjen eden od naslednjih pogojev:

1) noge so enake;

2) noga in hipotenuza enega trikotnika sta enaki nogi in hipotenuzi drugega;

3) hipotenuza in ostri kot enega trikotnika sta enaka hipotenuzi in ostremu kotu drugega;

4) krak in sosednji ostri kot enega trikotnika sta enaka kraku in sosednjemu ostremu kotu drugega;

5) noga in nasprotni ostri kot enega trikotnika sta enaka nogi in nasprotni ostri kot drugega.

Čudovite črte in točke v trikotniku.

Višina trikotnik jepravokotno,spuščeno s katerega koli vrha na nasprotno stran ( ali njeno nadaljevanje). Ta stran se imenujeosnova trikotnika . Tri višine trikotnika se vedno sekajona eni točki, poklical ortocenter trikotnik. Ortocenter ostrega trikotnika (točka O , slika 26) se nahaja znotraj trikotnika inortocenter tupokotnega trikotnika (točka O , sl.27) – zunaj; Ortocenter pravokotnega trikotnika sovpada z vrhom pravega kota.

Mediana - To segment , ki povezuje poljubno oglišče trikotnika s sredino nasprotne stranice. Tri mediane trikotnika (AD, BE, CF, slika 28) sekata v eni točki O , ki vedno leži znotraj trikotnika in biti njegov težišče. Ta točka deli vsako mediano v razmerju 2:1, šteto od vrha.

Simetrala - To simetrala kot od vrha do točke križišča z nasprotno stranjo. Tri simetrale trikotnika (AD, BE, CF, slika 29) sekata v eni točki Oh, vedno leži znotraj trikotnika in biti središče včrtanega kroga(glejte razdelek »Vpisanoin opisani poligoni").

Simetrala deli nasprotno stranico na dele, ki so sorazmerni s sosednjimi stranicami ; na primer na sliki 29 AE: CE = AB: BC.

Srednja pravokotna je pravokotnica, potegnjena iz sredine segmentne točke (stranice). Tri pravokotne simetrale trikotnika ABC(KO, MO, NE, slika 30 ) sekata v eni točki O, ki je center opisan krog (točke K, M, N – razpolovišča stranic trikotnika ABC).

V ostrokotnem trikotniku ta točka leži znotraj trikotnika; v tupi - zunaj; v pravokotniku - na sredini hipotenuze. Ortocenter, težišče, središče kroga in včrtana krožnica sovpadajo samo v enakostraničnem trikotniku.

Pitagorov izrek. V pravokotnem trikotniku kvadrat dolžineHipotenuza je enaka vsoti kvadratov dolžin katet.

Dokaz Pitagorovega izreka jasno sledi iz slike 31. Razmislite o pravokotnem trikotniku ABC z nogami a, b in hipotenuzo c.

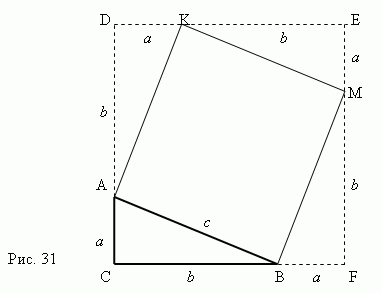
Zgradimo kvadrat AKMB z uporabo hipotenuze AB kot stran. Potemnadaljujte stranice pravokotnega trikotnika ABC tako da dobimo kvadrat CDEF , katerega stranica je enakaa + b .Zdaj je jasno, da je površina kvadrata CDEF je enako ( a+b) 2 . Po drugi strani pa to površina je enaka vsoti področja štiri pravokotne trikotnike in kvadrat AKMB, tj

c 2 + 4 (ab / 2) = c 2 + 2 ab,

od tukaj,

c 2 + 2 ab= (a+b) 2 ,

in končno imamo:

c 2 =a 2 + b 2 .

Razmerje stranic v poljubnem trikotniku.

V splošnem primeru (za poljuben trikotnik) imamo:

c 2 =a 2 + b 2 – 2ab· cos C,

kjer C – kot med stranicamaa in b .