1 Paralelogram ima nasprotna kota. Paralelogram

Dokaz

Najprej narišimo diagonalo AC. Dobimo dva trikotnika: ABC in ADC.

Ker je ABCD paralelogram, velja naslednje:

AD || BC \Desna puščica \kot 1 = \kot 2 kot bi ležal navzkriž.

AB || CD\desna puščica\kot3 =\kot 4 kot bi ležal navzkriž.

Zato je \trikotnik ABC = \trikotnik ADC (po drugem kriteriju: in AC je skupen).

In torej \trikotnik ABC = \trikotnik ADC, potem je AB = CD in AD = BC.

dokazano!

2. Nasprotna kota sta enaka.

Dokaz

Glede na dokaz lastnosti 1 to vemo \kot 1 = \kot 2, \kot 3 = \kot 4. Tako je vsota nasprotnih kotov: \kot 1 + \kot 3 = \kot 2 + \kot 4. Ob upoštevanju, da \trikotnik ABC = \trikotnik ADC dobimo \kotnik A = \kotnik C , \kotnik B = \kotnik D .

dokazano!

3. Diagonale deli presečišče na pol.

Dokaz

Narišimo še eno diagonalo.

Avtor: lastnina 1 vemo, da sta nasprotni stranici enaki: AB = CD. Še enkrat bodite pozorni na navzkrižno ležeče enake kote.

Tako je jasno, da je \trikotnik AOB = \trikotnik COD po drugem kriteriju enakosti trikotnikov (dva kota in stranica med njima). To pomeni, da je BO = OD (nasproti kotov \kota 2 in \kota 1) in AO = OC (nasproti vogalov \kota 3 oziroma \kota 4).

dokazano!

Znaki paralelograma

Če je v vašem problemu prisotna samo ena značilnost, potem je slika paralelogram in lahko uporabite vse lastnosti te figure.

Za boljše pomnjenje upoštevajte, da bo znak paralelograma odgovoril na naslednje vprašanje - "kako ugotoviti?". To je, kako ugotoviti, da je določena figura paralelogram.

1. Paralelogram je štirikotnik, katerega strani sta enaki in vzporedni.

AB = CD; AB || CD\desna puščica ABCD je paralelogram.

Dokaz

Pa poglejmo pobliže. Zakaj AD || pr. n. št.?

\trikotnik ABC = \trikotnik ADC s lastnina 1: AB = CD, AC - skupni in \kotnik 1 = \kotnik 2, ki leži navzkrižno z vzporednikoma AB in CD ter sekanto AC.

Če pa \trikotnik ABC = \trikotnik ADC , potem je \kotnik 3 = \kotnik 4 (leži nasproti AB oziroma CD). In torej AD || BC (\kota 3 in \kota 4 - enaka sta tudi navzkrižno ležeča).

Prvi znak je pravilen.

2. Paralelogram je štirikotnik, katerega nasprotni stranici sta enaki.

AB = CD, AD = BC \desna puščica ABCD je paralelogram.

Dokaz

Razmislimo o tem znaku. Ponovno narišimo diagonalo AC.

Avtor: lastnina 1\trikotnik ABC = \trikotnik ACD .

Iz tega sledi, da: \kot 1 = \kot 2 \Desna puščica AD || B.C. in \kot 3 = \kot 4 \Desna puščica AB || CD, to pomeni, da je ABCD paralelogram.

Drugi znak je pravilen.

3. Paralelogram je štirikotnik, katerega nasprotna kota sta enaka.

\kot A = \kot C , \kot B = \kot D \desna puščica ABCD- paralelogram.

Dokaz

2 \alfa + 2 \beta = 360^(\circ)(ker je ABCD štirikotnik in \kotnik A = \kotnik C , \kotnik B = \kotnik D po pogoju).

Izkazalo se je, da je \alpha + \beta = 180^(\circ) . Toda \alpha in \beta sta notranja enostranska na sekanti AB.

In dejstvo, da \alpha + \beta = 180^(\circ), pomeni tudi, da AD || B.C.

Poleg tega sta \alpha in \beta notranja enostranska na sekanti AD. In to pomeni AB || CD.

Tretji znak je pravilen.

4. Paralelogram je štirikotnik, katerega diagonale deli presečišče na pol.

AO = OC ; BO = OD\desna puščica paralelogram.

Dokaz

BO = OD; AO = OC , \kot 1 = \kot 2 kot navpičnica \Desna puščica \trikotnik AOB = \trikotnik COD, \Desna puščica \kot 3 = \kot 4, in \Rightarrow AB || CD.

Podobno BO = OD; AO = OC, \angle 5 = \angle 6 \Rightarrow \triangle AOD = \triangle BOC \Rightarrow \angle 7 = \angle 8 in \Rightarrow AD || B.C.

Četrti znak je pravilen.

Občinska proračunska izobraževalna ustanova

Savinskaya srednja šola

Raziskovalno delo

Paralelogram in njegove nove lastnosti

Izpolnila: učenka 8B razreda

Srednja šola MBOU Savinskaya

Kuznetsova Svetlana, 14 let

Vodja: učiteljica matematike

Tulčevska N.A.

p. Savino

Ivanovska regija, Rusija

2016

jaz Uvod ________________________________________________ stran 3

II. Iz zgodovine paralelograma ___________________________________stran 4

III Dodatne lastnosti paralelograma ________________________________stran 4

IV. Dokazilo o lastnostih ________________________________ stran 5

V. Reševanje problemov z uporabo dodatnih lastnosti __________stran 8

VI. Uporaba lastnosti paralelograma v življenju ___________________stran 11

VII. Zaključek ________________________________________________stran 12

VIII. Literatura ________________________________________________ stran 13

Uvod

"Med enakopravnimi razumi

pri enakost drugih pogojev

kdor pozna geometrijo, je boljši"

(Blaise Pascal).

Pri pouku geometrije pri temi “Paralelogram” smo si ogledali dve lastnosti paralelograma in tri lastnosti, a ko smo začeli reševati naloge, se je izkazalo, da to ni dovolj.

Imel sem vprašanje: ali ima paralelogram druge lastnosti in kako bodo pomagale pri reševanju problemov?

Odločil sem se preučiti dodatne lastnosti paralelograma in pokazati, kako jih je mogoče uporabiti za reševanje problemov.

Predmet raziskave : paralelogram

Predmet študija : lastnosti paralelograma
Namen dela:

formulacija in dokazovanje dodatnih lastnosti paralelograma, ki se v šoli ne preučujejo;

uporaba teh lastnosti za reševanje problemov.

Naloge:

Preučite zgodovino pojava paralelograma in zgodovino razvoja njegovih lastnosti;

Poiščite dodatno literaturo o obravnavanem vprašanju;

Preučite dodatne lastnosti paralelograma in jih dokažite;

Pokažite uporabo teh lastnosti pri reševanju problemov;

Razmislite o uporabi lastnosti paralelograma v življenju.
Raziskovalne metode:

Delo z izobraževalno in poljudnoznanstveno literaturo, internetnimi viri;

Študij teoretičnega gradiva;

Identifikacija vrste problemov, ki jih je mogoče rešiti z uporabo dodatnih lastnosti paralelograma;

Opazovanje, primerjava, analiza, analogija.

Trajanje študija : 3 meseci: januar-marec 2016

V učbeniku geometrije beremo naslednjo definicijo paralelograma: Paralelogram je štirikotnik, katerega nasprotni strani sta v parih vzporedni.

Beseda "paralelogram" je prevedena kot "vzporedne črte" (iz grških besed Parallelos - vzporednik in gramme - črta), ta izraz je uvedel Evklid. Evklid je v svoji knjigi Elementi dokazal naslednje lastnosti paralelograma: nasprotne stranice in koti paralelograma so enaki, diagonala pa ga razpolovi. Evklid ne omenja presečišča paralelograma. Šele proti koncu srednjega veka je bila razvita celovita teorija paralelogramov in šele v 17. stoletju so se v učbenikih pojavili izreki o paralelogramih, ki so bili dokazani z Evklidovim izrekom o lastnostih paralelograma.

III Dodatne lastnosti paralelograma

V učbeniku geometrije sta podani le 2 lastnosti paralelograma:

Nasprotni koti in stranice so enaki

Diagonali paralelograma se sekata in razpolovita s presečiščem.

V različnih virih o geometriji lahko najdete naslednje dodatne lastnosti:

Vsota sosednjih kotov paralelograma je 180 0

Simetrala kota paralelograma odseka od njega enakokraki trikotnik;

Simetrali nasprotnih kotov paralelograma ležita na vzporednih premicah;

Simetrali sosednjih kotov paralelograma se sekata pod pravim kotom;

Ko se simetrale vseh kotov paralelograma sekajo, tvorijo pravokotnik;

Razdalje od nasprotnih kotov paralelograma do iste diagonale so enake.

Če povežete nasprotni oglišči v paralelogramu z razpolovišči nasprotnih stranic, dobite še en paralelogram.

Vsota kvadratov diagonal paralelograma je enaka dvakratni vsoti kvadratov njegovih sosednjih stranic.

Če v paralelogram narišemo nadmorske višine iz dveh nasprotnih kotov, dobimo pravokotnik.

IV Dokaz lastnosti paralelograma

Vsota sosednjih kotov paralelograma je 180 0

dano:

ABCD – paralelogram

Dokaži:

A+
B=

Dokaz:

A in
B – notranji enostranski koti z vzporednimi premicami BC AD in sekant AB, kar pomeni
A+
B=

podano: ABCD - paralelogram,

Simetrala AK
A.

Dokaži: AVK – enakokraki

Dokaz:

1)
1=
3 (navzkrižno leži na BC AD in sekanta AK ),

2)
2=
3 ker je AK simetrala,

pomeni 1=
2.

3) ABC - enakokraki, ker sta 2 kota trikotnika enaka

. Simetrala kota paralelograma odseka enakokraki trikotnik

podano: ABCD je paralelogram,

AK – simetrala A,

CP - simetrala C.

Dokaži: AK ║ SR

Dokaz:

1) 1=2, ker je AK simetrala

2) 4=5 ker CP – simetrala

3) 3=1 (navzkrižno ležeči koti pri

BC ║ AD in AK-sekant),

4) A =C (po lastnosti paralelograma), kar pomeni 2=3=4=5.

4) Iz odstavkov 3 in 4 sledi, da je 1 = 4, ti koti pa ustrezajo ravnim črtam AK in CP ter sekanti BC,

to pomeni AK ║ CP (na podlagi vzporednosti črt)

. Simetrale nasprotnih kotov paralelograma ležijo na vzporednih premicah

Simetrale sosednjih kotov paralelograma se sekata pod pravim kotom

podano: ABCD - paralelogram,

AK-simetrala A,

Simetrala DP D

Dokaži: DP AK.

Dokaz:

1) 1=2, ker AK - simetrala

Naj bo 1=2=x, potem je A=2x,

2) 3=4, ker D Р – simetrala

Naj bo 3=4=y, potem je D=2y

3) A + D =180 0, ker vsota sosednjih kotov paralelograma je 180

2) Razmislite A OD

1+3=90 0 , torej
<5=90 0 (сумма углов треугольников равна 180 0)

5. Simetrale vseh kotov paralelograma ob sekanju tvorijo pravokotnik

podano: ABCD - paralelogram, AK-simetrala A,

DP-simetrala D,

CM simetrala C,

BF - simetrala B .

Dokaži: KRNS - pravokotnik

Dokaz:

Na podlagi prejšnje lastnosti 8=7=6=5=90 0 ,

pomeni, da je KRNS pravokotnik.

Razdalje od nasprotnih kotov paralelograma do iste diagonale so enake.

podano: ABCD-paralelogram, AC-diagonala.

VK AC, D.P. A.C.

Dokaži: BC=DP

Dokaz: 1) DCP = KAB, kot notranji križi, ki ležijo z AB ║ CD in sekanto AC.

2) AKB= CDP (vzdolž stranice in dveh sosednjih kotov AB=CD CD P=AB K).

In v enakih trikotnikih so ustrezne stranice enake, kar pomeni DP=BK.

Če povežete nasprotni oglišči v paralelogramu z razpolovišči nasprotnih stranic, dobite še en paralelogram.

podano: ABCD paralelogram.

Dokaži: VKDR je paralelogram.

Dokaz:

1) BP=KD (AD=BC, točki K in P

te stranice razdelite na pol)

2) BP ║ KD (leži na AD pr. n. št.)

Če sta nasprotni stranici štirikotnika enaki in vzporedni, potem je štirikotnik paralelogram.

Če v paralelogram narišemo nadmorske višine iz dveh nasprotnih kotov, dobimo pravokotnik.

Vsota kvadratov diagonal paralelograma je enaka dvakratni vsoti kvadratov njegovih sosednjih stranic.

podano: ABCD je paralelogram. BD in AC sta diagonali.

Dokaži: AC 2 +ВD 2 =2(AB 2 + AD 2 )

Dokaz: 1)VPRAŠAJ: A.C. ²=
+

2)B RD : BD 2 = B R 2 + RD 2 (po Pitagorovem izreku)

3) A.C. ²+ BD ²=SK²+A K²+B Р²+РD ²

4) SC = BP = N(višina )

5) AC 2 +BD 2 = H 2 + A TO 2 + H 2 +PD 2

6) Naj D K=A P=x, Potem C TOD : H 2 = CD 2 - X 2 po Pitagorovem izreku )

7) AC²+BD ² = CD 2 - x²+ AK 1 ²+ CD 2 -X 2 +PD 2 ,

AC²+BD ²=2СD 2 -2x 2 + A TO 2 +PD 2

8) A TO=AD+ X, RD=AD- X,

AC²+BD ² =2CD 2 -2x 2 +(AD +x) 2 +(AD -X) 2 ,

AC²+ IND²=2 ZD²-2 X² + AD 2 +2 AD X+ X 2 +AD 2 -2 AD X+ X 2 ,
AC²+ IND²=2CD 2 +2 AD 2 =2(CD 2 +AD 2 ).

V . Reševanje problemov z uporabo teh lastnosti

Točka presečišča simetral dveh kotov paralelograma, ki ležita na eni strani, pripada nasprotni strani. Najkrajša stranica paralelograma je 5 . Poiščite njegovo večjo stran.

podano: ABCD je paralelogram,

AK – simetrala
A,

D K – simetrala
D, AB=5

Najdi: Sonce

odločitev

rešitev

Ker AK - simetrala
In potem je ABC enakokrak.

Ker D K – simetrala
D, torej DCK - enakokraki

DC =C K= 5

Potem je BC=VC+SC=5+5 = 10

Odgovor: 10

2. Poiščite obseg paralelograma, če simetrala enega od njegovih kotov deli stranico paralelograma na segmenta 7 cm in 14 cm.

1 primer

podano:
A,

VK=14 cm, KS=7 cm

Najdi: P paralelogram

rešitev

VS=VK+KS=14+7=21 (cm)

Ker AK – simetrala
In potem je ABC enakokrak.

AB=BK= 14 cm

Potem je P=2 (14+21) =70 (cm)

dogajanje

podano: ABCD je paralelogram,

D K – simetrala
D

VK=14 cm, KS=7 cm

Najdi: P paralelogram

rešitev

VS=VK+KS=14+7=21 (cm)

Ker D K – simetrala
D, torej DCK - enakokraki

DC =C K= 7

Potem je P = 2 (21+7) = 56 (cm)

odgovor: 70cm ali 56cm

3. Stranici paralelograma sta 10 cm in 3 cm Simetrali dveh kotov, ki mejita na večjo stranico, delita nasprotno stranico na tri odseke. Poiščite te segmente.

1 primer: simetrali se sekata zunaj paralelograma

podano: ABCD – paralelogram, AK – simetrala
A,

D K – simetrala
D , AB=3 cm, BC=10 cm

Najdi: VM, MN, NC

rešitev

Ker AM - simetrala
In potem je AVM enakokrak.

Ker DN – simetrala
D, torej DCN - enakokraki

DC=CN=3

Potem je MN = 10 – (BM +NC) = 10 – (3+3)=4 cm

2. primer: simetrale sekajo znotraj paralelograma

Ker AN - simetrala
In potem je ABN enakokrak.

AB=Bn = 3 D

In drsno rešetko je treba premakniti na zahtevano razdaljo v vratih

Paralelogramski mehanizem- štiripalični mehanizem, katerega povezave tvorijo paralelogram. Uporablja se za izvajanje translacijskega gibanja z zgibnimi mehanizmi.

Paralelogram s fiksno povezavo- en člen je negiben, nasprotni pa se ziba in ostane vzporeden z negibnim. Dva paralelograma, povezana eden za drugim, dajeta končnemu členu dve stopnji svobode, tako da je vzporeden s stacionarnim členom.

Primeri: avtobusni brisalci, viličarji, stojala, obešalniki, avtomobilske obese.

Paralelogram s fiksnim sklepom- uporablja se lastnost paralelograma, da ohranja konstantno razmerje razdalj med tremi točkami. Primer: risalni odjemnik toka - naprava za skaliranje risb.

Romb- vsi členi so enake dolžine, približevanje (krčenje) para nasprotnih tečajev povzroči razmik drugih dveh tečajev. Vse povezave delujejo kompresirano.

Primeri - avtomobilska dvigalka v obliki romba, tramvajski odjemnik toka.

Škarje oz Mehanizem v obliki črke X, znan tudi kot Nürnberške škarje- izvedba romb - dva člena, povezana na sredini s tečajem. Prednosti mehanizma so kompaktnost in enostavnost, pomanjkljivost pa je prisotnost dveh drsnih parov. Dva (ali več) takih zaporedno povezanih mehanizmov tvorita diamant(e) na sredini. Uporablja se v dvigalih in otroških igračah.

VII Zaključek

Kdo je študiral matematiko že od otroštva?

razvija pozornost, trenira možgane,

lastno voljo, goji vztrajnost

in vztrajnost pri doseganju ciljev

A. Markuševiča

Pri delu sem dokazal dodatne lastnosti paralelograma.

Prepričan sem bil, da lahko z uporabo teh lastnosti hitreje rešiš težave.

Na primerih reševanja konkretnih problemov sem pokazal, kako se te lastnosti uporabljajo.

Veliko sem se naučil o paralelogramu, ki ga v našem učbeniku geometrije ni

Da je znanje geometrije v življenju zelo pomembno, sem se prepričal na primerih uporabe lastnosti paralelograma.

Namen mojega raziskovalnega dela je bil dosežen.

O pomenu matematičnega znanja priča dejstvo, da je bila ustanovljena nagrada za tistega, ki izda knjigo o človeku, ki je vse življenje preživel brez pomoči matematike. Te nagrade ni prejel še nihče.

VIII Literatura

Paralelogram je štirikotnik, katerega nasprotni strani sta v parih vzporedni. Površina paralelograma je enaka produktu njegove osnove (a) in višine (h). Njegovo ploščino lahko najdete tudi skozi dve stranici in kot ter skozi diagonale.

Lastnosti paralelograma

1. Nasprotni stranici sta enaki

Najprej narišimo diagonalo \(AC\) . Dobimo dva trikotnika: \(ABC\) in \(ADC\).

Ker je \(ABCD\) paralelogram, velja naslednje:

\(AD || BC \Desna puščica \kot 1 = \kot 2\) kot bi ležal navzkriž.

\(AB || CD \desna puščica \angle3 = \angle 4\) kot bi ležal navzkriž.

Zato (glede na drugo merilo: in \(AC\) je skupno).

In to pomeni \(\trikotnik ABC = \trikotnik ADC\), nato \(AB = CD\) in \(AD = BC\) .

2. Nasprotna kota sta enaka

Glede na dokaz lastnosti 1 to vemo \(\kot 1 = \kot 2, \kot 3 = \kot 4\). Tako je vsota nasprotnih kotov: \(\kot 1 + \kot 3 = \kot 2 + \kot 4\). Glede na to \(\trikotnik ABC = \trikotnik ADC\) dobimo \(\kot A = \kot C \) , \(\kot B = \kot D \) .

3. Diagonale deli presečišče na pol

Avtor: lastnina 1 vemo, da sta nasprotni stranici enaki: \(AB = CD\) . Še enkrat bodite pozorni na navzkrižno ležeče enake kote.

Tako je jasno, da \(\trikotnik AOB = \trikotnik COD\) po drugem kriteriju enakosti trikotnikov (dva kota in stranica med njima). To je \(BO = OD\) (nasproti kotov \(\kot 2\) in \(\kot 1\) ) in \(AO = OC\) (nasproti kotov \(\kot 3\) in \( \kot 4\) oziroma).

Znaki paralelograma

Če je v vašem problemu prisotna samo ena značilnost, potem je slika paralelogram in lahko uporabite vse lastnosti te figure.

Za boljše pomnjenje upoštevajte, da bo znak paralelograma odgovoril na naslednje vprašanje - "kako ugotoviti?". To je, kako ugotoviti, da je določena figura paralelogram.

1. Paralelogram je štirikotnik, katerega strani sta enaki in vzporedni

\(AB = CD\) ; \(AB || CD \desna puščica ABCD\)- paralelogram.

Pa poglejmo pobliže. Zakaj \(AD || BC \)?

\(\trikotnik ABC = \trikotnik ADC\) Avtor: lastnina 1: \(AB = CD \) , \(\kot 1 = \kot 2 \), ki leži navzkrižno, ko sta \(AB \) in \(CD \) ter sekanta \(AC \) vzporedna.

Ampak če \(\trikotnik ABC = \trikotnik ADC\), potem \(\kot 3 = \kot 4 \) (ležita nasproti \(AD || BC \) (\(\kota 3 \) in \(\kota 4 \) - tista, ki ležita navzkrižno, sta prav tako enaka).

Prvi znak je pravilen.

2. Paralelogram je štirikotnik, katerega nasprotni stranici sta enaki

\(AB = CD \) , \(AD = BC \desna puščica ABCD \) je paralelogram.

Razmislimo o tem znaku. Ponovno narišimo diagonalo \(AC\).

Avtor: lastnina 1\(\trikotnik ABC = \trikotnik ACD\).

Iz tega sledi, da: \(\kot 1 = \kot 2 \desna puščica AD || BC \) in \(\kot 3 = \kot 4 \Desna puščica AB || CD \), to pomeni, da je \(ABCD\) paralelogram.

Drugi znak je pravilen.

3. Paralelogram je štirikotnik, katerega nasprotna kota sta enaka

\(\kot A = \kot C\) , \(\kot B = \kot D \Desna puščica ABCD\)- paralelogram.

\(2 \alfa + 2 \beta = 360^(\circ) \)(ker \(\kot A = \kot C\) , \(\kot B = \kot D\) po pogoju).

Izkazalo se je,. Toda \(\alpha \) in \(\beta \) sta notranja enostranska v sekanti \(AB \) .

In kaj \(\alfa + \beta = 180^(\circ) \) pravi tudi, da \(AD || BC \) .

Paralelogram je štirikotnik, katerega nasprotni stranici sta vzporedni, tj. ležijo na vzporednih premicah

Lastnosti paralelograma: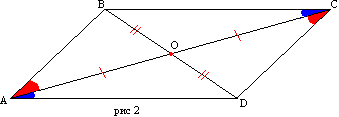
Izrek 22. Nasprotni stranici paralelograma sta enaki.
Dokaz. V paralelogramu ABCD narišemo diagonalo AC. Trikotnika ACD in ACB sta skladna, saj imata skupno stranico AC in dva para enakih kotov. zraven: ∠ CAB=∠ ACD, ∠ ACB=∠ DAC (kot navzkrižna kota z vzporednicama AD in BC). To pomeni, da je AB = CD in BC = AD, kot ustrezni stranici enakih trikotnikov itd. Iz enakosti teh trikotnikov sledi tudi, da so ustrezni koti trikotnikov enaki:
Izrek 23. Nasprotna kota paralelograma sta enaka: ∠ A=∠ C in ∠ B=∠ D.
Enakost prvega para izhaja iz enakosti trikotnikov ABD in CBD, drugega pa ABC in ACD.
Izrek 24. Sosednja kota paralelograma, tj. seštevek kotov ob eni strani znaša 180 stopinj.
To je tako, ker so notranji enostranski koti.
Izrek 25. Diagonali paralelograma se razpolovita v presečni točki.
Dokaz. Razmislite o trikotnikih BOC in AOD. Po prvi lastnosti AD=BC ∠ OAD=∠ OCB in ∠ ODA=∠ OBC križno ležeči za vzporednici AD in BC. Zato sta trikotnika BOC in AOD enaka v stranskih in sosednjih kotih. To pomeni BO=OD in AO=OS, kot ustrezne stranice enakih trikotnikov itd.

Znaki paralelograma
Izrek 26. Če sta nasprotni strani štirikotnika v parih enaki, je štirikotnik paralelogram.
Dokaz. Naj ima štirikotnik ABCD stranice AD in BC, AB in CD enake (slika 2). Narišimo diagonalo AC. Trikotnika ABC in ACD sta na treh stranicah enaka. Tedaj sta kota BAC in DCA enaka in je torej AB vzporedna s CD. Vzporednost stranic BC in AD izhaja iz enakosti kotov CAD in ACB.
Izrek 27. Če sta nasprotna kota štirikotnika v parih enaka, je štirikotnik paralelogram.
Naj bo ∠ A=∠ C in ∠ B=∠ D. Ker ∠ A+∠ B+∠ C+∠ D=360 o, potem ∠ A+∠ B=180 o in stranici AD in BC sta vzporedni (glede na vzporednost ravnih črt). Dokazali bomo tudi vzporednost stranic AB in CD ter ugotovili, da je ABCD po definiciji paralelogram.
Izrek 28. Če sosednji vogali štirikotnika, tj. Seštevek kotov, ki mejijo na eno stran, je 180 stopinj, potem je to paralelogram.
Če seštevek notranjih enostranskih kotov znaša 180 stopinj, sta ravni črti vzporedni. Torej je AB vzporeden s CD in BC je vzporeden z AD. Štirikotnik se po definiciji izkaže za paralelogram.
Izrek 29. Če se diagonali štirikotnika v presečišču razpolovita, je štirikotnik paralelogram.
Dokaz. Če je AO = OC, BO = OD, sta trikotnika AOD in BOC enaka, saj imata enake (navpične) kote pri oglišču O, zaprtem med pari enakih stranic. Iz enakosti trikotnikov sklepamo, da sta AD in BC enaka. Stranici AB in CD sta prav tako enaki in štirikotnik se po 1. kriteriju izkaže za paralelogram.
Izrek 30. Če ima štirikotnik par enakih, vzporednih stranic, potem je to paralelogram.
Naj bosta stranici AB in CD štirikotnika ABCD vzporedni in enaki. Narišimo diagonali AC in BD. Iz vzporednosti teh premic sledi, da sta navzkrižna kota ABO = CDO in BAO = OCD enaka. Trikotnika ABO in CDO sta enaka v stranskih in priležnih kotih. Zato je AO=OS, VO=ОД, tj. Diagonali sta razdeljeni na pol s presečiščem in štirikotnik se izkaže za paralelogram po kriteriju 4.

V geometriji obravnavamo posebne primere paralelogramov.

Paralelogram je štirikotnik, katerega nasprotni strani sta v parih vzporedni. Naslednja slika prikazuje paralelogram ABCD. Ima stranico AB vzporedno s stranico CD in stranico BC vzporedno s stranico AD.

Kot ste morda uganili, je paralelogram konveksen štirikotnik. Razmislimo o osnovnih lastnostih paralelograma.

Lastnosti paralelograma

1. V paralelogramu so nasprotni koti in nasprotne stranice enaki. Dokažimo to lastnost – razmislimo o paralelogramu, predstavljenem na naslednji sliki.

Diagonala BD ga deli na dva enaka trikotnika: ABD in CBD. Vzdolž stranice BD in obeh kotov, ki ležita na njej, sta enaka, saj kota navzkrižno ležita na sekanti BD vzporednih premic BC in AD oziroma AB in CD. Zato je AB = CD in
pr. Kr. = AD. In iz enakosti kotov 1, 2, 3 in 4 sledi, da je kot A = kot 1 + kot 3 = kot 2 + kot 4 = kot C.

2. Diagonali paralelograma sta razdeljeni na pol s presečiščem. Naj bo točka O presečišče diagonal AC in BD paralelograma ABCD.

Potem sta si trikotnik AOB in trikotnik COD enaka, vzdolž stranice in dveh sosednjih kotov. (AB = CD, ker sta to nasprotni strani paralelograma. In kot 1 = kot 2 in kot 3 = kot 4 sta kot navzkrižna kota, ko premici AB in CD sekata sekanti AC oziroma BD.) Iz tega sledi, da je AO = OC in OB = OD, kar je bilo treba dokazati.

Vse glavne lastnosti so prikazane na naslednjih treh slikah.