პარალელოგრამი და მისი თვისებები. პარალელოგრამის ფართობი

პარალელოგრამი არის ოთხკუთხედი, რომლის მოპირდაპირე გვერდები პარალელურია, ე.ი. დაწექი პარალელურ ხაზებზე

პარალელოგრამის თვისებები: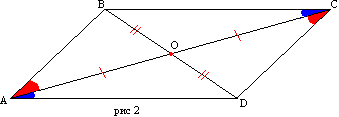
თეორემა 22. პარალელოგრამის მოპირდაპირე მხარეები ტოლია.
მტკიცებულება. ABCD პარალელოგრამაზე ვხატავთ AC დიაგონალს. სამკუთხედები ACD და ACB თანმიმდევრულია, რადგან აქვთ საერთო გვერდი AC და ორი წყვილი თანაბარი კუთხე. მის მიმდებარედ: ∠ CAB=∠ ACD, ∠ ACB=∠ DAC (როგორც ჯვარედინი კუთხეები AD და BC პარალელური ხაზებით). ეს ნიშნავს, რომ AB = CD და BC = AD, როგორც ტოლი სამკუთხედების შესაბამისი გვერდები და ა.შ. ამ სამკუთხედების ტოლობიდან ასევე გამოდის, რომ სამკუთხედების შესაბამისი კუთხეები ტოლია:
თეორემა 23. პარალელოგრამის საპირისპირო კუთხეები ტოლია: ∠ A=∠ C და ∠ B=∠ D.
პირველი წყვილის ტოლობა მოდის ABD და CBD სამკუთხედების ტოლობიდან, ხოლო მეორე - ABC და ACD.
თეორემა 24. პარალელოგრამის მიმდებარე კუთხეები, ე.ი. ერთი მხარის მიმდებარე კუთხეები ემატება 180 გრადუსს.
ეს იმიტომ ხდება, რომ ისინი შიდა ცალმხრივი კუთხეებია.
თეორემა 25. პარალელოგრამის დიაგონალები ერთმანეთს კვეთენ მათი გადაკვეთის წერტილში.
მტკიცებულება. განვიხილოთ სამკუთხედები BOC და AOD. პირველი თვისების მიხედვით AD=BC ∠ OAD=∠ OCB და ∠ ODA=∠ OBC ჯვარედინზე დევს პარალელური ხაზებისთვის AD და BC. ამრიგად, BOC და AOD სამკუთხედები ტოლია გვერდით და მიმდებარე კუთხით. ეს ნიშნავს BO=OD და AO=OS, როგორც ტოლი სამკუთხედების შესაბამისი გვერდები და ა.შ.

პარალელოგრამის ნიშნები
თეორემა 26. თუ ოთხკუთხედის საპირისპირო გვერდები წყვილებში ტოლია, მაშინ ის პარალელოგრამია.
მტკიცებულება. დაე, ოთხკუთხედს ABCD ჰქონდეს გვერდები AD და BC, AB და CD შესაბამისად ტოლი (ნახ. 2). დავხატოთ AC დიაგონალი. სამკუთხედები ABC და ACD ტოლია სამი მხრიდან. მაშინ კუთხეები BAC და DCA ტოლია და, შესაბამისად, AB არის CD-ის პარალელურად. BC და AD გვერდების პარალელიზმი გამომდინარეობს CAD და ACB კუთხეების ტოლობიდან.
თეორემა 27. თუ ოთხკუთხედის საპირისპირო კუთხეები წყვილებში ტოლია, მაშინ ის პარალელოგრამია.
მოდით ∠ A=∠ C და ∠ B=∠ D. რადგან ∠ A+∠ B+∠ C+∠ D=360 o, შემდეგ ∠ A+∠ B=180 o და AD და BC გვერდები პარალელურია (სწორი წრფეების პარალელიზმზე დაყრდნობით). ჩვენ ასევე დავამტკიცებთ AB და CD გვერდების პარალელიზმს და დავასკვნით, რომ ABCD განსაზღვრებით პარალელოგრამია.
თეორემა 28. თუ ოთხკუთხედის მიმდებარე კუთხეები, ე.ი. ერთი მხარის მიმდებარე კუთხეები ემატება 180 გრადუსს, მაშინ ის პარალელოგრამია.
თუ შიდა ცალმხრივი კუთხეები ემატება 180 გრადუსს, მაშინ სწორი ხაზები პარალელურია. ასე რომ, AB არის CD-ის პარალელურად, ხოლო BC არის AD-ის პარალელურად. ოთხკუთხედი გამოდის პარალელოგრამი განსაზღვრებით.
თეორემა 29. თუ ოთხკუთხედის დიაგონალები ერთმანეთს კვეთენ გადაკვეთის ადგილას, მაშინ ოთხკუთხედი პარალელოგრამია.
მტკიცებულება. თუ AO = OC, BO = OD, მაშინ სამკუთხედები AOD და BOC ტოლია, რადგან აქვთ ტოლი (ვერტიკალური) კუთხეები O წვეროზე, ჩასმული ტოლ გვერდებს შორის. სამკუთხედების ტოლობიდან ვასკვნით, რომ AD და BC ტოლია. გვერდები AB და CD ასევე ტოლია, ხოლო ოთხკუთხედი აღმოჩნდება პარალელოგრამი 1 კრიტერიუმის მიხედვით.
თეორემა 30. თუ ოთხკუთხედს აქვს წყვილი თანაბარი, პარალელური გვერდი, მაშინ ის პარალელოგრამია.
ABCD ოთხკუთხედის AB და CD გვერდები იყოს პარალელური და ტოლი. დავხატოთ AC და BD დიაგონალები. ამ წრფეების პარალელიზმიდან გამომდინარეობს, რომ განივი კუთხეები ABO = CDO და BAO = OCD ტოლია. სამკუთხედები ABO და CDO ტოლია გვერდით და მიმდებარე კუთხით. ამიტომ AO=OS, VO=ОD, ე.ი. დიაგონალები იყოფა შუაზე გადაკვეთის წერტილით და ოთხკუთხედი აღმოჩნდება პარალელოგრამი 4 კრიტერიუმის მიხედვით.

გეომეტრიაში განიხილება პარალელოგრამების განსაკუთრებული შემთხვევები.

ეს არის ოთხკუთხედი, რომლის მოპირდაპირე მხარეები პარალელურია წყვილებში.

საკუთრება 1. პარალელოგრამის ნებისმიერი დიაგონალი მას ორ ტოლ სამკუთხედად ყოფს.

მტკიცებულება . II მახასიათებლის მიხედვით (ჯვარედინი კუთხეები და საერთო მხარე).

თეორემა დადასტურებულია.

საკუთრება 2. პარალელოგრამში მოპირდაპირე გვერდები ტოლია და მოპირდაპირე კუთხეები ტოლია.

მტკიცებულება .
ანალოგიურად,

თეორემა დადასტურებულია.

თვისება 3. პარალელოგრამში დიაგონალები იკვეთება გადაკვეთის წერტილით.

მტკიცებულება .

თეორემა დადასტურებულია.

საკუთრება 4. პარალელოგრამის კუთხის ბისექტორი, რომელიც კვეთს მოპირდაპირე მხარეს, ყოფს მას ტოლფერდა სამკუთხედად და ტრაპეციად. (ჩ. სიტყვები - წვერო - ორი ტოლფერდა? -კა).

მტკიცებულება .

თეორემა დადასტურებულია.

საკუთრება 5. პარალელოგრამში წრფის სეგმენტი მოპირდაპირე მხარეს ბოლოებით, რომელიც გადის დიაგონალების გადაკვეთის წერტილში, ორად არის გაყოფილი ამ წერტილით.

მტკიცებულება .

თეორემა დადასტურებულია.

საკუთრება 6. პარალელოგრამის ბლაგვი კუთხის წვეროდან ჩამოშვებულ სიმაღლეებს შორის კუთხე უდრის პარალელოგრამის მახვილ კუთხეს.

მტკიცებულება .

თეორემა დადასტურებულია.

საკუთრება 7. ერთი მხარის მიმდებარე პარალელოგრამის კუთხეების ჯამი არის 180°.

მტკიცებულება .

თეორემა დადასტურებულია.

კუთხის ბისექტრის აგება. სამკუთხედის კუთხის ბისექტრის თვისებები.

1) ააშენეთ თვითნებური სხივი DE.

2) მოცემულ სხივზე ააგეთ თვითნებური წრე წვეროზე ცენტრით და იგივე
ცენტრით აშენებული სხივის დასაწყისში.

3) F და G - წრის გადაკვეთის წერტილები მოცემული კუთხის გვერდებთან, H - წრის გადაკვეთის წერტილი აგებულ სხივთან.

ააგეთ წრე H წერტილში ცენტრით და რადიუსით FG-ის ტოლი.

5) I არის აგებული სხივის წრეების გადაკვეთის წერტილი.

6) დახაზეთ სწორი ხაზი წვეროზე და I.

IDH არის საჭირო კუთხე.
)

საკუთრება 1. სამკუთხედის კუთხის ბისექტრი მოპირდაპირე მხარეს ყოფს მიმდებარე გვერდების პროპორციულად.

მტკიცებულება . მოდით x, y იყოს c გვერდის სეგმენტები. გავაგრძელოთ სხივი ძვ.წ. BC სხივზე C-დან გამოვსახავთ CK სეგმენტს AC-ის ტოლი.

პარალელოგრამი არის ოთხკუთხედი, რომლის მოპირდაპირე გვერდები პარალელურია წყვილებში.

ეს განმარტება უკვე საკმარისია, ვინაიდან პარალელოგრამის დარჩენილი თვისებები მისგან გამომდინარეობს და დადასტურებულია თეორემების სახით.

• პარალელოგრამის ძირითადი თვისებებია:
• პარალელოგრამი არის ამოზნექილი ოთხკუთხედი;
• პარალელოგრამს აქვს მოპირდაპირე გვერდები, რომლებიც ტოლია წყვილებში;
• პარალელოგრამში მოპირდაპირე კუთხეები წყვილებში ტოლია;

პარალელოგრამის დიაგონალები იყოფა შუაზე გადაკვეთის წერტილით.

პარალელოგრამი - ამოზნექილი ოთხკუთხედი ჯერ დავამტკიცოთ თეორემა, რომპარალელოგრამი არის ამოზნექილი ოთხკუთხედი

. მრავალკუთხედი ამოზნექილია, თუ მისი რომელი გვერდი სწორ ხაზამდეა გაშლილი, მრავალკუთხედის ყველა სხვა მხარე იქნება ამ სწორი ხაზის იმავე მხარეს.

მიეცით პარალელოგრამი ABCD, რომელშიც AB არის მოპირდაპირე მხარე CD-სთვის, ხოლო BC არის მოპირდაპირე მხარე AD-სთვის. შემდეგ პარალელოგრამის განმარტებიდან გამომდინარეობს, რომ AB || CD, BC || ახ.წ.

პარალელურ სეგმენტებს არ აქვთ საერთო წერტილები და არ იკვეთებიან. ეს ნიშნავს, რომ CD დევს AB-ის ერთ მხარეს. ვინაიდან BC სეგმენტი აკავშირებს AB სეგმენტის B წერტილს CD სეგმენტის C წერტილთან, ხოლო AD სეგმენტი აკავშირებს სხვა AB და CD წერტილებს, BC და AD სეგმენტები ასევე დევს AB ხაზის იმავე მხარეს, სადაც დევს CD. ამრიგად, სამივე მხარე - CD, BC, AD - AB-ის ერთ მხარეს დევს.

ანალოგიურად, დადასტურდა, რომ პარალელოგრამის სხვა გვერდებთან მიმართებაში, დანარჩენი სამი მხარე ერთ მხარეს დევს.

მოპირდაპირე მხარეები და კუთხეები ტოლია პარალელოგრამის ერთ-ერთი თვისებაა ისპარალელოგრამში მოპირდაპირე გვერდები და მოპირდაპირე კუთხეები წყვილებში ტოლია

. მაგალითად, თუ პარალელოგრამი მოცემულია ABCD, მაშინ მას აქვს AB = CD, AD = BC, ∠A = ∠C, ∠B = ∠D. ეს თეორემა დადასტურებულია შემდეგნაირად.

ამ სამკუთხედებს ერთი გვერდი აქვთ საერთო - AC. კუთხე BCA უდრის CAD კუთხეს, ისევე როგორც ვერტიკალური, როდესაც BC და AD პარალელურია. კუთხეები BAC და ACD ასევე ტოლია ვერტიკალური კუთხეების, როდესაც AB და CD პარალელურია. ამიტომ, ∆ABC = ∆ADC ორ კუთხით და მათ შორის მდებარე გვერდით.

ამ სამკუთხედებში AB გვერდი შეესაბამება CD მხარეს, ხოლო BC გვერდი შეესაბამება AD. ამიტომ, AB = CD და BC = AD.

კუთხე B შეესაბამება D კუთხეს, ანუ ∠B = ∠D. პარალელოგრამის A კუთხე არის ორი კუთხის ჯამი - ∠BAC და ∠CAD. კუთხე C უდრის ∠BCA და ∠ACD. ვინაიდან კუთხეების წყვილი ერთმანეთის ტოლია, მაშინ ∠A = ∠C.

ამრიგად, დადასტურებულია, რომ პარალელოგრამში მოპირდაპირე გვერდები და კუთხეები ტოლია.

დიაგონალები იყოფა ნახევრად

ვინაიდან პარალელოგრამი არის ამოზნექილი ოთხკუთხედი, მას აქვს ორი დიაგონალი და ისინი იკვეთებიან. მოცემული იყოს ABCD პარალელოგრამი, მისი დიაგონალები AC და BD იკვეთება E წერტილში. განვიხილოთ მათ მიერ წარმოქმნილი სამკუთხედები ABE და CDE.

ამ სამკუთხედებს აქვთ AB და CD გვერდები პარალელოგრამის მოპირდაპირე გვერდების ტოლი. ABE კუთხე უდრის CDE კუთხს, როგორც ჯვარედინი მდგომი პარალელური წრფეებით AB და CD. ამავე მიზეზით, ∠BAE = ∠DCE. ეს ნიშნავს ∆ABE = ∆CDE ორ კუთხით და მათ შორის არსებულ მხარეს.

თქვენ ასევე შეგიძლიათ შეამჩნიოთ, რომ კუთხეები AEB და CED ვერტიკალურია და, შესაბამისად, ერთმანეთის ტოლია.

ვინაიდან სამკუთხედები ABE და CDE ერთმანეთის ტოლია, მაშინ მათი ყველა შესაბამისი ელემენტი ტოლია. პირველი სამკუთხედის AE გვერდი შეესაბამება მეორის CE მხარეს, რაც ნიშნავს AE = CE. ანალოგიურად BE = DE. თანაბარი სეგმენტების თითოეული წყვილი წარმოადგენს პარალელოგრამის დიაგონალს. ამრიგად, დადასტურებულია, რომ პარალელოგრამის დიაგონალები იკვეთება მათი გადაკვეთის წერტილით.

პარალელოგრამის კონცეფცია

განმარტება 1

პარალელოგრამიარის ოთხკუთხედი, რომელშიც მოპირდაპირე გვერდები ერთმანეთის პარალელურია (ნახ. 1).

სურათი 1.

პარალელოგრამს ორი ძირითადი თვისება აქვს. განვიხილოთ ისინი მტკიცებულების გარეშე.

საკუთრება 1: პარალელოგრამის საპირისპირო გვერდები და კუთხეები, შესაბამისად, ტოლია.

საკუთრება 2: პარალელოგრამზე დახატული დიაგონალები იკვეთება მათი გადაკვეთის წერტილით.

პარალელოგრამის ნიშნები

განვიხილოთ პარალელოგრამის სამი მახასიათებელი და წარმოვადგინოთ ისინი თეორემების სახით.

თეორემა 1

თუ ოთხკუთხედის ორი გვერდი ერთმანეთის ტოლია და ასევე პარალელურია, მაშინ ეს ოთხკუთხედი პარალელოგრამი იქნება.

მტკიცებულება.

მოდით, მოგვცეს ოთხკუთხედი $ABCD$. რომელშიც $AB||CD$ და $AB=CD$ მოდით დავხატოთ მასში $AC$ დიაგონალი (ნახ. 2).

სურათი 2.

განვიხილოთ პარალელური ხაზები $AB$ და $CD$ და მათი სეკანტი $AC$. მერე

\[\კუთხე CAB=\კუთხე DCA\]

როგორც გადაჯვარედინებული კუთხეები.

სამკუთხედების ტოლობის $I$ კრიტერიუმის მიხედვით,

ვინაიდან $AC$ მათი საერთო მხარეა და $AB=CD$ პირობით. ნიშნავს

\[\კუთხე DAC=\კუთხე ACB\]

განვიხილოთ $AD$ და $CB$ წრფეები და მათი სკანტი $AC$ ბოლო ტოლობის მიხედვით, ჩვენ ვიღებთ $AD||CB$.) შესაბამისად, $1$, ეს ოთხკუთხედი არის პარალელოგრამი.

თეორემა დადასტურდა.

თეორემა 2

თუ ოთხკუთხედის საპირისპირო გვერდები ერთმანეთის ტოლია, მაშინ ის პარალელოგრამია.

მტკიცებულება.

მოდით, მოგვცეს ოთხკუთხედი $ABCD$. რომელშიც $AD=BC$ და $AB=CD$. დავხატოთ მასში $AC$ დიაგონალი (ნახ. 3).

სურათი 3.

ვინაიდან $AD=BC$, $AB=CD$ და $AC$ არის საერთო გვერდი, მაშინ სამკუთხედების ტოლობის $III$ კრიტერიუმით,

\[\სამკუთხედი DAC=\სამკუთხედი ACB\]

\[\კუთხე DAC=\კუთხე ACB\]

მოდით განვიხილოთ $AD$ და $CB$ წრფეები და მათი სეკანტი $AC$ ბოლო ტოლობის მიხედვით, ჩვენ მივიღებთ $AD||CB$-ს. ამიტომ, განსაზღვრებით $1$, ეს ოთხკუთხედი არის პარალელოგრამი.

\[\კუთხე DCA=\კუთხე CAB\]

განვიხილოთ $AB$ და $CD$ წრფეები და მათი სეკანტი $AC$ ტყუილის კუთხით ბოლო ტოლობით მივიღებთ $AB||CD$; ამიტომ, განმარტებით 1, ეს ოთხკუთხედი არის პარალელოგრამი.

თეორემა დადასტურდა.

თეორემა 3

თუ ოთხკუთხედში დახატული დიაგონალები მათი გადაკვეთის წერტილით იყოფა ორ ტოლ ნაწილად, მაშინ ეს ოთხკუთხედი პარალელოგრამია.

მტკიცებულება.

მოდით, მოგვცეს ოთხკუთხედი $ABCD$. მოდით დავხატოთ მასში $AC$ და $BD$ დიაგონალები. მოდით, ისინი გადაიკვეთონ $O$ წერტილში (ნახ. 4).

სურათი 4.

ვინაიდან, პირობით, $BO=OD,\ AO=OC$ და კუთხეები $\კუთხე COB=\კუთხე DOA$ ვერტიკალურია, მაშინ სამკუთხედების ტოლობის $I$ კრიტერიუმით,

\[\სამკუთხედი BOC=\სამკუთხედი AOD\]

\[\კუთხე DBC=\კუთხე BDA\]

განვიხილოთ წრფეები $BC$ და $AD$ და მათი სეკანტი $BD$ ბოლო ტოლობის მიხედვით ცრუ კუთხით მივიღებთ $BC||AD$; ასევე $BC=AD$. მაშასადამე, $1$ თეორემის მიხედვით, ეს ოთხკუთხედი არის პარალელოგრამი.

ვიდეოკურსი „მიიღე A“ მოიცავს ყველა იმ თემას, რომელიც აუცილებელია მათემატიკაში ერთიანი სახელმწიფო გამოცდის წარმატებით ჩაბარებისთვის 60-65 ქულით. მათემატიკაში პროფილის ერთიანი სახელმწიფო გამოცდის ყველა დავალება 1-13 სრულად. ასევე შესაფერისია მათემატიკაში ძირითადი ერთიანი სახელმწიფო გამოცდის ჩასაბარებლად. თუ გსურთ ერთიანი სახელმწიფო გამოცდის ჩაბარება 90-100 ქულით, პირველი ნაწილი 30 წუთში და უშეცდომოდ უნდა მოაგვაროთ!

ერთიანი სახელმწიფო გამოცდისთვის მოსამზადებელი კურსი 10-11 კლასებისთვის, ასევე მასწავლებლებისთვის. ყველაფერი, რაც გჭირდებათ მათემატიკაში ერთიანი სახელმწიფო გამოცდის 1 ნაწილის (პირველი 12 ამოცანის) და მე-13 ამოცანის (ტრიგონომეტრია) გადასაჭრელად. ეს კი ერთიან სახელმწიფო გამოცდაზე 70 ქულაზე მეტია და მათ გარეშე ვერც 100-ქულიანია და ვერც ჰუმანიტარული მეცნიერება.

ყველა საჭირო თეორია. ერთიანი სახელმწიფო გამოცდის სწრაფი გადაწყვეტილებები, ხარვეზები და საიდუმლოებები. გაანალიზებულია FIPI Task Bank-ის პირველი ნაწილის ყველა მიმდინარე დავალება. კურსი სრულად შეესაბამება 2018 წლის ერთიანი სახელმწიფო გამოცდის მოთხოვნებს.

კურსი შეიცავს 5 დიდ თემას, თითო 2,5 საათი. თითოეული თემა მოცემულია ნულიდან, მარტივად და ნათლად.

ასობით ერთიანი სახელმწიფო გამოცდის დავალება. სიტყვის პრობლემები და ალბათობის თეორია. მარტივი და ადვილად დასამახსოვრებელი ალგორითმები პრობლემების გადასაჭრელად. გეომეტრია. თეორია, საცნობარო მასალა, ყველა სახის ერთიანი სახელმწიფო საგამოცდო ამოცანების ანალიზი. სტერეომეტრია. რთული გადაწყვეტილებები, სასარგებლო მოტყუების ფურცლები, სივრცითი წარმოსახვის განვითარება. ტრიგონომეტრია ნულიდან ამოცანამდე 13. გაგება ჩაკეტვის ნაცვლად. რთული ცნებების მკაფიო ახსნა. ალგებრა. ფესვები, სიმძლავრეები და ლოგარითმები, ფუნქცია და წარმოებული. ერთიანი სახელმწიფო გამოცდის მე-2 ნაწილის რთული ამოცანების გადაჭრის საფუძველი.